Snub 24-cell: Difference between revisions
Double sharp (talk | contribs) |
Tags: Mobile edit Mobile web edit |
||
| Line 71: | Line 71: | ||
{| class=wikitable |
{| class=wikitable |
||
|+ Orthogonal projection, F<sub>4</sub> |
|+ Orthogonal projection, F<sub>4</sub> Coxeter plane |
||
!Snub 24-cell |
!Snub 24-cell |
||
!600-cell |
!600-cell |
||
Revision as of 11:57, 11 February 2015
| Snub 24-cell | ||
 Orthogonal projection Centered on hyperplane of one icosahedron. | ||
| Type | Uniform 4-polytope | |
| Schläfli symbol[1] | s{3,4,3} sr{3,3,4} s{31,1,1} | |
| Coxeter-Dynkin diagrams |
| |
| Cells | 144 | 96 3.3.3 (oblique) 24 3.3.3 24 3.3.3.3.3 |
| Faces | 480 {3} | |
| Edges | 432 | |
| Vertices | 96 | |
| Vertex figure |  (Tridiminished icosahedron) | |
| Symmetry groups | [3+,4,3], ½F4, order 576
[(3,3)+,4], ½BC4, order 192 | |
| Properties | convex | |
| Uniform index | 30 31 32 | |

8 faces:


5 3.3.3 and 3 3.3.3.3.3
In geometry, the snub 24-cell or snub disicositetrachoron is a convex uniform 4-polytope composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices.
Semiregular polytope
It is one of three semiregular 4-polytopes made of two or more cells which are Platonic solids, discovered by Thorold Gosset in his 1900 paper. He called it a tetricosahedric for being made of tetrahedron and icosahedron cells. (The other two are the rectified 5-cell and rectified 600-cell.)
Alternative names
- Snub icositetrachoron
- Snub demitesseract
- Semi-snub polyoctahedron (John Conway)[2]
- Sadi (Jonathan Bowers: for snub disicositetrachoron)
- Tetricosahedric Thorold Gosset, 1900[3]
Geometry
The snub 24-cell is related to the truncated 24-cell by an alternation operation. Half the vertices are deleted, the 24 truncated octahedron cells become 24 icosahedron cells, the 24 cubes become 24 tetrahedron cells, and the 96 deleted vertex voids create 96 new tetrahedron cells.
 A net of the snub 24-cell with blue icosahedra, and red and yellow tetrahedra. |
The snub 24-cell may also be constructed by a particular diminishing of the 600-cell: by removing 24 vertices from the 600-cell corresponding to those of an inscribed 24-cell, and then taking the convex hull of the remaining vertices. This is equivalent to removing 24 icosahedral pyramids from the 600-cell.
| Snub 24-cell | 600-cell |
|---|---|

|

|
Coordinates
The vertices of a snub 24-cell centered at the origin of 4-space, with edges of length 2, are obtained by taking even permutations of
- (0, ±1, ±φ, ±φ2)
(where φ = (1+√5)/2 is the golden ratio).
These 96 vertices can be found by partitioning each of the 96 edges of a 24-cell into the golden ratio in a consistent manner, in much the same way that the 12 vertices of an icosahedron or "snub octahedron" can be produced by partitioning the 12 edges of an octahedron in the golden ratio. This is done by first placing vectors along the 24-cell's edges such that each two-dimensional face is bounded by a cycle, then similarly partitioning each edge into the golden ratio along the direction of its vector.[4] The 96 vertices of the snub 24-cell, together with the 24 vertices of a 24-cell, form the 120 vertices of the 600-cell.
Structure
Each icosahedral cell is joined to 8 other icosahedral cells at 8 triangular faces in the positions corresponding to an inscribing octahedron. The remaining triangular faces are joined to tetrahedral cells, which occur in pairs that share an edge on the icosahedral cell.
The tetrahedral cells may be divided into two groups, of 96 cells and 24 cells respectively. Each tetrahedral cell in the first group is joined via its triangular faces to 3 icosahedral cells and one tetrahedral cell in the second group, while each tetrahedral cell in the second group is joined to 4 tetrahedra in the first group.
Symmetry
The snub 24-cell has three vertex-transitive colorings based on a Wythoff construction on a Coxeter group from which it is alternated: F4 defines 24 interchangeable icosahedra, while the BC4 group defines two groups of icosahedra in a 8:16 counts, and finally the D4 group has 3 groups of icosahedra with 8:8:8 counts.
| Symmetry (order) |
Constructive name | Coxeter-Dynkin diagram Extended Schläfli symbol |
Vertex figure (Tridiminished icosahedron) |
Cells (Colored as faces in vertex figures) |
|---|---|---|---|---|
| ½F4 [3+,4,3] (576) |
Snub 24-cell | s{3,4,3} |
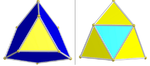
|
One set of 24 icosahedra (blue) Two sets of tetrahedra: 96 (yellow) and 24 (cyan) |
| ½BC4 [(3,3)+,4] (192) |
Snub rectified 16-cell | sr{3,3,4} |

|
Two sets icosahedra: 8, 16 each (red and blue) Two sets of tetrahedra: 96 (yellow) and 24 (cyan) |
| ½D4 [31,1,1]+ (96) |
Snub demitesseract | s{31,1,1} |

|
Three sets of 8 icosahedra (red, green, and blue) Two sets of tetrahedra: 96 (yellow) and 24 (cyan) |
Conversely, the 600-cell may be constructed from the snub 24-cell by augmenting it with 24 icosahedral pyramids.
Projections
Orthographic projections
| Coxeter plane | F4 | B4 |
|---|---|---|
| Graph | 
|

|
| Dihedral symmetry | [12]+ | [8/2] |
| Coxeter plane | D4 / B3 / A2 | B2 / A3 |
| Graph | 
|

|
| Dihedral symmetry | [6]+ | [4] |
Perspective projections
| Perspective projections | |
|---|---|
 Perspective projection centered on an icosahedral cell, with 4D viewpoint placed at a distance of 5 times the vertex-center radius. The nearest icosahedral cell is rendered in solid color, and the other cells are in edge-outline. Cells facing away from the 4D viewpoint are culled, to reduce visual clutter. |
 The same projection, now with 4 of the 8 icosahedral cells surrounding the central cell shown in green. |
 The same projection as above, now with the other 4 icosahedral cells surrounding the central cell shown in magenta. The animated version of this image gives a good view on the layout of these cells. From this particular viewpoint, one of the gaps containing tetrahedral cells can be seen. Each of these gaps are filled by 5 tetrahedral cells, not shown here. |
 Same projection as above, now with the central tetrahedral cell in the gap filled in. This tetrahedral cell is joined to 4 other tetrahedral cells, two of which fills the two gaps visible in this image. The other two each lies between a green tetrahedral cell, a magenta cell, and the central cell, to the left and right of the yellow tetrahedral cell. Note that in these images, cells facing away from the 4D viewpoint have been culled; hence there are only a total of 1 + 8 + 6 + 24 = 39 cells accounted for here. The other cells lie on the other side of the snub 24-cell. Part of the edge outline of one of them, an icosahedral cell, can be discerned here, overlying the yellow tetrahedron. |
 In this image, only the nearest icosahedral cell and the 6 yellow tetrahedral cells from the previous image are shown. |
 Now the 12 tetrahedral cells joined to the central icosahedral cell and the 6 yellow tetrahedral cells are shown. Each of these cells is surrounded by the central icosahedron and two of the other icosahedral cells shown earlier. |
 Finally, the other 12 tetrahedral cells joined to the 6 yellow tetrahedral cells are shown here. These cells, together with the 8 icosahedral cells shown earlier, comprise all the cells that share at least 1 vertex with the central cell. | |
Related polytopes
| D4 uniform polychora | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

| ||||
| {3,31,1} h{4,3,3} |
2r{3,31,1} h3{4,3,3} |
t{3,31,1} h2{4,3,3} |
2t{3,31,1} h2,3{4,3,3} |
r{3,31,1} {31,1,1}={3,4,3} |
rr{3,31,1} r{31,1,1}=r{3,4,3} |
tr{3,31,1} t{31,1,1}=t{3,4,3} |
sr{3,31,1} s{31,1,1}=s{3,4,3} | ||||
The snub 24-cell is also called a semi-snub 24-cell because it is not a true snub (alternation of an omnitruncated 24-cell). The full snub 24-cell can also be constructed although it is not uniform, being composed of irregular tetrahedra on the alternated vertices.
The snub 24-cell is the largest facet of the 4-dimensional honeycomb, the snub 24-cell honeycomb.
The snub 24-cell is a part of the F4 symmetry family of uniform 4-polytopes.
| 24-cell family polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | 24-cell | truncated 24-cell | snub 24-cell | rectified 24-cell | cantellated 24-cell | bitruncated 24-cell | cantitruncated 24-cell | runcinated 24-cell | runcitruncated 24-cell | omnitruncated 24-cell | |
| Schläfli symbol |
{3,4,3} | t0,1{3,4,3} t{3,4,3} |
s{3,4,3} | t1{3,4,3} r{3,4,3} |
t0,2{3,4,3} rr{3,4,3} |
t1,2{3,4,3} 2t{3,4,3} |
t0,1,2{3,4,3} tr{3,4,3} |
t0,3{3,4,3} | t0,1,3{3,4,3} | t0,1,2,3{3,4,3} | |
| Coxeter diagram |
|||||||||||
| Schlegel diagram |

|

|

|

|

|

|

|

|

|

| |
| F4 | 
|

|

|

|

|

|

|

|

|

| |
| B4 | 
|

|

|

|

|

|

|

|

|

| |
| B3(a) | 
|

|

|

|

|

|

|

|

|

| |
| B3(b) | 
|

|

|

|

|

| |||||
| B2 | 
|

|

|

|

|

|

|

|

|

| |
See also
Notes
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- H. S. M. Coxeter (1973). Regular Polytopes. New York: Dover Publications Inc. pp. 151–152, 156–157.
- Snub icositetrachoron - Data and images
- 3. Convex uniform polychora based on the icositetrachoron (24-cell) - Model 31, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora) s3s4o3o - sadi".
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
- Snub 24-Cell Derived from the Coxeter-Weyl Group W(D4) [1], Mehmet Koca, Nazife Ozdes Koca, Muataz Al-Barwani (2012);Int. J. Geom. Methods Mod. Phys. 09, 1250068 (2012)
External links
- Print #11: Snub icositetrachoron net, George Olshevsky.
