Diamond cut: Difference between revisions

Content deleted Content added

Inline

Revision as of 01:48, 25 July 2006

This article addresses the many styles of diamond cut. For a broader discussion of diamonds, see diamond. For other uses of the word diamond, see diamond (disambiguation).

In order to best utilize a diamond gemstone's superlative material properties, a number of different diamond cuts have been developed. A diamond cut constitutes a more or less symmetrical arrangement of facets which together modify the shape and appearance of a diamond crystal. Diamond cutters must consider several factors, such as the shape and size of the crystal, when choosing a cut. The practical history of diamond cuts can be traced back to the Middle Ages, while their theoretical basis was not developed until the turn of the 20th century. Design creation and innovation continue to the present day: new technology—notably laser cutting and computer-aided design—has enabled the development of cuts whose complexity, optical performance, and waste reduction were hitherto unthinkable.

The most popular of diamond cuts is the modern round brilliant, whose facet arrangements and proportions have been perfected by both mathematical and empirical analysis. Also popular are the fancy cuts which come in a variety of shapes—many of which were derived from the round brilliant. A diamond's cut is evaluated by trained graders, with higher grades given to stones whose symmetry and proportions most closely match the particular "ideal" used as a benchmark. The strictest standards are applied to the round brilliant; although its facet count is invariable, its proportions are not. Different countries base their cut grading on different ideals: one may speak of the American Standard or the Scandinavian Standard (Scan. D.N.), to give but two examples.

History

The history of diamond cuts can be traced to the late Middle Ages, before which time diamonds were enjoyed in their natural octahedral state—anhedral (poorly formed) diamonds simply were not used in jewellery. The first "improvements" on nature's design involved a simple polishing of the octahedral crystal faces to create even and unblemished facets, or to fashion the desired octahedral shape out of an otherwise unappealing piece of rough. This was called the point cut and dates from the mid 14th century; by 1375 there was a guild of diamond polishers at Nürnberg. By the mid 15th century, the point cut began to be improved upon: a little less than one half of the octahedron would be sawn off, creating the table cut. The importance of a culet was also realised, and some table-cut stones may possess one. The addition of four corner facets created the old single cut (or old eight cut). Neither of these early cuts would reveal what diamond is prized for today; its strong dispersion or fire. At the time, diamond was valued chiefly for its adamantine lustre and superlative hardness; a table-cut diamond would appear black to the eye, as they do in paintings of the era. For this reason, colored gemstones such as ruby and sapphire were far more popular in jewelry of the era.

In or around 1476 Lodewyk (Louis) van Berquem, a Flemish polisher of Bruges, introduced absolute symmetry in the disposition of facets. He cut stones in the shape known as pendeloque or briolette; these were pear-shaped with triangular facets on both sides. About the middle of the 16th century, the rose or rosette was introduced in Antwerp: it also consisted of triangular facets arranged in a symmetrical radiating pattern, but with the bottom of the stone left flat—essentially a crown without a pavilion. Many large, famous Indian diamonds of old (such as the Orloff and Sancy) also feature a rose-like cut; there is some suggestion that Western cutters were influenced by Indian stones, because some of these diamonds may predate the Western adoption of the rose cut. However, Indian "rose cuts" were far less symmetrical as their cutters had the primary interest of conserving carat weight, due to the divine status of diamond in India. In either event, the rose cut continued to evolve, with its depth, number and arrangements of facets being tweaked.

The first brilliant cuts were introduced in the middle of the 17th century. Known as Mazarins, they had 17 facets on the crown (upper half). They are also called double-cut brilliants as they are seen as a step up from old single cuts. Vincent Peruzzi, a Venetian polisher, later increased the number of crown facets from 17 to 33 (triple-cut or Peruzzi brilliants), thereby significantly increasing the fire and brilliance of the cut gem, properties which in the Mazarin were already incomparably better than in the rose. Yet Peruzzi-cut diamonds, when seen nowadays, seem exceedingly dull compared to modern-cut brilliants. Because the practice of bruting (see diamond cutting) had not yet been developed, these early brilliants were all rounded squares or rectangles in cross-section (rather than circular). Given the general name of cushion—what are known today as old mine cuts—these were common by the early 18th century. Sometime later the old European cut was developed, which had a shallower pavilion, more rounded shape, and different arrangement of facets. The old European cut was the forerunner of modern brilliants and was the most advanced in use during the 19th century.

Around 1900, the development of diamond saws and good jewelry lathes enabled the development of modern diamond cutting and diamond cuts, chief among them the round brilliant cut. In 1919, Marcel Tolkowsky analyzed this cut: his calculations took both brilliance (the amount of white light reflected) and fire into consideration, creating a delicate balance between the two. His geometric calculations can be found in his book on Diamond Design[1]. Tolkowsky's calculations would serve as the basis for all future brilliant cut modifications and standards.

These days many people have over used Tolkowsky's "ideal" model. The original model were general guidelines as there were several aspects of diamond cut that was not explored or accounted for in the original model. Excerpts from GIA article What did Marcel Tolkowsky really say?:

"Because every facet has the potential to change a light ray's plane of travel, every facet must be considered in any complete calculation of light paths. Just as a two-dimensional slice of a diamond provides incomplete information about the three-dimensional nature of light behavior inside a diamond, this two-dimensional slice also provides incomplete information about light behavior outside the diamond. A diamond's panorama is three-dimensional. Although diamonds are highly symmetrical, light can enter a diamond from many directions and many angles. This factor further highlights the need to reevaluate Tolkowsky's results, and to recalculate the effects of a diamond's proportions on its appearance aspects.

Another important point to consider is that Tolkowsky did not follow the path of a ray that was reflected more than twice in the diamond. However, we now know that a diamond's appearance is composed of many light paths that reflect considerably more than two times within that diamond. Once again, we can see that Tolkowsky's predictions are helpful in explaining optimal diamond performance, but they are incomplete by today's technological standards." Even Tolkowsky's guidelines should be carefully used of only as guidlines as opposed to a definitive answer for determining the proportions of a round brilliant cut diamond.

In the 1970s, Bruce Harding developed another mathematical model for gem design. Since then, several groups have used computer models (e.g., MSU, OctoNus, GIA, and folds.net) and specialized scopes to design diamond cuts.

The world´s top diamond cutting and polishing center is India. It processes 11 out of 12 diamonds in jewellery worldwide. The sector employs 1.3 million people and accounts for 14 percent of India's $80 billion of annual exports. Its share in the world polished diamond market is 92 percent by pieces and 55 percent by value.

Theory

In its rough state, a diamond is fairly unremarkable in appearance. Most gem diamonds are recovered from secondary or alluvial deposits, and such diamonds have dull, battered external surfaces often covered by a gummy, opaque skin—a comparison to "lumps of washing soda" is apt. The act of polishing a diamond and creating flat facets in symmetrical arrangement brings out the diamond's hidden beauty in dramatic fashion.

When designing a diamond cut, two primary factors are considered. Foremost is the refractive index (RI) of diamond, which is fairly high compared to most other gems, at 2.417 (as measured by sodium light, 589.3 nm). Diamond's RI is responsible for its brilliance—the amount of incident light reflected back to the viewer. Also important is diamond's dispersive power—the ability of the material to split white light into its component spectral colors—which is also relatively high, at 0.044 (as measured from the B-G interval). The flashes of spectral colors—known as fire—are a function of this dispersion, but is, like brilliance, only apparent after cutting.

Brilliance can be divided into the definitions external brilliance and internal brilliance. The former is the light reflected from the surface of the stone—its luster. Diamond's adamantine ("diamond-like") luster is second only to metallic (i.e., that of metals); while it is directly related to RI, the quality of a finished stone's polish will determine how well a diamond's luster is borne out.

Internal brilliance—the percentage of incident light reflected back to the viewer from the rear (pavilion) facets—relies on careful consideration of a cut's interfacial angles as they relate to diamond's RI. The goal is to attain total internal reflection (TIR) by choosing the crown angle and pavilion angle (the angle formed by the pavilion facets and girdle plane) such the reflected light's angle of incidence (when reaching the pavilion facets) falls outside diamond's critical angle, or minimum angle for TIR, of 24.4°. Two observations can be made: if the pavilion is too shallow, light meets the pavilion facets within the critical angle, and is refracted (i.e., lost) through the pavilion bottom into the air. If the pavilion is too deep, light is initially reflected outside the critical angle on one side of the pavilion, but meets the opposite side within the critical angle and is then refracted out the side of the stone.

The term scintillation brilliance is applied to the number and arrangement of light reflections from the internal facets; that is, the degree of "sparkle" seen when the stone or observer moves. Scintillation is dependent on the size, number, and symmetry of facets, as well as on quality of polish. Very small stones will appear milky if their scintillation is too great (due to the limitations of the human eye), whereas larger stones will appear lifeless if their facets are too large or too few.

A diamond's fire is determined by the cut's crown height and crown angle (the crown being the top half of the stone, above the girdle), and the size and number of facets that compose it. The crown acts as a prism: light exiting the stone (after reflection from the pavilion facets) should meet the crown facets at as great an angle of incidence from the normal as possible (without exceeding the critical angle) in order to achieve the greatest fanning out or spread of spectral colors. The crown height is related to the crown angle, the crown facet size, and the table size (the largest central facet of the crown): a happy medium is sought in a table that is not too small (which would result in larger crown facets and greater fire at the expense of brilliance) or too large (which would result in smaller crown facets and little to no fire).

Choice of cut

The choice of diamond cut is often decided by the original shape of the rough stone, location of internal flaws or inclusions, the preservation of carat weight, and popularity of certain shapes amongst consumers. The cutter must consider each of these variables before proceeding.

Most gem-quality diamond crystals are octahedrons in their rough state (see material properties of diamond). These crystals are usually cut into round brilliants because it is possible to cut two such stones out of one octahedron with minimal loss of weight. If the crystal is malformed or twinned, or if inclusions are present at inopportune locations, the diamond is more likely to receive a fancy cut (a cut other than a round brilliant). This is especially true in the case of macles, which are flattened twin octahedron crystals. Round brilliants have certain requisite proportions which would result in high weight loss, whereas fancy cuts are typically much more flexible in this regard. Sometimes the cutters compromise and accept lesser proportions and symmetry in order to avoid inclusions or to preserve carat weight, since the per-carat price of diamond is much higher when the stone is over one carat (200 mg).

While the round brilliant cut is considered standard for diamond, with its shape and proportions nearly constant, the choice of fancy cut is influenced heavily by fashion. For example, the step cut baguette—which accentuates a diamond's luster, whiteness, and clarity but downplays its fire—was all the rage during the Art Deco period, whereas the mixed Princess cut—which accentuates a diamond's fire and brilliance rather than its luster—is currently gaining popularity. The princess cut is also popular amongst diamond cutters: of all the cuts, it wastes the least of the original crystal. Older diamonds cut before ca. 1900 were cut in "primitive" versions of the modern round brilliant, such as the rose cut and old mine cut (see History section). Although there is a market for antique stones, many are recut into modern brilliants to increase their marketability. There is also increasing demand for diamonds to be cut in older styles for the purpose of repairing or reproducing antique jewelry.

The size of a diamond may also be a factor. Very small (< 0.02 carats) diamonds—known as melée—are usually given simplified cuts (i.e., with fewer facets). This is because a full-cut brilliant of such small size would appear milky to the human eye, owing to its inability to resolve the stone's dispersive fire. Conversely, very large diamonds are usually given fancy cuts with many extra facets. Conventional round brilliant or fancy cuts do not scale up satisfactorily, so the extra facets are needed to ensure there are no "dead spots". Because large diamonds are less likely to be set in jewelry, their cuts are considered for how well they display the diamonds' properties from a wide range of viewing directions; in the case of more moderate-sized diamonds, the cuts are considered primarily for their face-up appeal.

Round brilliant

Developed ca. 1900, the round brilliant is the most popular cut given to diamond. It is usually the best choice in terms of saleability, insurability (due to its relatively "safe" shape), and desired optics.

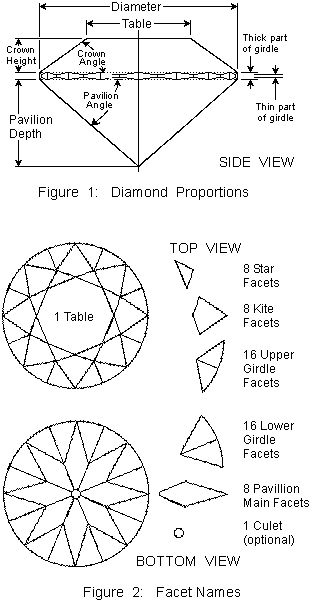
The modern round brilliant (Figure 1 and 2) consists of 58 facets (or 57 if the culet is excluded); 33 on the crown (the top half above the middle or girdle of the stone) and 25 on the pavilion (the lower half below the girdle). The girdle may be frosted, polished smooth, or faceted. In recent decades, most girdles are faceted; many have 32, 64, 80, or 96 facets (People's Diamonds has a distinctive 100 facet cut; these facets are excluded from the total facet count. Likewise, some diamonds may have a number of small extra facets on the crown or pavilion that were created to remove surface imperfections during the diamond cutting process. Depending on their size and location, they may negatively impact the symmetry of the cut and are therefore considered during cut grading.

Figure 1 assumes that the "thick part of the girdle" is the same thickness at all 16 "thick parts". It does not consider the effects of indexed upper girdle facets. Figure 2 is adapted from Figure 37 of Marcel Tolkowsky's Diamond Design, which was originally published in 1919. Since 1919, the lower girdle facets have become longer. As a result, the pavilion main facets have become narrower.

Proportions

While the facet count is standard, the actual proportions—crown height and crown angle, pavilion depth and pavilion angle, and table size—are not universally agreed upon. There are at least six "ideal cuts" that have been devised over the years, but only three are in common use as a means of benchmarking. Developed by Marcel Tolkowsky in 1919, the American Standard (also known as the American Ideal and Tolkowsky Brilliant) is the benchmark in North America. It was derived from mathematical calculations that considered both brilliance and fire. The benchmark in Germany and other European countries is the Practical Fine Cut (German: Feinschliff der Praxis, also known as the Eppler Cut), introduced in 1939. It was developed in Germany by empirical observations and differs only slightly from the American Standard. Introduced as part of the Scandinavian Diamond Nomenclature (Scan. D. N.) in 1969, the Scandinavian Standard also differs very little.

Other benchmarks include: the Ideal Brilliant (developed in 1929 by Johnson and Roesch); the Parker Brilliant (1951); and the Eulitz Brilliant (1972). The Ideal and Parker brilliants are disused because their proportions result in (by contemporary standards) an unacceptably low brilliance. The Eulitz cut is the only other mathematically-derived benchmark; it is also the only benchmark to consider girdle thickness. A summary of the different benchmarks is given below:

Benchmark	Crown height	Pavilion depth	Table diameter	Girdle thickness	Crown angle	Pavilion angle
American Standard	16.2%	43.1%	53.0%	N/A	34.5°	40.75°
Practical Fine Cut	14.4%	43.2%	56.0%	N/A	33.2°	40.8°
Scandinavian Standard	14.6%	43.1%	57.5%	N/A	34.5°	40.75°
Eulitz Brilliant	14.45%	43.15%	56.5%	1.5%	33.36°	40.48°
Ideal Brilliant	19.2%	40.0%	56.1%	N/A	41.1°	38.7°
Parker Brilliant	10.5%	43.4%	55.9%	N/A	25.5°	40.9°

Crown height, pavilion depth, and table diameter are percentages of the total girdle diameter. Because the pavilion angle (and consequently pavilion depth) is so closely tied to total internal reflection, it varies the least between the different standards.

Fancy cuts

Even with modern techniques, the cutting and polishing of a diamond crystal always results in a dramatic loss of weight; rarely is it less than 50 percent. The round brilliant cut is preferred when the crystal is an octahedron, as often two stones may be cut from one such crystal. Oddly shaped crystals such as macles are more likely to be cut in a fancy cut—that is, a cut other than the round brilliant—which the particular crystal shape lends itself to. The prevalence and choice of a particular fancy cut is also influenced by fashion; generally speaking, these cuts are not held to the same strict standards as Tolkowsky-derived round brilliants. Most fancy cuts can be grouped into four categories: modified brilliants, step cuts, mixed cuts, and rose cuts.

Modified brilliants

This is the most populous category of fancy cut, because the standard round brilliant can be effectively modified into a wide range of shapes. Because their facet counts and facet arrangements are the same, modified brilliants also look (in terms of brilliance and fire interplay) the most like round brilliants and are therefore (in general and at present) the most saleable. Certain modified round brilliants also exhibit better Diamond Light Performance

Modified brilliants include the marquise or navette (French for "little boat", because it resembles the hull of a sailboat), heart, triangular trillion (also trillian or trilliant), oval, and the pear or drop cuts. These are the most commonly encountered modified brilliants; modern cutting technology has allowed the development of increasingly complex and hitherto unthinkable shapes, such as stars and butterflies. Their proportions are mostly a matter of personal preference; however, due to their sharp terminations and diamond's relative fragility, these cuts are more vulnerable to accidental breakage and may therefore be more difficult to insure.

There are several older modified brilliant cuts of uncertain age that, while no longer widely used, are notable for history's sake. They are all round in outline and modify the standard round brilliant by adding facets and changing symmetry, either by dividing the standard facets or by placing new ones in different arrangements. These cuts include: the King and Magna cut, both developed by New York City firms, with the former possessing 86 facets and 12-fold symmetry and the latter with 102 facets and 10-fold symmetry; the High-Light cut, developed by Belgian cutter M. Westreich, with 16 additional facets divided equally between the crown and pavilion; and the Princess 144, introduced in the 1960s, with 144 facets and 8-fold symmetry. Not to be confused with the mixed Princess cut, the Princess 144 cut makes for a lively stone with good scintillation; the extra facets are cut under the girdle rather than subdivided. The extra care required for these sub-girdle facets benefits the finished stone by mitigating girdle irregularity and bearding (hairline fracturing). Today, with increase understanding of light dynamics and diamond cutting, many company's have developed new modified round brilliant cut diamonds. If designed correctly these extra facets of the modified round brilliant could benefit the over beauty of a diamond, such as in 91 facet diamonds. Especially with in the movement toward Diamond Light Performance.

Step cuts

Stones whose outlines are either square or rectangular and whose facets are rectilinear and arranged parallel to the girdle are known as step- or trap-cut stones. These stones often have their corners truncated, creating an emerald cut (after its most common application to emerald gemstones) with an octagonal outline. This is done because sharp corners are points of weakness where a diamond may cleave or fracture. Instead of a culet, step-cut stones have a keel running the length of the pavilion terminus. Because both the pavilion and crown are comparatively shallow, step cut stones are generally not as bright and never as fiery as brilliant cut stones, but rather accentuate a diamond's clarity (as even the slightest flaw would be highly visible), whiteness, and lustre (and therefore good polish).

Due to the current vogue for brilliant and brilliant-like cuts, step cut diamonds may suffer somewhat in value; stones that are deep enough may be re-cut into more popular shapes. However, the step cut's rectilinear form was very popular in the Art Deco period. Antique jewelry of the period features step-cut stones prominently, and there is a market in producing new step-cut stones to repair antique jewelry or to reproduce it. The slender, rectangular baguette (from the French, resembling a loaf of bread) was and is the most common form of the step cut: today, it is most often used as an accent stone to flank a ring's larger central (and usually brilliant-cut) stone.

Square step cuts whose corners are not truncated are known as carré; they are also characteristic of antique jewelry. They may resemble the square-shaped Princess cut in passing, but a carré's lack of fire and simpler facets are distinctive. They may or may not have a culet. In Western jewelry dating to before the advent of brilliant-type cuts, very shallow step-cut stones were used as lustrous covers for miniature paintings: these are known in the antique trade as portrait stones. Characteristic of Indian jewelry are lasque diamonds, which may be the earliest form of step cut. They are flat stones with large tables and asymmetric outlines.

Other forms of the step cut include triangle, kite, lozenge, trapeze (or trapezoid), and obus.

Mixed cuts

Mixed cuts share aspects of both (modified) brilliant and step cuts: they are meant to combine the weight preservation and dimensions of step cuts with the optical effects of brilliants. Typically the crown is step-cut and the pavilion brilliant-cut. Mixed cuts are all relatively new, with the oldest dating back to the 1960s. They have been extremely successful commercially and continue to gain popularity, loosening the foothold of the de facto standard round brilliant.

Among the first mixed cuts was the Barion cut, introduced in 1971. Invented by South African diamond cutter Basil Watermeyer and named after himself and his wife Marion, the basic Barion cut is an octagonal square or rectangle, with a polished and faceted girdle. The total facet count is 62 (excluding the culet): 25 on the crown; 29 on the pavilion; and 8 on the girdle. This cut can be easily identified by the characteristic central cross pattern (as seen through the table) created by the pavilion facets, as well as by the crescent-shaped facets on the pavilion. A similar cut is the Radiant cut: It differs in having a total of 70 facets. Both it and the Barion cut exist in a large number of modified forms, with slightly different facet arrangements and combinations.

The most successful mixed cut is the Princess cut, first introduced in 1960 by A. Nagy of London. It was originally intended for flat rough (macles), but has since become popular enough that some gemological labs, such as that of the American Gem Society (AGS), have developed Princess cut grading standards with stringency akin to standards applied to round brilliants. Its higher fire and brilliance compared to other mixed cuts is one reason for the Princess cut's popularity, but more importantly is the fact that, of all the diamond cuts, it wastes the least of the original crystal.

Rose cuts

Various forms of the rose cut have been in use since the mid 16th century. Like the step cuts, they were derived from older types of cuts (see History section). The basic rose cut has a flat base (no pavilion) and a crown composed of triangular facets (usually 12 or 24) in symmetrical arrangement, which rise to form a point. They are usually circular in outline; variations include: the briolette (oval); Antwerp rose (hexagonal); and double Dutch rose (resembling two rose cuts united back-to-back).

Rose cuts are seldom seen nowadays, except in antique jewelry. Like the older style brilliants and step cuts, there is a growing demand for rose cuts for the purpose of repairing or reproducing antique pieces. The rose cut is still routinely used for melée diamonds.

Cut grading

File:Ideal cut dm.jpg

Light dispersion from an "ideal cut" diamond simulant. Notice the near-perfect symmetry of the light reflected out of the stone.

The "Cut" of the "4-Cs" is the most difficult part for a consumer to judge when selecting a good diamond. This is because some certificates, such as those issued by the Gemological Institute of America, will not show the important measurements influencing cut (such as the pavilion angle and crown angle) and will not provide a subjective ranking of how good the cut was. The other 3-Cs can be ranked simply by the rating in each category. It requires a trained eye to judge the quality of a diamond cut, and the task is complicated by the fact that different standards are used in different countries (see proportions of the round brilliant).

The relationship between the crown angle and the pavilion angle has the greatest effect on the look of the diamond. A slightly steep pavilion angle can be complemented by a shallower crown angle, and vice versa. Graphs showing this trade-off are available from folds.net, by pressing Go on the HCA web service, and in Bruce Harding's article on Faceting Limits.

Other proportions also affect the look of the diamond:

The table ratio is very significant.
The length of the lower girdle facets affects whether Hearts and arrows can be seen in the stone, under certain viewers.
Indexing the upper girdle facets
- Most round brilliant diamonds have roughly the same girdle thickness at all 16 "thick parts".
- So-called "cheated" girdles have thicker girdles where the main facets touch the girdle than where adjacent upper girdle facets touch the girdle. These stones weigh more (for a given diameter, average girdle thickness, crown angle, pavilion angle, and table ratio), and have worse optical performance (their upper girdle facets appear dark in some lighting conditions).
- So-called "painted" girdles have thinner girdles where the main facets touch the girdle than where adjacent upper girdle facets touch the girdle. These stones have less light leakage at the edge of the stone (for a given crown angle, pavilion angle, and table ratio), but does have a negative effect on the overall beauty of a diamond as shown in the GIA article Painting and Digging Out.
- Solasfera is the only branded round modified brilliant diamond known to date that has no light leakage through out the stone and does not have any cheated or painted girdle, thus having more efficient and better optical performance.

Several groups have developed diamond cut grading standards.

The AGA standards may be the strictest. David Atlas (who developed the AGA standards) has suggested that they are overly strict.
The HCA changed several times between 2001 and 2004. As of 2004, an HCA score below two represented an excellent cut. The HCA distinguishes between brilliant, Tolkowsky, and fiery cuts.
The AGS standards changed in 2005 to better match Tolkowsky's model and Octonus' ray tracing results. The 2005 AGS standards penalize stones with "cheated" girdles.

The distance from the viewer's eye to the diamond is important. The 2005 AGS cut standards are based on a distance of 25 centimeters (about 10 inches). The 2004 HCA cut standards are based on a distance of 40 centimeters (about 16 inches). The GIA announced in the fall of 2005 that it will include a cut grade for round brilliant diamonds on every GIA Diamond Grading Report starting on January 1st, 2006. The single descriptive words are as follows: Excellent, Very Good, Good, Fair, and Poor.

References

Bruton, Eric. (1979). Diamonds, 2nd ed. Chilton Book Co. ISBN 0801967899
Cipriani, Curzio, Borelli, Alessandro, and Lyman, Kennie (US ed.) (1986). Simon & Schuster's Guide to Gems and Precious Stones, pp. 58–68. Simon & Schuster, Inc.; New York, New York. ISBN 0671604309
Pagel-Theisen, Verena. (2001). Diamond grading ABC: The manual (9th ed.), pp. 176–268. Rubin & Son n.v.; Antwerp, Belgium. ISBN 3980043460
Tolkowsky, Marcel (1919). Diamond Design: A Study of the Reflection and Refraction of Light in a Diamond. London: E. & F.N. Spon, Ltd. (Web edition as edited by Jasper Paulsen, Seattle, 2001.)
OctoNus Software has posted several diamond cut studies, by various authors. OctoNus, Moscow State University, Bruce Harding, and others have posted work there.
Holloway, Garry (2000-2004). HCA: defining ideal cut diamonds is a detailed explanation of the "Holloway Cut Advisor". A web service that uses this software is available.
Yantzer, Peter (March 2005). The effects of indexed upper half facets. (Retrieved March 19, 2005.)
GIA Various authors (2006). Painting and Digging Out, GIA article 2006.
Various authors (2004). Pricescope discussion on "cheated" girdles. (Retrieved March 19, 2005.)
GIA Various authors (2001) - Tolkowsky limitations. What did Tolkowsky really say?