Adaptive Huffman coding: Difference between revisions
m Minor formatting. |
m Minor Formatting |
||
| Line 43: | Line 43: | ||
====Example==== |
====Example==== |
||
[[File:Adaptive Huffman Vitter.jpg]]Encoding "abb" gives 01100001 001100010 11. |
|||
[[File:Adaptive Huffman Vitter.jpg]] |
|||
Step 1: |
Step 1: |
||
Revision as of 13:08, 16 March 2016
Adaptive Huffman coding (also called Dynamic Huffman coding) is an adaptive coding technique based on Huffman coding. It permits building the code as the symbols are being transmitted, having no initial knowledge of source distribution, that allows one-pass encoding and adaptation to changing conditions in data.
The benefit of one-pass procedure is that the source can be encoded in real time, though it becomes more sensitive to transmission errors, since just a single loss ruins the whole code.
Algorithms
There are a number of implementations of this method, the most notable are FGK (Faller-Gallager-Knuth) and Vitter algorithm.
FGK Algorithm
It is an online coding technique based on Huffman coding. Having no initial knowledge of occurrence frequencies, it permits dynamically adjusting the Huffman's tree as data are being transmitted. In a FGK Huffman tree, a special external node, called 0-node, is used to identify a newly-coming character. That is, whenever a new data is encountered, output the path to the 0-node followed by the data. For a past-coming character, just output the path of the data in the current Huffman's tree. Most importantly, we have to adjust the FGK Huffman tree if necessary, and finally update the frequency of related nodes. As the frequency of a datum is increased, the sibling property of the Huffman's tree may be broken. The adjustment is triggered for this reason. It is accomplished by consecutive swappings of nodes, subtrees, or both. The data node is swapped with the highest-ordered node of the same frequency in the Huffman's tree, (or the subtree rooted at the highest-ordered node). All ancestor nodes of the node should also be processed in the same manner.
Since the FGK Algorithm has some drawbacks about the node-or-subtree swapping, Vitter proposed another algorithm to improve it.
Vitter algorithm
Code is represented as a tree structure in which every node has a corresponding weight and a unique number.
Numbers go down, and from right to left.
Weights must satisfy the sibling property, which states that nodes must be listed in the order of decreasing weight with each node adjacent to its sibling. Thus if A is the parent node of B and C is a child of B, then .
The weight is merely the count of symbols transmitted which codes are associated with children of that node.
A set of nodes with same weights make a block.
To get the code for every node, in case of binary tree we could just traverse all the path from the root to the node, writing down (for example) "1" if we go to the right and "0" if we go to the left.
We need some general and straightforward method to transmit symbols that are "not yet transmitted" (NYT). We could use, for example, transmission of binary numbers for every symbol in alphabet.
Encoder and decoder start with only the root node, which has the maximum number. In the beginning it is our initial NYT node.
When we transmit an NYT symbol, we have to transmit code for the NYT node, then for its generic code.
For every symbol that is already in the tree, we only have to transmit code for its leaf node.
For every symbol transmitted both the transmitter and receiver execute the update procedure:
- If current symbol is NYT, add two child nodes to NYT node. One will be a new NYT node, the other is a leaf node for our symbol. Increase weight for the new leaf node and the old NYT and go to step 4. If current symbol is not NYT, go to symbol's leaf node.
- If this node does not have the highest number in a block, swap it with the node having the highest number, except if that node is its parent[1]
- Increase weight for current node
- If this is not the root node go to parent node then go to step 2. If this is the root, end.
Note: swapping nodes means swapping weights and corresponding symbols, but not the numbers. Notice that although the above description is excellent in capturing the principle of adaptive Huffman coding, it doesn't maintain Vitter's invariant that all leaves of weight w precede (in the implicit numbering) all internal nodes of weight w. See the example below for a more accurate explanation for Vittter's algorithm[1].
Example
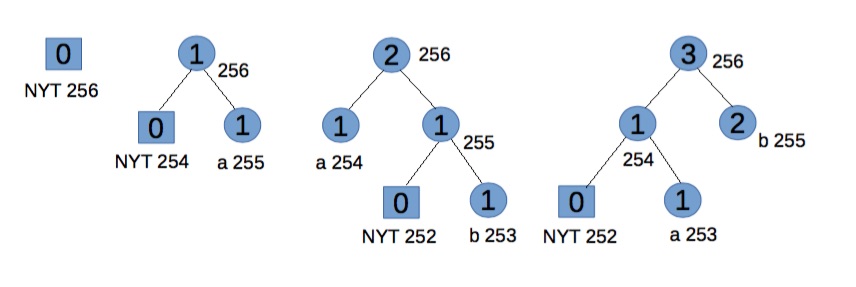 Encoding "abb" gives 01100001 001100010 11.
Encoding "abb" gives 01100001 001100010 11.
Step 1:
Start with an empty tree.
For "a" transmit its binary code.
Step 2:
NYT spawns two child nodes: 254 and 255, both with weight 0. Increase weight for root and 255. Code for "a", associated with node 255, is 1.
For "b" transmit 0 (for NYT node) then its binary code.
Step 3:
NYT spawns two child nodes: 252 for NYT and 253 for leaf node, both with weight 0. Increase weights for 253, 254, and root. To maintain Vitter’s invariant that all leaves of weight w precede (in the implicit numbering) all internal nodes of weight w, the branch starting with node 254 should be swop (in terms of symbols and weights, but not number ordering) with node 255. Code for "b" is 11.
For the second "b" transmit 11.
It should be noted that for the convenience of explanation this step doesn't exactly follow Vitter's algorithm[1], but the effects are equivalent.
Step 4:
Go to leaf node 253. Notice we have two blocks with weight 1. Node 253 and 254 is one block (consisting of leaves), node 255 is another block (consisting of internal nodes). For node 253, the biggest number in its block is 254, so swap the weights and symbols of nodes 253 and 254. Now node 254 and the branch starting from node 255 satisfy the SlideAndIncrement condition[1] and hence must be swop. At last increase node 255 and 256’s weight.
Future code for "b" is 1, and for "a" is now 01, which reflects their frequency.
References
- ^ a b c d "Adaptive Huffman Coding". Cs.duke.edu. Retrieved 2012-02-26.
- Vitter's original paper: J. S. Vitter, "Design and Analysis of Dynamic Huffman Codes", Journal of the ACM, 34(4), October 1987, pp 825–845.
- J. S. Vitter, "ALGORITHM 673 Dynamic Huffman Coding", ACM Transactions on Mathematical Software, 15(2), June 1989, pp 158–167. Also appears in Collected Algorithms of ACM.
- Donald E. Knuth, "Dynamic Huffman Coding", Journal of Algorithm, 6(2), 1985, pp 163–180.
External links
 This article incorporates public domain material from Paul E. Black. "adaptive Huffman coding". Dictionary of Algorithms and Data Structures. NIST.
This article incorporates public domain material from Paul E. Black. "adaptive Huffman coding". Dictionary of Algorithms and Data Structures. NIST.- University of California Dan Hirschberg site
- Cardiff University Dr. David Marshall site
- C implementation of Vitter algorithm
- Excellent description from Duke University

