Line drawing algorithm

Two rasterized lines. The colored pixels are shown as circles. Above: monochrome screening; below: Gupta-Sproull anti-aliasing; the ideal line is considered here as a surface.

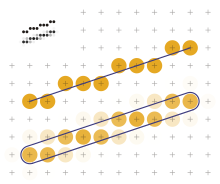
A line drawing algorithm is a graphical algorithm for approximating a line segment on discrete graphical media. On discrete media, such as pixel-based displays and printers, line drawing requires such an approximation (in nontrivial cases). Basic algorithms rasterize lines in one color. A better representation with multiple color gradations requires an advanced process, spatial anti-aliasing.

On continuous media, by contrast, no algorithm is necessary to draw a line. For example, oscilloscopes use natural phenomena to draw lines and curves.

The Cartesian slope-intercept equation for a straight line is $Y=mx+b$ With m representing the slope of the line and b as the y intercept. Given that the two endpoints of the line segment are specified at positions $(x1,y1)$ and $(x2,y2)$. we can determine values for the slope m and y intercept b with the following calculations, $m=(y2-y1)/(x2-x1)$ so, $b=y1-m.x1$.

A naive line-drawing algorithm

The simplest method of screening is the direct drawing of the equation defining the line.

dx = x2 - x1
dy = y2 - y1
for x from x1 to x2 {
  y = y1 + dy * (x - x1) / dx
  plot(x, y)
}

It is assumed here that the points have already been ordered so that $x_{2}>x_{1}$. This algorithm works just fine when $dx>=dy$ (i.e., slope is less than or equal to 1), but if $dx<dy$ (i.e., slope greater than 1), the line becomes quite sparse with lots of gaps, and in the limiting case of $dx=0$, only a single point is plotted.

The naïve line drawing algorithm is inefficient and thus, slow on a digital computer. Its inefficiency stems from the number of operations and the use of floating-point calculations. Line drawing algorithms such as Bresenham's or Wu's are preferred instead.

List of line drawing algorithms

Lines using Xiaolin Wu's algorithm, showing "ropey" appearance.

The following is a partial list of line drawing algorithms:

• Digital Differential Analyzer (graphics algorithm) — Similar to the naive line-drawing algorithm, with minor variations.
• Bresenham's line algorithm — optimized to use only additions (i.e. no divisions or multiplications); it also avoids floating-point computations.
• Xiaolin Wu's line algorithm — can perform spatial anti-aliasing, appears "ropey" from brightness varying along the length of the line
• Gupta-Sproull algorithm

References

Fundamentals of Computer Graphics, 2nd Edition, A.K. Peters by Peter Shirley