Generalised beam theory: Difference between revisions
Added {{uncategorized}} tag to article (TW) |
mos |
||
| Line 1: | Line 1: | ||
'''Generalised beam theory (GBT)''' is the most complete and disseminated [[beam theory]] to be formulated and extensively validated. Its origin is due to Richard Schardt (1966), a German scientist from the University of Darmstadt. Since then many other authors have extended the initial (first-order elastic) GBT formulations developed by Schardt and his co-workers.<ref>{{cite journal|last1=Schardt|first1=Richard|title=Generalised Beam Theory – an adequate method for coupled stability problems|journal=Thin-Walled Strcutures|date=1994|volume=19|issue=2-4|pages=161–180|doi=10.1016/0263-8231(94)90027-2}}</ref><ref>{{cite journal|last1=Davies|first1=JM|title=Recent research advances in cold-formed steel structures|journal=Journal of Constructional Steel Research|date=2000|volume=55|issue=1-3|doi=10.1016/S0143-974X(99)00089-9|pages=267-288}}</ref> However, it is fair to say that a vast majority of the most advanced/complete (in order to predict as close as possible the real behaviour (collapse and post-collapse) of a structural member) formulations and applications of GBT have been developed by the research group headed by Dinar Camotim, a full professor from the University of Lisbon, Portugal, since the beginning of the 21st century |
'''Generalised beam theory (GBT)''' is the most complete and disseminated [[beam theory]] to be formulated and extensively validated. Its origin is due to Richard Schardt (1966), a German scientist from the University of Darmstadt. Since then many other authors have extended the initial (first-order elastic) GBT formulations developed by Schardt and his co-workers.<ref>{{cite journal|last1=Schardt|first1=Richard|title=Generalised Beam Theory – an adequate method for coupled stability problems|journal=Thin-Walled Strcutures|date=1994|volume=19|issue=2-4|pages=161–180|doi=10.1016/0263-8231(94)90027-2}}</ref><ref>{{cite journal|last1=Davies|first1=JM|title=Recent research advances in cold-formed steel structures|journal=Journal of Constructional Steel Research|date=2000|volume=55|issue=1-3|doi=10.1016/S0143-974X(99)00089-9|pages=267-288}}</ref> However, it is fair to say that a vast majority of the most advanced/complete (in order to predict as close as possible the real behaviour (collapse and post-collapse) of a structural member) formulations and applications of GBT have been developed by the research group headed by Dinar Camotim, a full professor from the University of Lisbon, Portugal, since the beginning of the 21st century. |
||
<ref>{{cite journal|last1=Silvestre|first1=N|last2=Camotim|first2=D|title=Second-order generalised beam theory for arbitrary orthotropic materials|journal=Thin-Walled Strcutures|date=2002|volume=40|issue=9|pages=791-820|doi=10.1016/S0263-8231(02)00026-5}}</ref><ref>{{cite journal|last1=Borges Dinis|first1=P|last2=Camotim|first2=D|last3=Silvestre|first3=N|title=GBT formulation to analyse the buckling behaviour of thin-walled members with arbitrarily ‘branched’open cross-sections|journal=Thin-Walled Strcutures|date=2006|volume=44|issue=1|pages=20-38|doi=10.1016/j.tws.2005.09.005}}</ref><ref>{{cite journal|last1=Camotim|first1=D|last2=Basaglia|first2=C|last3=Silvestre|first3=N|title=GBT buckling analysis of thin-walled steel frames: a state-of-the-art report|journal=Thin-Walled Strcutures|date=2010|volume=48|issue=10|pages=726-743|doi=10.1016/j.tws.2009.12.003}}</ref><ref>{{cite journal|last1=Abambres|first1=M|last2=Camotim|first2=D|last3=Silvestre|first3=N|title=GBT-based elastic–plastic post-buckling analysis of stainless steel thin-walled members|journal=Thin-Walled Strcutures|date=2014|volume=83|issue=October|pages=85-102|doi=10.1016/j.tws.2014.01.004}}</ref><ref>{{cite journal|last1=Abambres|first1=M|last2=Camotim|first2=D|last3=Silvestre|first3=N|last4=Rasmussen|first4=KJR|title=GBT-based structural analysis of elastic–plastic thin-walled members|journal=Computers & Structures|date=2014|volume=136|issue=May|pages=1-23|doi=10.1016/j.compstruc.2014.01.001}}</ref><ref>{{cite journal|last1=Bebiano|first1=R|last2=Gonçalves|first2=R|last3=Camotim|first3=D|title=A cross-section analysis procedure to rationalise and automate the performance of GBT-based structural analyses|journal=Thin-Walled Strcutures|date=2015|volume=92|issue=July|pages=29-47|doi=10.1016/j.tws.2015.02.017}}</ref><ref>{{cite journal|last1=Gonçalves|first1=R|last2=Camotim|first2=D|title=GBT deformation modes for curved thin-walled cross-sections based on a mid-line polygonal approximation|journal=Thin-Walled Strcutures|date=2016|issue=January|doi=10.1016/j.tws.2015.12.025}}</ref> |
|||
<ref>{{cite journal|last1=Silvestre|first1=N|last2=Camotim|first2=D|title=Second-order generalised beam theory for arbitrary orthotropic materials|journal=Thin-Walled Strcutures|date=2002|volume=40|issue=9|pages=791-820|doi=10.1016/S0263-8231(02)00026-5}}</ref> |
|||
<ref>{{cite journal|last1=Borges Dinis|first1=P|last2=Camotim|first2=D|last3=Silvestre|first3=N|title=GBT formulation to analyse the buckling behaviour of thin-walled members with arbitrarily ‘branched’open cross-sections|journal=Thin-Walled Strcutures|date=2006|volume=44|issue=1|pages=20-38|doi=10.1016/j.tws.2005.09.005}}</ref> |
|||
<ref>{{cite journal|last1=Camotim|first1=D|last2=Basaglia|first2=C|last3=Silvestre|first3=N|title=GBT buckling analysis of thin-walled steel frames: a state-of-the-art report|journal=Thin-Walled Strcutures|date=2010|volume=48|issue=10|pages=726-743|doi=10.1016/j.tws.2009.12.003}}</ref> |
|||
<ref>{{cite journal|last1=Abambres|first1=M|last2=Camotim|first2=D|last3=Silvestre|first3=N|title=GBT-based elastic–plastic post-buckling analysis of stainless steel thin-walled members|journal=Thin-Walled Strcutures|date=2014|volume=83|issue=October|pages=85-102|doi=10.1016/j.tws.2014.01.004}}</ref> |
|||
<ref>{{cite journal|last1=Abambres|first1=M|last2=Camotim|first2=D|last3=Silvestre|first3=N|last4=Rasmussen|first4=KJR|title=GBT-based structural analysis of elastic–plastic thin-walled members|journal=Computers & Structures|date=2014|volume=136|issue=May|pages=1-23|doi=10.1016/j.compstruc.2014.01.001}}</ref> |
|||
<ref>{{cite journal|last1=Bebiano|first1=R|last2=Gonçalves|first2=R|last3=Camotim|first3=D|title=A cross-section analysis procedure to rationalise and automate the performance of GBT-based structural analyses|journal=Thin-Walled Strcutures|date=2015|volume=92|issue=July|pages=29-47|doi=10.1016/j.tws.2015.02.017}}</ref> |
|||
<ref>{{cite journal|last1=Gonçalves|first1=R|last2=Camotim|first2=D|title=GBT deformation modes for curved thin-walled cross-sections based on a mid-line polygonal approximation|journal=Thin-Walled Strcutures|date=2016|issue=January|doi=10.1016/j.tws.2015.12.025}}</ref> (please follow the [http://www.civil.ist.utl.pt/gbt <u>website of his research group</u>] for information on publications and available software). |
|||
The theory can be applied without restrictions to any prismatic |
The theory can be applied without restrictions to any prismatic thin-walled structural member exhibiting straight or curved axial axis (any loading, any cross-section geometry, any boundary conditions), and it is a very promising alternative to the powerful Finite Element Method employing 2D or 3D FEs to predict the member structural behaviour. |
||
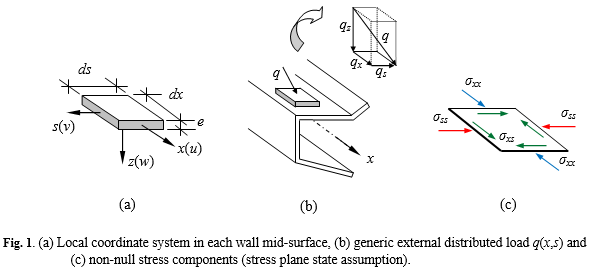
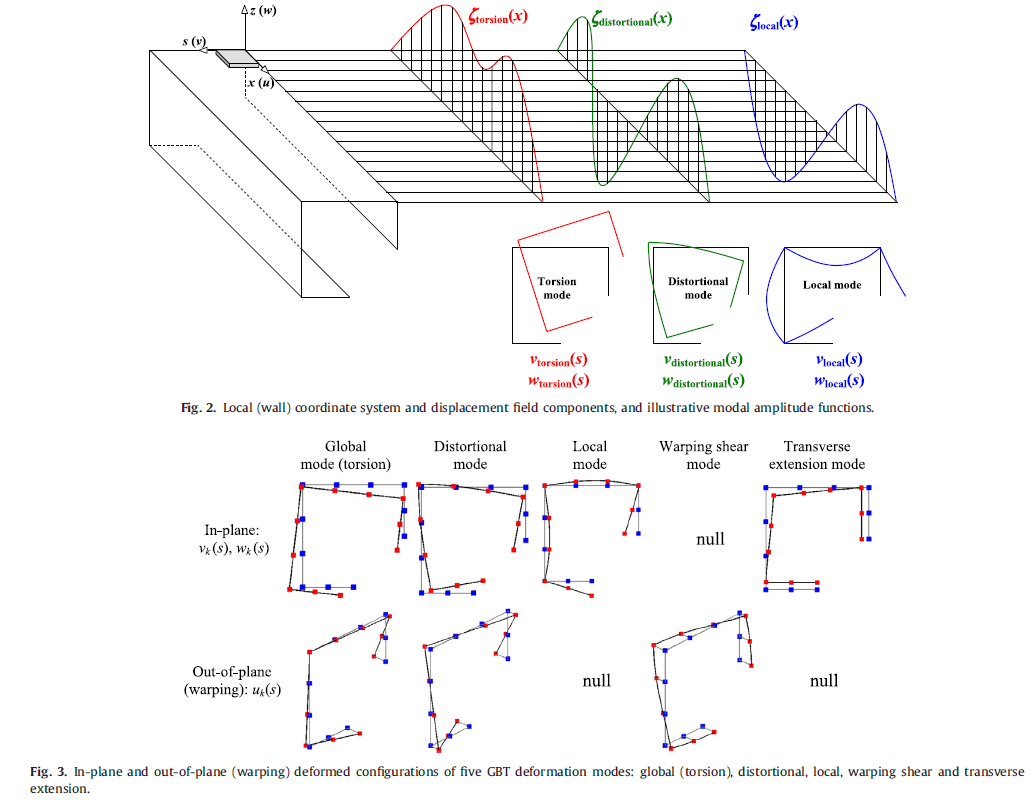
GBT has already been widely recognised as a powerful, versatile, elegant and efficient approach to analyse thin-walled members and structural systems. The elegance and efficiency arise mostly from its rather unique modal nature – the displacement field is expressed as a linear combination of cross-section deformation modes whose amplitudes vary continuously along the member length (x axis) - see Figures 2-3. Due to GBT assumptions inherent to a thin-walled member, only 3 non-null stress components are considered in the formulations (see Fig. 1). |
GBT has already been widely recognised as a powerful, versatile, elegant and efficient approach to analyse thin-walled members and structural systems. The elegance and efficiency arise mostly from its rather unique modal nature – the displacement field is expressed as a linear combination of cross-section deformation modes whose amplitudes vary continuously along the member length (x axis) - see Figures 2-3. Due to GBT assumptions inherent to a thin-walled member, only 3 non-null stress components are considered in the formulations (see Fig. 1). |
||
| Line 23: | Line 17: | ||
<!-- [[File:GBT membrane displacement field.png|GBT membrane displacement field]] --> |
<!-- [[File:GBT membrane displacement field.png|GBT membrane displacement field]] --> |
||
The GBT modal nature makes it possible to (i) acquire in-depth knowledge on the mechanics of the thin-walled member behaviour and (ii) judiciously exclude, from subsequent similar GBT analyses, those deformation modes found to play no (or negligible) role in the particular behaviour under scrutiny, thus further reducing the number of d.o.f. involved in a GBT analysis (i.e., increasing its computational efficiency). GBT has already extensively prooved its potential regarding (1) deep understanding of the structural behaviour under analysis as well as (2) computational efficiency (i.e., number of degrees of freedom involved in the analysis |
The GBT modal nature makes it possible to (i) acquire in-depth knowledge on the mechanics of the thin-walled member behaviour and (ii) judiciously exclude, from subsequent similar GBT analyses, those deformation modes found to play no (or negligible) role in the particular behaviour under scrutiny, thus further reducing the number of d.o.f. involved in a GBT analysis (i.e., increasing its computational efficiency). GBT has already extensively prooved its potential regarding (1) deep understanding of the structural behaviour under analysis as well as (2) computational efficiency (i.e., number of degrees of freedom involved in the analysis). |
||
The investigation, application and dissemination of GBT will certainly last during many more years. |
The investigation, application and dissemination of GBT will certainly last during many more years. |
||
Revision as of 19:43, 8 December 2017
Generalised beam theory (GBT) is the most complete and disseminated beam theory to be formulated and extensively validated. Its origin is due to Richard Schardt (1966), a German scientist from the University of Darmstadt. Since then many other authors have extended the initial (first-order elastic) GBT formulations developed by Schardt and his co-workers.[1][2] However, it is fair to say that a vast majority of the most advanced/complete (in order to predict as close as possible the real behaviour (collapse and post-collapse) of a structural member) formulations and applications of GBT have been developed by the research group headed by Dinar Camotim, a full professor from the University of Lisbon, Portugal, since the beginning of the 21st century. [3][4][5][6][7][8][9]
The theory can be applied without restrictions to any prismatic thin-walled structural member exhibiting straight or curved axial axis (any loading, any cross-section geometry, any boundary conditions), and it is a very promising alternative to the powerful Finite Element Method employing 2D or 3D FEs to predict the member structural behaviour.
GBT has already been widely recognised as a powerful, versatile, elegant and efficient approach to analyse thin-walled members and structural systems. The elegance and efficiency arise mostly from its rather unique modal nature – the displacement field is expressed as a linear combination of cross-section deformation modes whose amplitudes vary continuously along the member length (x axis) - see Figures 2-3. Due to GBT assumptions inherent to a thin-walled member, only 3 non-null stress components are considered in the formulations (see Fig. 1).
Membrane displacement field (i.e., in the cross-section mid-surface):
The GBT modal nature makes it possible to (i) acquire in-depth knowledge on the mechanics of the thin-walled member behaviour and (ii) judiciously exclude, from subsequent similar GBT analyses, those deformation modes found to play no (or negligible) role in the particular behaviour under scrutiny, thus further reducing the number of d.o.f. involved in a GBT analysis (i.e., increasing its computational efficiency). GBT has already extensively prooved its potential regarding (1) deep understanding of the structural behaviour under analysis as well as (2) computational efficiency (i.e., number of degrees of freedom involved in the analysis).
The investigation, application and dissemination of GBT will certainly last during many more years.
References
- ^ Schardt, Richard (1994). "Generalised Beam Theory – an adequate method for coupled stability problems". Thin-Walled Strcutures. 19 (2–4): 161–180. doi:10.1016/0263-8231(94)90027-2.
- ^ Davies, JM (2000). "Recent research advances in cold-formed steel structures". Journal of Constructional Steel Research. 55 (1–3): 267–288. doi:10.1016/S0143-974X(99)00089-9.
- ^ Silvestre, N; Camotim, D (2002). "Second-order generalised beam theory for arbitrary orthotropic materials". Thin-Walled Strcutures. 40 (9): 791–820. doi:10.1016/S0263-8231(02)00026-5.
- ^ Borges Dinis, P; Camotim, D; Silvestre, N (2006). "GBT formulation to analyse the buckling behaviour of thin-walled members with arbitrarily 'branched'open cross-sections". Thin-Walled Strcutures. 44 (1): 20–38. doi:10.1016/j.tws.2005.09.005.
- ^ Camotim, D; Basaglia, C; Silvestre, N (2010). "GBT buckling analysis of thin-walled steel frames: a state-of-the-art report". Thin-Walled Strcutures. 48 (10): 726–743. doi:10.1016/j.tws.2009.12.003.
- ^ Abambres, M; Camotim, D; Silvestre, N (2014). "GBT-based elastic–plastic post-buckling analysis of stainless steel thin-walled members". Thin-Walled Strcutures. 83 (October): 85–102. doi:10.1016/j.tws.2014.01.004.
- ^ Abambres, M; Camotim, D; Silvestre, N; Rasmussen, KJR (2014). "GBT-based structural analysis of elastic–plastic thin-walled members". Computers & Structures. 136 (May): 1–23. doi:10.1016/j.compstruc.2014.01.001.
- ^ Bebiano, R; Gonçalves, R; Camotim, D (2015). "A cross-section analysis procedure to rationalise and automate the performance of GBT-based structural analyses". Thin-Walled Strcutures. 92 (July): 29–47. doi:10.1016/j.tws.2015.02.017.
- ^ Gonçalves, R; Camotim, D (2016). "GBT deformation modes for curved thin-walled cross-sections based on a mid-line polygonal approximation". Thin-Walled Strcutures (January). doi:10.1016/j.tws.2015.12.025.
This article has not been added to any content categories. Please help out by adding categories to it so that it can be listed with similar articles. (November 2017) |