Hyperbolic functions

In mathematics, the hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. They are:

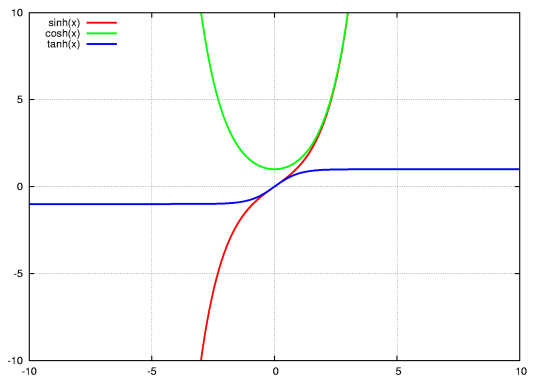
sinh, cosh and tanh

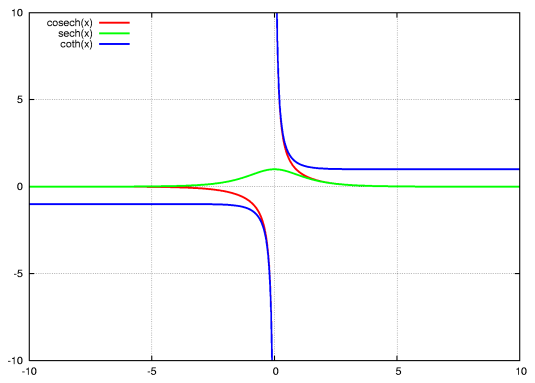
csch, sech and coth

$\sinh(x)={\frac {(e^{x}-e^{-x})}{2}}=-i\sin(ix)$

(hyperbolic sine, pronounced "shine" or "sinch")

$\cosh(x)={\frac {(e^{x}+e^{-x})}{2}}$

(hyperbolic cosine, pronounced "cosh")

$\tanh(x)={\frac {\sinh(x)}{\cosh(x)}}=-i\tan(ix)$

(hyperbolic tangent, pronounced "than" or "tanch")

$\coth(x)={\frac {\cosh(x)}{\sinh(x)}}$

(hyperbolic cotangent, pronounced "coth")

$\operatorname {sech} (x)={\frac {1}{\cosh(x)}}$

(hyperbolic secant, pronounced "sheck" or "sech")

$\operatorname {csch} (x)={\frac {1}{\sinh(x)}}$

(hyperbolic cosecant, pronounced "cosheck" or "cosech")

Relationship to regular trigonometric functions

Just as the points (cos t, sin t) define a circle, the points (cosh t, sinh t) define the equilateral hyperbola x² - y² = 1. This is based on the easily verified identity

$(\cosh t)^{2}-(\sinh t)^{2}=1.\,$

However, the hyperbolic functions are not periodic.

The parameter t is not a circular angle, but rather a hyperbolic angle which represents twice the area between the x-axis, the hyperbola and the straight line which links the origin with the point (cosh t, sinh t) on the hyperbola.

The function cosh x is an even function, that is symmetric with respect to the y-axis, and cosh 0 = 1

The function sinh x is an odd function, that is symmetric with respect to the origin, and sinh 0 = 0

The hyperbolic functions satisfy many identities, all of them similar in form to the trigonometric identities. In fact, Osborne's rule states that one can convert any trigonometric identity into a hyperbolic identity by expanding it completely in terms of integral powers of sines and cosines, changing sine to sinh and cosine to cosh, and switching the sign of every term which contains a product of two sinh's. This yields for example the addition theorems

$\sinh(x+y)=\sinh(x)\cosh(y)+\cosh(x)\sinh(y)\,$

$\cosh(x+y)=\cosh(x)\cosh(y)+\sinh(x)\sinh(y)\,$

and the "half-angle formulas"

$\cosh ^{2}\left({\frac {x}{2}}\right)={\frac {1+\cosh(x)}{2}}$

$\sinh ^{2}\left({\frac {x}{2}}\right)={\frac {\cosh(x)-1}{2}}$

The derivative of sinh x is given by cosh x and the derivative of cosh x is sinh x.

The graph of the function cosh x is the catenary curve.

Inverse hyperbolic functions

The inverses of the hyperbolic functions are

$\operatorname {arcsinh} (x)=\ln(x+{\sqrt {x^{2}+1}})$

$\operatorname {arccosh} (x)=\ln(x+{\sqrt {x^{2}-1}})$

$\operatorname {arctanh} (x)=\ln \left({\frac {\sqrt {1-x^{2}}}{1-x}}\right)={\begin{matrix}{\frac {1}{2}}\end{matrix}}\ln \left({\frac {1+x}{1-x}}\right)$

$\operatorname {arccoth} (x)=\ln \left({\frac {\sqrt {x^{2}-1}}{x-1}}\right)={\begin{matrix}{\frac {1}{2}}\end{matrix}}\ln \left({\frac {x+1}{x-1}}\right)$

$\operatorname {arcsech} (x)=\ln \left({\frac {1\pm {\sqrt {1-x^{2}}}}{x}}\right)$

$\operatorname {arccsch} (x)=\ln \left({\frac {1\pm {\sqrt {1+x^{2}}}}{x}}\right)$

Applications of Hyperbolic Functions to Integrals

$\int {\frac {dx}{\sqrt {1-x^{2}}}}=\operatorname {arcsin} (x)=-\operatorname {arccos} (x)+{\frac {\pi }{2}}$

$\int {\frac {dx}{\sqrt {x^{2}+1}}}=\operatorname {arcsinh} (x)=\ln(x+{\sqrt {x^{2}+1}})$

$\int {\frac {dx}{\sqrt {x^{2}-1}}}=\operatorname {arccosh} (x)=\ln(x+{\sqrt {x^{2}-1}})$

$\int {\sqrt {1-x^{2}}}dx={\frac {\operatorname {arcsin} (x)+x{\sqrt {1-x^{2}}}}{2}}$

$\int {\sqrt {x^{2}+1}}dx={\frac {\operatorname {arcsinh} (x)+x{\sqrt {x^{2}+1}}}{2}}={\frac {\ln(x+{\sqrt {x^{2}+1}})+x{\sqrt {x^{2}+1}}}{2}}$

$\int {\sqrt {x^{2}-1}}dx={\frac {-\operatorname {arccos} h(x)+x{\sqrt {x^{2}-1}}}{2}}={\frac {-\ln(x+{\sqrt {x^{2}-1}})+x{\sqrt {x^{2}-1}}}{2}}$

$\int {\frac {dx}{1+x^{2}}}=\operatorname {arctan} (x)$

$\int {\frac {dx}{1-x^{2}}}=\operatorname {arctanh} (x)={\begin{matrix}{\frac {1}{2}}\end{matrix}}\ln \left({\frac {1+x}{1-x}}\right)$

Hyperbolic functions for complex numbers

Since the exponential function can be defined for any complex argument, we can extend the definitions of the hyperbolic functions also to complex arguments. The functions sinh z and cosh z are then holomorphic; their Taylor series expansions are given in the Taylor series article.

Relationships to regular trigonometric functions are given by Euler's_formula for complex numbers:

$e^{ix}=\cos x+i\;\sin x$

$\cosh(ix)={\frac {(e^{ix}+e^{-ix})}{2}}=\cos(x)$

$\sinh(ix)={\frac {(e^{ix}-e^{-ix})}{2}}=i\sin(x)$

$\tanh(ix)=i\tan(x)\,$

$\sinh(x)=-i\sin(ix)\,$

$\cosh(x)=\cos(ix)\,$

$\tanh(x)=-i\tan(ix)\,$

$\operatorname {arcsinh} (x)=i\arcsin(-ix)$

$\operatorname {arccosh} (x)=i\arccos(x)$

$\operatorname {arctanh} (x)=i\arctan(-ix)$

See also

• List of coshes