Hidden Markov model

File:MarkovModel.png

State transitions in a hidden Markov model (example)
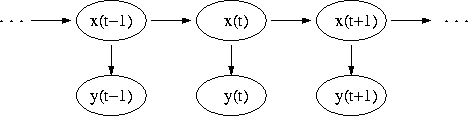
x — hidden states
y — observable outputs
a — transition probabilities
b — output probabilities

A hidden Markov model (HMM) is a statistical model where the system being modeled is assumed to be a Markov process with unknown parameters, and the challenge is to determine the hidden parameters from the observable parameters. The extracted model parameters can then be used to perform further analysis, for example for pattern recognition applications. A HMM can be considered as the simplest dynamic Bayesian network.

In a regular Markov model, the state is directly visible to the observer, and therefore the state transition probabilities are the only parameters. In a hidden Markov model, the state is not directly visible, but variables influenced by the state are visible. Each state has a probability distribution over the possible output tokens. Therefore the sequence of tokens generated by an HMM gives some information about the sequence of states.

Hidden Markov models are especially known for their application in temporal pattern recognition such as speech, handwriting, gesture recognition and bioinformatics.

Architecture of a Hidden Markov Model

The diagram below shows the general architecture of an HMM. Each oval shape represents a random variable that can adopt a number of values. The random variable $x(t)$ is the value of the hidden variable at time $t$. The random variable $y(t)$ is the value of the observed variable at time $t$. The arrows in the diagram denote conditional dependencies.

From the diagram, it is clear that the value of the hidden variable $x(t)$ (at time $t$) only depends on the value of the hidden variable $x(t-1)$ (at time $t-1$). This is called the Markov property. Similarly, the value of the observed variable $y(t)$ only depends on the value of the hidden variable $x(t)$ (both at time $t$).

Temporal evolution of a hidden Markov model

Probability of an observed sequence

The probability of observing a sequence $Y=y(0),y(1),...,y(L-1)$ of length $L$ is given by:

$P(Y)=\sum _{X}P(Y\mid X)P(X)$

where the sum runs over all possible hidden node sequences $X=x(0),x(1),...,x(L-1)$. A brute force calculation of $P(Y)$ is intractable for realistic problems, as the number of possible hidden node sequences typically is extremely high. The calculation can however be speeded up enormously using an algorithm called the forward-backward procedure .

Using Hidden Markov Models

There are 3 canonical problems associated with HMMs:

• Given the parameters of the model, compute the probability of a particular output sequence. This problem is solved by the forward-backward procedure.
• Given the parameters of the model, find the most likely sequence of hidden states that could have generated a given output sequence. This problem is solved by the Viterbi algorithm.
• Given an output sequence or a set of such sequences, find the most likely set of state transition and output probabilities. In other words, train the parameters of the HMM given a dataset of sequences. This problem is solved by the Baum-Welch algorithm.

A concrete example

This example is further elaborted in the Viterbi algorithm page.

Applications of hidden Markov models

• speech recognition , gesture and body motion recognition , optical character recognition
• machine translation
• bioinformatics and genomics
  • prediction of protein-coding regions in genome sequences
  • modelling families of related DNA or protein sequences
  • prediction of secondary structure elements from protein primary sequences
• and many more...

History

Hidden Markov Models were first described in a series of statistical papers by Leonard E. Baum and other authors in the second half of the 1960s. One of the first applications of HMMs was speech recognition, starting in the mid-1970s.

In the second half of the 1980s, HMMs began to be applied to the analysis of biological sequences, in particular DNA. Since then, they have become ubiquitous in the field of bioinformatics.

References

• Lawrence R. Rabiner, A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition. Proceedings of the IEEE, 77 (2), p. 257–286, February 1989.
• Richard Durbin, Sean R. Eddy, Anders Krogh, Graeme Mitchison. Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids. Cambridge University Press, 1999. ISBN 0-521-62971-3.
• Lior Pachter and Bernd Sturmfels. "Algebraic Statistics for Computational Biology" Cambridge University Press, 2005. ISBN 0-521-85700-7
• Kristie Seymore, Andrew McCallum, and Roni Rosenfeld. Learning Hidden Markov Model Structure for Information Extraction. AAAI 99 Workshop on Machine Learning for Information Extraction, 1999. (also at CiteSeer: [1])
• http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html
• J. Li, A. Najmi, R. M. Gray, Image classification by a two dimensional hidden Markov model, IEEE Transactions on Signal Processing, 48(2):517-33, February 2000.

See also

• Andrey Markov
• Baum-Welch algorithm
• Bayesian inference
• Estimation theory
• Viterbi algorithm
• Hierarchical hidden Markov model
• Hidden semi-Markov model

External links

• Hidden Markov Model (HMM) Toolbox for Matlab (by Kevin Murphy)
• Hidden Markov Model Toolkit (HTK) (a portable toolkit for building and manipulating hidden Markov models)
• Hidden Markov Models (an exposition using basic mathematics)
• GHMM Library (home page of the GHMM Library project)
• Jahmm Java Library (Java library and associated graphical application)
• A step-by-step tutorial on HMMs (University of Leeds)
• Software for Markov Models and Processes (TreeAge Software)
• Hidden Markov Models (by Narada Warakagoda)