Catenoid

A catenoid

A catenoid obtained from the rotation of a catenary

A catenoid is a type of surface in topology, arising by rotating a catenary curve about an axis. It is a minimal surface, meaning that it occupies the least area when bounded by a closed space. It was formally described in 1744 by the mathematician Leonhard Euler.

Soap film attached to twin circular rings will take the shape of a catenoid. Because they are members of the same associate family of surfaces, a catenoid can be bent into a portion of a helicoid, and vice versa.

The dome shape of Inuit igloos can be derived from rotation of a catenary about its central axis.

Geometry

The catenoid was the first non-trivial minimal surface in 3-dimensional Euclidean space to be discovered apart from the plane. The catenoid is obtained by rotating a catenary about its directrix. It was found and proved to be minimal by Leonhard Euler in 1744.

Early work on the subject was published also by Jean Baptiste Meusnier. There are only two minimal surfaces of revolution (surfaces of revolution which are also minimal surfaces): the plane and the catenoid.

The catenoid may be defined by the following parametric equations:

$x=c\cosh {\frac {v}{c}}\cos u$

$y=c\cosh {\frac {v}{c}}\sin u$

$z=v$

where $u\in [-\pi ,\pi )$ and $v\in \mathbb {R}$ and $c$ is a non-zero real constant.

In cylindrical coordinates:

$\rho =c\cosh {\frac {z}{c}}$

where $c$ is a real constant.

A physical model of a catenoid can be formed by dipping two circular rings into a soap solution and slowly drawing the circles apart.

The catenoid may be also defined approximately by the Stretched grid method as a facet 3D model.

Helicoid transformation

Deformation of a helicoid into a catenoid

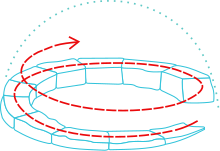
Because they are members of the same associate family of surfaces, one can bend a catenoid into a portion of a helicoid without stretching. In other words, one can make a (mostly) continuous and isometric deformation of a catenoid to a portion of the helicoid such that every member of the deformation family is minimal (having a mean curvature of zero). A parametrization of such a deformation is given by the system

$x(u,v)=\cos \theta \,\sinh v\,\sin u+\sin \theta \,\cosh v\,\cos u$

$y(u,v)=-\cos \theta \,\sinh v\,\cos u+\sin \theta \,\cosh v\,\sin u$

$z(u,v)=u\cos \theta +v\sin \theta$

for $(u,v)\in (-\pi ,\pi ]\times (-\infty ,\infty )$, with deformation parameter $-\pi <\theta \leq \pi$,

where $\theta =\pi$ corresponds to a right-handed helicoid, $\theta =\pm \pi /2$ corresponds to a catenoid, and $\theta =0$ corresponds to a left-handed helicoid.

Architecture

Further information: Igloo § Engineering

spiral sequence of snow blocks in igloo construction

The Inuit learned to pattern the structure of their igloos, or snow houses, after a shape with a catenary arch cross-section, which offers an optimal balance between height and diameter, avoiding the risk of collapsing under the weight of compacted snow. This differs from what is normally called a catenoid in that the catenary is rotated about its central axis, forming a surface with the topology of a bowl rather than that of a cylinder.

Further reading

• Krivoshapko, Sergey; Ivanov, V. N. (2015). "Minimal Surfaces". Encyclopedia of Analytical Surfaces. Springer. ISBN 9783319117737.

External links

• "Catenoid", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Catenoid - WebGL model
• Euler's text describing the catenoid at Carnegie Mellon University