Smoothsort: Difference between revisions
Banker's algorithm?, Dijkstra's algorithm?, Dijkstra-Scholten algorithm?, Dekker's algorithm?, Shunting-yard algorithm? [Category:Dutch inventions] |
→Overview: Rewrite overview to give a more conceptual view of the approach |
||
| Line 14: | Line 14: | ||
==Overview== |
==Overview== |
||
Like [[heapsort]], smoothsort first transforms the input array into an [[implicit data structure|implicit]] heap data structure, then produces the sorted array by repeatedly extracting the largest remaining element, whose location is determined by the heap structure, and the restoring the structure on the remaining elements. Whereas heapsort uses an implicit tree structure on the array in which a parent node always come before its descendants, so that the initial element is the root of the tree, smoothsort uses an implicit tree structure where a parent node always comes after its descendants. This has some important consequences, such as the fact that not all initial portions of the array correspond to a complete tree; however, it can help to avoid unnecessary displacements as in heapsort, where every element has to pass through the initial position (the root) just before getting swapped to its final position. Indeed, the algorithm is organized so that at the point where an element gets extracted from the heap structure, it is already at the rightmost position among the remaining elements, which is its proper place in the sorted array, so no swap is needed to bring it there. |
|||
Like [[heapsort]], smoothsort builds up an [[implicit data structure|implicit]] heap data structure in the array to be sorted, then sorts the array by repeatedly extracting the maximum element from that heap. Unlike heapsort, which places the root of the heap and largest element at the beginning (left) of the array before swapping it to the end (right), smoothsort places the root of the heap at the right, already in its final location. This, however, considerably complicates the algorithm for removing the rightmost element. |
|||
The tree structure defined on array positions is fixed and independent of the array contents. It can be extended to all natural numbers, and doing so there is no root, since every position gets to be a child of a parent further on; however some positions are leaves in an absolute sense. This contrasts with the tree structure used for heapsort, where the initial position is the global root, but there are no absolute leaves, since very position gets two children when sufficiently many positions are added. In the smoothsort structure, every position ''i'' is the root of a unique subtree, whose nodes form an interval that ends at ''i''. An initial interval of positions, and in particular the set of all positions in a given array, might be such an interval corresponding to a subtree, but in general decomposes as a union of a number of successive such subtree intervals, which Dijkstra calls "stretches". Any subtree rooted at a position whose parent lies beyond the initial interval considered gives a stretch in the decomposition of that interval, which decomposition is therefore unique. When a new position following the sequence of stretches is added, one of two things can be the case: either the position is a leaf and adds a stretch of length 1 to the decomposition, or it combines with the last two stretches, becoming the parent of their respective roots, thus replacing the two stretches by a new stretch containing their union plus the new (root) position. |
|||
Dijkstra's formulation of smoothsort does not use a [[binary heap]], but rather a custom heap based on the [[Leonardo numbers]]. As he pointed out in his original paper,<ref name=EWD-796a/> it is also possible to use perfect binary trees (of size 2<sup>''k''</sup>−1) with the same [[Asymptotic analysis|asymptotic efficiency]],{{r|hertel}} but there is a constant factor lost in efficiency due to the greater number of trees required by the larger spacing of permissible sizes. |
|||
Different rules could be used to determine for each position which of the two possibilities applies. For instance, one could stipulate that the last two stretches are combined if and only if they have equal size, in which case all subtrees would be perfect binary trees. Dijkstra's formulation of smoothsort uses a different rule, in which sibling subtrees never have equal sizes (except when both are 1), and the sizes of all subtrees are among a set of values that he calls [[Leonardo numbers]] (they are closely related to [[Fibonacci numbers]]). The general outline of the smoothsort procedure can be defined independently of the rule used to define the implicit tree structure, though the details of its steps depend on that rule. Dijkstra points out<ref name=EWD-796a/> that it would have been possible to use perfect binary trees (of size 2<sup>''k''</sup>−1); this would lead to the same [[Asymptotic analysis|asymptotic efficiency]],{{r|hertel}} but a constant factor in efficiency would be lost due to the on average greater number of stretches that a range of positions breaks up into. |
|||
The Leonardo numbers are similar to the [[Fibonacci numbers]], and defined as: |
|||
The rule Dijkstra uses is that the last two stretches are combined if and only if their sizes are ''successive'' Leonardo numbers L(i+1), L(i) (in decreasing order), which numbers are recursively defined as: |
|||
* L(0) = L(1) = 1 |
* L(0) = L(1) = 1 |
||
* L(k+2) = L(k+1) + L(k) + 1 |
* L(k+2) = L(k+1) + L(k) + 1 |
||
As a consequence, the size of any subtree is a Leonardo number. The sequence of sizes stretches decomposing the first ''n'' positions, for any ''n'', can be found in a greedy manner: the first size is the largest Leonardo number not exceeding ''n'', and the remainder (if any) is decomposed recursively. The sizes of stretches are decreasing, strictly so except possibly for two final sizes 1, and avoiding successive Leonardo numbers except possibly for the final two sizes. |
|||
In the initial phase of sorting, an increasingly large initial part of the array is reorganized so that the subtree for each of its stretches is a max-heap: the entry at any non-leaf position is at least as large as the entries at the positions that are its children. In addition, the subsequence of root (rightmost) entries of the stretches is kept increasing; this ensures in particular that the final root holds a maximal entry among the interval considered so far. In the second phase one shrinks the interval of interest back to smaller and smaller initial parts of the array, maintaining the same relations as before as the decomposition of the part considered into stretches evolves. At the point where a position disappears from the part under consideration due to shrinking, its entry is maximal among those in the part; as this is true at each shrinking step, those entries are left to sit in their proper position in the sorted result. |
|||
A Leonardo tree of order {{nobr|k ≥ 2}} is a [[binary tree]] with a root element, and two children which are themselves Leonardo trees, of orders k−1 and k−2. A Leonardo heap resembles a [[Fibonacci heap]] in that it is made up of a collection of [[Heap (data structure)|heap-ordered]] Leonardo trees. |
|||
Each tree is an implicit binary tree of size L(k), and the heap consists of a list of trees of decreasing size and increasing root elements. Ordered left-to-right, the rightmost tree is the smallest and its root element is the global maximum. |
|||
The advantage of this custom heap over a single binary heap is that if the input is already sorted, it can be constructed and deconstructed in {{math|O(''n'')}} time without moving any data, hence the better runtime. |
|||
Breaking the input up into a list of trees is simple – the leftmost nodes of the array are made into the largest tree possible, and the remainder is likewise divided up. The list is constructed to maintain the following size properties (it can be proven<ref>Schwartz, Keith (7 January 2011) [http://www.keithschwarz.com/smoothsort/ Smoothsort Demystified]. Keithschwarz.com. Retrieved on 2010-11-20.</ref> that this is always possible): |
|||
* No two trees have the same order. Except for L(1) = L(0), this means they will be different sizes. The list will therefore be a series of trees strictly decreasing in order. |
|||
* No two trees will have sizes that are consecutive Leonardo numbers, except for possibly the final two. |
|||
(In the perfect binary tree variant of smoothsort, the equivalent invariant is that no two trees have the ''same'' size, except possibly the last two. This is the [[skew binary number system]].) |
|||
An ''implicit'' Leonardo tree of order k and size L(k) is either a single node (for orders 0 and 1), or a left subtree of size {{nowrap|L(k − 1)}}, followed by a right subtree of size {{nowrap|L(k − 2)}}, followed by a root node. Each tree maintains the max-heap property that each node is always at least as large as either of its children (and thus the root of the tree is the largest element of all). The list of trees as a whole maintains the order property that the root node of each tree is at least as large as the root node of its predecessor (to the left). |
|||
The rearrangements necessary to ensure the required relations at all times, and thereby realize the eventual sorting of the array, are as follows. During the first "growing" phase, the heap relation must be enforced whenever two final stretches are combined with a new root to a single stretch; then (also in the case where a singleton stretch was added) the new root has to be compared to any previous roots of stretches to ensure that the subsequence remains increasing, basically by performing an insertion step on the subsequence by repeated swaps with predecessors; and finally, if the new root was moved backwards in this insertion, the max-heap property must be restored for the subtree where it ended (because the entry at the root position has decreased). During the "shrinking" phase, the only worry is keeping the subsequence of roots of stretches increasing as positions are added to and removed from the subsequence. This automatic whenever a stretch of length 1 is removed; however when a longer stretch breaks up and leaves two smaller stretches in its place, the values at their roots are unrelated to the entries at preceding roots, so preserving increase of the subsequence requires two insertion steps, each one (as before) followed by restoring the max-heap property in the stretch where the new entry ends up, unless it remained in its final position. |
|||
The consequence of this is that the root of the last (rightmost) tree in the list will always be the largest of the nodes, and, importantly, an array that is already sorted needs no rearrangement to be made into a valid Leonardo heap. This is the source of the adaptive qualities of the algorithm. |
|||
To this general plan, a few refinements are applied to arrive at Dijkstra's sorting procedure. Notably, in the growing phase, ensuring the max-heap property at the root of a newly formed stretch can be combined with ordering it relative to the root of the preceding stretch: if the latter is larger than the new root, then either it also dominates both children of the new root, in which case swapping the roots also repairs the max-heap property, or else swapping the new root with its larger child also repairs the relation with the previous stretch root (but the repair of the max-heap property still needs to propagate down the heap). All in all, at most one series of swaps needs to propagate through the structure during each growing step; by contrast, a shrinking step may as mentioned involve either no such series or two of them. |
|||
Like heapsort, the algorithm consists of two phases. In the first, the heap is grown by repeatedly adding the next unsorted element, and performing rearrangements to restore the heap properties. |
|||
Implementation of the implicit tree structures could be easily done by computing once and for all a list of Leonardo numbers and tables for parent and child relations (which do not depend at all on the values to be sorted). But in order to make this qualify as an in-place sorting algorithm, Dijkstra maintains in a slick way a fixed number of integer variables in such a way that at each point in the computation gives access to the relevant information, without requiring any tables. While doing so does not affect complexity, it does take up a large part of the code for the algorithm, and makes the latter more difficult to understand. |
|||
In phase two, the root of the last tree in the list will be the largest element in the heap, and will therefore be in its correct, final position. We then reduce the series of heaps back down by removing the rightmost node (which stays in place) and performing re-arrangements to restore the heap invariants. When we are back down to a single heap of one element, the array is sorted. |
|||
==Operations== |
==Operations== |
||
Revision as of 08:09, 18 July 2018
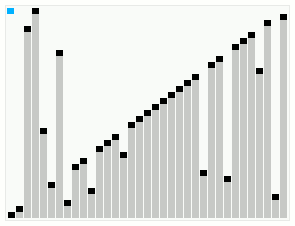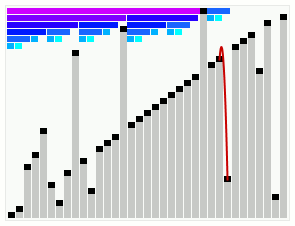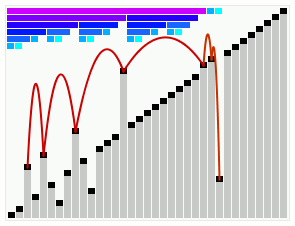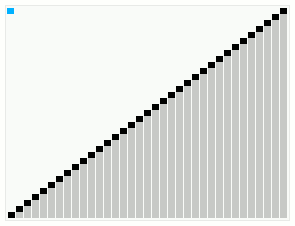 Smoothsort operating on an array which is mostly in order. The bars across the top show the tree structure. | |
| Class | Sorting algorithm |
|---|---|
| Data structure | Array |
| Worst-case performance | O(n log n) |
| Best-case performance | O(n) |
| Average performance | O(n log n) |
| Worst-case space complexity | O(n) total, O(1) auxiliary |
| Optimal | When the data is already sorted |
In computer science, smoothsort is a comparison-based sorting algorithm. A variant of heapsort, it was invented and published by Edsger Dijkstra in 1981.[1] Like heapsort, smoothsort is an in-place algorithm with an upper bound of O(n log n),[2] but it is not a stable sort.[3][self-published source?] The advantage of smoothsort is that it comes closer to O(n) time if the input is already sorted to some degree, whereas heapsort averages O(n log n) regardless of the initial sorted state.
Overview
Like heapsort, smoothsort first transforms the input array into an implicit heap data structure, then produces the sorted array by repeatedly extracting the largest remaining element, whose location is determined by the heap structure, and the restoring the structure on the remaining elements. Whereas heapsort uses an implicit tree structure on the array in which a parent node always come before its descendants, so that the initial element is the root of the tree, smoothsort uses an implicit tree structure where a parent node always comes after its descendants. This has some important consequences, such as the fact that not all initial portions of the array correspond to a complete tree; however, it can help to avoid unnecessary displacements as in heapsort, where every element has to pass through the initial position (the root) just before getting swapped to its final position. Indeed, the algorithm is organized so that at the point where an element gets extracted from the heap structure, it is already at the rightmost position among the remaining elements, which is its proper place in the sorted array, so no swap is needed to bring it there.
The tree structure defined on array positions is fixed and independent of the array contents. It can be extended to all natural numbers, and doing so there is no root, since every position gets to be a child of a parent further on; however some positions are leaves in an absolute sense. This contrasts with the tree structure used for heapsort, where the initial position is the global root, but there are no absolute leaves, since very position gets two children when sufficiently many positions are added. In the smoothsort structure, every position i is the root of a unique subtree, whose nodes form an interval that ends at i. An initial interval of positions, and in particular the set of all positions in a given array, might be such an interval corresponding to a subtree, but in general decomposes as a union of a number of successive such subtree intervals, which Dijkstra calls "stretches". Any subtree rooted at a position whose parent lies beyond the initial interval considered gives a stretch in the decomposition of that interval, which decomposition is therefore unique. When a new position following the sequence of stretches is added, one of two things can be the case: either the position is a leaf and adds a stretch of length 1 to the decomposition, or it combines with the last two stretches, becoming the parent of their respective roots, thus replacing the two stretches by a new stretch containing their union plus the new (root) position.
Different rules could be used to determine for each position which of the two possibilities applies. For instance, one could stipulate that the last two stretches are combined if and only if they have equal size, in which case all subtrees would be perfect binary trees. Dijkstra's formulation of smoothsort uses a different rule, in which sibling subtrees never have equal sizes (except when both are 1), and the sizes of all subtrees are among a set of values that he calls Leonardo numbers (they are closely related to Fibonacci numbers). The general outline of the smoothsort procedure can be defined independently of the rule used to define the implicit tree structure, though the details of its steps depend on that rule. Dijkstra points out[1] that it would have been possible to use perfect binary trees (of size 2k−1); this would lead to the same asymptotic efficiency,[2] but a constant factor in efficiency would be lost due to the on average greater number of stretches that a range of positions breaks up into.
The rule Dijkstra uses is that the last two stretches are combined if and only if their sizes are successive Leonardo numbers L(i+1), L(i) (in decreasing order), which numbers are recursively defined as:
- L(0) = L(1) = 1
- L(k+2) = L(k+1) + L(k) + 1
As a consequence, the size of any subtree is a Leonardo number. The sequence of sizes stretches decomposing the first n positions, for any n, can be found in a greedy manner: the first size is the largest Leonardo number not exceeding n, and the remainder (if any) is decomposed recursively. The sizes of stretches are decreasing, strictly so except possibly for two final sizes 1, and avoiding successive Leonardo numbers except possibly for the final two sizes.
In the initial phase of sorting, an increasingly large initial part of the array is reorganized so that the subtree for each of its stretches is a max-heap: the entry at any non-leaf position is at least as large as the entries at the positions that are its children. In addition, the subsequence of root (rightmost) entries of the stretches is kept increasing; this ensures in particular that the final root holds a maximal entry among the interval considered so far. In the second phase one shrinks the interval of interest back to smaller and smaller initial parts of the array, maintaining the same relations as before as the decomposition of the part considered into stretches evolves. At the point where a position disappears from the part under consideration due to shrinking, its entry is maximal among those in the part; as this is true at each shrinking step, those entries are left to sit in their proper position in the sorted result.
The rearrangements necessary to ensure the required relations at all times, and thereby realize the eventual sorting of the array, are as follows. During the first "growing" phase, the heap relation must be enforced whenever two final stretches are combined with a new root to a single stretch; then (also in the case where a singleton stretch was added) the new root has to be compared to any previous roots of stretches to ensure that the subsequence remains increasing, basically by performing an insertion step on the subsequence by repeated swaps with predecessors; and finally, if the new root was moved backwards in this insertion, the max-heap property must be restored for the subtree where it ended (because the entry at the root position has decreased). During the "shrinking" phase, the only worry is keeping the subsequence of roots of stretches increasing as positions are added to and removed from the subsequence. This automatic whenever a stretch of length 1 is removed; however when a longer stretch breaks up and leaves two smaller stretches in its place, the values at their roots are unrelated to the entries at preceding roots, so preserving increase of the subsequence requires two insertion steps, each one (as before) followed by restoring the max-heap property in the stretch where the new entry ends up, unless it remained in its final position.
To this general plan, a few refinements are applied to arrive at Dijkstra's sorting procedure. Notably, in the growing phase, ensuring the max-heap property at the root of a newly formed stretch can be combined with ordering it relative to the root of the preceding stretch: if the latter is larger than the new root, then either it also dominates both children of the new root, in which case swapping the roots also repairs the max-heap property, or else swapping the new root with its larger child also repairs the relation with the previous stretch root (but the repair of the max-heap property still needs to propagate down the heap). All in all, at most one series of swaps needs to propagate through the structure during each growing step; by contrast, a shrinking step may as mentioned involve either no such series or two of them.
Implementation of the implicit tree structures could be easily done by computing once and for all a list of Leonardo numbers and tables for parent and child relations (which do not depend at all on the values to be sorted). But in order to make this qualify as an in-place sorting algorithm, Dijkstra maintains in a slick way a fixed number of integer variables in such a way that at each point in the computation gives access to the relevant information, without requiring any tables. While doing so does not affect complexity, it does take up a large part of the code for the algorithm, and makes the latter more difficult to understand.
Operations
Ignoring (for the moment) Dijkstra's optimisations, two operations are necessary: enlarge the heap by adding one element to the right, and shrink the heap by removing the right most element (the root of the last heap), preserving the three types of invariant properties:
- The heap property within each tree,
- The order property, keeping the root elements of the trees in order, and
- The size properties relating the sizes of the various trees.
Grow the heap by adding an element to the right
Enlarging the heap while maintaining the size properties can be done without any data motion at all by just rearranging the boundaries of the component trees:
- If the last two trees are of size L(k+1) and L(k) (i.e., consecutive Leonardo numbers), combine them with the new element as the root of a larger tree of size L(k+2). Because consecutive trees other than the last two may not have consecutive orders, the third-last tree must have been of size at least L(k+3), and therefore the size property is maintained. This new tree will probably not have the heap property.
- If the last two trees in the list are not consecutive Leonardo numbers, then we may simply add a new heap of size 1 to the list. This 1 is taken to be L(1), unless the rightmost tree is already of order 1, in which case the new one-element tree is taken to be of size L(0).
After this, the newly added element must be moved to the correct location to maintain the heap and order properties. Because there are O(log n) trees, each of depth O(log n), it is simple to do this in O(log n) time, as follows:
- First, restore the order property by moving the new element left until it is at the root of the correct tree:
- Begin with the rightmost tree (the one that has just been created) as the "current" tree.
- While there is a tree to the left of the current tree and its root is greater than the new element (the current root) and both of its children,
- swap the new element with the root of the tree to the left. This preserves the heap property of the current tree. The tree on the left then becomes the current tree, and we repeat this step.
- Second, restore the heap property to the current tree by "sifting down" the new element to its correct position. (This is a standard heap operation, as used in heapsort.)
- While the current tree has a size greater than 1 and either child of is greater than the current root, then
- Swap the greater child root with the current root. That child tree becomes the current tree and sift-down continues.
- While the current tree has a size greater than 1 and either child of is greater than the current root, then
The sift-down operation is slightly simpler than in binary heaps, because each node has either two children or zero. One does not need to handle the condition of one of the child heaps not being present.
Optimisation
There are two opportunities to omit some operations during heap construction:
- If the new tree is going to become part of a larger tree before we are done, then don't bother establishing the order property: it only needs to be done when a tree has reached its final size.
- To do this, look at how many elements remain after the new tree of size L(k). If there are L(k − 1) + 1 or more, then this new tree is going to be merged.
- Do not maintain the heap property of the rightmost tree. If that tree becomes one of the final trees of the heap, then maintaining the order property will restore the heap property. Of course, whenever a new tree is added to the list, then the rightmost tree is no longer the rightmost and the heap property needs to be restored, but this can be done in O(n) time, whereas maintaining it at each step takes O(n log n) time.
Shrink the heap by removing the rightmost element
This is the reverse of the grow process:
- If the rightmost tree has a size of 1 (i.e., L(1) or L(0)), then this is trivial; simply remove that rightmost tree.
- If the rightmost tree has size greater than 1, then remove its root, exposing the two sub-trees as members of the list. This preserves the size property. Restore the order property using the same algorithm as in construction; first on the left subtree, and then on the right one.
Optimisation
- Unlike when constructing the heap, when restoring the order property after removing a tree's root, we know that the newly exposed trees satisfy the heap property. Therefore, it is not necessary to compare the preceding tree's root to the children of the newly exposed root. Just compare it to the root. (This only applies to the first step. After an element has been swapped left once, it is necessary to compare to both children.)
Analysis
Smoothsort takes O(n) time to process a presorted array and O(n log n) in the worst case, and achieves nearly-linear performance on many nearly-sorted inputs. However, it does not handle all nearly-sorted sequences optimally. Using the count of inversions as a measure of un-sortedness (the number of pairs of indices i and j with i < j and A[i] > A[j]; for randomly sorted input this is approximately n2/4), there are possible input sequences with O(n log n) inversions which cause it to take Ω(n log n) time, whereas other adaptive sorting algorithms can solve these cases in O(n log log n) time.[2]
The smoothsort algorithm needs to be able to hold in memory the sizes of all of the trees in the Leonardo heap. Since they are sorted by order and all orders are distinct, this is usually done using a bit vector indicating which orders are present. Moreover, since the largest order is at most O(log n), these bits can be encoded in O(1) machine words, assuming a transdichotomous machine model.
Note that O(1) machine words is not the same thing as one machine word. A 32-bit vector would only suffice for sizes less than L(32) = 7049155. A 64-bit vector will do for sizes less than L(64) = 34335360355129 ≈ 245. In general, it takes 1/log2(φ) ≈ 1.44 bits of vector per bit of size.
References
- ^ a b Dijkstra, Edsger W. Smoothsort – an alternative to sorting in situ (EWD-796a) (PDF). E.W. Dijkstra Archive. Center for American History, University of Texas at Austin.
One can also raise the question why I have not chosen as available stretch lengths: ... 63 31 15 7 3 1 which seems attractive since each stretch can then be viewed as the postorder traversal of a balanced binary tree. In addition, the recurrence relation would be simpler. But I know why I chose the Leonardo numbers:
(transcription) - ^ a b c Hertel, Stefan (13 May 1983). "Smoothsort's behavior on presorted sequences" (PDF). Information Processing Letters. 16 (4): 165–170. doi:10.1016/0020-0190(83)90116-3.
- ^ Brown, Craig (21 Jan 2013). "Fastest In-Place Stable Sort". Code Project.

