Semi-log plot

The log-lin type of a semi-log graph, defined by a logarithmic scale on the y-axis, and a linear scale on the x-axis. Plotted lines are: y = 10^x (red), y = x (green), y = log(x) (blue).

The lin-log type of a semi-log graph, defined by a logarithmic scale on the x axis, and a linear scale on the y axis. Plotted lines are: y = 10^x (red), y = x (green), y = log(x) (blue).

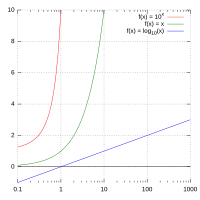
In science and engineering, a semi-log graph or semi-log plot is a way of visualizing data that are related according to an exponential relationship. One axis is plotted on a logarithmic scale.

This kind of plotting method is useful when one of the variables being plotted covers a large range of values and the other has only a restricted range – the advantage being that it can bring out features in the data that would not easily be seen if both variables had been plotted linearly.

All equations of the form $y=\lambda a^{\gamma x}$ form straight lines when plotted semi-logarithmically, since taking logs of both sides gives

$\log _{a}y=\gamma x+\log _{a}\lambda .$

This can easily be seen as a line in slope-intercept form with $\gamma$ as the slope and $\log _{a}\lambda$ as the vertical intercept. To facilitate use with logarithmic tables, one usually takes logs to base 10 or e, or sometimes base 2:

$\log(y)=(\gamma \log(a))x+\log(\lambda ).$

The term log-lin is used to describe a semi-log plot with a logarithmic scale on the y-axis, and a linear scale on the x-axis. Likewise, a lin-log plot uses a logarithmic scale on the x-axis, and a linear scale on the y-axis. Note that the naming is output-input (y-x), the opposite order from (x, y).

On a semi-log plot the spacing of the scale on the y-axis (or x-axis) is proportional to the logarithm of the number, not the number itself. It is equivalent to converting the y values (or x values) to their log, and plotting the data on lin-lin scales. A log-log plot uses the logarithmic scale for both axes, and hence is not a semi-log plot.

Equations

The equation for a line with an ordinate axis logarithmically scaled would be:

$\log _{10}(F(x))=mx+b$

$F(x)=10^{mx+b}=(10^{mx})(10^{b}).$

The equation of a line on a plot where the abscissa axis is scaled logarithmically would be

$F(x)=m\log _{10}(x)+b.\,$

Real-world examples

Phase diagram of water

In physics and chemistry, a plot of logarithm of pressure against temperature can be used to illustrate the various phases of a substance, as in the following for water:

Log-lin pressure–temperature phase diagram of water. The Roman numerals indicate various ice phases.

2009 "swine flu" progression

While ten is the most common base, there are times when other bases are more appropriate, as in this example:

A semi-logarithmic plot of cases and deaths in the 2009 outbreak of influenza A (H1N1). Notice that while the horizontal (time) axis is linear, with the dates evenly spaced, the vertical (cases) axis is logarithmic, with the evenly spaced divisions being labelled with successive powers of two.

Microbial growth

In biology and biological engineering, the change in numbers of microbes due to asexual reproduction and nutrient exhaustion is commonly illustrated by a semi-log plot. Time is usually the independent axis, with the logarithm of the number or mass of bacteria or other microbe as the dependent variable. This forms a plot with four distinct phases, as shown below.

Bacterial growth curve

See also

• Multiplicative calculus
• Nomograph, more complicated graphs
• Nonlinear regression#Transformation, for converting a nonlinear form to a semi-log form amenable to non-iterative calculation