Disjoint union (topology)

In general topology and related areas of mathematics, the disjoint union (also called the direct sum, free union, free sum, topological sum, or coproduct) of a family of topological spaces is a space formed by equipping the disjoint union of the underlying sets with a natural topology called the disjoint union topology. Roughly speaking, two or more spaces may be considered together, each looking as it would alone.

The name coproduct originates from the fact that the disjoint union is the categorical dual of the product space construction.

Definition

Let {X_i : i ∈ I} be a family of topological spaces indexed by I. Let

$X=\coprod _{i}X_{i}$

be the disjoint union of the underlying sets. For each i in I, let

$\varphi _{i}:X_{i}\to X\,$

be the canonical injection (defined by $\varphi _{i}(x)=(x,i)$). The disjoint union topology on X is defined as the finest topology on X for which all the canonical injections $\varphi _{i}$ are continuous.

Explicitly, the disjoint union topology can be described as follows. A subset U of X is open in X if and only if its preimage $\varphi _{i}^{-1}(U)$ is open in X_i for each i ∈ I. Yet another formulation is that a subset V of X is open relative to X iff its intersection with X_i is open relative to X_i for each i.

Properties

The disjoint union space X, together with the canonical injections, can be characterized by the following universal property: If Y is a topological space, and f_i : X_i → Y is a continuous map for each i ∈ I, then there exists precisely one continuous map f : X → Y such that the following set of diagrams commute:

Characteristic property of disjoint unions

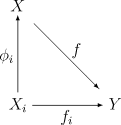
This shows that the disjoint union is the coproduct in the category of topological spaces. It follows from the above universal property that a map f : X → Y is continuous iff f_i = f o φ_i is continuous for all i in I.

In addition to being continuous, the canonical injections φ_i : X_i → X are open and closed maps. It follows that the injections are topological embeddings so that each X_i may be canonically thought of as a subspace of X.

Examples

If each X_i is homeomorphic to a fixed space A, then the disjoint union X will be homeomorphic to A × I where I is the discrete topology.

Preservation of topological properties

• Every disjoint union of discrete spaces is discrete
• Separation
  • Every disjoint union of T₀ spaces is T₀
  • Every disjoint union of T₁ spaces is T₁
  • Every disjoint union of Hausdorff spaces is Hausdorff
• Connectedness
  • The disjoint union of two or more nonempty topological spaces is disconnected

See also

• product topology, the dual construction
• subspace topology and its dual quotient topology
• topological union, a generalization to the case where the pieces are not disjoint