Minesweeper (video game)

This article is about the Minesweeper game as a whole. For the Microsoft version, see Microsoft Minesweeper. For other uses, see Minesweeper (disambiguation).

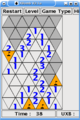
Minesweeper is a single-player puzzle video game. The objective of the game is to clear a rectangular board containing hidden "mines" or bombs without detonating any of them, with help from clues about the number of neighboring mines in each field. The game originates from the 1960s, and has been written for many computing platforms in use today. It has many variations and offshoots.

Some versions of Minesweeper will set up the board by never placing a mine on the first square revealed. Minesweeper for versions of Windows protects the first square revealed; from Windows 7 onward, players may elect to replay a board, in which the game is played by revealing squares of the grid by clicking or otherwise indicating each square. If a square containing a mine is revealed, the player loses the game. If no mine is revealed, a digit is instead displayed in the square, indicating how many adjacent squares contain mines; if no mines are adjacent, the square becomes blank, and all adjacent squares will be recursively revealed. The player uses this information to deduce the contents of other squares, and may either safely reveal each square or mark the square as containing a mine.

History

Minesweeper has its origins in the earliest mainframe games of the 1960s and 1970s. The earliest ancestor of Minesweeper was Jerimac Ratliff's Cube. The basic gameplay style became a popular segment of the puzzle video game genre during the 1980s, with such titles as Mined-Out (Quicksilva, 1983), Yomp (Virgin Interactive, 1983), and Cube. Cube was succeeded by Relentless Logic (or RLogic for short), by Conway, Hong, and Smith, available for MS-DOS as early as 1985; the player took the role of a private in the United States Marine Corps, delivering an important message to the U.S. Command Center. RLogic had greater similarity to Minesweeper than to Cube in concept, but a number of differences exist:

• In RLogic, the player must navigate through the minefield, from the top left right angled corner to the bottom right angled corner (the Command Center).
• It is not necessary to clear all non-mine squares. Also, there is no mechanism for marking mines or counting the number of mines found.
• The number of steps taken is counted. Although no high score functionality is included, players could attempt to beat their personal best score for a given number of mines.
• Unlike Minesweeper, the size of the minefield is fixed. However, the player may still specify the number of mines.
• Because the player must navigate through the minefield, it is sometimes impossible to win — namely, when the mines block all possible paths.

The gameplay mechanics of Minesweeper are included in a variety of other software titles, including:

• The mini-game Vinesweeper implemented into the MMORPG RuneScape; in this iteration (written by Jagex developer Danny J), the Minesweeper gameplay is given a large multiplayer aspect and the "game board" adopts a continually resetting timer. This allows for a never-ending game of Minesweeper where the skill is assessed in points rather than "game completion".
• The PC game Mole Control (developed by Remode); in this game, the Minesweeper mechanic is integrated into a puzzle adventure game based in a village called Molar Creek, which has been overrun with exploding moles. The player acts as the local inventor's assistant, who is tasked with clearing the village of exploding moles. A time attack mode, called the Molar Creek Annual Mole Control competition, is also available.

Distribution and variants

Versions of Minesweeper are frequently bundled with operating systems and GUIs, including Minesweeper for OS/2, Minesweeper in Windows, KMines in KDE (Unix-like OSes), GNOME Mines in GNOME and MineHunt in Palm OS. Many clones can be found on the Internet.

Variants of the basic game generally have differently shaped minefields, in either two and eight dimensions, and may have more than one mine per cell. For example, X11-based XBomb adds triangular and hexagonal grids, and Professional Minesweeper for Windows includes these and others. There are also variants for more than one player, in which the players compete against each other.

The HP-48G graphing calculator includes a variation on the theme called "Minehunt", where the player has to move safely from one corner of the playfield to the other. The only clues given are how many mines are in the squares surrounding the player's current position.

The Voltorb Flip game in the non-Japanese releases of Pokémon HeartGold and SoulSilver is a variation of Minesweeper and Picross.

A tentaizu puzzle with three stars (mines) already located and four remaining to be found.

A logic puzzle variant of minesweeper, suitable for playing on paper, starts with some squares already revealed. The player cannot reveal any more squares, but must instead mark the remaining mines correctly. Unlike the usual form of minesweeper, these puzzles usually have a unique solution. These puzzles appeared under the name "tentaizu", Japanese for a star map, in Southwest Airlines' magazine Spirit in 2008–2009.

In the game Minecraft, the 2015 April Fool's update "The Love and Hugs Update" added "Minescreeper". It is a near exact copy of Minesweeper, except, instead of avoiding the mines, the player must avoid hidden Creepers.

• 
  Online, non rectangular
• 
  3D
• 
  Hexagonal
• 
  Triangular
• 
  Multiple mines in cells

Computational complexity

In 2000, Richard Kaye published a proof that it is NP-complete to determine whether a given grid of uncovered, correctly flagged, and unknown squares, the labels of the foremost also given, has an arrangement of mines for which it is possible within the rules of the game. The argument is constructive, a method to quickly convert any Boolean circuit into such a grid that is possible if and only if the circuit is satisfiable; membership in NP is established by using the arrangement of mines as a certificate. If, however, a minesweeper board is already guaranteed to be consistent, solving it is not known to be NP-complete, but it has been proven to be co-NP-complete.

Kaye also proved that infinite Minesweeper is Turing complete.

Rules

The first click will never be a mine this is all fake . It will clear the map and place numbers on the grid. The numbers reflect the number of mines touching a square.

See also

• Board puzzles with algebra of binary variables

References

• Adamatzky, Andrew (1997). "How cellular automaton plays Minesweeper". Applied Mathematics and Computation. 85 (2–3): 127–137. doi:10.1016/S0096-3003(96)00117-8.
• Lakshtanov, Evgeny; Oleg German (2010). "'Minesweeper' and spectrum of discrete Laplacians". Applicable Analysis. 89 (12): 1907–1916. arXiv:0806.3480. doi:10.1080/00036811.2010.505189.
• Kaye, Richard (2000). "Minesweeper is NP-complete". Mathematical Intelligencer. 22 (2): 9–15. doi:10.1007/BF03025367. — Further information available online at Richard Kaye's Minesweeper pages.
• Mordechai Ben-Ari (2018). Minesweeper is NP-Complete (PDF) (Report). Weizmann Institute of Science, Department of Science Teaching. — An open-access paper explaining Kaye's NP-completeness result.