Cubitruncated cuboctahedron: Difference between revisions
Content deleted Content added
OfficialURL (talk | contribs) Added 3D model |
OfficialURL (talk | contribs) mNo edit summary |
||
| Line 1: | Line 1: | ||
{{Uniform polyhedra db|Uniform polyhedron stat table|ctCO}} |
{{Uniform polyhedra db|Uniform polyhedron stat table|ctCO}} |
||
[[File:Cubitruncated cuboctahedron (STL).stl|thumb|3D model of a cubitruncated cuboctahedron]] |
[[File:Cubitruncated cuboctahedron (STL).stl|thumb|3D model of a cubitruncated cuboctahedron]] |
||
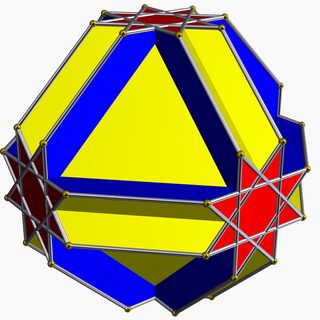
In [[geometry]], the '''cubitruncated cuboctahedron''' or '''cuboctatruncated cuboctahedron''' is a [[nonconvex uniform polyhedron]], indexed as U<sub>16</sub>. It has 20 faces, 72 edges, and 48 vertices.<ref>{{Cite web|url=https://www.mathconsult.ch/enwiki/static/unipoly/16.html|title=16: cubitruncated cuboctahedron|last=Maeder|first=Roman|date=|website=MathConsult|url-status=live|archive-url=|archive-date=|access-date=}}</ref> |
In [[geometry]], the '''cubitruncated cuboctahedron''' or '''cuboctatruncated cuboctahedron''' is a [[nonconvex uniform polyhedron]], indexed as U<sub>16</sub>. It has 20 faces (8 [[Hexagon|hexagons]], 6 [[Octagon|octagons]], and 6 [[Octagram|octagrams]]), 72 edges, and 48 vertices.<ref>{{Cite web|url=https://www.mathconsult.ch/enwiki/static/unipoly/16.html|title=16: cubitruncated cuboctahedron|last=Maeder|first=Roman|date=|website=MathConsult|url-status=live|archive-url=|archive-date=|access-date=}}</ref> |
||
== Convex hull == |
== Convex hull == |
||
Revision as of 03:50, 9 April 2020
| Cubitruncated cuboctahedron | |
|---|---|
| |
| Type | Uniform star polyhedron |
| Elements | F = 20, E = 72 V = 48 (χ = −4) |
| Faces by sides | 8{6}+6{8}+6{8/3} |
| Coxeter diagram |    
|
| Wythoff symbol | 3 4 4/3 | |
| Symmetry group | Oh, [4,3], *432 |
| Index references | U16, C52, W79 |
| Dual polyhedron | Tetradyakis hexahedron |
| Vertex figure |  6.8.8/3 |
| Bowers acronym | Cotco |
In geometry, the cubitruncated cuboctahedron or cuboctatruncated cuboctahedron is a nonconvex uniform polyhedron, indexed as U16. It has 20 faces (8 hexagons, 6 octagons, and 6 octagrams), 72 edges, and 48 vertices.[1]
Convex hull
Its convex hull is a nonuniform truncated cuboctahedron.
 Convex hull |
Cubitruncated cuboctahedron |
Orthogonal projection
Cartesian coordinates
Cartesian coordinates for the vertices of a cubitruncated cuboctahedron are all the permutations of
- (±(√2−1), ±1, ±(√2+1))
Related polyhedra
Tetradyakis hexahedron
| Tetradyakis hexahedron | |
|---|---|
| |
| Type | Star polyhedron |
| Face | 
|
| Elements | F = 48, E = 72 V = 20 (χ = −4) |
| Symmetry group | Oh, [4,3], *432 |
| Index references | DU16 |
| dual polyhedron | Cubitruncated cuboctahedron |
The tetradyakis hexahedron (or great disdyakis dodecahedron) is a nonconvex isohedral polyhedron. It has 48 intersecting scalene triangle faces, 72 edges, and 20 vertices.
It is the dual of the uniform cubitruncated cuboctahedron.
See also
References
- ^ Maeder, Roman. "16: cubitruncated cuboctahedron". MathConsult.
{{cite web}}: CS1 maint: url-status (link)
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 0730208 p. 92
External links
- Weisstein, Eric W. "Cubitruncated cuboctahedron". MathWorld.
- Weisstein, Eric W. "Tetradyakis hexahedron". MathWorld.
- http://gratrix.net Uniform polyhedra and duals
 | This polyhedron-related article is a stub. You can help Wikipedia by expanding it. |