Nerve complex: Difference between revisions
Erel Segal (talk | contribs) |
Citation bot (talk | contribs) Add: isbn, volume, doi, s2cid, author pars. 1-1. Removed URL that duplicated unique identifier. Removed parameters. Some additions/deletions were actually parameter name changes. | You can use this bot yourself. Report bugs here. | Suggested by AManWithNoPlan | All pages linked from cached copy of User:AManWithNoPlan/sandbox2 | via #UCB_webform_linked |
||
| Line 1: | Line 1: | ||
[[File:Constructing nerve.png|thumb|Constructing the nerve of an open good cover containing 3 sets in the plane.]] |
[[File:Constructing nerve.png|thumb|Constructing the nerve of an open good cover containing 3 sets in the plane.]] |
||
In [[topology]], the '''nerve of an open covering''' is a construction of an [[abstract simplicial complex]] from an [[Cover (topology)#open cover|open covering]] of a [[topological space]] ''X'' that captures many of the interesting topological properties in an algorithmic or combinatorial way. It was introduced by [[Pavel Alexandrov]]<ref>{{cite journal|last=Aleksandroff|first=P. S.|author-link=Pavel Alexandrov| title=Über den allgemeinen Dimensionsbegriff und seine Beziehungen zur elementaren geometrischen Anschauung |journal=[[Mathematische Annalen]]|volume=98 |year=1928| pages=617–635|doi= 10.1007/BF01451612}}</ref> and now has many variants and generalisations, among them the '''Čech nerve''' of a cover, which in turn is generalised by [[hypercovering|hypercoverings]].<ref>{{Cite book| |
In [[topology]], the '''nerve of an open covering''' is a construction of an [[abstract simplicial complex]] from an [[Cover (topology)#open cover|open covering]] of a [[topological space]] ''X'' that captures many of the interesting topological properties in an algorithmic or combinatorial way. It was introduced by [[Pavel Alexandrov]]<ref>{{cite journal|last=Aleksandroff|first=P. S.|author-link=Pavel Alexandrov| title=Über den allgemeinen Dimensionsbegriff und seine Beziehungen zur elementaren geometrischen Anschauung |journal=[[Mathematische Annalen]]|volume=98 |year=1928| pages=617–635|doi= 10.1007/BF01451612|s2cid=119590045}}</ref> and now has many variants and generalisations, among them the '''Čech nerve''' of a cover, which in turn is generalised by [[hypercovering|hypercoverings]].<ref>{{Cite book|last1=Eilenberg|first1=Samuel|title=Foundations of Algebraic Topology|last2=Steenrod|first2=Norman|date=1952-12-31|publisher=Princeton University Press|isbn=978-1-4008-7749-2|location=Princeton|doi=10.1515/9781400877492}}</ref> |
||
==Alexandrov's definition== |
==Alexandrov's definition== |
||
Let ''X'' be a topological space. Let ''<math>I</math>'' be an [[index set]]. Let ''<math>C</math>'' be a family indexed by ''<math>I</math>'' of [[Open set|open subsets]] of ''X'': <math>C = \lbrace U_i: i \in I\rbrace</math>. The '''nerve''' of ''<math>C</math>'' is a set of finite subsets of the index-set ''<math>I</math>''. It contains all finite subsets ''<math>J\subseteq I</math>'' such that the intersection of the ''U<sub>i</sub>'' whose subindices are in ''J'' is non-empty: |
Let ''X'' be a topological space. Let ''<math>I</math>'' be an [[index set]]. Let ''<math>C</math>'' be a family indexed by ''<math>I</math>'' of [[Open set|open subsets]] of ''X'': <math>C = \lbrace U_i: i \in I\rbrace</math>. The '''nerve''' of ''<math>C</math>'' is a set of finite subsets of the index-set ''<math>I</math>''. It contains all finite subsets ''<math>J\subseteq I</math>'' such that the intersection of the ''U<sub>i</sub>'' whose subindices are in ''J'' is non-empty: |
||
| Line 24: | Line 24: | ||
However, in some cases N(''C'') does reflect the topology of ''X''. For example, if a circle is covered by three open arcs, intersecting in pairs as in example 2 above, then N(''C'') is a 2-simplex (without its interior) and it is [[homotopy-equivalent]] to the original circle. |
However, in some cases N(''C'') does reflect the topology of ''X''. For example, if a circle is covered by three open arcs, intersecting in pairs as in example 2 above, then N(''C'') is a 2-simplex (without its interior) and it is [[homotopy-equivalent]] to the original circle. |
||
<ref>{{Cite journal| |
<ref>{{Cite journal|last1=Artin|first1=M.|last2=Mazur|first2=B.|date=1969|title=Etale Homotopy|journal=Lecture Notes in Mathematics|volume=100|doi=10.1007/bfb0080957|isbn=978-3-540-04619-6|issn=0075-8434}}</ref> |
||
A '''nerve theorem''' (or '''nerve lemma''') is a theorem that gives sufficient conditions on ''C'' guaranteeing that N(''C'') reflects, in some sense, the topology of ''X''. |
A '''nerve theorem''' (or '''nerve lemma''') is a theorem that gives sufficient conditions on ''C'' guaranteeing that N(''C'') reflects, in some sense, the topology of ''X''. |
||
| Line 33: | Line 33: | ||
=== Homological nerve theorem === |
=== Homological nerve theorem === |
||
The following nerve theorem uses the [[homology groups]] of intersections of sets in the cover.<ref name=":3">{{Cite journal|last=Meshulam|first=Roy|date=2001-01-01|title=The Clique Complex and Hypergraph Matching |
The following nerve theorem uses the [[homology groups]] of intersections of sets in the cover.<ref name=":3">{{Cite journal|last=Meshulam|first=Roy|date=2001-01-01|title=The Clique Complex and Hypergraph Matching|journal=Combinatorica|language=en|volume=21|issue=1|pages=89–94|doi=10.1007/s004930170006|s2cid=207006642|issn=1439-6912}}</ref> For each finite <math>J\subset I</math>, denote <math>H_{J,j} := \tilde{H}_j(\bigcap_{i\in J} U_i)=</math> the ''j''-th [[reduced homology]] group of <math>\bigcap_{i\in J} U_i</math>. |
||
If ''H<sub>J,j</sub>'' is the [[trivial group]] for all ''J'' in the ''k''-skeleton of N(''C'') and for all ''j'' in {0, ..., ''k''-dim(''J'')}, then N(''C'') is "homology-equivalent" to ''X'' in the following sense: |
If ''H<sub>J,j</sub>'' is the [[trivial group]] for all ''J'' in the ''k''-skeleton of N(''C'') and for all ''j'' in {0, ..., ''k''-dim(''J'')}, then N(''C'') is "homology-equivalent" to ''X'' in the following sense: |
||
Revision as of 16:43, 4 September 2020
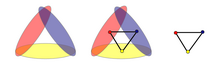
In topology, the nerve of an open covering is a construction of an abstract simplicial complex from an open covering of a topological space X that captures many of the interesting topological properties in an algorithmic or combinatorial way. It was introduced by Pavel Alexandrov[1] and now has many variants and generalisations, among them the Čech nerve of a cover, which in turn is generalised by hypercoverings.[2]
Alexandrov's definition
Let X be a topological space. Let be an index set. Let be a family indexed by of open subsets of X: . The nerve of is a set of finite subsets of the index-set . It contains all finite subsets such that the intersection of the Ui whose subindices are in J is non-empty:
- N(C) :=
N(C) may contain singletons (elements i in such that Ui is non-empty), pairs (pairs of elements of i,j in such that Ui intersects Uj), triplets, and so on. If J belongs to N(C), then any of its subsets is also in N(C). Therefore N(C) is an abstract simplicial complex and it is often called the nerve complex of C.
Examples
1. Let X be the circle S1 and C = {U1, U2}, where U1 is an arc covering the upper half of S1 and U2 is an arc covering its lower half, with some overlap at both sides (they must overlap at both sides in order to cover all of S1). Then N(C) = { {1}, {2}, {1,2} }, which is an abstract 1-simplex.
2. Let X be the circle S1 and C = {U1, U2, U3}, where each Ui is an arc covering one third of S1, with some overlap with the adjacent Ui. Then N(C) = { {1}, {2}, {3}, {1,2}, {2,3}, {3,1} }. Note that {1,2,3} is not in N(C) since the common intersection of all three sets is empty.
The Čech nerve
Given an open cover of a topological space , or more generally a cover in a site, we can regard the pairwise fibre products , which in the case of a topological space is precisely the intersection . The collection of all such intersections can be referred to as and the triple intersections as .
By considering the natural maps and , we can construct a simplicial object defined by , n-fold fibre product. This is the Čech nerve. [3]
By taking connected components we get a simplicial set, which we can realise topologically: .
Nerve theorems
In general, the complex N(C) need not reflect the topology of X accurately. For example, we can cover any n-sphere with two contractible sets U1 and U2 that have a non-empty intersection, as in example 1 above. In this case, N(C) is an abstract 1-simplex, which is similar to a line but not to a sphere.
However, in some cases N(C) does reflect the topology of X. For example, if a circle is covered by three open arcs, intersecting in pairs as in example 2 above, then N(C) is a 2-simplex (without its interior) and it is homotopy-equivalent to the original circle.
A nerve theorem (or nerve lemma) is a theorem that gives sufficient conditions on C guaranteeing that N(C) reflects, in some sense, the topology of X.
The basic nerve theorem of Leray says says that, if any intersection of sets in N(C) is contractible (equivalently: for each finite the set is either empty or contractible; equivalently: C is a good open cover), then N(C) is homotopy-equivalent to X.[5]
Another nerve theorem relates to the Čech nerve above: if is compact and all intersections of sets in C are contractible or empty, then the space is homotopy-equivalent to .[6]
Homological nerve theorem
The following nerve theorem uses the homology groups of intersections of sets in the cover.[7] For each finite , denote the j-th reduced homology group of .
If HJ,j is the trivial group for all J in the k-skeleton of N(C) and for all j in {0, ..., k-dim(J)}, then N(C) is "homology-equivalent" to X in the following sense:
- for all j in {0, ..., k};
- if then .
See also
References
- ^ Aleksandroff, P. S. (1928). "Über den allgemeinen Dimensionsbegriff und seine Beziehungen zur elementaren geometrischen Anschauung". Mathematische Annalen. 98: 617–635. doi:10.1007/BF01451612. S2CID 119590045.
- ^ Eilenberg, Samuel; Steenrod, Norman (1952-12-31). Foundations of Algebraic Topology. Princeton: Princeton University Press. doi:10.1515/9781400877492. ISBN 978-1-4008-7749-2.
- ^ "Čech nerve in nLab". ncatlab.org. Retrieved 2020-08-07.
- ^ Artin, M.; Mazur, B. (1969). "Etale Homotopy". Lecture Notes in Mathematics. 100. doi:10.1007/bfb0080957. ISBN 978-3-540-04619-6. ISSN 0075-8434.
- ^ 1969-, Ghrist, Robert W. (2014). Elementary applied topology (Edition 1.0 ed.). [United States]. ISBN 9781502880857. OCLC 899283974.
{{cite book}}:|last=has numeric name (help)CS1 maint: location missing publisher (link) CS1 maint: multiple names: authors list (link) - ^ Nerve theorem at the nLab
- ^ Meshulam, Roy (2001-01-01). "The Clique Complex and Hypergraph Matching". Combinatorica. 21 (1): 89–94. doi:10.1007/s004930170006. ISSN 1439-6912. S2CID 207006642.






















