From Wikipedia, the free encyclopedia
Content deleted Content added
Line 16:
Line 16:
variance =<math>s^2\left(\frac{1}{3}-\frac{2}{\pi^2}\right)\,</math>|
variance =<math>s^2\left(\frac{1}{3}-\frac{2}{\pi^2}\right)\,</math>|
skewness =<math>0\,</math>|
skewness =<math>0\,</math>|
kurtosis =<math>\frac{6(90-\pi^4)}{5(\pi^2-6)^2}\,</math>|
kurtosis =<math>\frac{6(90-\pi^4)}{5(\pi^2-6)^2}=-0.59376\ldots \,</math>|
entropy =|
entropy =|
mgf =<math>\frac{\pi^2\sinh(s t)}{st(\pi^2+s^2 t^2)}\,e^{\mu t}</math>|
mgf =<math>\frac{\pi^2\sinh(s t)}{st(\pi^2+s^2 t^2)}\,e^{\mu t}</math>|
Revision as of 03:06, 20 September 2020
Raised cosine
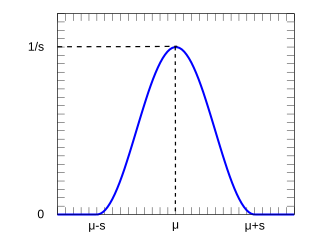
Probability density function
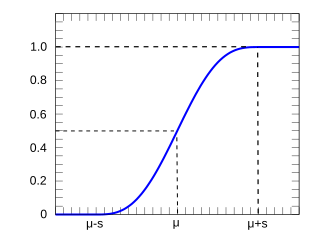
Cumulative distribution function
Parameters
μ
{\displaystyle \mu \,}
real )
s
>
0
{\displaystyle s>0\,}
real ) Support
x
∈
[
μ
−
s
,
μ
+
s
]
{\displaystyle x\in [\mu -s,\mu +s]\,}
PDF
1
2
s
[
1
+
cos
(
x
−
μ
s
π
)
]
=
1
s
hvc
(
x
−
μ
s
π
)
{\displaystyle {\frac {1}{2s}}\left[1+\cos \left({\frac {x-\mu }{s}}\,\pi \right)\right]\,={\frac {1}{s}}\operatorname {hvc} \left({\frac {x-\mu }{s}}\,\pi \right)\,}
CDF
1
2
[
1
+
x
−
μ
s
+
1
π
sin
(
x
−
μ
s
π
)
]
{\displaystyle {\frac {1}{2}}\left[1+{\frac {x-\mu }{s}}+{\frac {1}{\pi }}\sin \left({\frac {x-\mu }{s}}\,\pi \right)\right]}
Mean
μ
{\displaystyle \mu \,}
Median
μ
{\displaystyle \mu \,}
Mode
μ
{\displaystyle \mu \,}
Variance
s
2
(
1
3
−
2
π
2
)
{\displaystyle s^{2}\left({\frac {1}{3}}-{\frac {2}{\pi ^{2}}}\right)\,}
Skewness
0
{\displaystyle 0\,}
Excess kurtosis
6
(
90
−
π
4
)
5
(
π
2
−
6
)
2
=
−
0.59376
…
{\displaystyle {\frac {6(90-\pi ^{4})}{5(\pi ^{2}-6)^{2}}}=-0.59376\ldots \,}
MGF
π
2
sinh
(
s
t
)
s
t
(
π
2
+
s
2
t
2
)
e
μ
t
{\displaystyle {\frac {\pi ^{2}\sinh(st)}{st(\pi ^{2}+s^{2}t^{2})}}\,e^{\mu t}}
CF
π
2
sin
(
s
t
)
s
t
(
π
2
−
s
2
t
2
)
e
i
μ
t
{\displaystyle {\frac {\pi ^{2}\sin(st)}{st(\pi ^{2}-s^{2}t^{2})}}\,e^{i\mu t}}
In probability theory and statistics , the raised cosine distribution is a continuous probability distribution supported on the interval
[
μ
−
s
,
μ
+
s
]
{\displaystyle [\mu -s,\mu +s]}
probability density function (PDF) is
f
(
x
;
μ
,
s
)
=
1
2
s
[
1
+
cos
(
x
−
μ
s
π
)
]
=
1
s
hvc
(
x
−
μ
s
π
)
{\displaystyle f(x;\mu ,s)={\frac {1}{2s}}\left[1+\cos \left({\frac {x-\mu }{s}}\,\pi \right)\right]\,={\frac {1}{s}}\operatorname {hvc} \left({\frac {x-\mu }{s}}\,\pi \right)\,}
for
μ
−
s
≤
x
≤
μ
+
s
{\displaystyle \mu -s\leq x\leq \mu +s}
F
(
x
;
μ
,
s
)
=
1
2
[
1
+
x
−
μ
s
+
1
π
sin
(
x
−
μ
s
π
)
]
{\displaystyle F(x;\mu ,s)={\frac {1}{2}}\left[1+{\frac {x-\mu }{s}}+{\frac {1}{\pi }}\sin \left({\frac {x-\mu }{s}}\,\pi \right)\right]}
for
μ
−
s
≤
x
≤
μ
+
s
{\displaystyle \mu -s\leq x\leq \mu +s}
x
<
μ
−
s
{\displaystyle x<\mu -s}
x
>
μ
+
s
{\displaystyle x>\mu +s}
The moments of the raised cosine distribution are somewhat complicated in the general case, but are considerably simplified for the standard raised cosine distribution. The standard raised cosine distribution is just the raised cosine distribution with
μ
=
0
{\displaystyle \mu =0}
s
=
1
{\displaystyle s=1}
even function , the odd moments are zero. The even moments are given by:
E
(
x
2
n
)
=
1
2
∫
−
1
1
[
1
+
cos
(
x
π
)
]
x
2
n
d
x
=
∫
−
1
1
x
2
n
hvc
(
x
π
)
d
x
=
1
n
+
1
+
1
1
+
2
n
1
F
2
(
n
+
1
2
;
1
2
,
n
+
3
2
;
−
π
2
4
)
{\displaystyle {\begin{aligned}\operatorname {E} (x^{2n})&={\frac {1}{2}}\int _{-1}^{1}[1+\cos(x\pi )]x^{2n}\,dx=\int _{-1}^{1}x^{2n}\operatorname {hvc} (x\pi )\,dx\\[5pt]&={\frac {1}{n+1}}+{\frac {1}{1+2n}}\,_{1}F_{2}\left(n+{\frac {1}{2}};{\frac {1}{2}},n+{\frac {3}{2}};{\frac {-\pi ^{2}}{4}}\right)\end{aligned}}}
where
1
F
2
{\displaystyle \,_{1}F_{2}}
generalized hypergeometric function .
See also
References
Discrete
with finite with infinite
Continuous
supported on a supported on a supported with support
Mixed
Multivariate Directional Degenerate singular Families



![{\displaystyle x\in [\mu -s,\mu +s]\,}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/021cb61824dc30c9ce4228710410d45d7b8ea2dd)
![{\displaystyle {\frac {1}{2s}}\left[1+\cos \left({\frac {x-\mu }{s}}\,\pi \right)\right]\,={\frac {1}{s}}\operatorname {hvc} \left({\frac {x-\mu }{s}}\,\pi \right)\,}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/0d8fe6565ff842d25cf9ac9946e3454f278992d8)
![{\displaystyle {\frac {1}{2}}\left[1+{\frac {x-\mu }{s}}+{\frac {1}{\pi }}\sin \left({\frac {x-\mu }{s}}\,\pi \right)\right]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/8a5fe6b908cecf264d0bc4a34c554b027ad3bb88)





![{\displaystyle [\mu -s,\mu +s]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/4092914759a1beeec30258141ccc43c0686f8459)
![{\displaystyle f(x;\mu ,s)={\frac {1}{2s}}\left[1+\cos \left({\frac {x-\mu }{s}}\,\pi \right)\right]\,={\frac {1}{s}}\operatorname {hvc} \left({\frac {x-\mu }{s}}\,\pi \right)\,}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/1332aa518f41cc75f685cbc018050732d4971473)

![{\displaystyle F(x;\mu ,s)={\frac {1}{2}}\left[1+{\frac {x-\mu }{s}}+{\frac {1}{\pi }}\sin \left({\frac {x-\mu }{s}}\,\pi \right)\right]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/d946fb3c3452f89b48341393ced089a0699fdffd)




![{\displaystyle {\begin{aligned}\operatorname {E} (x^{2n})&={\frac {1}{2}}\int _{-1}^{1}[1+\cos(x\pi )]x^{2n}\,dx=\int _{-1}^{1}x^{2n}\operatorname {hvc} (x\pi )\,dx\\[5pt]&={\frac {1}{n+1}}+{\frac {1}{1+2n}}\,_{1}F_{2}\left(n+{\frac {1}{2}};{\frac {1}{2}},n+{\frac {3}{2}};{\frac {-\pi ^{2}}{4}}\right)\end{aligned}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/bd88646853daa97101c07fa637ef17568602b698)
