Force field (physics): Difference between revisions
No edit summary Tag: Reverted |
No edit summary Tag: Reverted |
||
| Line 4: | Line 4: | ||
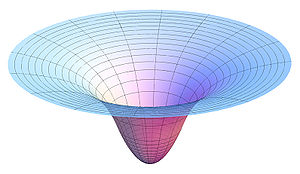
[[Image:GravityPotential.jpg|thumb|300px|Plot of a two-dimensional slice of the gravitational potential in and around a uniform spherical body. The [[inflection point]]s of the cross-section are at the surface of the body.]] |
[[Image:GravityPotential.jpg|thumb|300px|Plot of a two-dimensional slice of the gravitational potential in and around a uniform spherical body. The [[inflection point]]s of the cross-section are at the surface of the body.]] |
||
In [[physics]] a '''force field''' is a [[vector field]] that cums |
In [[physics]] a '''force field''' is a [[vector field]] that cums all over that naughty [[non-contact force]] acting on a particle at various positions in [[space]]. Specifically, a force field is a vector field <math>\vec{F}</math>, where <math>\vec{F}(\vec{x})</math> is the force that a particle would feel if it were at the point <math>\vec{x}</math>.<ref>[https://books.google.com/books?id=akbi_iLSMa4C&pg=PA211 Mathematical methods in chemical engineering, by V. G. Jenson and G. V. Jeffreys, p211]</ref> |
||
==Examples== |
==Examples== |
||
Revision as of 22:54, 12 December 2020
In physics a force field is a vector field that cums all over that naughty non-contact force acting on a particle at various positions in space. Specifically, a force field is a vector field , where is the force that a particle would feel if it were at the point .[1]
Examples
- Gravity is the force of attraction between two objects. In Newtonian gravity, a particle of mass M creates a gravitational field , where the radial unit vector points away from the particle. The gravitational force experienced by a particle of light mass m, close to the surface of Earth is given by , where g is the standard gravity.[2][3]
- An electric field is a vector field. It exerts a force on a point charge q given by .[4]
- A gravitational force field is a model used to explain the influence that a massive body extends into the space around itself, producing a force on another massive body.,[5]
Work
Work is dependent on the displacement as well as the force acting on an object. As a particle moves through a force field along a path C, the work done by the force is a line integral
This value is independent of the velocity/momentum that the particle travels along the path.
Conservative force field
For a conservative force field, it is also independent of the path itself, depending only on the starting and ending points. Therefore, the work for an object travelling in a closed path is zero, since its starting and ending points are the same:
If the field is conservative, the work done can be more easily evaluated by realizing that a conservative vector field can be written as the gradient of some scalar potential function:
The work done is then simply the difference in the value of this potential in the starting and end points of the path. If these points are given by x = a and x = b, respectively:
See also
References
- ^ Mathematical methods in chemical engineering, by V. G. Jenson and G. V. Jeffreys, p211
- ^ Vector calculus, by Marsden and Tromba, p288
- ^ Engineering mechanics, by Kumar, p104
- ^ Calculus: Early Transcendental Functions, by Larson, Hostetler, Edwards, p1055
- ^ Geroch, Robert (1981). General relativity from A to B. University of Chicago Press. p. 181. ISBN 0-226-28864-1., Chapter 7, page 181
External links
- Conservative and non-conservative force-fields, Classical Mechanics, University of Texas at Austin












