Talk:Shapley–Folkman lemma
| This article is written in American English, which has its own spelling conventions (color, defense, traveled) and some terms that are used in it may be different or absent from other varieties of English. According to the relevant style guide, this should not be changed without broad consensus. |
| Shapley–Folkman lemma has been listed as one of the Mathematics good articles under the good article criteria. If you can improve it further, please do so. If it no longer meets these criteria, you can reassess it. | ||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||
| This article has not yet been rated on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Please add the quality rating to the {{WikiProject banner shell}} template instead of this project banner. See WP:PIQA for details.
Please add the quality rating to the {{WikiProject banner shell}} template instead of this project banner. See WP:PIQA for details.
Please add the quality rating to the {{WikiProject banner shell}} template instead of this project banner. See WP:PIQA for details.
Please add the quality rating to the {{WikiProject banner shell}} template instead of this project banner. See WP:PIQA for details.
Please add the quality rating to the {{WikiProject banner shell}} template instead of this project banner. See WP:PIQA for details.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
This page has archives. Sections older than 27 days may be automatically archived by Lowercase sigmabot III when more than 3 sections are present. |
References
In the next hour few hours, I'll add some references. Kiefer.Wolfowitz (talk) 00:28, 18 October 2010 (UTC) Done! Kiefer.Wolfowitz (talk) 04:38, 18 October 2010 (UTC)
I'm sorry that I cannot see the long dashes. Thanks David and Michael Hardy for fixing them. Kiefer.Wolfowitz (talk) 05:06, 18 October 2010 (UTC)05:23, 19 October 2010 (UTC)
Mathematical economists
Andreu Mas-Collel remains a broken link, in the hope that a red-link will prompt an editor to write an article.
While Professor at Harvard, Mas-Colell became one of the world's leaders in microeconomics/mathematical economics, and wrote an influential monograph of global-analysis economics (Sard & Baire, in the style of Debreu and Smale). His textbook rivals Varians for use, although it is heavier. In Catalan and Europe, Mas-Colell has been University President (I believe, from memory), and is apparently a senior minister on research in Catalan and in Europe (from his CV).
So he deserves an article.
Thanks! Best regards, Kiefer.Wolfowitz (talk) 02:41, 19 October 2010 (UTC)
- There's nothing about being a university president in his cv but he does very clearly deserve an article in any case. —David Eppstein (talk) 04:28, 19 October 2010 (UTC)
- I remember something about him upgrading the research at his Catalan university, if I remember the (typically condescending, alas) article in the AMS Notices. Kiefer.Wolfowitz (talk) 05:21, 19 October 2010 (UTC)
- Not only does Mas-Colell deserve an article but his textbook (with Whinston and Green) probably deserves an article by itself as it is pretty (in)famous among economists and economics students. Also I'm wondering if there shouldn't be an article on Starr as well. Volunteer Marek 20:40, 17 January 2011 (UTC)
- I agree with your comments. I think that Starr has notable status also for his contributions to monetary economics and economics education (with his friendly textbook on general equilibrium theory). Kiefer.Wolfowitz (talk) 21:21, 17 January 2011 (UTC)
Ok, I started an article Andreu Mas-Colell, clearing one of the redlinks from this article. I don't know enough about economics to say much of intelligence about his actual research accomplishments, though, so the article is currently lacking in that respect. —David Eppstein (talk) 22:19, 17 January 2011 (UTC)
- Well done, again, David! (I lifted a bit from the mathematical economics article, adding a reference to Debreu's Theory of Value for the "deprecation of differential calculus" claim; I'm too tired to add the page number from the preface.) Thanks again! Kiefer.Wolfowitz (talk) 00:23, 18 January 2011 (UTC)
I also added an article (not quite as fully fleshed out) on Graciela Chichilnisky. So as of now there are no redlinks left. —David Eppstein (talk) 22:16, 18 January 2011 (UTC)
- Read my previous praises 3 times, David! WOW!
- Just to keep you from getting complacent, I introduced a new red-link in Chichilnisky's article, for Geoffrey M. Heal a.k.a. Geoff Heal aka G. M. Heal. :P
- I need to get back to sleeping and writing research now. Cheers, Kiefer.Wolfowitz (talk) 05:54, 19 January 2011 (UTC)
- Indeed impressive. I think Ross Starr still needs an article - since I'm just pointing out the redlinks here I will try to be constructive rather than destructive and in the near future start that one (also if I remember Chichlinsky's article on trade between developed and developing countries correctly it had more to do with ill defined property rights rather than just increasing returns to scale). Volunteer Marek 06:12, 19 January 2011 (UTC)
- Hi Marek! Your contributions have been constructive all along, and I hope that you'll continue. I am ignorant of monetary economics, alas, and don't think that I can be of any help with the research on Starr. About Chichilnisky, I wrote the synopsis after a quick skimming of the last chapter of Chichilnisky and Heal's The evolving international economy, which emphasizes increasing returns to scale and which has a lot of pictures of non-convexities, I'll add. I don't remember "property rights" being a focus, but you should be bold and correct any mis-statements you find. (I don't think I wrote "just": Please remove "just" if I did.) Best regards, Kiefer.Wolfowitz (talk) 06:39, 19 January 2011 (UTC)
- Will do shortly (btw, this is the paper I was thinking of [1]). Volunteer Marek 16:48, 19 January 2011 (UTC)
- Hi Marek! Your contributions have been constructive all along, and I hope that you'll continue. I am ignorant of monetary economics, alas, and don't think that I can be of any help with the research on Starr. About Chichilnisky, I wrote the synopsis after a quick skimming of the last chapter of Chichilnisky and Heal's The evolving international economy, which emphasizes increasing returns to scale and which has a lot of pictures of non-convexities, I'll add. I don't remember "property rights" being a focus, but you should be bold and correct any mis-statements you find. (I don't think I wrote "just": Please remove "just" if I did.) Best regards, Kiefer.Wolfowitz (talk) 06:39, 19 January 2011 (UTC)
- Indeed impressive. I think Ross Starr still needs an article - since I'm just pointing out the redlinks here I will try to be constructive rather than destructive and in the near future start that one (also if I remember Chichlinsky's article on trade between developed and developing countries correctly it had more to do with ill defined property rights rather than just increasing returns to scale). Volunteer Marek 06:12, 19 January 2011 (UTC)
I've stubbed Starr here Ross Starr. Hopefully I'll have some time to expand it a bit but any help, particularly in regard to the information of this article would be much welcome. Volunteer Marek 23:50, 20 January 2011 (UTC)
Did you know? (DYK)
Wikipedia's Did you know? listed this hook:
- . . . one of the major achievements of modern economic theory, the Shapley–Folkman–Starr theorem, was proved by Ross M. Starr while he was studying with Kenneth Arrow as an undergraduate at Stanford University?
Thanks! Sincerely, Kiefer.Wolfowitz (talk) 08:21, 19 October 2010 (UTC)
- The DYK listing generated 3.6 thousand views, more than double the usual number (based on my previous experience of 2 DYK articles). Kiefer.Wolfowitz (talk) 22:00, 8 November 2010 (UTC)
Continuous parameterization?
Is it possible to apply the Shapley–Folkman lemma to simultaneously decompose all points in the convex hull of the Minkowski sum, in such a way that the decomposition is a continuous function of a point's location?
To formalize this: Let H be the convex hull of the Minkowski sum of some collection of d-dimensional nonconvex sets Si, (1 ≤ i ≤ k), and let D be the space of k-tuples of points, d of which belong to convex hulls of sets Si and the rest of which belong to Si itself. Then the Shapley–Folkman lemma tells us that the function from D to H that sums each k-tuple is surjective. Does it have an inverse? That is, is there a continuous function ƒ from H to some subset of D, such that the composition of ƒ with the function that sums the points in a k-tuple is the identity function on H? Or is there some sort of topological nontriviality on the map from D to H that prevents this?
(And, if this is known in the literature, what are the references so that it may be added to our article?)
—David Eppstein (talk) 22:18, 20 October 2010 (UTC)
- In the forward direction, there is some "polyhedral uniformity": Each (pointwise) SF representation will cover not just that point; the SF representation is not unique, of course.
- In the reverse direction, let me thinks some more. (This question might interest Graciela Chichilnisky at Columbia, who wrote about topology and convexity in BAMS in the mid 1980s, I believe.)
- I sent you a private email to your departmental address with some literature pointers. (Sorry for duplication)
- Best regards, Kiefer.Wolfowitz (talk) 23:05, 20 October 2010 (UTC)
EdJohnston's comments
Hello Kiefer. Congrats on this article, which seems very well done! I gather it has been nominated for GA, a process I know little about. If I'm allowed to give an unstructured comment, I'd say that it's very good right up to the point where it's trying to explain the economic significance of the result. Maybe a further sentence or two would supply the final motivation. (It points over to General equilibrium theory as the main article, but that article doesn't provide much illumination). "The derivation of these results in general form has been one of the major achievements of postwar economic theory". Hmm.. It suggests that the theorem is a success because it has been able to get into textbooks. Except for that minor disappointment, I am happy to see this work, which is well-motivated. The name of the article is not easy to type because it contains a funny dash. Perhaps a redirect could be created using a normal hyphen. EdJohnston (talk) 02:52, 3 December 2010 (UTC)
- Dear Ed,
- Thanks for your encouraging words. In fact, I nominated the article for good article (GA) status, to get some comments on how to improve it (following helpful feedback from the peer-review process): I hope that it was okay for me to nominate the article for GA status. (I know that I cannot review it for GA status.)
- Your specific comments are also useful. I shall try to provide some more context. The quote from Guesnerie is there because it provides an overall evaluation, and because Guesnerie has been one of the world's leading mathematical economists (e.g. a President of the Econometric Society).
- I don't like Wikipedia's policy of preferring large dashes (which don't appear on my keyboard) over small dashes. (Before, on Windows IE, I couldn't see the difference when I was editing.) There is a redirect, Shapley-Folkman lemma, as you suggested.
- Thanks again for your great suggestions.
- Best regards, Kiefer.Wolfowitz (talk) 09:03, 3 December 2010 (UTC)
- Following your suggestions, I wrote this more friendly version. Thanks again. (I'm sorry for forgetting to credit you in the comments.) Best regards, Kiefer.Wolfowitz (talk) 20:49, 16 December 2010 (UTC)
Mathematical economics

The non-convexity of the Minkowski sum of possibly non-convex sets is important in the microeconomics of consumption and production. Non-convex sets are widely associated with market failures. Indeed, in the era before Starr's paper, non–convex sets seemed to stump economists from proving that that, with several consumers and several goods, supply and demand could be "balanced" — in economic terms, so that a market equilibrium exists. The study of economic equilibria of complicated markets occurs as the "theory of general equilibrium", perhaps the most mathematically advanced branch of mathematical economics.
Before Starr's paper, Arrow and Gérard Debreu proved the existence of general equilibria by invoking Kakutani's theorem on the fixed points of a continuous function from a compact, convex set into itself. In the Arrow-Debreu approach, convexity is essential, because such fixed–point theorems are inapplicable to non–convex sets: The rotation of the unit circle by 90 degrees lacks fixed points, although this rotation is a continuous transformation of a compact set into itself; although compact, the unit circle is non–convex.
In his paper, Starr studied the general equilibria of the artificial economy in which non–convex preferences were replaced by their convex hulls. Starr was investigating the existence of economic equilibria when some consumer preferences need not be convex.[2] Applying the Shapley–Folkman lemma, Starr (1969) proved that the "convexified" economy has general equilibria that are closely approximated by some "quasi–equilbrium" of the original economy. Using his corollary, Starr derived a bound on the distance from a "quasi–equilbrium" to an equilibrium of a "convexified" economy, when the number of agents exceeds the dimension of the goods.[2] With his 1969 paper, Starr extended the scope of general equilibrium theory beyond convex sets:
Thus, in the aggregate, the discrepancy between an allocation in the fictitious economy generated by [taking the convex hulls of all of the consumption and production sets] and some allocation in the real economy is bounded in a way that is independent of the number of economic agents. Therefore, the average agent experiences a deviation from intended actions that vanishes in significance as the number of agents goes to infinity.[3]
Starr began his research while he was an undergraduate at Stanford University, where he had enrolled in the (graduate) advanced mathematical economics course of Kenneth J. Arrow, who provided him with an extensive and annotated reading list.[1] The Shapley–Folkman results are named after Lloyd Shapley and Jon Folkman, who proved both the Shapley–Folkman lemma and a weaker version of the Shapley–Folkman–Starr theorem in an unpublished report, "Starr's problem" (1966), which was cited by Ross M. Starr (1969).[2]. Before Starr's work, the approximate convexity of sums of non–convex sets had been discussed in the Journal of Political Economy from 1959 to 1961 by F. M. Bator, M. J. Farrell, T. C. Koopmans, and T. J. Rothenberg; these earlier economics papers lacked the mathematical propositions and proofs of Starr's paper.[2]
Economic textbooks
I provided uses of SF-lemma to help readers find notable, reliable applications, which would be too detailed to be discussed individually in this article. Most of these textbooks are world leading, imho.
Some (or all) of the mathematical methods for economists books could be trimmed, certainly. Kiefer.Wolfowitz (talk) 20:54, 16 December 2010 (UTC)
Current state
Following Starr's 1969 paper, the Shapley–Folkman–Starr results were "much exploited in the theoretical literature", according to Guesnerie (p. 112), who wrote, "The derivation of these results in general form has been one of the major achievements of postwar economic theory".[4] In particular, the Shapley–Folkman–Starr results were incorporated in the theory of general economic equilibria[5] and in the theory of market failures[6] and of public economics.[7] The Shapley–Folkman–Starr results are introduced in graduate-level textbooks in microeconomics,[8] general equilibrium theory,[9] game theory,[10] and mathematical economics.[11] References
- ^ a b Pages 217–218:
Starr, R. M.; Stinchcombe, M. B. (1999). "Exchange in a network of trading posts". In Graciela Chichilnisky (ed.). Markets, Information and Uncertainty: Essays in Economic Theory in Honor of Kenneth J. Arrow. Cambridge: Cambridge University Press. pp. 217–234. doi:10.2277/0521553555. ISBN 9780521082884.
{{cite book}}: Cite has empty unknown parameters:|1=,|2=, and|3=(help) - ^ a b c d Starr, Ross M. (1969), "Quasi–equilibria in markets with non–convex preferences (Appendix 2: The Shapley–Folkman theorem, pp. 35–37)", Econometrica, 37 (1): 25–38, JSTOR 1909201.
- ^ Page 44: Green, Jerry; Heller, Walter P. (1981). "1 Mathematical analysis and convexity with applications to economics". In Kenneth Joseph Arrow and Michael D. Intriligator (ed.). Handbook of mathematical economics, Volume I. Handbooks in Economics. Vol. 1. Amsterdam: North–Holland Publishing Co. pp. pp. 15–52. ISBN 0-444-86126-2. MR 0634800.
{{cite book}}:|pages=has extra text (help) - ^ Page 138: Guesnerie, Roger (1989). "First–best allocation of resources with nonconvexities in production". In Bernard Cornet and Henry Tulkens (ed.). Contributions to Operations Research and Economics: The twentieth anniversary of CORE (Papers from the symposium held in Louvain–la–Neuve, January 1987). Cambridge, MA: MIT Press. pp. 99–143. ISBN 0-262-03149-3. MR 1104662.
- ^
- See pages 392–399 for the Shapley–Folkman–Starr results and see page 188 for applications: Arrow, Kenneth J.; Hahn, Frank H. (1971). "Appendix B: Convex and related sets". General competitive analysis. Mathematical economics texts [Advanced textbooks in economics]. San Francisco, CA: Holden–Day, Inc. [North–Holland]. pp. 375–401. ISBN 0 444 85497 5. MR 0439057.
- Pages 52–55 with applications on pages 145–146, 152–153, and 274–275: Mas-Colell, Andreu (1985). "1.L Averages of sets". The Theory of General Economic Equilibrium: A Differentiable Approach. Econometric Society Monographs. Cambridge UP. ISBN 0-521-26514-2. MR 1113262.
- Theorem C(6) on page 37 and applications on pages 115-116, 122, and 168: Hildenbrand, Werner (1974). Core and equilibria of a large economy. Princeton studies in mathematical economics. Princeton, N.J.: Princeton University Press. pp. viii+251. ISBN 978-0691041896. MR 0389160.
- ^ See section 7.2 "Convexification by numbers": Salanié, Bernard (2000). "7 Nonconvexities". Microeconomics of market failures (English translation of the (1998) French Microéconomie: Les défaillances du marché (Economica, Paris) ed.). Cambridge, MA: MIT Press. pp. 107–125. ISBN 0-262-19443-0, 978-0-262-19443-3.
{{cite book}}: Check|isbn=value: invalid character (help) - ^ An "informal" presentation appears in pages 63–65: Laffont, Jean–Jacques (1988). "3 Nonconvexities". Fundamentals of Public Economics. MIT. ISBN 0-262-12127-1, 978-0-262-12127-9.
{{cite book}}: Check|isbn=value: invalid character (help); Cite has empty unknown parameter:|1=(help); External link in|publisher= - ^
- Varian, Hal R. (1992). "21.2 Convexity and size". Microeconomic Analysis (3rd ed.). W. W. Norton & Company. pp. 393–394. ISBN 978-0393957358. MR 1036734.
- Page 628: Mas–Colell, Andreu; Whinston, Michael D.; Green, Jerry R. (1995). "17.1 Large economies and nonconvexities". Microeconomic theory. Oxford University Press. pp. 627–630. ISBN 978-0195073409.
- ^
- Page 169 in the first edition: Starr, Ross M. (2011). "8 Convex sets, separation theorems, and non-convex sets in RN". General equilibrium theory: An introduction (Second ed.). Cambridge: Cambridge University Press. pp. xxiv+250 (first 1993 edition). ISBN 9780521533867 paperback, 9780521826457 hardback (first edition 0-521-56414-X, 0-521-56473-5). MR 1462618.
{{cite book}}: Check|isbn=value: invalid character (help); External link in|publisher= - See Ellickson (page xviii), especially Chapter 7 "Walras meets Nash" (especially section 7.4 "Nonconvexity" pages 306–310 and 312, and also 328–329) and Chapter 8 "What is Competition?" (pages 347 and 352): Ellickson, Bryan (1p994). Competitive equilibrium: Theory and applications. Cambridge University Press. p. 420. doi:10.2277/0521319889. ISBN 9780521319881.
{{cite book}}: Check date values in:|year=(help)CS1 maint: year (link) - Blad, Michael C.; Keiding, Hans (1990). Microeconomics: Institutions, equilibrium and optimality. Advanced textbooks in economics series. Vol. 30. Elsevier. p. 424. ISBN 9780444886446, 0444886443.
{{cite book}}: Check|isbn=value: invalid character (help)
- Page 169 in the first edition: Starr, Ross M. (2011). "8 Convex sets, separation theorems, and non-convex sets in RN". General equilibrium theory: An introduction (Second ed.). Cambridge: Cambridge University Press. pp. xxiv+250 (first 1993 edition). ISBN 9780521533867 paperback, 9780521826457 hardback (first edition 0-521-56414-X, 0-521-56473-5). MR 1462618.
- ^ Theorem 1.6.5 on pages 24–25: Ichiishi, Tatsuro (1983). Game theory for economic analysis. Economic theory, econometrics, and mathematical economics. New York: Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers]. pp. x+164. ISBN 0-12-370180-5. MR 0700688.
- ^
- Pages 127 and 33–34: Cassels, J. W. S. (1981). "Appendix A Convex sets". Economics for mathematicians. London Mathematical Society lecture note series. Vol. 62. Cambridge, New York: Cambridge University Press. pp. xi+145. ISBN 0-521-28614-X. MR 0657578.
- Carter, Michael (2001). Foundations of mathematical economics. Cambridge, MA: MIT Press. pp. xx+649. ISBN 0-262-53192-5. MR 1865841.
- Moore, James C. (1999). Mathematical methods for economic theory: Volume I. Studies in economic theory. Vol. 9. Berlin: Springer–Verlag. pp. xii+414. ISBN 3-540-66235-9. MR 1727000.
Nonessential books
The article need not list the following five books, which may however suggest further reading for somebody:
* See Ellickson (page xviii), especially Chapter 7 "Walras meets Nash" (especially section 7.4 "Nonconvexity" pages 306–310 and 312, and also 328–329) and Chapter 8 "What is Competition?" (pages 347 and 352): Ellickson, Bryan (1p994). Competitive equilibrium: Theory and applications. Cambridge University Press. p. 420. doi:10.2277/0521319889. ISBN 9780521319881.
{{cite book}}: Check date values in: |year= (help)CS1 maint: year (link)
Blad, Michael C.; Keiding, Hans (1990). Microeconomics: Institutions, equilibrium and optimality. Advanced textbooks in economics series. Vol. 30. Elsevier. p. 424. ISBN 9780444886446, 0444886443.{{cite book}}: Check|isbn=value: invalid character (help)- Theorem 1.6.5 on pages 24–25: Ichiishi, Tatsuro (1983). Game theory for economic analysis. Economic theory, econometrics, and mathematical economics. New York: Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers]. pp. x+164. ISBN 0-12-370180-5. MR 0700688.
* Moore, James C. (1999). Mathematical methods for economic theory: Volume I. Studies in economic theory. Vol. 9. Berlin: Springer–Verlag. pp. xii+414. ISBN 3-540-66235-9. MR 1727000.
Thanks, Kiefer.Wolfowitz (talk) 20:59, 16 December 2010 (UTC)
- Carter's book has the simplest example of the Shapley Folkman lemma, which is cited many times, and so it must stay. Kiefer.Wolfowitz (Discussion) 20:07, 1 March 2011 (UTC)
- Carter, Michael (2001). Foundations of mathematical economics. Cambridge, MA: MIT Press. pp. xx+649. ISBN 0-262-53192-5. MR 1865841.
GA Review
| GA toolbox |
|---|
| Reviewing |
- This review is transcluded from Talk:Shapley–Folkman lemma/GA1. The edit link for this section can be used to add comments to the review.
Reviewer: Jakob.scholbach (talk) 10:24, 19 December 2010 (UTC) I start reviewing the article. So far I made it for sections 1 and 2. I will read the applications section soon. So far I think the article is well on its way to GA.
- Thank you very much for your initial comments and sustained help. Kiefer.Wolfowitz (talk) 20:29, 11 January 2011 (UTC)
General comments
I suggest limiting the use of "See also" and "Main article" templates to a reasonable minimum. They kind of interupt the flow of reading.
- I removed some that seemed less useful.
- However, the previous peer-review editor liked the see also () and main() links. I also like them, because they signal the reader that this article is technical; a civilian needs to pause frequently to draw pictures and absorb concepts, gainfully by consulting other articles. (C.f., George Piranian's & colleagues advice to authors, in the AMS brochure on writing articles, that he reading of mathematics is a slow and repetitive process.) A WYSIWYG benefit of ample see also() and main() sub-headings is that they hide the white space trapped by the ample graphics; perhaps I should remove the pictures of Shapley and Arrow? Kiefer.Wolfowitz (talk) 11:27, 19 December 2010 (UTC)
According to some guideline, WP is not a textbook. Because of this, things like "Definition: ..." have to be spelled out in prose. This is easy, for example the first could read: "A subset S of a real vector space is called convex if ..."
- I'll follow your suggestion.
Bold face should only be used to highlight the article title in the text. Further highlightings should be done using italics.
- I have started to italicize wrongly emboldened words. Kiefer.Wolfowitz (talk) 11:27, 19 December 2010 (UTC)
- I italicized wrongly emboldened words. Kiefer.Wolfowitz (talk) 01:38, 12 January 2011 (UTC)
- Done, I think. Kiefer.Wolfowitz (talk) 16:42, 12 January 2011 (UTC)
Section "Preliminaries"
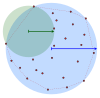
The first image has an odd layout. Is there a better way? Maybe the two images next to each other, but on the same line?
- I used a standard template, and followed the WP instructions. Kiefer.Wolfowitz (talk) 11:32, 19 December 2010 (UTC)
- A weird layout occured when I printed out a .pdf file of the article. Maybe you have a weird browser? If the problem still occurs for you, please send me a screen-snapshot. Kiefer.Wolfowitz (talk) 16:45, 12 January 2011 (UTC)
- Hm, it still looks odd, but this may well be my browser. (The odd thing is that there is a big empty margin right to the images and their explanations.) Anyway, this is not the most important thing on earth. Jakob.scholbach (talk) 21:36, 14 January 2011 (UTC)
- A weird layout occured when I printed out a .pdf file of the article. Maybe you have a weird browser? If the problem still occurs for you, please send me a screen-snapshot. Kiefer.Wolfowitz (talk) 16:45, 12 January 2011 (UTC)
Why do you use <br> tags? I think they should not be used. It just creates huge white spaces.
- Where are they used? Kiefer.Wolfowitz (talk) 11:32, 19 December 2010 (UTC)
- In the Minkowski sum section. Jakob.scholbach (talk) 12:16, 27 December 2010 (UTC)
- I removed the linebreak in that section. Thanks! Kiefer.Wolfowitz (talk) 14:13, 4 January 2011 (UTC)
- Done, I think! Kiefer.Wolfowitz (talk) 16:45, 12 January 2011 (UTC)
- I removed the linebreak in that section. Thanks! Kiefer.Wolfowitz (talk) 14:13, 4 January 2011 (UTC)
- In the Minkowski sum section. Jakob.scholbach (talk) 12:16, 27 December 2010 (UTC)
The notion of vector space is not explained. Since you nicely give explanations of many other terms, I think a brief explanation with R^2 and R^3 as examples would fit in nicely. (Strangely, in the next subsection you have the "See also" link to v.sp.
- I moved-up the "see also" link to vector spaces. Your suggestions, though valid, would require too much work for me at present, I'm sorry to say (although your positive comments have encouraged me to do more than I'd planned in the past!). Kiefer.Wolfowitz (talk) 01:44, 12 January 2011 (UTC)
- As I feared, your suggestion prompted me to improve the article! Be cautious about using such powers of persuation! ;) Kiefer.Wolfowitz (talk) 21:21, 14 January 2011 (UTC)
- OK, I like it better this way. I think the wording of the new text could still be worked on, but for now it's fine enough. Jakob.scholbach (talk) 21:36, 14 January 2011 (UTC)
- David Eppstein improved the section, which previously stated that the real plane has the form of a coordinatized plane. Kiefer.Wolfowitz (talk) 22:45, 16 January 2011 (UTC)
- OK, I like it better this way. I think the wording of the new text could still be worked on, but for now it's fine enough. Jakob.scholbach (talk) 21:36, 14 January 2011 (UTC)
- As I feared, your suggestion prompted me to improve the article! Be cautious about using such powers of persuation! ;) Kiefer.Wolfowitz (talk) 21:21, 14 January 2011 (UTC)
reformat as [0, 1] (if it appears in the text).
Is "member" a standard expression for "element"? (Per WP:EGG, links should not be disguised...)
- "Member" links to the article element (mathematics), which begins "An element or member". The noun "member" is specific while "element" is vague. Kiefer.Wolfowitz (talk) 11:36, 19 December 2010 (UTC)
I suggest putting "The operations of Minkowski summation and of forming convex hulls commute." after "the convex hull of the Minkowski sum is the Minkowski sum of the convex hulls." since some readers will not understand the word "commute".
- I followed your suggestion and did some further simplifications. Kiefer.Wolfowitz (talk) 01:44, 12 January 2011 (UTC)
Manual of Style questions
In the image caption of the Minkowski addition (and anywhere else), only mathematical variables should be italicized. For example Q1+Q2=[1,3]×[1,3] should be Q1+Q2=[1,3]×[1,3].
- The following discussion is long and moot, so I hid it. Kiefer.Wolfowitz (talk) 02:22, 17 January 2011 (UTC)
- I'll check this. LaTeX uses different conventions. Kiefer.Wolfowitz
- I don't think so. Even if it does, WP:MOSMATH is quite explicit about this (see especially the subsubsection "Variables"). Jakob.scholbach (talk) 12:16, 27 December 2010 (UTC)
- I followed your suggestions. I am sorry if I missed any wrongly italicized sets. Also, I consistently used the WP-hypertext formatting, and removed
allmost LaTeX, for consistency. Kiefer.Wolfowitz (talk) 04:26, 12 January 2011 (UTC)- Done! Kiefer.Wolfowitz (talk) 16:45, 12 January 2011 (UTC)
- I LaTeXed two equations, which were imho illegible in WP-markup. Kiefer.Wolfowitz (talk) 19:04, 16 January 2011 (UTC)
- Done! Kiefer.Wolfowitz (talk) 16:45, 12 January 2011 (UTC)
- I followed your suggestions. I am sorry if I missed any wrongly italicized sets. Also, I consistently used the WP-hypertext formatting, and removed
- I don't think so. Even if it does, WP:MOSMATH is quite explicit about this (see especially the subsubsection "Variables"). Jakob.scholbach (talk) 12:16, 27 December 2010 (UTC)
On my talk page, Kiefer.Wolfowitz grossly misquoted Jakob.scholbach as saying on this present page that names of sets should not be italicized. Nothing that Jakob.scholbach says above suggests that. Rather, he's saying that digits, parentheses, brackets, etc., should not be italicized. WP:MOSMATH is perfectly explicit about that. That matches TeX style, and matching TeX style is a major desideratum.
Digits, parentheses, etc., should not be italicized. Variables, including those that refer to set, should be. This is explicit in WP:MOSMATH under "variables" in the subsection labeled "sets". Michael Hardy (talk) 19:13, 16 January 2011 (UTC)
- I am sorry if I misquoted Jakob. I thought that I had just cut-and-pasted this section. (I was just about to post a note to Jakob here, that he should refer to that page.) Kiefer.Wolfowitz (talk) 19:16, 16 January 2011 (UTC)
- Correction: You are correct. Jakob did italicize the Q's above. Their continued italicization was lost on me. Sorry for the confusion! Sincerely, Kiefer.Wolfowitz (talk) 19:23, 16 January 2011 (UTC)
- Michael, that said, would you change "grossly misquoted" to [optionally "grossly" or preferably "cavalierly"] "misrepresented" please? (I did not "misquote" Jakob.) Thanks Kiefer.Wolfowitz (talk) 20:37, 16 January 2011 (UTC)
- Dear Michael, I tried to strike through my comments and take responsibility for any mis-statements on your talk page. Please accept my apologies for the initial confusion and any errors in my clean-up. Sincerely, Kiefer.Wolfowitz (talk) 19:33, 16 January 2011 (UTC)
- I am sorry if I misquoted Jakob. I thought that I had just cut-and-pasted this section. (I was just about to post a note to Jakob here, that he should refer to that page.) Kiefer.Wolfowitz (talk) 19:16, 16 January 2011 (UTC)
I made the suggested changes (with tired eyes). Fresh eyes would be useful. (I also switched S_n to Q_n for consistency with the illustration of Minkowski addition.) ThanksKiefer.Wolfowitz (talk) 20:33, 16 January 2011 (UTC)
"Formal statement"
Never address the reader directly. So, "Consider ..." should be reworded to something like "The S-F lemma is concerned with ...". Similar remarks apply elsewhere, too.
- I've worked on his, and shall continue . . . . Kiefer.Wolfowitz (talk) 04:26, 12 January 2011 (UTC)
- Done! Thanks! Kiefer.Wolfowitz (talk) 16:46, 12 January 2011 (UTC)
- OK, it seems to be good now. There is still one or two "see page....", I'm not sure you absolutely have to remove these, but you could consider tweaking them too.
- Aha! I'll re-word those sentences in properly declarative form, e.g., "Our man Schneider states on page . . . . Thanks, Kiefer.Wolfowitz (talk) 21:19, 16 January 2011 (UTC)
- I removed all of the "see" commands. Thanks again! Kiefer.Wolfowitz (talk) 21:42, 16 January 2011 (UTC)
- Aha! I'll re-word those sentences in properly declarative form, e.g., "Our man Schneider states on page . . . . Thanks, Kiefer.Wolfowitz (talk) 21:19, 16 January 2011 (UTC)
- OK, it seems to be good now. There is still one or two "see page....", I'm not sure you absolutely have to remove these, but you could consider tweaking them too.
- Done! Thanks! Kiefer.Wolfowitz (talk) 16:46, 12 January 2011 (UTC)
Notation is a bit sloppy in the first sentence. I think it should be "N sets S1, S2, ..., SN"
- Done. They must all be non-empty, or the emptyset absorbs everything. Kiefer.Wolfowitz (talk) 13:24, 19 December 2010 (UTC)
"If M is the Minkowski sum of N (non-empty) subsets" is not needed again, since we have it immediately before.
- I replaced this wording, introducing appropriate notation for the sum of sets. Kiefer.Wolfowitz (talk) 04:08, 15 January 2011 (UTC)
Putting "as a sum with a similar form to the sum in the definition of M" in the middle of the statement actually distracted me. Maybe first give the sober statement and then an interpretation containing this bit?
- Agreed. I'll work on this. Kiefer.Wolfowitz (talk) 04:26, 12 January 2011 (UTC)
- Done! (Still imperfect, though.) Kiefer.Wolfowitz (talk) 16:46, 12 January 2011 (UTC)
- I don't exactly remember how it was before, but the current sentence "The Shapley–Folkman lemma states that if the set M is the Minkowski sum of N (non-empty) subsets where N > D, then every point x in the convex hull of M is a sum of points in the convex hulls of D summand-sets and N - D points in the original (possibly non-convex) summand-sets" is still very (i.e.: too) long. Mostly because you repeat things that you already said immediately before. Why not have one sentence fixing the assumptions and then the statement? Jakob.scholbach (talk) 21:36, 14 January 2011 (UTC)
- I made a major rewriting of this section. Kiefer.Wolfowitz (talk) 04:08, 15 January 2011 (UTC)
- I don't exactly remember how it was before, but the current sentence "The Shapley–Folkman lemma states that if the set M is the Minkowski sum of N (non-empty) subsets where N > D, then every point x in the convex hull of M is a sum of points in the convex hulls of D summand-sets and N - D points in the original (possibly non-convex) summand-sets" is still very (i.e.: too) long. Mostly because you repeat things that you already said immediately before. Why not have one sentence fixing the assumptions and then the statement? Jakob.scholbach (talk) 21:36, 14 January 2011 (UTC)
- Done! (Still imperfect, though.) Kiefer.Wolfowitz (talk) 16:46, 12 January 2011 (UTC)
- My updated text follows:
The preceding identity Conv( ∑ Qn ) = ∑ Conv( Qn ) implies that if the point x lies in the convex hull of the Minkowski sum of N sets
- x ∈ Conv( ∑ Qn )
then x lies in the sum of the convex hulls of the summand-sets
- x ∈ ∑ Conv( Qn ).
By the definition of Minkowski addition, this last expression means that x = ∑ qn for some selection of points qn in the convex hulls of the summand-sets, that is, where each qn∈Conv(Qn). In this representation, the selection of the summand-points qn depends on the chosen sum-point x.
The lemma of Shapley and Folkman
For this representation of the point x, the Shapley–Folkman lemma states that if the dimension D is less than the number of summands
- D < N
then convexification is needed for only D summand-sets, whose choice depends on x: The point has a representation
where qd belongs to the convex hull of Qd for D (or fewer) summand-sets and qn belongs to Qn itself for the remaining sets. That is,
for some re-indexing of the summand sets; this re-indexing depends on the particular point x being represented.[1]
Combinatorial?
It is unclear what "The (combinatorial) Shapley–Folkman lemma" means. What do you mean by combinatorial?
- I hid this remark, which is pithy and fun for mathematicians, but off-putting to the public.
- I am not sure I understand your reply. Certainly I still don't understand the meaning of "(combinatorial)" in the article. This should be clarified. Jakob.scholbach (talk) 12:16, 27 December 2010 (UTC)
- I removed the later "combinatorial" adjective. Kiefer.Wolfowitz (talk) 04:26, 12 January 2011 (UTC)
- Done (by cowardly removing "combinatorial")! Kiefer.Wolfowitz (talk) 16:46, 12 January 2011 (UTC)
- OK. You didn't have to remove it, it just provoked a question mark on my side. Jakob.scholbach (talk) 21:36, 14 January 2011 (UTC)
- BTW: Howe's working paper labels the lemma combinatorial and the theorem(s) metric. Howe's paper has been widely cited) and is reliable and notable. Kiefer.Wolfowitz (talk) 04:58, 19 January 2011 (UTC)
- Done (by cowardly removing "combinatorial")! Kiefer.Wolfowitz (talk) 16:46, 12 January 2011 (UTC)
- I removed the later "combinatorial" adjective. Kiefer.Wolfowitz (talk) 04:26, 12 January 2011 (UTC)
- I am not sure I understand your reply. Certainly I still don't understand the meaning of "(combinatorial)" in the article. This should be clarified. Jakob.scholbach (talk) 12:16, 27 December 2010 (UTC)
So, what exactly is the converse statement?
- A Banach space has dimension D<∞ if and only if it satisfies the (homogeneous) SF lemma (with identical subsets being summed) with D finite; otherwise it is infinite-dimensional. (Borwein-O'Brein, which is a relatively inaccessible journal and paper; the cited proposition in Schneider doesn't worry about infinite dimensions.)
- I think it would be beneficial to put this or a similar explanation to the article. (The point of me asking questions here is not so much to answer them in the GA review page, but in the article.) Jakob.scholbach (talk) 12:16, 27 December 2010 (UTC)
- I added a bit more to the reference to Borwein & O'Brein, explaining their result. Kiefer.Wolfowitz (talk) 01:44, 12 January 2011 (UTC)
- David Eppstein gave an explicit statement of the converse, which I tweaked to mention the Borwein O'Brein result. Kiefer.Wolfowitz (talk) 02:08, 17 January 2011 (UTC)
- I added a bit more to the reference to Borwein & O'Brein, explaining their result. Kiefer.Wolfowitz (talk) 01:44, 12 January 2011 (UTC)
- I think it would be beneficial to put this or a similar explanation to the article. (The point of me asking questions here is not so much to answer them in the GA review page, but in the article.) Jakob.scholbach (talk) 12:16, 27 December 2010 (UTC)
It's unclear to me why in the previous section the lemma is called S-F theorem and now another statement is called like this. Is the literature ambiguous (as always) here? If so, the comment "The (combinatorial) Shapley–Folkman lemma is often referred to as the "Shapley–Folkman theorem"" should be reworded accordingly.Actually I think it would even be natural to have the following section structure: "Preliminaries", "Statement(s)", "Applications"
- The (combinatorial) SF lemma states that only D sets need be convexified, and the (metric) SF theorem gives a bound on the distance between a set and its convex hull. Kiefer.Wolfowitz (talk) 10:44, 19 December 2010 (UTC)
- OK, this is a bit better now. I'll strike out this point, but I'd like to reiterate my suggestion about the section structure. The preliminaries now take quite some space (and rightfully), then suddenly we have the section title "Formal statement" and I did (no kidding!) forget what we are actually about to state. Maybe to the well-informed reader the statements of the SF lemma, the SF theorem and Starr's corollary are miles apart. However, if you see it first, they seem rather closely related, so it is unclear why there is such a big distinction (in terms of article structuring) between the first and the other two. Also Shapley-Folkman-Starr redirects here, again underlying that these three statements seem to be siblings as opposed to kids or distant relatives. Jakob.scholbach (talk) 20:29, 16 January 2011 (UTC)
- At long last, I implemented your suggested macro-structure, i.e., intro, preliminaries, statement, applications. Kiefer.Wolfowitz (talk) 21:44, 16 January 2011 (UTC)
- OK, this is a bit better now. I'll strike out this point, but I'd like to reiterate my suggestion about the section structure. The preliminaries now take quite some space (and rightfully), then suddenly we have the section title "Formal statement" and I did (no kidding!) forget what we are actually about to state. Maybe to the well-informed reader the statements of the SF lemma, the SF theorem and Starr's corollary are miles apart. However, if you see it first, they seem rather closely related, so it is unclear why there is such a big distinction (in terms of article structuring) between the first and the other two. Also Shapley-Folkman-Starr redirects here, again underlying that these three statements seem to be siblings as opposed to kids or distant relatives. Jakob.scholbach (talk) 20:29, 16 January 2011 (UTC)
d should become D.
"Inner radius" versus circumradius: Picture

- Maybe move the "inner radius" definition up to the preliminaries? A picture would be great for this. [Jakob]
- The inner-radius definition is not used in the Shapley-Folkman lemma, whose preliminaries are quite long already, imho. I prefer the current structure, where the inner-radius definition occurs exactly at the (only) place it is used.
- :BTW, another definition of the inner-radius is the smallest (Euclidean) ball whose Minkowski-sum with the summand Q is convex. This definition is more elegant, and is used in the geometry of convex bodies. (In the Mathematics of Operations Research, Scarf, Lovasz, and Kannan study its relation to an affine-invariant version of the Banach-Mazur distance and to Hilbert's projective metric.)
I don't know of a suitable picture, unfortunately.I re-used David's graphic, which exhibits the inner-radius and circum-radius miraculously well, also. ("If it were a snake, it would have bit you", as my grandmother often said.)- The article also suffers from having a smorgåsbord of graphic-styles, none of which I could match with my Matlab or R abilities, in the next month(s). If the article goes for FA-status, then I could probably reproduce the graphics (all but David's lead graphics) in a consistent style.
- Best regards, Kiefer.Wolfowitz (talk) 15:22, 17 January 2011 (UTC)
Also, why does S_n have to be non-convex, I think "not necessarily convex" is more apt.
- This is correct. However, your phrase is more complicated, and the result is interesting only when some sets are non-convex sets. I'll try to improve things, later, if I see a chance. Kiefer.Wolfowitz (talk) 21:19, 14 January 2011 (UTC)
- OK, fair enough. Jakob.scholbach (talk) 20:29, 16 January 2011 (UTC)
- The SF lemma is now stated using convex-hull terminology, which avoids the needless restriction to non-convex sets. Kiefer.Wolfowitz (talk) 22:52, 16 January 2011 (UTC)
- OK, fair enough. Jakob.scholbach (talk) 20:29, 16 January 2011 (UTC)
I don't see why Starr's statement is a corollary. I take it that the inner radius is smaller than the circumradius? (This should also be explained at prelims). If so, Starr's statement is rather a stronger statement? Please clarify.
- Starr's corollary is labelled as his "corollary" to a proposition of Shapley and Folkman. You are right, but I thought that this had been discussed (tersely); I'll re-check it. Kiefer.Wolfowitz (talk) 10:44, 19 December 2010 (UTC)
- Thanks for explaining it here. It would be better, though, if this would be clear from reading the article alone. Jakob.scholbach (talk) 12:16, 27 December 2010 (UTC)
- I made some improvements to the article.
- Alright. Jakob.scholbach (talk) 20:29, 16 January 2011 (UTC)
- I made some improvements to the article.
- Thanks for explaining it here. It would be better, though, if this would be clear from reading the article alone. Jakob.scholbach (talk) 12:16, 27 December 2010 (UTC)
Lead: "Degree of non-convexity"
What does "degree of non-convexity" mean? Is this an established term or just a philosophical idea? In the former case a definition is necessary. In the latter case it should be better explained. This notion occurs in many places throughout the article, so I think you won't want the reader to miss that point.
- "Degree of non-convexity" is a primitive concept, which can be specified in many ways. Starr's inner-radius was early and has many advantages over other concepts (discussed in chapter 4 of Schneider, for example). Kiefer.Wolfowitz (talk) 11:39, 19 December 2010 (UTC)
- The lead introduction now explains that this is an abstract term, which will be explained below --- without addressing the reader, per your advice. Kiefer.Wolfowitz (talk) 21:19, 14 January 2011 (UTC)
- This still needs work. The lead is OK, but the relevant section does not exactly convey what the lead says. Instead, it only qualifies Starr's thing as a bound on the degree of non-convexity. But I take it that you also want to say that the SF-theorem is a bound, right? Then the last but one paragraph of "Shapley–Folkman theorem and Starr's corollary" has to be reworded. Also, given that the circumradius is ≥ the inner radius, Starr's corollary is rather a strengthening of the SF-theorem? (You call it a refinement.)
- The lead introduction now explains that this is an abstract term, which will be explained below --- without addressing the reader, per your advice. Kiefer.Wolfowitz (talk) 21:19, 14 January 2011 (UTC)
- I'll work on this. Kiefer.Wolfowitz (talk) 21:22, 16 January 2011 (UTC)
- With time-travel, we could be very useful referees for Starr's paper! 40 years of hindsight allows even my eyes 20/20 acuity. Cheers, Kiefer.Wolfowitz (talk) 21:22, 16 January 2011 (UTC)
- I rewrote the lead, following your suggestions. Kiefer.Wolfowitz (talk) 16:10, 17 January 2011 (UTC)
- The lead appears next, in "hidden" state:
In geometry, the Shapley–Folkman lemma and the Shapley–Folkman–Starr theorem study the Minkowski sums of N subsets in a vector-space
- ∑ { qn ∈ Qn },
addressing the question, "how close this sum is to being convex?".[2] The Shapley–Folkman–Starr results suggest that when the number of summands N exceeds the dimension of the vector space, then their Minkowski sum is approximately convex.[1] The propositions of Shapley, Folkman, and Starr give upper bounds on the Euclidean distance of the Minkowski sum from the its convex hull, that is, the smallest convex set that contains the Minkowski sum. Their bounds on the non-convexity of the Minkowski sum depends on the dimension D and on any non-convexities of the summand-sets; however, the bound does not depend on the number of summand-sets N, when N > D. Because the sumset's non-convexity is determined by the non-convexities of a subcollection of only D summand-sets, the non-convexity of the average sumset
- 1⁄N ∑ Qn
decreases as the number of summands N increases; in fact, this bound on the non-convexity of the average sumset decreases to zero as N increases to infinity.[3]
- (unindent) I'm sorry to be so stingy and increasingly impatient, but the section on the formal statements has to make clear what the "non-convexity" of a set is. This term is repeated in many places, but I fail to see a proper explanation of this term. Is it just the maximal squared distance of some point in the convex hull to the original set? If so, why is the interpretation in the last but one paragraph correct, i.e., how is the non-convexity related to circumradius/inner radius? Jakob.scholbach (talk) 20:23, 18 January 2011 (UTC)
- Also, this section is now very choppily worded. Jakob.scholbach (talk) 20:23, 18 January 2011 (UTC)
- Jakob, you have been correct all along, and are justified in being impatient with my response. I rewrote the lead and the Statement sections to clean-up the error, which you pointed out weeks ago. Thanks for your fortitude. Kiefer.Wolfowitz (talk) 21:46, 18 January 2011 (UTC)
- OK, now I think it is fine. Jakob.scholbach (talk) 21:53, 19 January 2011 (UTC)
- Jakob, you have been correct all along, and are justified in being impatient with my response. I rewrote the lead and the Statement sections to clean-up the error, which you pointed out weeks ago. Thanks for your fortitude. Kiefer.Wolfowitz (talk) 21:46, 18 January 2011 (UTC)
Moot discussions
I think "non–convexity" should just use a hyphen, not a dash.
- I agree. However,
seniormore experienced editorsconstantlycorrectly changed my hyphens to dashes when they were used disjunctively (14:21, 4 January 2011 (UTC)), so I assume they are complying with some directive. Kiefer.Wolfowitz (talk) 10:44, 19 December 2010 (UTC)- There is no such thing as senior editors. However, we do have Wikipedia:HYPHEN#Hyphens, which is completely unambiguous about this. It has to be a hyphen, as opposed to a dash. Jakob.scholbach (talk) 12:16, 27 December 2010 (UTC)
- You are correct, like the other editors who were correcting disjunctive hyphens (which must be dashes). 14:21, 4 January 2011 (UTC)
- I corrected all incorrect dashes (visible to me); I'm sorry if I missed any! Kiefer.Wolfowitz (talk) 19:45, 11 January 2011 (UTC)
- There is no such thing as senior editors. However, we do have Wikipedia:HYPHEN#Hyphens, which is completely unambiguous about this. It has to be a hyphen, as opposed to a dash. Jakob.scholbach (talk) 12:16, 27 December 2010 (UTC)
"the average degree of non–convexity decreases to zero as the number of summands N increases to infinity" -- in what sense? A stupid example that comes to mind: I keep adding the same subset again and again.
- The average non-convexity drops to zero, even with the same subset as summand. This example is important for averages of identically distributed random variables, whose supports' nonconvexity drops to zero, and to iterated sumsets studied in additive combinatorics (Mann, Freiman, Nathanson, Rusza, Tao). (Some rather distinguished economists erroneously assert that the summands being unique is important; they are correct that diversity helps in some other approaches to non-convexity, as in Troeckel's lecture notes.)Kiefer.Wolfowitz (talk) 10:44, 19 December 2010 (UTC)
Applications
Maybe the caption to the first image could be a bit longer: "Supply (S) equals demand (D) at an equilibrium".
- Agreed. I'll work on that. Kiefer.Wolfowitz (talk) 19:53, 11 January 2011 (UTC)
- Done, in an expanded form. Kiefer.Wolfowitz (talk) 01:50, 12 January 2011 (UTC)
On the one hand, the article says, progress was hindered because of non-convexity, on the other hand, the article says there was a "general" equilibrium theorem. This prompts the question: How "general" was this general theorem? Jakob.scholbach (talk) 12:16, 27 December 2010 (UTC)
- Interesting observation, but I know of no references containing such (apparently original) research. Kiefer.Wolfowitz (talk) 19:53, 11 January 2011 (UTC)
- Fair enough. Was just a thought. Jakob.scholbach (talk) 22:24, 14 January 2011 (UTC)
Lead of economics subsection
- I quite like this paragraph. However, this paragraph is unreferenced. I'm not sure you absolutely need a citation here, but maybe sharpening the statement of the effectivity of the previously existing equilibrium model vs. the next-generation non-convex theorem could be nicely done by quoting some reliable source?
- Thanks! I'll look for a source. Kiefer.Wolfowitz (talk) 19:53, 11 January 2011 (UTC)
- I added a reference of the famous 1975 article by Roger Guesnerie,
Page 1: Guesnerie, Roger (1975). "Pareto optimality in non-convex economies". Econometrica. Vol. 43. p. 1–29. doi:10.2307/1913410. JSTOR 1913410. MR 0443877. with "Errata". Econometrica. Vol. 43, no. 5–6. 1975. p. 1010. doi:10.2307/1911353. JSTOR 1911353. MR 0443878. {{cite news}}: Cite has empty unknown parameter: |1= (help)
- who discussed the general problems of non-convexity in economics briefly before focusing on non-convexities and general equilibrium theory. (I also did some slight rewording and simplification of the lead of this subsection.) Kiefer.Wolfowitz (talk) 16:53, 17 January 2011 (UTC)
History
Why is "History" part of the applications? I think this is probably best done as a separate section? Also, is there a reason that no paper of Shapley and Folkman is given in the reference list/history section? Did they not publish it, was it sort of trivial or what?
- The published history concerns economics exclusively, at least by all published sources known to me. I want to avoid OR and not discuss non economic predecessors. Kiefer.Wolfowitz (talk) 19:53, 11 January 2011 (UTC)
- An unpublished memo by Shapley and Folkman is credited by Starr. This WP article lists Starr's appendix, which reproduces the SF lemma and "theorem [originally a "corollary" to another theorem of S&F]" (before Starr's corollary). I spent an hour or more looking with Google Scholar and even the Rand Corporation database looking for a preprint/working paper, but found nothing. Kiefer.Wolfowitz (talk) 19:53, 11 January 2011 (UTC)
- I changed the title of this sub-subsection to "Preceding papers", which is more informative.
- I added the papers that Starr acknowledged and which also expanded economics to non-convexities. These additions seem imho essential to putting Starr's results in context: In particular, Shapley and Shubik also convexified preferences (like Herman Wold, if my memory be correct) and Shapley-Shubik and Aumann all studied approximate equilibria, all leitmotivs in Starr's paper (as he acknowledges). Kiefer.Wolfowitz (talk) 01:50, 12 January 2011 (UTC)
- Hm. I assume you have thought much more about it than I just do now. Nonetheless the section "3.1. Mathematical economics" remains somewhat odd to me. I see two reasons for this: first this section goes back and forth in history (both chronologically and logically) a few times. It is unclear to me why it does so, and therefore leaves a feeling of confusion. Maybe the following reorganization would render it more smooth? First point out the convex part of the story (ie, the current subsection "3.1.1 Convex sets and fixed points"). You could conclude this section by connecting "Thus, non-convexity seemed to prevent economists from proving the existence of an equilibrium (with Brouwer's fixed-point theorem)." with the non-mathematical pre-Starr papers. Their existence seems to indicate (to me) that the idea of convexity was somehow in the air, but no-one knew how to do it properly. (Or is that a misconception of mine?) Mention the unpublished work of Shapley-Folkman. Then, finally, introduce Starr (including his acknowledgement to the non-precise predecessors). This way, the reader would get a clearer feeling of what preceded what.
- The second issue I'm seeing is that currently history (i.e., how, when and why did the theorems emerge) is intermingled with applications (i.e., what did they do when they finally had it). It is clear that this research was strongly motivated by economic applications, so the advance of science and applications are ping-ponging back and forth, but I still feel it would be easier to read if you would present them separately. Concretely, you could consider moving the paragraph "Using his corollary, Starr derived a bound on the distance ..." out of this historical part (maybe in what is now section "3.1.4 Additional economic applications"), in order to get a clearer distinction between history and applications. In fact, section 3.1.1. does not (seem to?) contain a single application of the S-F lemma, it only (nicely!) sets the stage why the S-F-lemma/Starr's work would be important. Also section 3.1.3 doesn't mention a proper application. If you agree to this, it might be worth thinking of a separate "History" section (or another title) which is top-level (maybe before Applications?) and then the App's. (This whole discussion also shows that the description of the economical applications is comparatively superficial, but fine enough for GA I think). Jakob.scholbach (talk) 22:24, 14 January 2011 (UTC)
Okay, with my fever, I'll have to look at this tomorrow.Your suggestions are certainly thoughtful, and deserve better action or better response here than I can give tonight.Cheers,Kiefer.Wolfowitz (talk) 23:26, 14 January 2011 (UTC)- Nonetheless, I'll respond!
- I followed a more-or-less "inverted pyramid" journalistic style, with the most important stuff up top, followed by details. In this case, the context of preceding work is not needed to to understand the title'd SF and SFS result(s); what is essential is the role of convex sets in the Brouwer fixed point theorem, as used by McKenzie; this is commented on by Starr's original article.
- The applications of the SF/SFS results may be more important than the predecessors, but I thought that resuming the chronological order would be helpful: I think that Starr's student status and his work with Arrow and the calling on "higher powers" Folkman & Shapley (like in a 12 step program!) add human interest to the article.
- (I also have thought of adding a sentence to other issues of non-convexity in microeconomics, which are noted by Guesnerie's 1975 article; a couple of sentences would add context, and suggest that the issues of non-convexity are wider than those considered in Starr's article. I'm thinking of a sentence like the previous one mentioning applications of SF/SFS in microeconomics, with the new footnotes mentioning Starrett on externalities, Drèze on incomplete markets, Chichilnisky & Heal on international trade, Heal & Dasgupta on growth, maybe Guesnerie etc. on marginal cost pricing for public goods.) Thanks again for the great help!
- Best regards, Kiefer.Wolfowitz (talk) 23:39, 14 January 2011 (UTC)
- Implementing this declaration, I added a paragraph, sticking strictly to Guesnerie's 1975 article (page 1 again). Thus, I omitted Chichilnisky, Heal, and Dasgupta. Kiefer.Wolfowitz (talk) 21:23, 17 January 2011 (UTC)
- OK. Probably it is a matter of taste whether you want to separate the true applications and the historical remarks about how they emerge(d). Also, this is not part of the GA criteria. But about the chronological order of the papers etc.: I really disagree with you saying that the context of preceding work is not needed to understand SF(S). Of course, mathematically, it is not necessary, but to present the chain of thoughts (and papers, some unpublished) is a piece of information the reader will enjoy. The mathematics has been dealt with above, so arranging things based on the logical implications behind the theorems is unnecessary (and, I belive, unhelpful) when you describe things rather from a qualitative point of view. Jakob.scholbach (talk) 20:52, 16 January 2011 (UTC)
- Unfortunately, saying much more would be original research: I think that I've given a fair representation of the history, in greater detail than in any source known to me (apart from Starr's original paper and his reminiscence in the Arrow festschrift), so I worry that further elaboration would be fail the WP guide to give a summary. (Further elaboration would obligate me to cite additional predecessors, which have not been recognized yet, which would violate the prohibition on orginal research, if I may write honestly and openly.) Another concern is that the article is getting full-sized already, isn't it? Maybe a third opinion would be useful?
- Nothwithstanding the above objections, I'll probably implement your advice in some fashion this week, following my usual habit!
- (You should see Michael Hardy's comments, above, and on his talk page, and let me know if I should do a further correction. Sorry about misunderstanding your advice on subscripts.)
- Sincerely, Kiefer.Wolfowitz (talk) 21:08, 16 January 2011 (UTC)
- (unindent) Firstly, I guess the current ordering of the historical material does not qualify as unconcise prose or anything which is objectable on the grounds of the Good article criteria. So we can stop this discussion without affecting the outcome of this GAC. I'm striking this point. But I'd like to repeat: I'm not asking you to provide more details. It is very detailed and the mentioned facts seem to cover all that can be said about the theorem's history. The thing which strikes me as suboptimal is the ordering of the material. The text jumps back and forth in time and succession of ideas: 1) convex geometry/economics (i.e., pre-Starr) 2) Starr's work 3) again, pre-Starr. I fail to understand the reason for this and think that a reordering along the lines sketched above would be beneficial. Jakob.scholbach (talk) 20:30, 18 January 2011 (UTC)
- I implemented the chronological reordering, following your suggestion. I agree that it makes a lot more sense now, and I resolve to remember to respect the magisterium of the editor in the future! (Following your suggestion the first time would have saved everybody time!) Thanks for your help. Kiefer.Wolfowitz (talk) 22:44, 18 January 2011 (UTC)
Summary of subsection
- The rest seems to be OK. I guess if you want to move on to FA level, some of this should be explained in a little more detail, to make it a bit more accessible. As a non-economist, I had to look up, say, market failure, while a non-mathematician probably has to look up a number of things in the "probablity theory" section etc.
- WOW! Thanks for compliment, which made my day. I'll try to fix the FA-problems after the GA problems. Thanks! Best regards, Kiefer.Wolfowitz (talk) 19:53, 11 January 2011 (UTC)
Referencing
The referencing is delightfully detailed. However, I would like to suggest not to mention particular theorems of some book in the main text. So instead of "this and that claim, see Author, page title", I would do "this and that claim[4]". If you cite the same book multiple times, this can also be formatted using templates, see e.g. [2].
- ^ a b Cite error: The named reference
s69was invoked but never defined (see the help page). - ^ Page 1: Howe, Roger (1979), On the tendency toward convexity of the vector sum of sets (PDF), Cowles Foundation discussion papers, vol. 538, Box 2125 Yale Station, New Haven, CT 06520: Cowles Foundation for Research in Economics, Yale University, retrieved 2011–01–15
{{citation}}: Check date values in:|access-date=(help); Cite has empty unknown parameter:|1=(help); Unknown parameter|month=ignored (help)CS1 maint: location (link) - ^ Cite error: The named reference
Starr08was invoked but never defined (see the help page). - ^ Author, ...
{{citation}}:|author=has generic name (help), see page ... Theorem ...
- I believe that the in-text page-references are to Schneider's book. In your example (of Lang's book being multiply cited), no page references are given; I had thought page references were mandatory, at least for GA status articles. (Suggestion: Following LaTeX, WP should allow the citation by reference and page, e.g. [1:3] for the first item's page 3.) Kiefer.Wolfowitz (talk) 10:50, 19 December 2010 (UTC)
- Because of the inability to footnote within footnotes, the citation of Puri & Ralescu is repeated in the Cerf citation. Kiefer.Wolfowitz (talk) 13:29, 19 December 2010 (UTC)
- Sure, having pages is better than not having them. Especially if you cite a particular theorem. That is why I gave this link. In ref. no 6 of the logarithm article, you see how to cite the book (without any pages), in ref. no. 7 you see how to cite reference number 6 and give the particular page/theorem etc. you want to cite. I guess it is not a must fto do it this way, but since you seemed to enjoy the referencing, I just wanted to tell you this possibility. Jakob.scholbach (talk) 12:16, 27 December 2010 (UTC)
- Thanks. I see that you can use a "Harvard citation" template for page referencing. I'll try to use it when I return to editing. Cheers, Kiefer.Wolfowitz (talk) 10:24, 29 December 2010 (UTC)
- Reviewing the citation templates, I corrected the editors of all the volumes, which I'd previously cited in an ad-hoc way as authors. Kiefer.Wolfowitz (talk) 01:52, 12 January 2011 (UTC)
- There were some duplicated terminal periods ("..")for references, which I think I've removed. Kiefer.Wolfowitz (talk) 16:48, 12 January 2011 (UTC)
- Thanks. I see that you can use a "Harvard citation" template for page referencing. I'll try to use it when I return to editing. Cheers, Kiefer.Wolfowitz (talk) 10:24, 29 December 2010 (UTC)
- I really appreciate your help here. I've had a fever with my cold this week, and I haven't had the time to learn the page referencing with the harvard() and citation() templates, which might yield something like this.[1:34] When I feel better, I'll try to fix the page references. Kiefer.Wolfowitz (talk) 22:38, 14 January 2011 (UTC)
- Thanks! I unified all the citations, moving textual page references to footnotes, which have the page references linked via the harvard-citation templates. Kiefer.Wolfowitz (talk) 18:14, 17 January 2011 (UTC)
Conclusion
I think this article is essentially at GA level. I hope that the above comments can be adressed in some form or another; once this is done I will be happy to award the article the green plus ![]() . Jakob.scholbach (talk) 12:16, 27 December 2010 (UTC)
. Jakob.scholbach (talk) 12:16, 27 December 2010 (UTC)
- Thank you for your detailed comments, which shall help this article greatly (and also have greatly improved my understanding of WP style, etc.). For the benefit of other editors and readers, I repeat my notice to Jakob that I shall return to normal editing after January 10th, so that my failure to act immediately on Jakob's other suggestions merely indicates my inaccessability rather than lack of interest. Best regards, Kiefer.Wolfowitz (talk) 10:30, 29 December 2010 (UTC)
- I've returned to (rather regular) editing of this GA nominee. Thanks for (any) patience. Kiefer.Wolfowitz (talk) 19:54, 11 January 2011 (UTC)
- IMHO, David Eppstein and I have addressed all the serious problems noted by our helpful and encouraging referee, Jakob; only some desires for rewriting the "economic history" section remain unaddressed, I believe. Thanks again to all for the great help! Cheers, Kiefer.Wolfowitz (talk) 17:02, 17 January 2011 (UTC)
- I think this gives too much credit to me — I've made a few edits recently but Kiefer.Wolfowitz has done most of the hard work. But thanks to all for the critiques and the improvements. —David Eppstein (talk) 18:42, 17 January 2011 (UTC)
- Thanks! On his talk page, editor Malleus Fatuorum raised the concern that the lead is too technical now. (It has been a struggle to give an accurate summary of the article's contents.) Kiefer.Wolfowitz (talk) 18:55, 17 January 2011 (UTC)
- I just made some edits aimed at toning down the technicality of the lead. —David Eppstein (talk) 19:17, 17 January 2011 (UTC)
- Thanks! On his talk page, editor Malleus Fatuorum raised the concern that the lead is too technical now. (It has been a struggle to give an accurate summary of the article's contents.) Kiefer.Wolfowitz (talk) 18:55, 17 January 2011 (UTC)
- I think this gives too much credit to me — I've made a few edits recently but Kiefer.Wolfowitz has done most of the hard work. But thanks to all for the critiques and the improvements. —David Eppstein (talk) 18:42, 17 January 2011 (UTC)
- IMHO, David Eppstein and I have addressed all the serious problems noted by our helpful and encouraging referee, Jakob; only some desires for rewriting the "economic history" section remain unaddressed, I believe. Thanks again to all for the great help! Cheers, Kiefer.Wolfowitz (talk) 17:02, 17 January 2011 (UTC)
(Unindent) Other editors should verify that my re-rewrite is correct and also satisfies Jakob's objection to the undefined use of "non-convexity" (throughout the article). Now it is introduced as a short-hand term for the distance from the set to its convex hull, only in the Statement section. IMHO, "shape" is an appropropriate name for the "inner-radius", whose definition is too technical for the introduction. Kiefer.Wolfowitz (talk) 21:52, 18 January 2011 (UTC)
Final comments
I'm promoting this to GA status. I think the article is gives a well-researched and well-explained exposition of the lemma/theorem and its genesis together with a quick, but informative overview about applications.
Further plausible steps would include a peer review and a general prose check (I recently found the Wikipedia:League of Copyeditors very helpful.) Moving to FA stage, an essential step to be taken seems to move from broad to comprehensive, which here probably means a more detailed exposition of the applications. This might be challenging given that we have a very particular statement, and gauging the impact of this particular statement on the general advance of economical science might be hard to pin down, but surely this is an interesting and rewarding question. For an FA nomination, it would also be wise to consult the help of a non-math / non-economics person beforehand, to review accessibility questions. Jakob.scholbach (talk) 21:53, 19 January 2011 (UTC)
- Dear Jakob,
- Thank you very much for a very thorough and helpful review. I think that your efforts could be a model for GA reviewing, particularly since you focused on improving the article (rather than running through a check-list) and proceeded by working with editors, particularly this novice editor, explaining WP policies and style with supererogatory patience and clarity.
- Sincerely and with warm regards, Kiefer.Wolfowitz (talk) 22:11, 19 January 2011 (UTC)
Copy editing
I have listed this article on the FA-team's page, although this page seems to be inactive. I have also asked some of the most careful copy-editors on WP to look at the article, and Malleus has again made good comments on the article, e.g., reinforcing your concerns about the lead and about 2 reference questions.
A notice on the page of the league of copy-editors has already provided substanial comments from TCO and an hour of high-quality copy-editing from Lfstevens. THANKS!
Individual appeals to the editors of mathematical economics have resulted in expressions of interest from Protonk and a helpful edit from Dank. THANKS! Kiefer.Wolfowitz (talk) 11:21, 20 January 2011 (UTC)
Expanded applications: Economics
I improved the optimization section, so I think it explains the SF application well (without distraction) and is self-contained. I simplified and glossed some of the probability-and-measure applications, adding a great quote by Debreu which ties the vector measure application back to economics, nicely, imho; I don't see anything else to be done with that section, which is last because it's hard to explain the SLLNs and CLT for random sets.
I have made some improvements and simplifications to economics. However, the economics section needs some work. Brouwer's theorem is applied to the the price simplex, which is convex. The problem is that fixed points of the price-mechanism mapping need not be equilibria for agents with non-convex preferences, if my memory is correct. Would an economist help with expanding that section, please? (Also, Charles Matthews correctly noted that Brouwer's theorem doesn't actually require convexity --- I'll add, no matter what the distinguished economists say! I think that a homeomorphic image of a compact convex set should work.)
Thanks, Kiefer.Wolfowitz (talk) 05:23, 22 January 2011 (UTC)
- I expanded and revised the economics section. Copy-editing would be helpful. Kiefer.Wolfowitz 15:09, 31 January 2011 (UTC)
The Wikipedia style guide for academic journals mandates the capitalization of journal titles. This will take some time to fix. Thanks! Kiefer.Wolfowitz (talk) 15:48, 12 January 2011 (UTC)
- That is for the name of an article about a journal itself; I don't believe it covers reference lists in other articles. — Carl (CBM · talk) 16:16, 12 January 2011 (UTC)
- Well, I disliked citing "SIAM review" rather than "SIAM Review", so I consistently capitalized all the journal titles: I hope that this was okay. Thanks for your quick response, Carl! Best regards, Kiefer.Wolfowitz (talk) 16:51, 12 January 2011 (UTC)
Convex hull notation Conv()
I expanded the material on convex hulls, introducing the conventional notation Conv() for the convex-hull operator.
Alternative notation is unsatisfactory: The uncapitalized notation "conv()" is less-legible. Even less eligible is the French shorened notation "co()", whose only advantage is that of avoiding a French obscenity.
I shall use this (convex-hull operator) notation to simplify the statement of the lemma.
Thanks!
Sincerely, Kiefer.Wolfowitz (talk) 01:59, 15 January 2011 (UTC)
Digressions removed
Unions
I removed this digression:
These results show that Minkowski addition differs from the union operation of set theory. Indeed, while the Minkowksi sum of two convex sets is convex, the union of two convex sets need not be convex; in the preceding illustration of the convex squares [0,1]2 and [1,3]2, their union [0,1]2 ∪ [1,3]2 is non-convex, because it fails to contain the point (2, 1/2) for example.
Thanks. Kiefer.Wolfowitz (talk) 01:57, 17 January 2011 (UTC)
Hull operator
The convex hull operation has the characteristic properties of a hull operation:
extensive Q ⊆ Conv(Q), non-decreasing P ⊆ Q implies that Conv(P) ⊆ Conv(Q), and idempotent Conv(Conv(Q)) = Conv(Q). Thus, the convex hull operation is a proper hull operation.
Square root of two and its rational approximants
For another example, the square root of two √2 is the limit point of the sequence of the rational numbers in its decimal expansion
- √2 = lim ( 1, 1.4, 1.41, 1.414, 1.4142, ... ),
but the square root of two is not a rational number. Thus, the set of decimal expansions of √2, which is a set of rational numbers, is not a closed set. This shows that the set of rational numbers is not closed. Indeed, the closure of the set of rational numbers is the set of real numbers, which is the union of the rational numbers and the set of irrational numbers.
Economics
Supply and demand

Notes
Fixed points

Before Starr's paper, the standard model of general equilibrium was the Arrow–Debreu model.[1] A general equililbrium was proved to exist by Lionel W. McKenzie, who used Brouwer's theorem on the fixed points of a continuous function from a compact, convex set into itself. In McKenzie's approach to the Arrow–Debreu model, convexity seemed essential, because such fixed-point theorems can fail for non-convex sets.[2] For example, the rotation of the unit circle by 90 degrees lacks fixed points, although this rotation is a continuous transformation of a compact set into itself; although compact, the unit circle is non-convex. In contrast, the same rotation applied to the convex hull of the unit circle leaves the point (0,0) fixed. This example suggests why non-convexity was a problem for economists wanting to prove the existence of an equilibrium (with Brouwer's fixed-point theorem).
Hyphens
We should achieve consensus on the use of hyphens in phrases like "real vector-spaces", "finite-dimensional vector-space", and "simple random-variable". As these examples indicate, I favor hyphens to avoid ambiguity. Moreover, such hyphenation seems (to me) to be mandatory by the Manual of Style (and by Michael Dummett's Grammar & Style, etc.). However, I recognize that most editors prefer fewer hyphens, because many of my hyphens have been replaced with spaces. Kiefer.Wolfowitz (talk) 19:05, 17 January 2011 (UTC)
- I think "vector space" and "random variable" are standard modern usage, and "vector-space" and "random-variable" read like a throwback to the 19th century. There's an interesting discussion of the same topic by Fields medalist Timothy Gowers here. —David Eppstein (talk) 19:26, 17 January 2011 (UTC)
- Thanks. Even the renowned editor Malleus Fatuorum removed the hyphen from a subheading "Real vector-spaces". Agreeing that such usages are established, we can live in peace with the MOS. (I'll remove hyphens another day, then.)
- I'll read Gowers's discussion of hyphens with pleasure; I've read a couple of thoughtful and well-written essays by him already. Kiefer.Wolfowitz (talk) 19:50, 17 January 2011 (UTC)
- That was very entertaining & informative, particularly the following quote (Kiefer.Wolfowitz (talk) 19:58, 17 January 2011 (UTC)):
The author of the style-book of the Oxford University Press of New York (quoted in Perrin’s Writer’s Guide) strikes the same note when he says “If you take hyphens seriously you will surely go mad”.
Missing subtopics
When I look at this article, there are (at least) two things I'd like to find out that aren't really discussed at all.
- How are the lemma and the theorem proved? I don't know that we need a detailed rigorous proof here, but it would be good to have an outline of the main ideas, at the level that one might expect a competent grad student to be able to fill in the rest. If there are multiple proofs, how do they differ and what is their chronology?
- I comment below. A rather short proof appears in Anderson's lecture notes, which establishes a lemma implying Shapley-Folkman and Carathéodory. Howe has a conceptual, inductive proof that is probably too sophisticated to appear here. I noted proofs similar to Starr (1969), and (at risk of OR) mentioned two proofs by induction (Howe and Anderson). Kiefer.Wolfowitz (talk) 17:03, 30 January 2011 (UTC)
- How constructive is the proof? What assumptions about the sets are needed in order to compute a Shapley–Folkman decomposition of a given point in the Minkowski sum, what algorithm or algorithms are used to perform the decomposition, and how efficient is that computation?
—David Eppstein (talk) 00:00, 19 January 2011 (UTC)
- SSSSSSSSSSSHHHHHHHHHHHHHHHHHHHHHHHHHHHHH! I sent you a preprint! Kiefer.Wolfowitz (talk) 00:51, 19 January 2011 (UTC)
- Seriously, I can add a reference to a "conceptual algorithm" (really a conceptual method) of Starr. Kiefer.Wolfowitz (talk) 00:52, 19 January 2011 (UTC) Almost all of the proofs use Shapley's theory of the facial dimension, going back to his work with Karlin.
- I think the linked lecture notes by Anderson give a clean proof. I forget Howe's approach, because his other results are more interesting. Starr's approach is motivated by the idea of finding an approximation algorithm/method for the problem.
- Template:Cite article
- Sincerely, Kiefer.Wolfowitz (talk) 01:06, 19 January 2011 (UTC)
The article has improved greatly in the last weeks. Should we next try to improve it to satisfy the A-Class criteria (which are less demanding than the Featured Article criteria)? Kiefer.Wolfowitz (talk) 02:11, 20 January 2011 (UTC)
Protonk's Comments
First set of comments
- The sections "Mathematical Economics" and "Convex sets and economic equilibria" should be merged or the "Mathematical Economics" section should be expanded beyond a statement that economists were once bemused by supply and demand. :)
- In the applications section, the subsection "Math Econ" (with a short lead) contains the sub-subsection "Convex sets ...". Kiefer.Wolfowitz (talk) 04:55, 22 January 2011 (UTC)
- I did an extensive rewrite. Kiefer.Wolfowitz (talk) 17:41, 27 January 2011 (UTC)
- The "Preceding papers" section might be better moved into a short narrative history of the lemma. As it stands the article is currently broken down in a very standard (not necessarily bad) way. The mathematical basis for the lemma is asserted, the lemma itself is introduced, then applications are discussed. However the applications section is a bit curious. It reads both as applications and as historiography of progress on non-convex sets in economic theory. I think the reader might benefit if we contextualized the lemma more.
- Please review the updated version. Kiefer.Wolfowitz (talk) 17:42, 27 January 2011 (UTC)
- File:Price of market balance.gif seems largely unnecessary.
Removed.Kiefer.Wolfowitz (talk) 17:41, 27 January 2011 (UTC)
Restored, following the extensive discussion of demand sets (given prices and initial allocation). Kiefer.Wolfowitz (talk) 17:56, 30 January 2011 (UTC)
- The article overlinks quite a bit. E.g. Convex Hull is wikilinked about 7 times. Convex set is wikilinked about 6 times. And so on. An article like this demands some great linking, be it to basic concepts or more complex concepts. Without those links the article would be 3-4 times longer. But for an article of this length (about 2100 words) we shouldn't link to a concept like convex hull more than 4 times. A great test is to look at the article on a monitor of about 1200X1068 resolution and see whether or not the same blue linked word or phrase shows up more than once in the screen window as you scroll down the article.
- Thanks! I've started removing excessive links. Kiefer.Wolfowitz (talk) 04:55, 22 January 2011 (UTC)
- A note, I started this review during what appears to be a big revamp of the article. I'm going to come back tonight and take another look when it is settled down. Protonk (talk) 18:03, 20 January 2011 (UTC)
- Thanks for the great input! Kiefer.Wolfowitz (talk) 18:22, 20 January 2011 (UTC)
- I've finished my major rewrite. Some things can be expanded, but the article is rather large now. I removed the section on non-convex sets in economics that was unrelated to the Shapley Folkman lemma.Kiefer.Wolfowitz (talk) 17:41, 27 January 2011 (UTC)
- I'll take another look after class. One thing I was interested in. Do you think an animation could be helpful here? We have File:Shapley–Folkman lemma.svg, can you think of a good way to animate that to give some further illustration for the reader? I know I could do this one in R with only a little bit of work, but I'm less clear on how I could improve on the main image. Thoughts? Protonk (talk)
- I have never uploaded images. Imho, the best image would illustrate the set
- S = 1/2 ( [0,1]×[0,2] ∪ [0,2]×[0,1] )
- and then
- for N = 0, 1, 2,3, ∞. A translate of this set appears in Mas-Colell's article on non-convex sets (etc.). The sequence is the "binary expansion" of the convex hull of S. (The New Palgrave no longer contains Mas-Colell's article. I suppose one could write to him and then the publisher and ask them to donate it to the public domain.)
- Another interesting example appears early in Howe's paper, but it is not for animation.
- David's example is too complicated for animation, imho (but it is the best picture explaining the Shapley-Folkman lemma in world history, as I've asserted many times). I should learn about uploading pictures sometime. (If I could only download Polymake, then life would be easier!)
- Best regards, Kiefer.Wolfowitz (talk) 10:22, 28 January 2011 (UTC)
- I have never uploaded images. Imho, the best image would illustrate the set
- I'll take another look after class. One thing I was interested in. Do you think an animation could be helpful here? We have File:Shapley–Folkman lemma.svg, can you think of a good way to animate that to give some further illustration for the reader? I know I could do this one in R with only a little bit of work, but I'm less clear on how I could improve on the main image. Thoughts? Protonk (talk)
- I've finished my major rewrite. Some things can be expanded, but the article is rather large now. I removed the section on non-convex sets in economics that was unrelated to the Shapley Folkman lemma.Kiefer.Wolfowitz (talk) 17:41, 27 January 2011 (UTC)
Second set of comments
- Love the heuristic warning but I can't imagine it will survive FAC.
- Thanks! :) I simplified the section, which now plays it straight! ;)
- I am probably alone on this, but the LEDE image seems appropriate. I might want the caption to be a little bit shorter, but not by much.
- I shortened it. Kiefer.Wolfowitz (talk) 19:53, 22 January 2011 (UTC)
- I will try to do some of this myself, but the references section ought to be broken into a notes section and a bibliography. We cite the same paper many times at different page numbers and it would make the presentation much more clear if we did so with harvnb notation. That way individual cites to papers which only appear once can be found quickly in the references and identified by the reader. Also some of the quotes left in the references may be better moved to an explanatory footnote section or exuded entirely. Protonk (talk) 20:51, 21 January 2011 (UTC) (emboldening added by K.W., to help today's discussion and spare weak-eyed K.W. Kiefer.Wolfowitz (talk) 19:57, 1 February 2011 (UTC))
: Even the GA criteria require that each article choose either footnotes or "harvard style" (but not both). I am afraid that your suggestion would immediately threaten the GA status, and waste your time or my time, if I may worry out loud .... I trust that I am misunderstanding either the GA/FA criteria or misunderstanding your proposal .... Kiefer.Wolfowitz (talk) 19:53, 22 January 2011 (UTC) (emboldening added by K.W., to help today's discussion and spare weak-eyed K.W. Kiefer.Wolfowitz (talk) 19:57, 1 February 2011 (UTC))
- Take a look at something like The Autobiography of Malcolm X or Tulip mania as a GA and FA example of what I am suggesting. The guidance to choose one system over another exists to ensure that people don't get into fights over which is "better" and that people don't go around inserting one reference of a certain style into an article using entirely the opposite style. It is not meant as an impediment to making the references more easily accessible. In fact, the article already uses harvnb templates to point between page numbered references and footnotes which contain full bibliographic information. My suggestion is that those full bibliographic cites be placed in a separate section when/if we end up using a pointer to them in another reference. Protonk (talk) 20:33, 22 January 2011 (UTC) (emboldening added by K.W., to help today's discussion and spare weak-eyed K.W. Kiefer.Wolfowitz (talk) 19:57, 1 February 2011 (UTC))
- That's very re-assuring, and makes sense. I'll try to work on content first, and gradually start the transition, as you suggested. I think that the economics section needs more explanation, as the biggest priority. Kiefer.Wolfowitz (talk) 21:11, 22 January 2011 (UTC)
- I reformatted the references following your advice, and the featured-articel on Tulip Mania, which you suggested. Thanks again!
- It would be good to go through Starr's article and ours again. I provided page numbers to every citation.) Kiefer.Wolfowitz (talk) 05:02, 25 January 2011 (UTC)
- That's very re-assuring, and makes sense. I'll try to work on content first, and gradually start the transition, as you suggested. I think that the economics section needs more explanation, as the biggest priority. Kiefer.Wolfowitz (talk) 21:11, 22 January 2011 (UTC)
- Take a look at something like The Autobiography of Malcolm X or Tulip mania as a GA and FA example of what I am suggesting. The guidance to choose one system over another exists to ensure that people don't get into fights over which is "better" and that people don't go around inserting one reference of a certain style into an article using entirely the opposite style. It is not meant as an impediment to making the references more easily accessible. In fact, the article already uses harvnb templates to point between page numbered references and footnotes which contain full bibliographic information. My suggestion is that those full bibliographic cites be placed in a separate section when/if we end up using a pointer to them in another reference. Protonk (talk) 20:33, 22 January 2011 (UTC) (emboldening added by K.W., to help today's discussion and spare weak-eyed K.W. Kiefer.Wolfowitz (talk) 19:57, 1 February 2011 (UTC))
- I am not an expert at reference formatting expectations for FA, but I think direct quotes from sources should be provided where the sourced statement demands some additional verification and the source material is not freely available. Protonk (talk) 20:51, 21 January 2011 (UTC)
- I don't think that there is anything controversial in the article, so I doubt that this is a concern. (I changed the Borwein/O'Brein reference so that it became an secondary citation (via Schneider); the paper is inaccessible unless you have a good librarian or write Borwein's secretary.) All the remaining sources should be readily available to members of universities or even good colleges, who usually have to pay a club-fee tuition or subsidies indirectly. Is that what you mean by free? Kiefer.Wolfowitz (talk) 19:53, 22 January 2011 (UTC)
- I'll try to articulate this a bit. A common practice (not widespread, but common enough) for FA class articles where there is some difficult to access source is to include a paragraph excerpt in the footnote of a particular claim. So if I am writing an article on the Idaho Falls nuclear accident and I cite a claim to the commission's report on the incident I might want to include a quote in the footnote itself so that someone perusing the article can see how close or far my paraphrasing was from the original content. I do this partially because the commission's report on Idaho Falls isn't exactly easy to get at and because I may be inserting a strong claim into the article. By contrast an article like this may not require such excerpting. On a closer review of the references I only see a few long parenthetical notes or excerpts so this isn't a bit deal. Protonk (talk) 20:33, 22 January 2011 (UTC)
- Whew! That's a relief! I suppose that some French titles and Lemaréchal's preprint are hard to get, I had to ask him for it. But his preprint was cited by Ekeland directly and vaguely, so I don't think that it is a problem either. But your suggestion makes sense, and goes with the prime directive of writing to help the readers. Kiefer.Wolfowitz (talk) 21:11, 22 January 2011 (UTC)
- Thanks for the examples: Emulating the FA tulip mania is easier than memorizing the MOS. I'm beginning to implement the suggested changes. I'll update the hyperlinks of the form [3] after I've moved all the important references below. (Pardon the day or so of inconsistencies or redundancies in referencing, please.) Thanks again! Kiefer.Wolfowitz (talk) 23:28, 24 January 2011 (UTC)
- Whew! That's a relief! I suppose that some French titles and Lemaréchal's preprint are hard to get, I had to ask him for it. But his preprint was cited by Ekeland directly and vaguely, so I don't think that it is a problem either. But your suggestion makes sense, and goes with the prime directive of writing to help the readers. Kiefer.Wolfowitz (talk) 21:11, 22 January 2011 (UTC)
- I'll try to articulate this a bit. A common practice (not widespread, but common enough) for FA class articles where there is some difficult to access source is to include a paragraph excerpt in the footnote of a particular claim. So if I am writing an article on the Idaho Falls nuclear accident and I cite a claim to the commission's report on the incident I might want to include a quote in the footnote itself so that someone perusing the article can see how close or far my paraphrasing was from the original content. I do this partially because the commission's report on Idaho Falls isn't exactly easy to get at and because I may be inserting a strong claim into the article. By contrast an article like this may not require such excerpting. On a closer review of the references I only see a few long parenthetical notes or excerpts so this isn't a bit deal. Protonk (talk) 20:33, 22 January 2011 (UTC)
Economics applications
- Pay special attention to the section titled "Non-convex sets in contemporary economics". The first paragraph is nearly all a quotation, the second paragraph is a mass of blue links (there to support the claims of the first paragraph) and the third paragraph is an attempt at contextualization which doesn't completely succeed. The thesis of the section is that Shapley & Folkmann (and later Starr) influenced mid 20th century mathematical economics by expanding the bounds within which optimizing agents could be used to describe an economy. they did this by showing that convex hulls could be operated on with non-convex preferences if the number of agents exceeded the dimensionality of the problem (basically). The section itself should clearly lay this out by first presenting the problem of non-convexity of preferences and picking salient examples where economic analysis was unable to provide clear answers prior to Starr's work. Then you can give a very brief precis of how the work allowed economists to reach a solution. This may seem clear to you but picture a hypothetical educated reader interested in economics but unable to see immediately where the limitations exist and why they are important. the benefit of restructuring this section is that you can probably fold in some of the "Convex sets and economic equilibria" parts. As it stands the explanation is that convexity allows us to exploit the fixed point theorem. That's great, but I would submit a large number of readers don't know the fixed point theorem or can't explain all of its implications (AMM had a great interview with a mathematician who surveyed faculty at various math departments and found that only a small minority said they could prove the fixed point theorem--I have lost the PDF but I will try to find it). Protonk (talk) 22:12, 21 January 2011 (UTC)
- I worked on the economics: Please consider helping! I removed the paragraph on non-convexity unrelated to the Shapley-Folkman lemma, because the article has 78 K, and 80+K triggered warning messages. Kiefer.Wolfowitz (talk) 12:51, 26 January 2011 (UTC)
- Reformatting and removing redundancies in the notes reduced the article from 78 to 72 K. Kiefer.Wolfowitz (talk) 18:56, 26 January 2011 (UTC)
- I did a major rewrite of the economics, providing the context. The convexification of preferences is much older than indicated previously. Following Diewalt, I cite Wold. I also provided references to Lyapunov's theorem, Vind (1964) and then Aumann.
- I shall look another day at providing more narrative: However, I am afraid of OR violations if I give too much of a narrative. The previous versions made Starr's paper a work of genius. The present writing makes his approach a natural development, following Wold, Farrell & Rothenberg, Vind, Aumann, Shapley & Shubik, etc. Starr and Arrow/Hahn certainly credit all of these (but Wold). Kiefer.Wolfowitz (talk) 18:02, 30 January 2011 (UTC)
Images
- There are also a few too many images in this article. I would drop (in ascending order of importance to the article): File:Kenneth Arrow, Stanford University.jpg, File:Unit circle.svg, and the pair File:Convex polygon illustration1.png File:Convex polygon illustration2.png. The last set might stay in because they give a concise graphical explanation of both what a convex set is and how to test for convexity, but they aren't absolutely critical. I would also differentiate the various reuses of File:Shapley–Folkman lemma.svg visually. At time of writing it is used 4 times in the article to illustrate the basic idea of the lemma and three steps along the way. Each of the three steps might be better served by some coloring of points differently or otherwise a stronger visual hint to the reader. Otherwise we don't gain much by seeing them again.
- David Eppstein created another great graphic, better distinguishing the circum-radius and inner-radius. (However, I still think that his original graphic should be savored.) Kiefer.Wolfowitz (talk) 05:07, 22 January 2011 (UTC)
- Regarding pictures, I'd ask for a third opinion: I heard Victor Lomonosov lecture on his (juvenalia) invariant-subspace theorem (which used Schauder's generalization of Brouwer's theorem), and he drew a picture (5 seconds). (I recognize that my feelings are strong here: My mind is very geometrical, and so I like pictures. Also, Ken Arrow is a hero & mensch, and seeing his picture gives me a warm feeling, honestly.) Kiefer.Wolfowitz (talk) 05:07, 22 January 2011 (UTC)
- I love pictures myself, and econ concepts generally don't produce too many. But keep in mind that the page is going to get visually crowded quickly and soon you will have to be making decisions at the margin about where to position pictures and which may be removed. Protonk (talk) 05:59, 22 January 2011 (UTC)
- I also love pictures and think that too many is better than too few. But I suspect that using the same one three times is probably suboptimal. If you want to refer to it from later text, why not just refer to it? —David Eppstein (talk) 06:53, 22 January 2011 (UTC)
- (Having learned to program with Pascal and having read Dijkstra's "Notes on programming", I like to reduce cognitive demands at all times! ;) The short captions focused on different aspects of the picture, which illustrated the nearby text. Kiefer.Wolfowitz (talk) 08:55, 22 January 2011 (UTC))
- Your comment about the budget of article size (especially pictures) was correct. The article is at 78K, and 80+K generated warning messages about length. I removed some stuff, which is stored on this page. Kiefer.Wolfowitz (talk) 12:53, 26 January 2011 (UTC)
- Apologies that these comments are nearly exclusively non-mathematical. I'm the sort of economist who shies away from talking about the finer points of set theory and measure theory due to a severe skill deficit. :) Protonk (talk) 01:09, 22 January 2011 (UTC)
- You've done a great job! (K.W.)
Revamping: Inner radius and optimization
User:Protonk noted that I was making a major revamp of the article.
David's sumset graphic
I recognized that David's graphic sufficed for an explanation of the inner radius and the circumradius, so I re-used it with another caption. Kiefer.Wolfowitz (talk) 18:22, 20 January 2011 (UTC)
- It will do for now but I can produce a more targeted graphic later. (Probably not today, I have a conference submission deadline looming.) —David Eppstein (talk) 18:28, 20 January 2011 (UTC)
- Tell me about it! ;) I would have thought you were used to it by now. Good luck on your conference. Let other people patrol the NP and P page while you work on the submission.
- It would be useful to have an example of non-convex preferences, and then give an example of summing them, and showing the approximate decrease in non-convexity. Now, the economics doesn't provide motivation and insight into the mathematics. I would suggest using the example from the Shapley-Shubik article, which is the max of two Leontieff functions.
- (Maybe it would be original research to make up an example of a zoo-keeper deciding between one lion and one eagle, and being bummed because no griffin be available!) Both Shapley-Shubik and Starr (1969) have clear and interesting examples to drive home the idea that non-convexities are important.
- Best regards, Kiefer.Wolfowitz (talk) 19:39, 20 January 2011 (UTC)
WOW! David produced another great graphic. (BTW, I simplified the captions and used his earlier picture a few times.) Kiefer.Wolfowitz (talk) 05:09, 22 January 2011 (UTC)
Optimization
I tried to make the Optimization section intelligible to a reader who remembered the definition of the Euclidean metric from a sophomore course in linear algebra (USA). I added pictures of convex functions, using the epigraphal definition for simplicity (and maximum connection with the earlier sections), rather than tangential or secant criteria.
I took the risky decision to give a heuristic description of Ekeland's analysis first, and then give the truth (with another slew of topological notions). I would appreciate feedback, and probably damage control from other editors. (Rockafellar and Ekeland/Teman or Ioffe/Tickhomirov have the main results in accessible form: I consulted Ekeland for the lsc equivalence with a closed epigraph). Sincerely, Kiefer.Wolfowitz (talk) 18:22, 20 January 2011 (UTC)
- Editor Protonk commented above.
- I shall continue to edit the optimization section, aiming for additional simplifications. Kiefer.Wolfowitz (talk) 21:08, 21 January 2011 (UTC)
- I simplified it as much as possible, focusing on the SF lemma, and down-playing the (human interest story about the) young mathematicians Lemaréchal and Ekeland. I should probably cite Bertseka's Lagrange-multipliers book more, which is rather similar to Ekeland's appendix. I should add page numbers to Rockafellar's "bible", which gives an unbounded closed set and bounded closed set having a sum that is not closed. Kiefer.Wolfowitz (talk) 05:14, 22 January 2011 (UTC)
Comments
I'll break up the comments, to lessen the head-aches with edit-conflicts in the future. Kiefer.Wolfowitz (talk)
Lead
I think the article is too inaccessible for a general reader. I don't think it needs to be. But it is. At a minimum, would work on the lead so that it is more helpful to a general reader. So he can get more feel for the topic even if he is not going to slog through the meat of the article (or really all the other articles he has to read to understand this one).
- I really appreciate your suggestion, which raises the same accessibility concern as Geometry Guy (whose concern I had discounted before because I was having trouble imagining him reading like a civilian!). To reduce clutter, I'll only thank you here for some of the related and often more detailed comments on the lead below, which I really appreciate. Kiefer.Wolfowitz (talk) 09:18, 8 February 2011 (UTC)
-I like the circle and disk thing, that was very clear.
-Wonder about having so many equations in the lead. Is there some what to trim how many there are? Think of the lead as a version that should be helpful to even the non math grad students.
- I moved some of the equations into the introductory example section, following your complaints and Geometry Guy's suggestion. Kiefer.Wolfowitz (Discussion) 20:54, 22 February 2011 (UTC)
"Euclidean" distance
-Don't specific the "Euclidan" (blue-linked) distance in the lead. If you feel the need, specify that in the text, but for the lead, Euclidian distance is exactly normal distance anyhow.
- DONE!
Set and interval notation
-not sure the answer, but presenting intervals in brackets and then sets in braces, is a little tricky for the average reader. It took me a bit before I noticed what you were doing. Remember he is grappling with new material, so notation makes it that much tougher. And braces and brackets are similar looking This is one reason why the graphical circle and disk are nice. Perhaps you could make the point by using a number line or some such, to show endpoints versus segments.
- In the lead, I had neglected to preface the set {0,1} with "the set of integers" and to preface the interval [0,1] with "interval of real numbers". I hope that the lead is now self-contained regarding set and interval notation. Kiefer.Wolfowitz (talk) 15:57, 8 February 2011 (UTC)
-Minkowski explanation was good and helpful.
- Thanks! Kiefer.Wolfowitz (talk) 15:57, 8 February 2011 (UTC)
SF lemma versus theorem
-I have a hard time in the lead keeping track of the lemma versus the theorem (both in terms of what is what in math, and also what was published when). Also a bit confusing that the title is one of them, but the discussions moves to the other rather quickly. And just the structure of why we talk about one versus the other and when.
- Others have commented on that the distinction between lemma and theorem is cognitively taxing. Fixing this problem would require a change of terminology, which would be original research unless it followed a reliable publication. Kiefer.Wolfowitz (talk) 10:07, 8 February 2011 (UTC)
- Worse, the literature (even Starr!) often calls Starr's corollary the SF theorem, and calls the SF lemma the SF theorem. O tempes... Kiefer.Wolfowitz (talk) 10:07, 8 February 2011 (UTC)
Image and "cover"
-lead image, caption. Do we have the use the "cover" term in the lead? I guess it is some exact term for congruency or such, but I worry that it's a bit like "Euclidean distance". Again if we can be simpler in the lead, we can always still have the rigor in the main article.
- "Cover" is the geometric term for "contain" (in set theory). I'll use "is a subset of" consistently, to make it more accessible. (There is sometimes confusion about colloquial containment, versus subset-inclusion, notably with the circle: In everyday English, the line segment connecting two points of a circle is "contained in" the circle! The change avoids that confusion.)
Lyapunov theorem on vector measures
-Lyapunov thing: Not 100% clear the value of saying that SF is related to it, in lead. Seems like we are just saying one strange concept is related to some other, strange and bluelinked concept (And by the way, when I go to that blue link, it doesn't help me know what Lyapunov is about, is very skimpy.) Did Lyapunov come before or after? Are they parallel discoveries under different concepts (as for instance some aspects of options theory, really are the same thing as insurance?)
- Following your suggestion, I removed it from the lead. Kiefer.Wolfowitz (talk) 15:08, 8 February 2011 (UTC)
- I added the short section on Lyapunov's theorem on the article on vector measures. I am sorry that my time does not allow me to expand it further. Kiefer.Wolfowitz (talk) 09:18, 8 February 2011 (UTC)
Applications in lead
-Has this thereom helped anyone practically (it's OK if no, just asking). I mean have people made factories run faster, built bombs, decoded ciphers, learned genetics, etc. from it? Can we push for some tangible explanation of the economic or practical impact of the theorom?
- I have a conflict of interest that prevents me from answering honestly and directly: I have a paper being refereed on computations and practical implications: At risk of OR (which I hope may be pardoned in a talk page), I can say that the lemma, when viewed properly, has such implications and applications. It is true that knowledge of the SF lemma has encouraged applications in large scale optimization, following Lemarechal, Ekeland, and Bertsekas: Engineers "know" that Lagrangian dual methods "work" on separable problems that are non-convex---contrary to the advice of an otherwise leading classic textbook of Gill, Murray, and Wright. The Bertsekas article in IEEE transactions has been cited hundreds of times. Kiefer.Wolfowitz (talk) 09:18, 8 February 2011 (UTC)
-don't bother wikilinking statistics.
- Linking to the profession of mathematical statistics is useful for disambiguation: otherwise, people think of accounting and official statistics. (I am a statistician, and have some professional obligations to give statistics its due.) Kiefer.Wolfowitz (talk) 10:54, 8 February 2011 (UTC)
Graphics
-Image caption: what does sum of two original sets and two convex hulls mean? You mean all 4 added together?
- Yes. The four sets on the left are summed, yielding the sum on the right.
- David's graphic doesn't use coordinates, which would require more ink. Also, Minkowski addition is affine invariant, which means that the choice of coordinate system doesn't matter, so it is mathematically better to avoid coordinates. It may be that civilian readers would be helped by coordinates: The zero vector could be marked in each window.
-Same image lower down: do we really need to show four sets or would two work to show the concept? Just trying to make it that much easier to grasp. I don't understand what the plus signs are doing. How are the four left sets nonconvex? Are they individually non convex? When they are just line segments?
- Two sets would exhibit the commutativity of Minkowski addition and convexification. Three sets would suffice to display the Shapley-Folkman lemma. However, having 3 sets on the left would be uglier, because 1x3 or 3x1 doesn't harmonize with the right-hand summed set. David's2x2 pane is the best, imho. He is also an internationally recognized computational geometer, and his judgment about presenting visual information should be afforded the greatest consideration. His use of pink for the convex hull of the red points is natural and beautiful, so that I wonder that nobody thought of it before (at least in connection with the SF lemma). Kiefer.Wolfowitz (talk) 10:07, 8 February 2011 (UTC)
Containment, in mathematics versus vernacular
-I would be careful about using the term "contain" wrt to the line segment on the inside of a circle. I get what you mean about the points on the interior not being a part of the set of points in the circumference. Just when you look at a segment, it's contained in the sense that it's inside the boundary. Just not contained in the set. Not sure how to fix this, but just be aware of how this throws people.
- I removed "cover" and "contain" and used only "subset" in the lead. Kiefer.Wolfowitz (talk) 10:07, 8 February 2011 (UTC)
Indifference curves
-I actually kinda know what an indiffernce curve is, but I struggled with the discussion here in article. Is it really necessary to talk about it in terms of a basket of goods (guns butter, blabla) versus a simple example using currency? Also "vector"? I'm sure that's math econd talk and thinking of things that way helps. But I learned econ without having to think of it s a "vector", but just some curve (functional relationship).
- Money is one of the most difficult parts of economic theory, and so I would avoid currency. (BTW, Starr is an expert on money in general equilibrium theory.)
- The article had previously discussed vectors, so I thought it most natural to continue using the vector terminology. However, your comment here, as previously, deserves thought. I have difficulty editing this week and possibly next week. But in 2 weeks I'll make another editing push on the article. Kiefer.Wolfowitz (talk) 10:07, 8 February 2011 (UTC)
-what are the axes of the curve with the Pareto front thing zooming around? and what is with the tangents to the curve and the perpindicular to the tangent zooming around?
- I'll ask the up-loader to remove the distracting text from the image, per Wikimedia guidelines. The graphic was designed to show vector-valued optimization, but it works for univariate optimization for one consumer with non-convex preferences. Kiefer.Wolfowitz (talk) 10:07, 8 February 2011 (UTC)
-"Taking the convex hull of non-convex consumer preferences had been discussed earlier by Wold." So? So what?
- This is noted by Diewert, I believe, not having that reference available today: I gave the page reference. Shapley-Shubik took convex hulls of preferences, as did Starr. Unless Wold is mentioned, the article suggests that Shapley-Shubik's re-invention of convexification were original, contrary to fact and surveys like Diewert. (The intellectual juggernaut Wold deserves remembering, here and in connection with time series analysis and causality & observational studies, etc., I have insisted---noting that Wold was the professor of statistics at two Swedish universities, one being mine! RE: COI concerns!)
- DONE! (I moved the Wold priority information to a footnote.) Kiefer.Wolfowitz (Discussion) 20:24, 14 February 2011 (UTC)
Discussion, quoted by Volunteer Marek below
-It makes me very happy to see the crossed linear supply and demand curves. Happy to see something I know. that;s not so "hard". But connection to the article?
- To understand Starr's economics, one must know that supply and demand are functions of prices, and that the problem is to establish the existence (etc.) of an equilibrium price vector---with good properties (efficiency) for convex sets.
-Maybe if you can more explicitly have a para saying who came up with what, when in what paper (Shapley, Folkman and Starr), that would be good. I mean just reporting who got academic credit even. It just seems confusing when mixed with actually elaboration on the concepts themselves. -Is the whole shebang basically telling me that if we have a lot of zookeepers, we can effectively think of half a lion and half an eagle as the euqivlaent of a single lion or single eagle (like it all comes out in the wash with a lot of actors?)
- The zoo-keeper example is good for explaining a concavity in preferences, but I suspect that an everyday example would be better for explaining the economic consequences of the SF lemma.
- In this case, the dimension is two. For 3 or more zoo-keepers, for a given price, the aggregate demand (or a fixed demand, if uniqueness fails) of the convexified economy is exactly the sum of two convexified demands, and one possibly non-convex demand. This aggregate demand is closely approximated by the sum of three possibly non-convex demands. Kiefer.Wolfowitz (talk) 10:56, 8 February 2011 (UTC)
Significance?
-Was there like a big edifice waiting for Starr and SF to prove their theorems? I mean like there are parts of math that rely on Reimann hypothesis being true and if it's ever disproven they will come crumbling down (or the converse will be confirmed as that is sole uncertainty they rely on)?
- Many economists have written that the SF lemma and SFS theorem are surprising, and that it's a disappointment that these results are little known outside of mathematical economics.
- As OR, I can state here that the published literature lacks any claim that the SF lemma has any such importance in mathematics. Kiefer.Wolfowitz (talk) 10:59, 8 February 2011 (UTC)
-How much of a big deal was it (is it) that SF and S have this theorem/lemma? Is it like Andrew Wild Fermat's Last Theorem famous?
- Any speculation would be OR. Many mathematicians don't care about Fermat's last theorem, and believe that Wiles's spectacular achievement is most important because of its advancement of number theory (and related areas of Diophantine geometry).
- This is usual in mathematics. For example, von Neumann's theory of Hilbert space and related operator theory are important for their own sakes, only partially because they resolved a disagreement between two schools of physics.
- In practice, I suppose that Bertsekas's use of Lagrangian dual methods on large separable primal problems (with many non-convex summands) is partially related to his knowledge of the SF lemma (via Ekeland or via Aubin & Ekeland). I suppose that hundreds of IEEE papers cite Bertsekas's paper on scheduling. (On the other hand, Lemarechal learned all he need to know from Lasdon's 1970 book on large scale optimization, which was reprinted a few years ago by Dover. Thus, I would not want to claim that the SF lemma has had a huge impact on practice.) Kiefer.Wolfowitz (talk) 11:03, 8 February 2011 (UTC)
- Intellectually, the biggest impact has been on economics. Economists no longer claim that convexity is essential market-clearing or efficiency in large economies. Even Varian's intermediate microeconomics book has some vague discussion of the convexity of sums of non-convex sets. Kiefer.Wolfowitz (talk) 11:03, 8 February 2011 (UTC)
-How hard was it for them to prove this stuff (like how many equations, how long a paper, how many different aspects of math brought in)?
- Their memo is only a couple pages of length. Economists, like Arrow and Hahn, spend more time proving things. However, the literature lacks a survey or analysis of proofs, although some economists have lamented the (perceived) complications of proofs, so discusing this would be OR. Kiefer.Wolfowitz (talk) 11:03, 8 February 2011 (UTC)
Mathematical style
-"which we define" Who's we?
- "We" is conventional in mathematics and sanctioned by the WP manual of style for mathematics. Perhaps this can be changed. Kiefer.Wolfowitz (talk) 11:05, 8 February 2011 (UTC)
- I guess it's allowed. It just seems a little jarring, given the rest of the depersonalized style Wiki (or rest of article) is in. And even in your article, here, you used it like once (that I noticed). Not sure it's really needed, not a long proof or whatever. Note, my point is not some "follow the rules" officiousness. It's more of an artistic one. The term made me skip a beat (as general reader). And of course the objective is to make things smoooooth for the reader. Not have him hesitate. No big deal, really, though. ;-) TCO (talk) 20:13, 8 February 2011 (UTC)
-closure of a set. I think I got the beginning of this discussion but kinda lost track of the point as it finished.
- The sum of closed sets need not be closed. That's why Ekeland had to add the closure operator. However, most people won't need or understand the closure operator, so the background information on closed sets follows the application by Ekeland. Kiefer.Wolfowitz (talk) 11:05, 8 February 2011 (UTC)
-I don't know what a summand is or what dimension is? But can these terms be avoided in the lead? Perhaps used in the body for rigor? IOW can the key concept be explained without getting into them, at first?
- Summand is the object being summed. For example, in the expression "1+2", the numbers "1" and "2" are summands.
- Dimensions 2 and 3 should be familiar from sophomore geometry, which used to be required by many states in the US, e.g. Ohio, so should be expected of WP readers imho. Defining (higher) "dimension" would require more linear algebra, which would make the lead less useful. Kiefer.Wolfowitz (talk) 11:05, 8 February 2011 (UTC)
Coda
Sorry, that's the best I can do, at present. Good luck with it. If you want to leave it an article for math-econ grad students, won't bug me. Just giving you my reaction as I try to read it.TCO (talk) 01:06, 8 February 2011 (UTC)
- Your contributions have been most valuable. What was most needed was feedback from an experienced WP editor (with excellent copy-editing skills) who was not a mathematical scientist or economist. I am very grateful. I shall have to delay responding to most of the concerns for a week or two, unfortunately, due to professional commitments. Thank you again for the detail and clarity of your questions, which will be very helpful in guiding revision. Best regards, Kiefer.Wolfowitz (talk) 11:06, 8 February 2011 (UTC)
Wisdom from Volunteer Marek

I'm gonna butt-in again. Here:
-It makes me very happy to see the crossed linear supply and demand curves. Happy to see something I know. that;s not so "hard". But connection to the article? (TCO)
To understand Starr's economics, one must know that supply and demand are functions of prices, and that the problem is to establish the existence (etc.) of an equilibrium price vector---with good properties (efficiency) for convex sets. (KW)
Since Starr's contribution was in relation to general equilibrium wouldn't an Edgeworth box (with a price tangent line/separating hyperplane) be more appropriate than a single market supply/demand diagram? The animated graphic's pretty sweet though. Volunteer Marek 10:24, 8 February 2011 (UTC)
- I agree. Edgeworth box = General equilibrium, whereas Crossed Supply and demand curves = Partial equilibrium --Forich (talk) 00:17, 17 February 2011 (UTC)
- On the one hand, your comments are correct. On the other hand, Starr's economics deals with adding demand-functions , and so the demand-function is needed. The linear demand-function is the simplest for a picture. Let me look at the article on the Edgeworth box. (I made minor edits to the others' comments.) Kiefer.Wolfowitz (Discussion) 20:59, 22 February 2011 (UTC)
Griffin example
-Is the whole shebang basically telling me that if we have a lot of zookeepers, we can effectively think of half a lion and half an eagle as the euqivlaent of a single lion or single eagle (like it all comes out in the wash with a lot of actors?)
It sort of means that if we have a lot of zoo keepers then there will be prices (a price for lions and eagles) at which every zookeeper chooses his optimal combination of lions and eagles and at which the total supply of eagles "almost" equals the total demand for eagles and same for lions. The lemma also tells you what this "almost" means ("almost" could be "exactly" in special cases) (I think). Volunteer Marek 10:37, 8 February 2011 (UTC)
does the "hull" contain the originating set itself?
In which case you could say the sum of the two hulls, instead of sum of the two hulls and two sets?TCO (talk) 20:06, 8 February 2011 (UTC)
- Hi TCO, the convex hull contains the original set and convex combinations of its points.
- I suspect that there might be some misunderstanding, so let me try to explain David's graphic, for a minute.
- On the left, There are four sets being summed, each of which contains exactly two points. Taking the convex hull of the two of the points in a summand creates a line segment. These four summands are shown in the left pane.
The right pane displays the sum of the four sets, which consists of 16=2(raised to the 4th) red dots, all the possible sums of the points in the sets. (Sorry, I have to run.) Kiefer.Wolfowitz (talk) 20:27, 8 February 2011 (UTC)
I know it's your peice de resistance. But I still have to peck at it.
- Keep the questions coming! They are helpful! :-)
- If the convex hull contains the originating set, why do we talk about adding "two sets and their convex hulls". Why not just adding the convex hulls?
- The surprising thing is that for a given point, you need add the convexified versions of only two summand-sets! You then add the other two original summand-sets!
- Also, why show four line segments but talk about adding two of them in the caption?
- Maybe an "a" and a "b" for the two sides of the diagram would be helpful.
- I think it should be clarified in the "a" caption that the originating set is the end points and the convex hull is the line segment.
- I still don't know why we have to have four of them instead of two (on the a side). Even if you need three, might be simpler. Yeah, you have a little unused space on the A side, but it just makes the number of points on the b side a little simpler.TCO (talk) 23:05, 8 February 2011 (UTC)
- Thanks! I'll write more in the next week(s).... Kiefer.Wolfowitz (Discussion) 21:18, 22 February 2011 (UTC)
Comments on splitting off Shapley-Folkman-Starr theorem?
The only way to improve this article to FA status seems imho to require removing the material on the Shapley-Folkman theorem and Starr's corollary to it, which would then be transferred to a new article on the SFS theorem. When I floated this idea on the Peer Review page, Geometry Guy suggested that such a split-off would improve the summary style of the article. David Eppstein also liked the proposal and suggested that the name "SFS theorem" would be better than "Starr's theorem" or "Starr's corollary to the SF theorem".
Please comment! Thanks! Kiefer.Wolfowitz (Discussion) 00:18, 2 March 2011 (UTC)
The previous discussion followed Ekeland's notation, using the closure of a set. Sequential convergence allowed an elementary treatment: The need to consider the closure of a set is noted in the footnote. Kiefer.Wolfowitz (Discussion) 15:54, 5 March 2011 (UTC)
- This revision is discussed at User talk:Kiefer.Wolfowitz#Monty Hall problem: WP:ArbCom with concern to distinguish original research and original exposition, when following wikipedia OR policy.
- It is jarring for me to read "For example, ... For a separable problem, we consider an optimal solution ... For a separable problem, we consider an optimal solution ..." Maybe say "Given a separable problem". --P64 (talk) 18:22, 9 April 2011 (UTC)
- That's a good suggestion. Thanks for your thoughtful comments and again thanks for alerting WP editors about the discussion on my talk page. Kiefer.Wolfowitz (Discussion) 11:57, 10 April 2011 (UTC)
- ^ The Arrow-Debreu model continues to be studied in economics research and to be taught in graduate courses in microeconomic theory.
- ^ Starr (1969, p. 25)
- ^ Cite error: The named reference
Blahwas invoked but never defined (see the help page).
The article gives an example, stating the measures be defined on the same probability space. This is sloppy: they should be defined on the same finitely measurable space (that is a space with a sigma algebra on which a finite measure is definable). Kiefer.Wolfowitz 17:51, 29 September 2011 (UTC)
In advanced measure-theory, the Shapley–Folkman lemma has been used to prove Lyapunov's theorem, which states that the range of a vector measure is convex.[1] Here, the traditional term "range" (alternatively, "image") is the set of values produced by the function. A vector measure is a vector-valued generalization of a measure; for example, if p1 and p2 are probability measures defined on the same measurable space, then the product function (p1, p2) is a vector measure, where (p1, p2) is defined for every event ω by
- (p1, p2)(ω)=(p1(ω), p2(ω)).
- ^ Tardella (1990, pp. 478–479): Tardella, Fabio (1990). "A new proof of the Lyapunov convexity theorem". SIAM Journal on Control and Optimization. 28 (2): 478–481. doi:10.1137/0328026. MR 1040471.
{{cite journal}}: Invalid|ref=harv(help)
Nobel Prize in Economics: Increased readership
I identified Nobel laureates associated with non-convex sets and also convex sets. Most of these have been mentioned in association with linear programming; many have already been discussed here (Arrow, Debreu, Samuelson, Koopmans, Aumann, etc.). Krugman received the prize for his work on increasing returns, which is a topic of non-convexity in economics (discussed e.g. by Partha Dasgupta).
One effect of the Nobel prize identification should be an increased readership, particularly if this page be featured on the 10th (of October) this year, when the Nobel Prize is announced. Kiefer.Wolfowitz 14:11, 3 October 2011 (UTC)
Draft lede for front page
I trust that the article should soon receive FA status,
- I just HAD to open my big mouth! Famous last words! (KW 14:04, 8 October 2011 (UTC))
and so I started drafting a main-page lede. I favor the blue graphic, because the primary graphic with its 5 panes does not appear well at 100 pix.
Kiefer.Wolfowitz 13:58, 4 October 2011 (UTC)
In geometry and economics, the Shapley–Folkman lemma describes the Minkowski addition of sets. Lemmas are steps in a mathematical proof of a theorem. Minkowski addition is defined as the addition of the sets' members: for example
- {0, 1} + {0, 1} = {0+0, 0+1, 1+0, 1+1} = {0, 1, 2}.
The Shapley–Folkman lemma provides an affirmative answer to the question, "Is the sum of many sets close to being convex?" A set is defined to be convex if every line segment joining two of its points is a subset in the set: For example, the solid disk is a convex set but the circle is not, because the line segment joining two distinct points is not a subset of the circle. The Shapley–Folkman lemma suggests that if the number of summed sets exceeds the dimension of the vector space, then their Minkowski sum is approximately convex. The lemma has many applications in economics, where non-convexity is associated with market failures, that is, with inefficient or non-existent economic equilibria. Non-convex sets have been studied by many winners of the Nobel Prize in Economics: Arrow (1972), Aumann (2005), Debreu (1983), Hurwicz (2007), Kantorovich (1975), Koopmans (1975), Krugman (2008), Samuelson (1970), and Solow (1987). (more…)
Nonconvexified versus unconvexified
This article uses "unconvexified", following our masters: Boris Mordukhovich's Variational analysis and generalized differentiation and Terry Rockafellar's and Roger Wets's Variational analysis.
The alternative "nonconvexified" is non grata.
Kiefer.Wolfowitz 18:04, 7 October 2011 (UTC)
Featured article issues
The featured-article review elicited many good suggestions, which I was able to act upon to improve the article.
Additional suggestions were made that needed additional time to address. These suggestions are copied here for ease of reference. Kiefer.Wolfowitz 11:28, 5 November 2012 (UTC)
The following discussion is closed. Please do not modify it. Subsequent comments should be made on the appropriate discussion page. No further edits should be made to this discussion.
Weak oppose. Let me first add to the praise above for the meticulous work that has gone into this well-referenced and carefully explained article on an important technical topic. The article has much improved since February (where I contributed a partial peer review). Nevertheless, on reading the article closely (having not done so since February), I find that it falls short of the demanding FA criteria in several respects, and so cannot support its promotion at present. Areas where I believe improvements could be made include: clarity of exposition, engaging/brilliant prose, comprehensiveness and organization. I will add detailed remarks shortly, most of which I hope can be easily addressed. Geometry guy 21:41, 7 October 2011 (UTC)
- I thank you for your past comments. I shall address whatever suggestions you make to the best of my ability. (I am away from my office until next week, however.) Kiefer.Wolfowitz 22:08, 7 October 2011 (UTC)
- Leading issues. The first few sentences of the lead already illustrate some of the issues (numbered so that it should not be necessary to interleave replies).
- The repetition "In geometry and economics... In mathematics..." is clunky; despite comments made above about readers not knowing what a lemma is, an entire sentence is overkill – why not simply wikilink "Shapley-Folkman Lemma"?
- The article does not explain what the Shapley-Folkman-Starr theorem is: it discusses their results, including a Shapley-Folkman theorem and Starr's corollary, but no theorem with that name.
- The lead sentence does not define the topic: the Shapley-Folkman(-Starr) results do not describe the Minkowski addition of sets in a vector space (the definition of Minkowski addition does that); they describe the extent to which the Minkowski sum of many sets is approximately convex.
- The distinction between "addition" and "sum" is important. "Addition" is a synonym for "summation", the process of adding, not a synonym for "sum", the result of the addition. (We do not say "5 is the addition of 2 and 3".) The lead needs to make this distinction clear for Minkowski addition/sums, so that the terms can be selected and used for maximum clarity in the article.
- The lead uses terms such as "summand(-)set" and "sumset" without defining or wikilinking them. A particularly problematic example is "average sumset". I was completely unclear about what this meant until I read section 3.2.
- Theorems do have ("hypotheses" and) "conclusions", and I am relaxed about the idea that a theorem may "address" or "concern" a particular question. "The Shapley–Folkman–Starr results suggest..." is a bit too loose for me, however. A naive reviewer might ask "suggest to whom?", but the point of the sentence is to provide an intuitive summary of the results, not make suggestions.
- "The Shapley–Folkman–Starr theorem states an upper bound on the distance between the Minkowski sum and its convex hull—the convex hull of the Minkowski sum is the smallest convex set that contains the Minkowski sum." Unnecessary repetition: "its convex hull (the smallest convex set containing it)".
- "Their bound on the distance..." Antecedent missing/unclear.
- Final paragraph: here and elsewhere, "The Shapley-Folkman do-dah..." is used far too much as the subject of the sentence. Try turning sentences around by looking for other subjects, and cut down on the tiresome "also"s.
- "The topic of non-convex sets in economics has been studied by many Nobel laureates..."
- I left this to last, as it may be a more substantial issue. This segment of the lead is repeated in the article, but does not really summarize anything. The comprehensiveness criterion really bites here: "it neglects no major facts or details and places the subject in context". The legacy of the Shapley-Folkman Lemma is that results previously confined to convex economics and optimization (relatively easy) could be extended to the non-convex domain (much harder) by averaging (e.g., assuming many agents); this needs to be discussed to place the article in context. The applications section contains some such discussion, but is primarily pedagogical/technical and mixes mathematical, historical and evaluative material. The segment "Starr's 1969 paper and contemporary economics" then ends with a list which cries out for elaboration. Overall the treatment of the economics background, history and legacy for the results falls short of what I would hope for in a featured article. Geometry guy 23:18, 7 October 2011 (UTC)
- Mathematics issues. Considerable effort has been made to explain the mathematics behind the S-F Lemma. This is commendable and appropriate as none of the mathematics is particularly hard (at least in the context of plane geometry), so it ought to be possible to explain it to a wide readership. There are some minor shortcomings in this respect.
- Introductory example. (This should not begin "For example": the section title suffices.) I read this having forgotten the statement of the Shapley-Folkman Lemma and found it didn't help me very much. It isn't clearly laid out as an example of Minkowski addition of two or more sets, and quickly goes on to discuss averages, where I had not yet got the point. There are also little distractions such as describing {0,1,2} as a subset of the integers, which seems irrelevant. At some point, the article should probably introduce the averaged Minkowski sum (and motivate why it is a useful notion).
- Real vector spaces. Is it necessary to use the language of vector spaces if they are all viewed as Rn? Maybe, but readers could easily be put off. Perhaps it is more natural to use vector spaces, but not completely so: the natural setting for convexity is affine geometry, and later on, the theory makes use of Euclidean distance.
- Convex sets... "a non-empty set Q is defined to be convex if, for each pair of its points, every point on the line segment that joins them is a subset of Q". This sentence is incorrect (unless points are viewed as subsets), possibly because of a partial attempt to simplify the exposition. It can be simplified further: "a non-empty set Q is convex if, for each pair of points in Q, every point on the line segment joining them is in Q". In general, it is helpful to unpack the language of subsets, as set membership is easier to discuss in a non-technical way. A small amount of copyediting would be helpful here (and elsewhere).
- Convex sets. "Mathematical induction" disrupts the flow and is only need for one implication in the "if and only if". Why not define convex combinations before using them to characterize convexity?
- Convex hull... "is the minimal convex set that contains Q. Thus Conv(Q) is the intersection of all the convex sets that cover Q." Here the word "cover" is incorrect: its use implies a collection of sets whose union contains Q. Conv(Q) is the intersection of all convex sets containing Q, and the the fancy word "minimal" can be replaced by "smallest" by the uniqueness (well-definedness) of this set. It may be helpful to introduce the word "convexification" here as a synonym.
- Minkowski sum. The "principle of mathematical induction" again. It isn't needed to define the sum of a family, only to show that an iterated binary sum is equal to the sum of the family (and hence is associative).
- Convex hulls and Minkowski sums. Yet more induction! Why is it relevant to discuss a snippet of the proof?
- Statements. This begins in a somewhat pedestrian fashion with "x in Y and Y=Z implies x in Z". Repetition may be pedagogical, but encyclopedic writing should be concise and to the point.
- Statements/lemma. It may be helpful to use a different letter for an element of Conv(Qn) than for an element of Qn. This would help to emphasize the point of writing the sum in two parts.
- Shapley–Folkman theorem and Starr's corollary. There is a sudden jump in complexity and sophistication here. The article has been holding the reader's hand up to the lemma, but then says "okay, now you're on your own". A short subsection on Euclidean distance, distnace to a subset, circumradius and inner radius would help a lot.
- Starr's corollary. Is this really a corollary to the Shapley-Folkman theorem? It provides a sharper estimate. Also, why is "non-convexity" an abuse?
- Proofs and computations. "The original proof of the Shapley–Folkman lemma established only the existence of the representation..." What representation? This needs to be clarified. An idea of the proof of the lemma would be nice too.
- There are a few math issues in the applications section, but I will discuss that separately. Geometry guy 16:27, 8 October 2011 (UTC)
- Further issues. It remains to discuss the Applications section.
- "The Shapley–Folkman lemma enables researchers...and the Shapley–Folkman lemma has renewed research that had been stumped by non-convex sets.'" Why "researchers"? Had "research" really been "stumped"? This informal present/perfect tense approach needs to be backed up or replaced by historical legacy material.
- "In all three disciplines, the break-through application of the Shapley–Folkman lemma has been made by a young scientist." This is an editorial observation; such synthesis should be sourced or cut.
- "On this set of baskets, an indifference curve is defined for each consumer..." suggests there is only one curve per consumer, whereas in fact the space is foliated by such curves: there is one through each basket.
- "An optimal basket of goods occurs where the budget-line supports a consumer's preference set, as shown in the diagram..." There is too much unexplained economics jargon here. What is a budget-line, price vector and endowment vector, and how is the budget line defined in terms of the other quantities? What is an optimal basket? A feasible one? Is the optimal basket really a function? It looks like it could be multi-valued or only partially defined even in the convex case.
- I remain uncomfortable with the griffin example. Apart from the question as to whether it is encyclopedic, it is distracting and confusing. What is meant by half a lion or half an eagle? It only makes sense when discussing dead creatures. Why not have a lion for six months of the year and an eagle for the other six? And surely a contemporary zoo keeper would value a griffin much more highly than a lion or an eagle, because of the fortune to be made out of visiting Harry Potter fans. Finally, the footnote gives a perfectly sensible and completely sourced example (an automobile and a boat) so why not use that?
- "Previous publications on non-convexity and economics were collected in an annotated bibliography by Kenneth Arrow." This is a slightly odd start to a section. Previous to what? Wouldn't it be better to start with Starr?
- "who proved their eponymous lemma and theorem in 'private correspondence' ". No they didn't: they communicated it to Starr in private correspondence or he quoted it thusly.
- The mathematical optimization section spends rather a lot of time defining convex functions. The caption to the diagram is more concise.
- The opening of the probability and measure theory section is confusing. The essence of the discussion is that if random quantity only takes values in Q, then its average, being a convex combination, must belong to the convex hull of Q.
- That completes my review. Geometry guy 17:10, 8 October 2011 (UTC)
- Reply to Geometry Guy
- I have drafted initial replies in my user space. I agree with most of his comments and I concede merit to the others. In general, I would argue that disagreements remain where I am trying to help first-time readers, with less mathematical background, by repetition.
- I acknowledge that GG may well wish that this article was longer and contained more information, but I reply that FA articles need not be perfect; this article contains far more information and has better graphics than any other treatment in world literature. Readers wanting more treatment of e.g. economics should consult the sources given in the article (most of which are missing from even the union of previous articles on this topic), such as Mas-Colell's article on non-convexity and economics (in .pdf format on his home page).
- I thank Geometry Guy again for his careful and conscientious scrutiny. Kiefer.Wolfowitz 10:46, 8 October 2011 (UTC)
- You're welcome. My comments are generally provided "as is" for you and the delegates to make what you will of them. However, I see from your initial response that I need to clarify Leading issues#3 (on the lead sentence). The Shapley-Folkman lemma involves two fundamental ingredients of similar importance: Minkowski addition and convexity. The current lead sentence treats these ingredients differently, referring to Minkowski addition and then defining it, while postponing discussion of the role of convexity. This is not defining. It should not be too difficult to work convexity into the lead sentence, e.g., "In geometry and economics, the Shapley–Folkman lemma describes the extent to which the Minkowski sum of a sets in a vector space is approximately convex." I'm sure you can do better than me, but a good lead paragraph should mention both Minkowski addition and convexity in the first sentence, then define them both. Geometry guy 17:39, 8 October 2011 (UTC)
- Agreed. The muse was not whispering in my ear, but I'm beginning to hear an improved first sentence.
- If you look at my responses in user space (in history), you will notice that I tend to agree with you after first raising some initial (token) resistance.
- I can probably return to this Monday-Tuesday. Kiefer.Wolfowitz 17:59, 8 October 2011 (UTC)
- You're welcome. My comments are generally provided "as is" for you and the delegates to make what you will of them. However, I see from your initial response that I need to clarify Leading issues#3 (on the lead sentence). The Shapley-Folkman lemma involves two fundamental ingredients of similar importance: Minkowski addition and convexity. The current lead sentence treats these ingredients differently, referring to Minkowski addition and then defining it, while postponing discussion of the role of convexity. This is not defining. It should not be too difficult to work convexity into the lead sentence, e.g., "In geometry and economics, the Shapley–Folkman lemma describes the extent to which the Minkowski sum of a sets in a vector space is approximately convex." I'm sure you can do better than me, but a good lead paragraph should mention both Minkowski addition and convexity in the first sentence, then define them both. Geometry guy 17:39, 8 October 2011 (UTC)
- Oppose. Here are some issues with the article as it stands:
- The article never defines "sumset". It begins using the term in the lead, but the non-expert reader may not realize this is meant to be the Minkowski sum.
- In the paragraph where the lead discusses the Shapley–Folkman–Starr theorem, the claim is first made that "[t]heir bound on the distance" does not depend on "the number of summand-sets N, when N > D". It goes on to say that "as the number of summands increases to infinity, the bound decreases to zero". My first thought was that these could not both be true, and that the article was in error. It turns out that I was wrong, because I missed the word "average". I think I won't be the only reader to make this error, so I think the paragraph needs to make a bigger contrast between sumsets and average sumsets.
- Still in the lead: It's not clear to me what a convexified economy is, not even vaguely. Nor is it clear what kind of equilibrium is meant (a Nash equilibrium, I guess?) or how that's different from a quasi-equilibrium.
- In general, the lead spends a lot of time trying to explain the statement of the Shapley–Folkman lemma (and its relatives). That's not the right direction. What the reader needs to learn is, "Why do I care?" Imagine, for example, that I'm a layman who has read a pop economics book, and I know what supply and demand are and what economies are, but I don't know what a convex set or a Minkowski sum is. Why should I learn about the Shapley–Folkman lemma? The lead does not answer this question. The closest it comes is near the end, where it explains that a lot of famous and successful economists have said that the study of non-convex situations is important (the lead has already made it clear that the Shapley–Folkman lemma is important for these). But essentially it's a proof by authority: All these Nobel laureates think it's important, so you should, too! This will not entice a novice reader to continue.
- In general, the article is structured like (I almost hate to say this) a math article. First it describes some preliminary notions (real vector spaces, convex sets, Minkowski sums, etc.). Then it states a theorem. Then it states applications. Kind of like "Definition–Theorem–Proof–Corollary". I realize that we all write this way (including me), but we shouldn't, and we especially shouldn't in an encyclopedia article.
- Right now, the article lacks a history section. I am going to suggest (this is only a suggestion, and there may be better ways of doing this) that you move some of the material from the Economics subsection of the Applications section into a new "History and Motivation" section immediately following the lead. This could put foundational material (like convexity) into a historical context: Before the Shapley–Folkman lemma, economists studied convex economies. Convexity is ..., and these are economies in which ... and they were important because of ..., but non-convex economies, which are ..., were important because ..., and prior to the Shapley–Folkman lemma nothing was known about non-convex economies. If you combine the foundational material with historical context, you make it more interesting and easier to grasp: It comes with vivid examples of what used to be cutting-edge research. By the time you are done with the historical context, you should have managed to introduce the prerequisite material for the Shapley–Folkman lemma. Then you can state it (and its corollaries and variations). Once that's done, you can move on to other applications.
- The optimization section has the same "Definition–Theorem–Proof–Corollary" feel. Again, I think it would be more effective to weave together the history and the prerequisite material.
- I was surprised at how short the section on probabilistic applications is. I don't know how important the Shapley–Folkman lemma is in such work, but you mention that it can be used to prove some analogs of standard results for real-valued random variables (like a law of large numbers and a central limit theorem). It would be good to include some more detail about these so that the reader at least knows how the Shapley–Folkman lemma is relevant (you don't necessarily have to state the theorems to prove this).
- Also, it might be good to explain in more detail how Lyapunov's theorem is related to the Shapley–Folkman lemma.
- Ozob (talk) 02:33, 8 October 2011 (UTC)
Same illustration used twice
File:Shapley–Folkman lemma.svg is used in the article twice. Please choose one location and remove the other, as it is redundant to have it in the article twice. Kaldari (talk) 09:40, 11 November 2012 (UTC)
- The picture has different captions. In the lede, it illustrates the SF lemma. In the early body, it illustrates the convex hull of a Minkowski sum of sets.
- The repeated image is informative each time, and apparently this repetition is accepted by the other readers (many of whom have been reviewers).
- Thanks, 10:06, 11 November 2012 (UTC) — Preceding unsigned comment added by Kiefer.Wolfowitz (talk • contribs)
- Wikipedia articles that use American English
- Wikipedia good articles
- Mathematics good articles
- Old requests for peer review
- Wikipedia Did you know articles that are good articles
- All unassessed articles
- GA-Class mathematics articles
- Mid-priority mathematics articles
- GA-Class Economics articles
- Mid-importance Economics articles
- WikiProject Economics articles
- GA-Class game theory articles
- Mid-importance game theory articles
- GA-Class Systems articles
- Low-importance Systems articles
- Systems articles in operations research
- WikiProject Systems articles
- GA-Class Statistics articles
- Low-importance Statistics articles
- WikiProject Statistics articles







![{\displaystyle [0,1]\,}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/43e2b417e116123c724ee6f69cf309f6ad17a2d0)