Rule 110
| Template:Wikify is deprecated. Please use a more specific cleanup template as listed in the documentation. |
The rule 110 cellular automaton is a one-dimensional two-state cellular automaton with the following rule table:
| current pattern | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
| new state for center cell | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
Rule 110, like the Game of Life, exhibits what Stephen Wolfram calls "Class 4 behavior," which is neither completely random nor completely repetitive. Localized structures appear and interact in various complicated-looking ways. In the course of the development of A New Kind of Science, Wolfram's research assistant Matthew Cook proved that these structures were rich enough to support universal computation. This is an interesting result because Rule 110 is an extremely simple system, simple enough to suggest that naturally occurring physical systems may also be capable of universality—and hence questions about them will often be undecidable. This means they may not be amenable to closed-form mathematical solutions.
Matthew Cook presented his proof before the publication of A New Kind of Science at a Santa Fe Institute conference, which Wolfram Research claimed was a violation of Cook's nondisclosure agreement. The proof was stripped from the proceedings by court order. Nevertheless the proof's existence became known. However, the interest it generated was primarily about the technical details of its construction, rather than the significance of its existence--and hence of a considerably different character from its treatment in the book NKS.
An example run of a rule 110 cellular automaton
The Universality Proof
Rule 110 was shown to be universal (or Turing complete) by showing it was possible to use the rule to emulate another computational model, the cyclic tag system, which is also universal. This was accomplished by first isolating a number of spaceships, self-perpetuating localized patterns, that could be constructed on an infinitely repeating pattern in a Rule 110 universe, and second, devising a way for combinations of these structures to interact in a fashion that could be exploited for computation.
Spaceships in Rule 110
The function of the universal machine in Rule 110 requires an infinite number of localized patterns to be embedded within an infinitely repeating background pattern. The background pattern is fourteen cells wide and repeats itself exactly every seven iterations. The pattern is 00010011011111.
Three localized patterns are of particular importance in the Rule 110 universal machine. They are shown in the image below, surrounded by the repeating background pattern. The leftmost structure, shifts to the right two cells and repeats every three generations. It comprises the sequence 0001110111 surrounded by the background pattern given above, as well as two different evolutions of this sequence.
The center structure shifts left eight cells and repeats every thirty generations. It comprises the sequence 1001111 surrounded by the background pattern given above, as well as twenty-nine different evolutions of this sequence.
The rightmost structure remains stationary and repeats every six generations. It comprises the sequence 111 surrounded by the background pattern given above, as well as five different evolutions of this sequence.
Below is an image showing the first two structures passing through each other without interacting (left), and interacting to form the third structure (right).
There are numerous other spaceships in Rule 110, but they do not feature as prominently in the universality proof.
Constructing the cyclic tag system
Please refer to the images below to help visualize the operation of the machine.
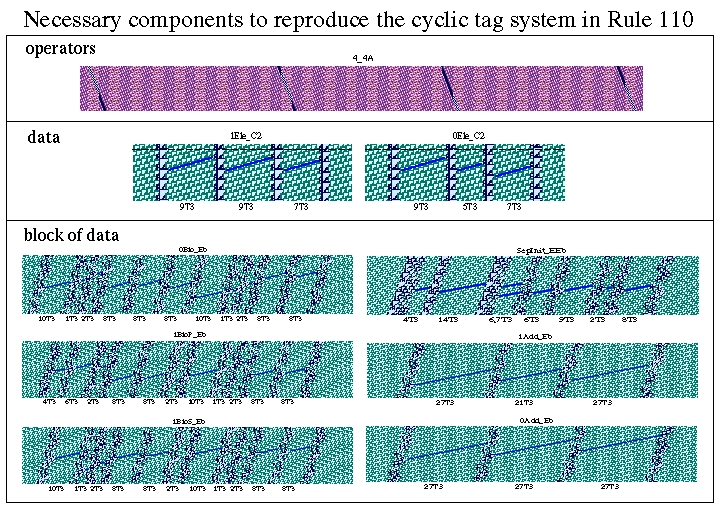
The cyclic tag system machinery has three main components:
- A data string which is stationary;
- An infinitely repeating series of finite production rules which start on the right and move leftward;
- An infinitely repeating series of clock pulses which start on the left and move rightward.
The initial spacing between these components is of utmost importance. In order for the cellular automaton to implement the cyclic tag system, the automaton's initial conditions must be carefully selected so that the various localized structures contained therein interact in a highly ordered way.
The data string in the cyclic tag system is represented by a series of stationary repeating structures of the type shown above. Varying amounts of horizontal space between these structures serve to differentiate 1 symbols from 0 symbols. These symbols represent the word on which the cyclic tag system is operating, and the first such symbol is destroyed upon consideration of every production rule. When this leading symbol is a 1, new symbols are added to the end of the string; when it is 0, no new symbols are added. The mechanism for achieving this is described below.
Entering from the right are a series of left-moving structures of the type shown above, separated by varying amounts of horizontal space. Large numbers of these structures are combined with different spacings to represent 0s and 1s in the cyclic tag system's production rules. Because the tag system's production rules are known at the time of creation of the program, and infinitely repeating, the patterns of 0s and 1s at the initial condition can be represented by an infinitely repeating string. Each production rule is separated from the next by another structure known as a rule separator (or block separator), which moves towards the left at the same rate as the encoding of the production rules.
When a left-moving rule separator encounters a stationary symbol in the cyclic tag system's data string, it causes the first symbol it encounters to be destroyed. However, its subsequent behavior varies depending on whether the symbol encoded by the string was a 0 or a 1. If it was a 0, the rule separator changes into a new structure which blocks the incoming production rule. This new structure is destroyed when it encounters the next rule separator.
If, on the other hand, the symbol in the string was a 1, the rule separator changes into a new structure which admits the incoming production rule. Although the new structure is again destroyed when it encounters the next rule separator, it first allows a series of structures to pass through towards the left. These structures are then made to append themselves to the end of the cyclic tag system's data string. This final transformation is accomplished by means of a series of infinitely repeating, right-moving clock pulses, comprised of the right-moving pattern shown above. The clock pulses transform incoming left-moving 1 symbols from a production rule into stationary 1 symbols of the data string, and incoming 0 symbols from a production rule into stationary 0 symbols of the data string.
Images of the Machine
A stationary symbol meets a left-moving rule separator:

A clock pulse converting a rule into a symbol: File:Ca110-clock.png
Cyclic tag system working
The reconstructions was using a regular language to Rule 110 over an evolution space of 56,240 cells to 57,400 generations. Writing the sequence 1110111 on the tape of cyclic tag system and a leader component at the end with two solitons.
 File:Cts-1.jpg
File:Cts-2.jpg
File:Cts-3.jpg
File:Cts-4.jpg
File:Cts-5.jpg
File:Cts-6.jpg
File:Cts-7.jpg
File:Cts-8.jpg
File:Cts-9.jpg
File:Cts-10.jpg
File:Cts-11.jpg
File:Cts-1.jpg
File:Cts-2.jpg
File:Cts-3.jpg
File:Cts-4.jpg
File:Cts-5.jpg
File:Cts-6.jpg
File:Cts-7.jpg
File:Cts-8.jpg
File:Cts-9.jpg
File:Cts-10.jpg
File:Cts-11.jpg
Differences from a Turing machine
The machine depicted here differs from a Turing machine in two notable ways. First, it has no halting state. When the length of the string in the emulated cyclic tag system goes to zero, the machine ceases to function properly, but the cellular automaton continues indefinitely. Second, the machine requires an infinite repeating pattern as an initial condition. While Turing machines are permitted to use an unlimited amount of tape to perform their computations, all but a finite portion of that tape must be blank at the beginning of the computation.
Formal descriptions of the machine
The function of this machine is briefly described in Wolfram's book, A New Kind of Science.
Since the publication of A New Kind of Science, Matthew Cook has prepared a paper giving the complete proof, now published in Complex Systems, Volume 15, Issue 1 (2004).
References
- Wolfram, Stephen, A New Kind of Science. Wolfram Media, Inc., May 14, 2002. ISBN 1-57955-008-8
- Matthew Cook, "Universality in Elementary Cellular Automata," Complex Systems, Volume 15, Number 1, p. 1-40, 2004.
- Harold V. McIntosh, "Rule 110 Is Universal!," http://delta.cs.cinvestav.mx/~mcintosh/comun/texlet/texlet.pdf, June 30, 2002.
- Turlough Neary and Damien Woods, "P-completeness of cellular automaton Rule 110," Lecture Notes in Computer Science 4051, pp. 132-143, July 2006. (http://citeseer.ist.psu.edu/neary06pcompleteness.html)
- Genaro Juárez Martínez, Harold V. McIntosh, Juan C. Seck Tuoh Mora and Sergio V. Chapa Vergara, "Reproducing the cyclic tag systems developed by Matthew Cook with Rule 110 using the phases fi_1," http://uncomp.uwe.ac.uk/genaro/papers/repCTS_R110.pdf, 2003.
- Genaro Juárez Martínez, Harold V. McIntosh and Juan C. Seck Tuoh Mora, "Gliders in Rule 110," Int. J. of Unconventional Computing 2:1-49, January 2006.
- Harold V. McIntosh, "Rule 110 as it relates to the presence of gliders," http://delta.cs.cinvestav.mx/~mcintosh/comun/RULE110W/rule110.pdf, January 1999.






