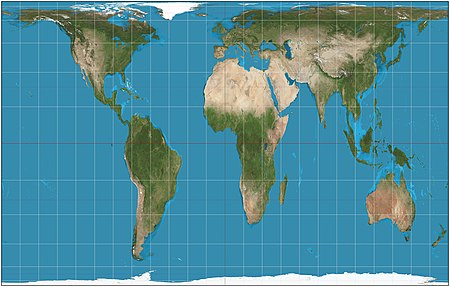
Talk:Gall–Peters projection
| Maps B‑class Mid‑importance | ||||||||||
| ||||||||||
old talk
An example of this one would be great. I'm familiar with the Mercator projection, but can't imagine what this one would look like. --KQ 18:09 Aug 8, 2002 (PDT)
- Here are some samples of various projections (copyrighted page, so we can't steal them): http://www.geog.ouc.bc.ca/physgeog/contents/2a.html --Brion VIBBER
- Here one can find PDF versions of MANY projections: http://www.ilstu.edu/microcam/map_projections/index.html and it says at the bottom "Graphics as of 12/24/2004, created and released into the Public Domain by Paul B. Anderson pbander@yahoo.com (A member of the International Cartographic Association's Commission on Map Projections)" --
- Oh... those. I've seen those. I don't think they'd be too hard to "reverse engineer", actually--just take a PD Mercator projection and use the GIMP or Photoshop to squash it at the top and bottom. I'd try it now except I have to pack for a trip. Anyway, thanks. --KQ 18:19 Aug 8, 2002 (PDT)
- I think (and I might be wrong) that what you've suggest would not work. The Peters map is not just a stretched or squashed version of Mercator. In fact, I think you'll find it's stretched N-S at the equator (but squashed E-W there, relative;y speaking) but at the poles it's the other way around. Anyway, I don't think simple manipulation of a Mercator in GIMP will give you a real Peters, though maybe you could created something that looked a bit like one.
Where can I get data showing the outlines of the continents? With that I could code up the map projections (I have code for some stashed away somewhere, and Gall-Peters is pretty easy) and draw them. -phma
FTA: Within geography more generally, some commentators see the cartographic controversy over the Peters world map as a sign of immaturity in the cartographic profession regarding the fact that all maps are political.
Perhaps I've been drinking the koolaid for too long, but there are technical reasons for some map projects. Or perhaps it is just a coincidence that routes on a Mercator projection are a straight line!
Some commentators may think that all maps are political. I don't doubt that some commentators think that all maps are a conspiracy against flat earthers. :D
I'm unhappy with the wording of the quoted sentence. Perhaps we need a pro/cons section of the article?
--Dasunt 23:26, 5 February 2006 (UTC)
It's impossible to eliminate an "agenda" from a map, since the map has a purpose. All maps distort. You must choose what to put on and what to leave off a map. The agenda, and the decisions that go into fulfilling it, are argued to be "political". While that may be true (depending on definitions), it would be an unfounded leap to claim that the political aspects of most map carry significance for their audience. Therefore I think rather dimly of the unjustified politicization promoted by some commentators, but I don't question the fact that all maps are (at least faintly) political.
Strebe 05:51, 10 April 2006 (UTC)
2021
Yes. No "perhaps" about it. It's astonishing that, in the article about that unprecedentedly-popular map, there's no pros/cons, advantages/disadvantages discussion.
Have we been overzealously editing?
That lack will soon be fixed. -- 22:14, 31 July 2021 97.82.109.213
NPOV
The section entitled "the controversy" needs some serious NPOV work and should have citations. WP doesn't say things like "All of those claims were erroneous", even if such is true, without attributing the statement. – Jonel | Speak 13:12, 8 April 2006 (UTC)
I can't find any citation to justify the claim that Peters finally acknowledged the prior art of Gall. I wonder if he really did.
Strebe 05:40, 10 April 2006 (UTC)
the 'controversy' section says, in part, "Faced with his notoriety, by 1980 many cartographers had turned overtly hostile to the problematic claims many viewed to be truculent, exaggerated, or outright erroneous." wow. there's a serious pov issue here, not to mention a prose so purple it borders on ultraviolet. anyone want to take on a rewrite? frymaster 20:16, 4 May 2006 (UTC)
Frymaster, could you describe precisely what you think is wrong with the point of view, rather than just accusing the prose of having a "serious pov issue"? The passage reports that some cartographers viewed the claims a particular way. That's completely neutral. As for your complaint about the prose color, is it the use of capital letters that blinds you, or was it just the hardly-exotic-words you don't happen to know?
Strebe 23:28, 6 May 2006 (UTC)
- I agree with Jonel and Frymaster that there is a NPOV issue here, the text generally reads as pretty harsh on Peter. Tomgreeny 23:45, 18 February 2007 (UTC)
- Disagree. The entry is as balanced and NPOV as can be expected from a narrow but highly controversial subject such as this one. It would be POV to downplay the controversy, particularly as the PP has been repeatedly and convincingly rubbished (strong though that may sound) in the literature (quite a bit, though by no means a large fraction, of which has been cited in the article).Brockle 10:40, 16 April 2007 (UTC)
Hi, I would like to contribute this NOPV discussion by describing how I ever found this Gall-Peters map: All my life I've seen only two maps; the round globe with a lamp inside (you know, the familiar sphere) and the mercator map in every book I've read. Everytime I saw different kind of map (For example centered on Antarctis) I couldn't relate it to these two maps. I saw the world as a Mercator even though I didn't know its name! I _knew_ that Greenland is not that big but couldn't say how much it was wrong. Then I stumbled on this Gall-Peters kind of map at wall of a hostel. I just couldn't get my eyes from it. Africa was big. Greenland small. It was totally fascinating.
I spent my time searching the map from the internet, and then found this page. It was a total disappointment. I mean, the guy who opened my eyes to the world was seen as an amateur and no-good man in this article. If this is an encyclopedia, I would like to point out that what that man did, made a difference to an ordinary man like me. I don't really care if the map is not mathematically correct or you can't sail with your ship to a another country. I mean.. Now I really understand why Africa countries are so divided. They have a desert as big as Europe!
And finally, my humble proposition to correct this NPOW issue. You could move all the dispute to the Peters' personal page, if that exists. There it wouldn't be such a big NPOW, because if you stumbled _there_ you would like to know the personal battles of that man.
62.142.198.159 10:17, 15 May 2007 (UTC)
- I think that the Controversy section is simply too long and too relevant in this voice. in effect moving it, making a voice apart or make a synthesis would be more effective.
- for example what Peters did or not did in relation with cartography associations should figure under his personal page and if there are a evolution in the consideration of this type of map it should be listed as this, or if there is a "Peters question" in the cartogrphists community it should be listed under its name.
- 80.104.141.45 13.34, 16 May 2007 (UTC)
I don't quite grasp what "too relevant in this voice" means. The Gall-Peters projection is largely defined by the controversy and its history. There probably wouldn't even be a Wikipedia entry for the projection without the controversy. Hence I'm not sure trying to move that section somewhere else would benefit the article. Peters's actions in the affair belong in the discussion of the projection and certainly within the discussion of the controversy. Don't they?
Strebe 01:09, 17 May 2007 (UTC)
- See, I knew the Gall-Peters map also without knowing Peters name and absolutely not knowing this polemics history.
- now it isn't that in this way the voice isn't comprehensible and maybe now I'm more informed on academic diatribes then before, but the voice is about Gall-Peters map that is a quite widely knowed kind of map, different from other Gall projections.
- I'd rahter find relevant an explanation on why the rectangles on the Gall-Peters are not regular squares. wich now I don't know, but I know how this kind of map that I find on my textbooks some year ago have been welcomed 30 years ago.
I'm surprised the NPOV issue seems to be more or less settled when I found the controversy section still quite subjective. Phrases like "crusaders for new projections" and "well-intentioned, zealous, but poorly informed predecessors" in particular slant the article towards a hostile stance against Peters and his arguments in favour of his projection. What about discussing the merits of his arguments more? Wikischolar1983 (talk) 09:57, 23 June 2008 (UTC)
- cru•sade (n.): an organized campaign concerning a political, social, or religious issue, typically motivated by a fervent desire for change.
- It is hard to imagine a more accurate description of the activities surrounding the promotion of the Peters projection. It is also hard to believe Peters or Edwards would not characterize themselves as "crusaders". The word does not carry an innately negative connotation by the dictionary definition or in most people's minds. c.f. "Crusader for peace," or "Crusade against poverty".
- With respect to "zealous" and "poorly informed", did you read the citation that went with it? Do you doubt the cited author? Do you doubt there are such predecessors? Or do you object to juxtaposing them against Peters? Would you prefer "sometimes poorly informed"?
- How does one discuss the merits of an argument that has no verifiable merits? The technical claims are discussed and dealt with. They fare poorly. The single non-technical claim – the psychosocial rationale for the projection – is conveyed under "Peters world map". There is little more that can be said about that claim without speculating, for the simple reason that no one, including Peters, has ever conducted a study that could inform a debate about whether map representation of land sizes would ever influence a person's perception of a country's importance. Meanwhile the only published apologists that I know of are cited – and even they did not endorse Peters's thesis. They merely argued it might have some truth to it or commented on the reactionary cartographic community.
- If there were any peer-reviewed literature supporting Peters's argument, of course it must get cited. There isn't any. The fact that Peters met with considerable successes in promoting his map and its ideology does nothing to change the fact that it's all founded on false claims and a single unverified (and doubtful – c.f. Monmonier) thesis. The usual term for this sort of promotional activity is "quackery", but peer-reviewed commentators have (just barely) fallen short of outright using the word.
- If you object to the tone, then please clean it up.Strebe (talk) 21:07, 23 June 2008 (UTC)
- The problem I have with those phrases is that they inject subjective opinion - no matter how much evidence might be in their favour, they're a subjective description when wikipedia should really be just about the facts. Whether crusade is positive or negative in particular depends on how you view his arguments; if you think that what he said did have merit, then crusade gives the impression that he was hot-headed and had not thought over the substance to his claims, when I think that he most sincerely did. I think there is merit to his argument that Mercator projections were so prevalent because they exaggerated the size of the industrialised, western countries. This might not be verifiable from a strictly cartographic point of view but it still is a valid (ie, reasonable) point to make. The overall tone of the controversy section seems to condemn him for that. Wikischolar1983 (talk) 09:06, 24 June 2008 (UTC)
- You claim that dictionary-accurate phrasing and commentary from cited sources is "subjective opinion". You claim "crusade" connotes "hot-headed", when no dictionary implies any such thing and no one I talk to thinks so – and the point seems particularly weak when the term is not even being applied to Peters. Then you are saying you "think" there are merits to his arguments and that they should be discussed, but with no published material to cite. I do not see how following your recommendations would do anything but change a factual description of the controversy into an opinion piece. The article airs Peters's claims. It is beyond the scope of an encyclopædia to speculate on their merits in a vacuum of literature to cite. Strebe (talk) 22:13, 24 June 2008 (UTC)
- (Sigh) Why do I get the impression I'm dealing with someone who doesn't know what bias is? It doesn't matter what the dictionary definition is, it doesn't matter whether the author of the cited works uses those words or not, the simple fact is the phraseology for an encyclopedia article is too descriptive and subjective and conveys a negative impression against Peters. I don't dispute any of the points raised against PP but in the way it's been worded and that it downplays Peters's own arguments entails a violation of NPOV, particularly when this article is supposed to be on Peters's very projection. Over and out. Wikischolar1983 (talk) 09:46, 26 June 2008 (UTC)
2011
- You can make the controversy clear without using such value-loaded terminology.74.240.51.240 (talk) 07:25, 29 September 2011 (UTC)
- The Peter's projection isn't mathematically incorrect.74.240.51.240 (talk) 07:27, 29 September 2011 (UTC)
- No map projection is absolutely "incorrect", as long as it's self-consistent and well-defined. Nevertheless, the Gall-Peters projection has features (such as shape distortion) which seriously compromise its usefulness in its main intended uses. The only true advantage is that it's equal-area, but there are plenty of other equal-area projections to choose from... AnonMoos (talk) 19:59, 29 September 2011 (UTC)
- Precisely. This projection is no more and no less than any other cylindrical projection: unfit for representing the world due to the extreme shape distortions. I still wonder how its proposal got so much attention! Alvesgaspar (talk) 22:46, 29 September 2011 (UTC)
- No map projection is absolutely "incorrect", as long as it's self-consistent and well-defined. Nevertheless, the Gall-Peters projection has features (such as shape distortion) which seriously compromise its usefulness in its main intended uses. The only true advantage is that it's equal-area, but there are plenty of other equal-area projections to choose from... AnonMoos (talk) 19:59, 29 September 2011 (UTC)
- Yep, me too. I don't have an opinion on the Gall-Peters projection and its relative merits and drawbacks compared to the Mercator; I was drawn to the comments section because the article seemed unusually hostile towards the GP projection and used several sweeping phrases to characterise response that seemed, at the least, a bit rich. "The cartographic community met Peters's 1973 press conference with amusement and mild exasperation" is not an NPOV phrase. "In the ensuing years, however, it became clear that Peters and his map were no flash in the pan" is not an NPOV phrase. "The 1980s saw a flurry of literature directed against the Peters phenomenon. Though Peters's map was not singled out,..." - so who exactly decided that the "flurry" was directed against Peters specifically? Wikipedia is meant to be a repository for fact, not a vehicle for contributors to exercise nascent storytelling skills; unsupported (indeed, unsupportable) rhetoric has no place in the article. 220.239.203.208 (talk) 01:41, 14 December 2011 (UTC)
- Peters was motivated by the best of intentions, but he seems to have been completely cut off from any real knowledge of mainstream modern cartography, or direct personal contact with professional cartographers or geographers, until after he had already launched into his public PR campaign. Sometimes such isolation can be a good thing (allowing for fresh perspectives, see Ramanujan in mathematics), but in this case it was mostly a bad thing -- since Peters almost literally reinvented the wheel (inadvertently independently rediscovering an 1855 map projection), and he seems to have had some kind of idea that Mercator was the stifling unquestioned orthodoxy among geographers, when in reality many professional geographers hated Mercator just as much as he did. And his map projection just wasn't very good -- it was certainly equal-area, but there are a lot of equal-area projections around, and a number of them have fewer disadvantages than Gall-Peters. The discrepancy between these factual realities and Peters' grandiose claims and sweeping rhetoric generated widespread negative opinions in some circles, and we can report on such opinions in the Wikipedia article (as long as they're sourced, relevant, etc.)... AnonMoos (talk) 04:32, 14 December 2011 (UTC)
Citation needed ?
The paragraph about the names given to the Gall-Peters projection is crisp clear and absolutely neutral. In its last period it is said that, in recent years, the designation Gall-Peters “seems to prevail” . Why is a citation needed to justify this statement? Is there any published study revealing a systematic counting of all written and spoken occurrences? If not, better to accept the fact that, in specialized literature, the name Gall-Peters is indeed prevailing. Of course, I took off the “citation needed” tag. Alvesgaspar 08:31, 12 May 2006 (UTC)
Given that Peters is a highly controversial subject and the camps for and against it highly polarised, I agree that the tenor of this article is well balanced, fair in how it represents both sides of the arguments, and as much NPOV as possible. Peters has been roundly criticized, not only by stodgy cartographers, as some of Peters's defenders would have it, but by a broad range of geographers, including many with interests or involvement in the sorts of broad social and development issues and movements alluded to in the article. Brockle 10:31, 16 April 2007 (UTC)
Individual points needed
It would be nice to have a list of the individual points the map aims to address. That is, the fact that the equator is placed in the middle, the Greenland v.s. Africa problem, North v.s. South , europe v.s. Africa and so on. Those are found on the web site and on the actual printed maps as well.
- That would be fine, but not in a vacuum of cited analysis. Those points were all red herrings. Strebe (talk) 22:24, 24 June 2008 (UTC)
Explicit formula?
Could someone please add the function that relates a point of the Earth's surface to the point on the map under hits projection? Tompw 16:43, 20 June 2006 (UTC)
- Here it is: x = cos(45)*long; y = sin(lat)/cos(45) (lat = latitude, long = longitude) Alvesgaspar 21:45, 20 June 2006 (UTC)
- Looks about right, I TeXified that and put it in; also included the alternate form of cos(45) for the sake of it, it's a bit nicer-looking I think. --tiny plastic Grey Knight ⊖ 11:25, 13 February 2008 (UTC)
Perhaps this is nit-picking, but I think the formula mixes radians and degrees. As it stands, using degrees, the map would be 180 sqrt(2) units wide and 2 sqrt(2) units tall, an aspect ration of 90:1 rather than the (pi/2):1 it really is. Is it easier to clarify that the lat and long are in radians or to convert the 45s to pi/4s? 81.129.214.254 (talk) 13:30, 28 June 2008 (UTC) Kensson
New image
I've replaced the old line drawing with a projection of a satellite view of the Earth. The black bars on each side may be "disturbing", but it needs to be noted that this is part of a larger series of images of projections I have prepared with a common image size to ease comparisons. For example, view this article in one window and you can "blink" compare with Winkel Tripel or Goode homolosine projection and so forth in another window. Of course, if this is insufficient rationale, feel free to revert and I'll leave this article all by itself. mdf 14:40, 14 September 2006 (UTC)
Confused
"the surface area of a sphere and area of the cylinder containing it are equal." --area is a 2D concept and a cylinder is a 3D figure, I truly don't understand what this could possibly mean (& "containing it" is a very vague term)
I'm confused by your confusion. Earth's surface is a 3D object. Are you saying you don't see how the Earth's surface could have area, either? A cylinder has a surface. Any surface has area. The exterior surface of the minimal open cylinder containing a sphere has the same surface area as the sphere it contains. The text expresses the notion correctly and concisely, albeit not pedantically completely. Strebe 23:21, 20 April 2007 (UTC)
no the text says "surface area" of a sphere and "area" of a cylinder, it should say "surface area" of a cylinder but it should also define "containing it" such that the two surfaces are tangent at however many points but do not otherwise intersect, I'll fix this just felt bizarre doing it when i have no idea of the truth of the statement
... & don't patronize me 140.247.47.139 03:37, 23 April 2007 (UTC)
This is ridiculous
There is scarcely any connection between the land area of any given state and its population, political system, economy, and foreign relations. How exactly is this projection a "social justice" issue?
- Really? As far as population, 3 of the 5 largest countries in the world by size are the largest in terms of population. 3 of the five smallest by area are the smallest by population. I would guess that monarchies are more likely to occur in your Monaco's and Lichtenstein's than in your Russia's and China's. Economy? I'd far sooner face an embargo from San Marino than I would with Brazil. And if you don't think the big, populous countries don't have more weight to throw around in foreign policy, you're kidding yourself. It sure seems like a "social justice" issue to me.--YbborTalk 00:18, 1 October 2007 (UTC)
- Yes, really. You chose 3 of the 5 largest countries when the two largest don't suit your argument at all. There is some correlation between land area and population for the simple reason that a bigger country can hold more people. The correlation is weak, though; so weak that the largest by area doesn't even make the top 5 in population – and you're the one who arbitrarily chose "top 5" to make your point. The second-largest hardly ranks at all. What sense does it make to demand an equal-area map to represent PEOPLE when the correlation is so low? You go on about correlations with political systems and economies, but again neither of those correlations is perfect or even strong. You're the one kidding yourself with sophistry. A perfectly equal-area map is no better than a compromise projection for "social justice" because the association between population and land area is so weak. And in any case, there are, and always have been, an unlimited number of equal-area maps to choose from.
- The only reason this projection is a social issue is because a small group of loud people have adopted it as their symbol. It has nothing to do with the objective merits of the projection. Strebe 20:05, 1 October 2007 (UTC)
- Absolutely not ridiculous. In the typical Mercator projection tropical cuntries are very reduced in size in comparison with sub-artic ones. Europe seems doubly large than it is while Africa or India look terribly smaller than they actually are. It's not a matter of population (that may evolve) but of real areas.
- Even in a map of Europe for instance, Spain looks smaller than Sweden, when it's a lot larger. Or, again in the global map, Australia looks smaller than Greenland. That's the problem with Mercator projection or raher with the widespread use of this (otherwise useful) projection in nearly every sort of maps.
- Peters projection solves this quite well.
- The problem is that some "loud people" prefer to see Greenland several times its size strenagely enough. But, well, Wikipedia is not a forum. Let's stay focused. --Sugaar (talk) 03:29, 5 December 2007 (UTC)
- What does Mercator have to do with anything? Everybody already agrees: we should not use the Mercator projection for general reference world maps. It's not about Mercator. It's about Peters. Perhaps YOU should stay focused. Strebe (talk) 17:33, 5 December 2007 (UTC)
Gall-Peters? Aren't both "projections" different?
According to this site (admitedly apologetic of Peters' work and ideas, but also showing clear knowledge of the issue) Peters' "construction" (sic) is not Gall's projection, even if they may have some similarities in aim.
In quotes:
The difference between the Gall's Ortographic Projection and Peters-Map is:
- Rev. James Gall assumes the earth as a sphere and projects his grid trigonometrically with the standard-parallel of 45°.
- For his construction Arno Peters assumes the earth as an ellipsoid and he develops his grid geometrically on the basis of area computations. The latitude of no distortion (standard-parallel) results from the method of construction and varies with the selected ellipsoid.
The world maps of Arno Peters and Rev. James Gall are very similar but they are not identical. A Peters-Map can only be such which has been designed using his method of construction. Any other map which has not been designed using Arno Peters method of construction can never be a Peters-Map.
There is more: the Peters method (not any simple projection but rather a construction) in whole detail, etc. While the results may be apparently similar, Peters' product seems to be a true equal area map, while Gall's is only an approximation.
I'd suggest that the cartographers around take an in-depth look and proceed to split (and clean up) the article accordingly. --Sugaar (talk) 03:20, 5 December 2007 (UTC)
- You seem to assume, because the article you cite describes both the ellipsoid and the Peters projection, that Peters must have based his maps on ellipsoids. He didn't. His own written description of his method do not discuss development on the ellipsoid; nor is there any reason to because the difference between the spherical Gall-Peters and the ellipsoidal Gall-Peters is negligible. Gall's projection is perfectly equal-area. It is also a "construction", like almost all projections in actual use.
- These distinctions you strain to find between the Peters projection and the Gall are no distinctions at all – and even if they were distinctions, the distinctions would have no meaning because they would be imperceptible. You are reading far, far more into the science of Peters's projection than Peters himself put into it. He was all about the big struggle, not struggles so tiny that you have to argue whether they even exist. I think he'd be embarrassed to have someone defending the uniqueness of his projection by resorting to splitting microscopic hairs. Strebe (talk) 18:02, 5 December 2007 (UTC)
- Well, it does seem they are different methods. I know Peters never made an issue of it but in any case, it does seem that the people defending they are one, are ignorant of Peter's system.
- Additionally there are several Gall projections, the one similar to Peters' being (if I'm not wrong) the stenographic one. --Sugaar (talk) 00:02, 7 December 2007 (UTC)
- No, the Peters projection is the same as the Gall orthographic – read the Wikipedia article, at the very least. There is no "Gall stenographic"; there's a "Gall stereographic". There is no controversy over whether the Peters projection is the same as the Gall orthographic. It is the same. There are people who have actually studied this stuff, if you can imagine, and they are well cited in the Wikipedia entry. One of them (Snyder) was the dominant map projections expert of the 20th century. This is not a productive conversation. Strebe (talk) 20:26, 7 December 2007 (UTC)
- Nice to meet you here, daan! Still struggling with the Peters projection? Maybe a new religion will be created soon; and then, it will be a matter of faith and no rational arguments will be allowed any more! Regards, Alvesgaspar (talk) 00:18, 8 December 2007 (UTC)
My, there seems to be plenty of heated discussion on this page - I had no idea the Peters projection was so controversial. What an interesting read! I agree that given the strong feelings displayed above, the controversy section is neither too long, nor misplaced in this article. I also feel that it could be reworded to clarify who thinks what and why. Right now it reads a bit like a specialist's argument with other specialists - so to a relative novice on the subject, it's confusing. For example, in this phrase: "Mercator's inappropriate use in world maps..." Marcato's inappropriate use of what? And why is it inappropriate? Or rather, who thinks so - Peters himself? Maybe the experts or the original author could help us out on these things. Ah, and on that note: I don't understand the relevance of the middle paragraph in the "Peters World Map" section; why does it matter if there was a discrepancy between his text and the description? [Does 'description' here mean 'image'?] Obviously it must be important to somebody, or it wouldn't be included, but from the lay-perspective it's quite confusing. Please help? Thanks! Isocephaly (talk) 00:35, 4 January 2008 (UTC)
- Thanks for the comments. I agree that some of the verbiage could be simplified. You have changed the meaning in some places, so I hacked at it a bit more. Take a look at the revisions to see if you think it's improved. Strebe (talk) 20:26, 4 January 2008 (UTC)
is it Peters' or Peters's?
The Wiki article on use of an added 's' after a possessive apostrophe indicates that it should be dropped where the 's' sound makes including it difficult to sound. Now is Peters' easier to sound that Peters's? I think it is. But whoever wrote the article has committed the 'sin' of repeating Peters's so many times that I have only amended it where it first appears - and I would leave to the consensus view to decide whether to change this throughout. But to me it looks and sounds all wrong. —Preceding unsigned —Preceding unsigned comment added by 172.141.230.187 (talk) 15:29, 19 January 2008 (UTC)
- And to me it looks all wrong not to add the apostrophe "s". All of the journals I have written or reviewed papers for require the added "s". The Wikipedia style guide mostly wants consistency throughout the article. I will note, however, the style guide's comment: "Most respected sources require that practically all singular nouns, including those ending with a sibilant sound, have possessive forms with an extra s after the apostrophe. Examples include the Modern Language Association, The Elements of Style, and The Economist. Such sources would demand possessive singulars like these: Senator Jones's umbrella; Mephistopheles's cat." A very few exceptions are generally agreed upon, and Peters is not one of them. Strebe (talk) 23:19, 19 January 2008 (UTC)
- I will also note there is no audible way to distinguish between Peter's (the name is Peter, and he's got something) and Peters' (the name is Peters and he's got something) if you do not pronounce the second as Petersez. The English possessive comes from the archaic usage "noun + his", as in, We ogled Peters his map a long while. Contracted, that is pronounced Petersez, not Peters. Hence there is no historical justification for eliminated the added "s", either spoken or written. Strebe (talk) 23:25, 19 January 2008 (UTC)
- That's not historically correct -- see English possessive#History... AnonMoos (talk) 15:39, 29 April 2014 (UTC)
- Interesting. Apparently I've read too much Elizabethan literature. The usage was in fashion then. Strebe (talk) 19:23, 29 April 2014 (UTC)
The Real Deal
From Bob Abramms, Peters Map publisher for North America: "I interviewed Dr. Arno Peters on videotape for over 25 hours during October of 2001. I can clarify some of the misconceptions that abound in the above exchanges. (1) Peters did acknowledge the existence of the Gall projection, but he only discovered it some time after the cartographic community took him to task for allegedly plagiarizing Gall's work. Gall's work was mathematical in nature as are nearly all map projections. (2) Peters initial work to create his projection was a cumbersome, laborious hand-drawing of the world, taking each quadrant of the graticule and stretching and squeezing the landmasses to fit a rectilinear map. (3) Only after his projection generated intense controversy with his exaggerated claims, did he turn the cartographic duties over to Terry Hardaker at Oxford Cartographers in Oxford UK. (4) Oxford Cartographers then took Peters “construction” and transformed it into a map based upon mathematical formulae. I argued with Arno Peters at length attempting to get to him modify some of the exaggerated claims printed on the right side of his wall map. It was to no avail. When I discussed this with Terry Hardaker at Oxford Cartographers, even Hardaker admitted he didn’t fully understand or agree with Peters claims. But Peters was a bit stubborn, and he refused to modify the map surround text to accommodate either Hardaker or myself. I recognized from a very early point that Peters’ overblown assertions were hurting the credibility of the map. Only after Arno Peters death was I able to revise the map text to make it more accurate. I believe it currently is cartographically accurate and entirely defensible. My documentary film, based on the Peters interviews in Bremen Germany, is now complete (Arno Peters: Radical Map, Remarkable Man). Bob Abramms www.ODTmaps.com 413-549-1293
˜˜˜˜Denis Wood
Denis, now that ODT's DVD is published I added a citation. But I don't see that the DVD narrative contradicts the Wikipedia text as it stands or demonstrates any "misconceptions" or even adds anything relevant. Of course you or Bob Abramms or anyone else is free to edit as you see fit. Strebe (talk) 05:53, 11 June 2008 (UTC)
It seems Peters rediscovered the cyclindrical equal area map and the notion of standard parallels. The standard parallels make it eurocentric (ironically) but they also make it a viable map. The standard cylindrical equal area turns Europe into a roadkill. I don't see why anyone should try to insist that cylindrical maps should not be used for the world. Sure it has bad distortion but that is unformly oriented- unlike Mollweide-type that bend continents in a funny way-usually Australia suffers worst.
Jay Jackson
POV issues in Controversy section
The 'controversy' section of this article, as discussed above, has some POV issues. It does not read like a neutral assessment of the debate, but rather a criticism of the Gall-Peters projection from someone opposed to it. I've edited it in an attempt to remove the non-neutral language; explanations of my removals are below:
- 'Crusaders' > 'Campaigns' - while perhaps accurate in this case, I don't think it's neutral to describe a political campaign as a 'crusade'.
- Removed '... for the simple fact that it lacked any remarkable properties. Peters's co-option of it did nothing to change that.' The fact that we discuss this map in such detail here suggests that it does have 'remarkable properties'; at least, some people thought it did, which is why there was such an effort to promote it in the 1970s. The amount of attention the projection has received makes it remarkable, if nothing else does. (Also, 'co-option' implies Peters 'borrowed' an existing projection rather than coming up with it himself.)
- 'eerily similar' > 'similar' - arguably an insertion of POV.
- 'any other of the long line of (perhaps) well-intentioned, zealous, but poorly informed predecessors' > 'any of his predecessors' - the inserted 'perhaps' here is a weak attempt to make this description more neutral. Not everyone who has proposed a new map projection in the past was 'zealous' and 'poorly informed' and it is POV to argue otherwise.
- Removed entirely: 'Indeed, most ironically, the only region lacking distortion happens to be along a latitude just south of Arno Peters's native Germany[1] (and the opposite latitude in the southern hemisphere), not anywhere in the technologically underdeveloped world.' 'Ironically' is one of the words editors are specifically advised to avoid in Wikipedia articles, because its application is almost always disputed. This particular observation adds nothing to the article, and reads like an attempt to mock Peters and his political agenda.
The rest is basically acceptable, and I'll leave it for now. If you disagree with any of these edits, please discuss them below rather than just reverting. Terraxos (talk) 05:19, 15 July 2008 (UTC)
- I disagree that the rest is basically acceptable. It still reads like an attack against Gall-Peters rather than a description of the controversy itself. I don't really contribute to Wikipedia at all and yet, reading this I felt compelled to make a comment here. It's pretty bad. 60.242.32.137 (talk) 07:44, 28 March 2013 (UTC)
- Well, it's objective that Peters didn't bother to consult with any professional geographers and cartographers before launching his publicity blitz -- and therefore reinvented an 1855 map projection without understanding that that's what he was doing, and held a completely untrue and blatantly factually false misimpression that professional geographers and cartographers supposedly loved Mercator. And it's fairly objective that Peters gave forth with a lot of grandiose bombastic pompous rhetoric about how his projection was the greatest thing since sliced bread, but very few of these claims (other than the projection being equal area) held up and/or were relevant to choosing which map projection to use. Peters seems to have had very good intentions in some respects, but his belief that no-one before him had ever thought as deeply as he did about the social implications of map projections, and his unwillingness to listen to people who knew a lot more than he did about certain technical issues, meant that he stirred up a lot of antagonism which hindered his stated goals. AnonMoos (talk) 16:14, 28 March 2013 (UTC)
- If presenting the facts as documented by the sources amounts to an attack, then there is no way to fix the article. We can deal with any specific problems someone wants to moot. Strebe (talk) 21:09, 28 March 2013 (UTC)
the entire class of equal-area cylindric projections
I see that Gall–Peters_projection#Discussion lists a bunch of slightly different equal-area cylindric maps.
My understanding is that this entire class of maps -- the entire class of equal-area cylindric projections -- has been named Lambert cylindrical equal-area projections.[1] Each map in that class has a width/height ratio of where is the particular standard of latitude picked for this map.
In particular, the Gall-Peters projection is a special case of the Lambert cylindrical equal-area projection with a standard latitude of 45°.
Is there a more specific name for the special case of the Lambert cylindrical equal-area projection with a standard latitude of 0°?
Is there any reason not to move most of the general discussion of this class of maps out of this Gall–Peters projection article and into the Lambert cylindrical equal-area projection article? --68.0.124.33 (talk) 07:59, 13 July 2010 (UTC)
- The map projections literature nomenclature generally assigns "Lambert cylindrical equal-area projection" only to the case where the standard parallel is the equator. The more general name is "cylindrical equal-area". The redirect from "Cylindrical equal-area projection" to "Lambert cylindrical equal-area projection" is not good and needs to get fixed.
- This article discusses how the projection is constructed and its relationship with other projections so that the reader can reach "his" own conclusions on how significant a development the projection is and can grasp the arguments in play in the controversy. There is no reason the information could or should not be repeated in the article on the cylindric equal-area projection, but I do not think the fact that it appears there argues that it should not appear here as well. Strebe (talk) 19:39, 13 July 2010 (UTC)
- I agree that cylindrical equal-area projection should link to an article that discusses the general mathematics that apply to all cylindrical equal-area projections to that article.
- The current version of the Lambert cylindrical equal-area projection article leads me to think that "Lambert cylindrical equal-area" is a synonym for the entire class of "cylindrical equal-area projection". Can we improve that article so that people like me understand that Lambert is the specific "standard parallel is the equator" case?
- I'm a bit confused -- you mention "the article on the cylindric equal-area projection", but as far as I can tell that article does not yet exist.
- Are you referring to the "cylindrical" section of map_projections#Cylindrical or list_of_map_projections#Cylindrical?
- Or are you suggesting that Wikipedia ought to have an entire article that covers all the cylindrical equal-area projections?
- That other article would be analogous to Weisstein's Cylindrical Equal-Area Projection article.
- Should we create that article by WP:SPLIT this Gall–Peters projection article into two articles -- an article that covers the general mathematics that apply to all cylindrical equal-area projections, and this Gall–Peters projection article that covers Mr. Peters and the history of his specific map, repeating some of the information from that other article? --68.0.124.33 (talk) 19:27, 14 July 2010 (UTC)
- "Cylindric equal-area projection" = "Cylindrical equal-area projection", which presently redirects to Lambert cylindrical equal-area projection. "Cylindrical equal-area projection" and "Lambert cylindrical equal-area projection" articles ought to get split into two. The former should contain information common to all cylindric equal-area projections, including listing the specializations. Lambert is a specialization. It needs only information specific to the specialization.
- I do not favor removing the Gall-Peters projection#Description section from Gall-Peters. The information in its Discussion section should be repeated in the cylindric equal-area projection article, but the latter ought to provide much more information about the entire family of projections. Strebe (talk) 01:18, 15 July 2010 (UTC)
 Done. As you suggested, I built up the cylindrical equal-area projection article (formerly a mere redirect) by copy-and-paste from a few Wikipedia articles (see article history for details).
Done. As you suggested, I built up the cylindrical equal-area projection article (formerly a mere redirect) by copy-and-paste from a few Wikipedia articles (see article history for details).- I thought it would be easier to copy big chunks from those articles and then edit it down, rather than build it up a line at a time.
- Like all Wikipedia articles, I hope later editors will continue to edit and improve it. --DavidCary (talk) 19:38, 15 July 2010 (UTC)
Map artwork
I agree a new illustration is needed. The processed satellite imagery used in many of the map projection illustrations throughout Wikipedia are not suitable because the dark color of the terrain obscures anything else that might be needed on the map. Hopefully we can move to something similar to what is on the Transverse Mercator page, for example, although a good deal of discussion should precede any such move. The image User:Tjic has twice inserted is unusable, however.
- The text is an illegible mess strewn about the map.
- The stated rationale for using it, “changed from a photo image to an actual map, for consistency with other pages about projections”, is wrong because no other map projection page uses maps with illegible text.
- The stated rationale is wrong because most projection pages do, in fact, use processed satellite imagery: c.f.
- Aitoff projection
- Azimuthal equidistant projection
- Bonne projection
- Craig retroazimuthal projection
- Cylindrical equal-area projection (which is the generalized Gall-Peters).
- Dymaxion map
- Equirectangular projection
- Goode homolosine projection
- Hammer projection
- Kavrayskiy VII projection
- Lambert azimuthal equal-area projection
- Lambert cylindrical equal-area projection
- Mercator projection
- Miller cylindrical projection
- Mollweide projection
- Peirce quincuncial projection
- Polyconic projection
- Robinson projection
- Sinusoidal projection
- Two-point equidistant projection
- Van der Grinten projection
- Wagner VI projection
- Werner projection
- Winkel tripel projection
I only found two projection pages that use political boundaries.
Neither of them had illegible text, or any text at all. There is good reason to put both a physiographic map and political map on a page, but not one with illegible elements. Illegible elements are confusing, visually disruptive, not informative, not cartographic, not æsthetic, not professional, and not precedented. Strebe (talk) 19:34, 14 October 2010 (UTC)
Replace low-contrast images
I will be replacing images on the various map projection pages. Presently many are on a satellite composite image from NASA that, while realistic, poorly demonstrates the projections because of dark color and low contrast. I have created a stylization of the same data with much brighter water areas and a light graticule to contrast. See the thumbnail of the example from another article. Some images on some pages are acceptable but differ stylistically from most articles; I will replace these also.
The images will be high resolution and antialiased, with 15° graticules for world projections, red, translucent equator, red tropics, and blue polar circles.
Please discuss agreement or objections over here (not this page). I intend to start these replacements on 13 August. Thank you. Strebe (talk) 22:39, 6 August 2011 (UTC)
Circles -vs- Spheres
"Maps based on the projection continue to see use in some circles." -- shouldn't that be "in some spheres"? Xardox (talk) 01:48, 17 August 2013 (UTC)
- Cute… but confusing. :-p Strebe (talk) 20:54, 17 August 2013 (UTC)
West Wing details
(Moved from User:Strebe's talk page.) I would argue that a 180-degree rotation is quite a relevant difference. Furthermore, the article opens the door to explaining the reasoning behind the use of that specific map by stating that "prominence to countries in less technologically developed parts of the world that are otherwise underestimated". Finally, while I understand that you strive for editorial cohesion, the strength of Wikipedia lies in the non-linear connections made between various articles, rather than being just a straight forward encyclopedia. — Preceding unsigned comment added by 82.217.20.146 (talk) 20:56, 6 January 2014 (UTC)
- I have reverted your edit again. No scholarly articles bother to mention the West Wing appearance; the entire West Wing paragraph is already unsourced trivia constituting WP:OR and lacking WP:NOTABLE credentials. It’s also too detailed already even allowing for a little trivia. The fact that the map is south-up is not important to the article in any sense: regardless of any spherical coordinate rotation, the map projection is the same. I don’t follow your other justifications. Meanwhile “affective associations between vertical position and valence of traditional maps” sounds like buzzword babble and an over-the-top attempt at intellectualism, which fails in this article since it is unexplained and means nothing to anyone who hasn’t read Meiers et al, who made it up. Claims like this have to be sourced—but but in some other article where they are relevant. Strebe (talk) 07:58, 7 January 2014 (UTC)
- If the map's South-at-top nature is as important as its Gall-Peters nature in trying to shake up things that are commonly taken for granted, then I don't see any harm in mentioning it (though not discussing it at any length)... AnonMoos (talk) 18:45, 7 January 2014 (UTC)
- Again, mentioning the West Wing appearance at all is dubious, as is the whole “In popular culture” section, since nothing in it is sourced. I have restored mention of south-up, but I reiterate its irrelevance. The article is about the Gall–Peters projection, not about shaking up things that are taken for granted. Strebe (talk) 19:02, 7 January 2014 (UTC)
Irony
The word "irony" should almost always be avoided because it is so often misused, as it is in this article. In the 'Controversy' section it states that "Several scholars have remarked on the irony of the projection's undistorted presentation of the mid latitudes, including Peters's native Germany, at the expense of the low latitudes, which host more of the technologically underdeveloped nations". That is not ironic so the word "irony" should be removed.
Ciao for now! FillsHerTease (talk) 08:52, 20 April 2014 (UTC)
- It’s not helpful to proclaim something is wrong without explaining why. On the face of it, that is a correct use of “irony”. New Oxford American Dictionary: “A state of affairs or an event that seems deliberately contrary to what one expects.” Strebe (talk) 11:02, 20 April 2014 (UTC)
- Hi. Sorry for the delayed response AND for not explaining why it isn't irony. In the first place you have pretty much covered it yourself with your definition from the New Oxford American Dictionary. There is nothing "deliberately contrary to what one expects" in a distorted two dimensional map projection. All two dimensional map projections are distorted in one way or another. The reason it is being referred to as ironic is that this particular projection makes Peters' native country appear larger than others. That simply isn't ironic, it's just a coincidence. The best example of irony I have ever heard is that when there was an assassination attempt of Ronald Reagan, none of the bullets which were fired hit him directly. However the car he was about to get into was bullet-proof and as a result one of the bullets ricocheted - which wouldn't have happened if the car WASN'T bullet-proof - and hit him. That is ironic! In that song 'Ironic' by Alanis Morissette, none of the examples she sings about are actual examples of irony. The fact that a song entitled 'Ironic' attempts to give examples of irony but fails to do so does in fact make the song ironic after all. Now THAT'S ironic! One of the examples she gives is an old man who wins the lottery but dies the next day. That is not ironic, it is just a terrible coincidence. Much the same way as the map projection distorting Peters' home country is a coincidence, not irony. If an old man played the same lottery numbers every week for 50 years, then finally gave up because he decided he was never going to win, then his numbers came up the next time around, then THAT would be ironic. Does that all make sense?FillsHerTease (talk) 02:32, 24 July 2014 (UTC)
- The reason it is being referred to as ironic is that this particular projection makes Peters' native country appear larger than others. No, it’s an equal-area map, so everything is precisely the correct size, and there isn’t any particular illusion in play to make it seem larger. Unlike most of the world, Germany is correctly shaped. Given that Peters’s intent was to eliminate the “favoritism” he saw in the the Mercator representation of Europe and North America, the fact that his map represents those areas more favorably than the regions he purported to “empower” illustrates the very definition of irony. I don’t care to speculate on whether the effect of Peters’s choice is coincidence or deliberate, and if deliberate, why he did it. Those considerations are irrelevant to irony, the definition of which I will not debate any further beyond suggesting that the constraints you put on the definition are not generally accepted. The complete definition (#3) from Oxford English Dictionary says, “A state of affairs or an event that seems deliberately contrary to what was or might be expected; an outcome cruelly, humorously, or strangely at odds with assumptions or expectations.” Strebe (talk) 06:48, 24 July 2014 (UTC)
- There are many definitions of irony available, including one on Wikipedia itself, which clearly show that the definition used in the article is incorrect. What you would call ironic, but which isn't, is the fact that the very definition you provide yourself flies in the face of your own statement. The word 'deliberate' appears in the definition and yet you completely ignore it, immediately after stating that you "...don’t care to speculate on whether the effect of Peters’s choice is coincidence or deliberate, and if deliberate, why he did it. Those considerations are irrelevant to irony...". I obviously have no hope against that level of determination so I give up! :-) FillsHerTease (talk) 11:34, 31 August 2014 (UTC)
- No, sorry; the article on Irony defines the word in the lede, and that definition matches the usage in this article. But that’s irrelevant. You could simply have registered your dissent by saying you disagree with the word “irony” encompassing situational irony, and I would have said English has long since expanded beyond the word’s etymology, and the conversation would have been over unless you had tendered some better proposal—but of course you cannot, which is why the meaning of the word “irony” has expanded over the centuries. In particular it is disingenuous to keep calling “incorrect” that which is accept by modern usage, by any modern dictionary, and by the blessings of many modern scholars. Strebe (talk) 20:25, 31 August 2014 (UTC)
- Well ... as I said I obviously have no hope arguing against a level of determination which keeps referring to definitions which prove me right but then claims the opposite. Once again, you would call that 'irony' but it isn't. The lede in the 'irony' article very obviously shows that the usage in this article is wrong. Exactly the same as the one from the Oxford English Dictionary that you provided. There is no definition of irony which fits the article and there are no modern scholars who would agree that it does so, no, I'm not being disingenuous at all. What is happening here is that you are defining irony to mean coincidence, just as many people do (e.g. Alanis Morissette, as described above). The fact that many people don't understand the correct usage does not mean the definition has changed and the incorrect usage does not have the blessing of any modern scholars. There is no modern dictionary definition which defines irony as coincidence, which is all that is being referred to in the article. I do not disagree with the word "irony" encompassing "situational irony", I disagree with using the word "irony" incorrectly, as it is in this article. I thought that my position was clear? My proposal was, from the very beginning, and still is, that the word 'irony' should be removed because it is used incorrectly. However I understand the futility of arguing with someone who wants to be right so badly that they provide definitions which clearly show them to be wrong but insist on the opposite. It's just not that important so I resign, congratulate you on your victory, and bid you good day sir! :-) FillsHerTease (talk) 19:03, 1 September 2014 (UTC)
- Naturally you ignored the dictionary definition’s continuation an outcome cruelly, humorously, or strangely at odds with assumptions or expectations because it does not suit your wish for the definition not to exist. Situational irony does not include “deliberate”; that is why it is situational. From Irony#Situational_irony: Situational irony, ... is most broadly defined as a situation where the outcome is incongruous with what was expected, but it is also more generally understood as a situation that includes contradictions or sharp contrasts. That’s precisely how the term is used in this article. Your continued insistence that I define irony to mean coincidence is inexplicable. Firstly, whether or not this particular situation is a coincidence is unknown, and secondly, it does not matter if the situation is the result of coincidence in order for it to constitute irony. From that section of the article on irony, Hinckley’s bullet striking Reagan as a consequence of the automobile being bullet-proof was a coincidence, but the outcome was ironic. In Gift of the Magi, the fact that both husband and wife sold their most precious possessions at the same time is a coincidence, but the outcome is ironic. Hinckley did not deliberately fire at the vehicle in order to strike Reagan. Neither the husband nor the wife in Gift of the Magi intended to derail each other’s gift-giving. Not just any coincidence is ironic, so no, I nor anyone else defines coincidence to mean irony. I really do not understand what you are not getting here, but at least we agree this conversation has lost any value. Strebe (talk) 23:54, 1 September 2014 (UTC)
- FillsHerTease -- I would not personally insist on the word "irony", but whichever word one chooses to use, there's a glaring discrepancy between Peters' sweeping grandiose rhetorical claims that "his" projection was more South-friendly than Mercator in every single way, and the reality that in one very prominent respect the Gall–Peters projection favors mid-latitudes (including much of Europe and most of North America) over tropical/equatorial regions (including most of Africa). Some (including myself) would be inclined to use even less flattering terminology. By the way, just yesterday I saw in a used bookstore a sociology textbook published in 2007 which had a world map using the projection (and it was just as ugly as it always is...) AnonMoos (talk) 11:38, 5 September 2014 (UTC)
- Could be a polite way of saying "hypocrisy", considering Peters' sweeping grandiose claims that his projection was the greatest thing since sliced bread in every way, and especially in being South-friendly... AnonMoos (talk) 18:16, 20 April 2014 (UTC)
- It could simply be an innocent failure to notice the effect of his choices. Since irony is in the eye of the beholder, it’s not only polite, it doesn’t come with the risk of being wrong. ;-) Strebe (talk) 22:51, 20 April 2014 (UTC)
The "In popular culture" section seems worthless to me
Neither seem interesting or notable to me, I think it adds little apart from clutter.Halfhat (talk) 22:34, 27 April 2014 (UTC)
There is a reference to this map projection type in the XKCD comic http://xkcd.com/977/ 104.12.204.201 (talk) 02:52, 2 December 2014 (UTC)
- Saw that, but not sure that it's relevant to anything but Munroe's personal opinions... AnonMoos (talk) 18:36, 2 December 2014 (UTC)
- Has it been referenced by any notable 3rd parties? HalfHat 02:11, 4 January 2015 (UTC)
- The West Wing mention crops up frequently in diverse quarters. Really, I’d just rather get rid of the whole section. It’s a magnet for trivia. Strebe (talk) 06:06, 8 January 2015 (UTC)
File:Gall–Peters projection SW.jpg to appear as POTD soon
Hello! This is a note to let the editors of this article know that File:Gall–Peters projection SW.jpg will be appearing as picture of the day on December 15, 2015. You can view and edit the POTD blurb at Template:POTD/2015-12-15. If this article needs any attention or maintenance, it would be preferable if that could be done before its appearance on the Main Page. — Chris Woodrich (talk) 23:48, 26 November 2015 (UTC)
- As usual, all good, Chris Woodrich. Thanks! Strebe (talk) 05:36, 2 December 2015 (UTC)
New subsection for adoption by UNESCO, Boston Public Schools?
The page and the projection have been the subject of renewed interest in the wake of the recent adoption of the projection by the Boston Public Schools (BPS; an article in The Guardian published on March 19th about the switch had over 2,000 comments and 75K shares on Facebook, as of April 17).[2] This development, and the claim that the projection has been adopted by UNESCO, are both featured in the current summary paragraph, but there is no further discussion of either pieces of info, i.e. in the body of the article. These details seem rather more relevant to the core topic than the pop culture mentions, such as they are. Okay to create a sub-section on adoption by UNESCO and BPS? Chicagoshim (talk) 23:02, 17 April 2017 (UTC)
- Thanks, Chicagoshim. I don't know of much to say about the UNESCO usage—at least, nothing I could cite. UNESCO publishes maps using the projection. Do you have references to reliable material that elaborates on it somehow, and in a way that aids understanding? As for Boston Public Schools, it made news recently, but Boston is a single school district among tens or hundreds of thousands in the world. The projection is used much more widely in UK school districts, and scattered others around the world. Is the article obliged to mention each one? If so, why? If not, why not, or why is Boston special?
- Please remove the sentence about the “Peters World Map”. The map is not the same as the projection. Also, you need to cite “most notably” as applied to the West Wing episode, or else remove it. Some people would claim XKCD is “most notable”; some would claim Oxfam’s usage is most notable, et cetera. I don’t know of any research that justifies calling this or that “most notable”. Strebe (talk) 00:33, 18 April 2017 (UTC)
References
- ^ Cite error: The named reference
Snyder2was invoked but never defined (see the help page). - ^ Joanna Walters (March 19, 2017). "Boston public schools map switch aims to amend 500 years of distortion". The Guardian. Retrieved March 19, 2017.
Wildly contradictory claims
The very start of the article reads: "The Gall–Peters projection is a rectangular map projection that maps all areas such that they have the correct sizes relative to each other." Then, the "Controversy" section pretty much completely dismantles this claim. Which is it? Bataaf van Oranje (Prinsgezinde) (talk) 23:25, 29 September 2017 (UTC)
- @Prinsgezinde:You haven’t established any contradiction. Please juxtapose the statements you believe to contradict each other. Strebe (talk) 17:35, 30 September 2017 (UTC)
- Really? That would be easier if it was just one.
- "Peters's chosen projection suffers extreme distortion in the polar regions, as any cylindrical projection must, and its distortion along the equator is considerable."
- "Several scholars have remarked on the irony of the projection's undistorted presentation of the mid latitudes, including Peters's native Germany, at the expense of the low latitudes, which host more of the technologically underdeveloped nations."
- "The claim of distance fidelity is particularly problematic: Peters's map lacks distance fidelity everywhere except along the 45th parallels north and south, and then only in the direction of those parallels."
- "No world projection is good at preserving distances everywhere; Peters's and all other cylindric projections are especially bad in that regard because east-west distances inevitably balloon toward the poles."
- "Such [rectangular] maps promote serious, erroneous conceptions by severely distorting large sections of the world, by showing the round Earth as having straight edges and sharp corners, by representing most distances and direct routes incorrectly, and by portraying the circular coordinate system as a squared grid."
- "The geographic and cartographic communities did not unanimously disparage the Peters World Map."
- If anything, claim it tries to have the correct size relative to each other. Bataaf van Oranje (Prinsgezinde) (talk) 23:32, 30 September 2017 (UTC)
- Really? That would be easier if it was just one.
- Really? That would be easier if anything in your list said anything about size disproportion. None do. Peters is an equal-area projection. There is no debate about that. It distorts distances; any projection does that. It distorts angles; any non-conformal projection does that. It has straight edges and sharp corners. It portrays the circular coordinate system as a square grid. You appear not to understand that projections have many kinds of distortions, despite that nothing in your list claims Peters distorts sizes. Strebe (talk) 01:51, 1 October 2017 (UTC)
- Strebe: Would you stop removing the tag while the discussion is still ongoing? Not only is it obstructive, doing so repeatedly counts as edit warring. You clearly know more about cartography but you need to remember that not every reader will. Saying all areas have the correct sizes relative to each other very much implies that the map is fully precise. Leaving out the bit about distortion (which changes the size we perceive) will confuse people:
- "Peters's chosen projection suffers extreme distortion in the polar regions,"
- "Several scholars have remarked on the irony of the projection's undistorted presentation of the mid latitudes, including Peters's native Germany, at the expense of the low latitudes, which host more of the technologically underdeveloped nations."
- "No world projection is good at preserving distances everywhere; Peters's and all other cylindric projections are especially bad in that regard because east-west distances inevitably balloon toward the poles."
- Equal area projection comes in many forms, and none of the other articles claim to show "correct sizes". Does the Werner projection show correct sizes? I assume your answer is yes, but in practice, we're looking at it in a way that it does not. Same goes for this one. Bataaf van Oranje (Prinsgezinde) (talk) 15:14, 1 October 2017 (UTC)
- @Prinsgezinde:Would you stop removing the tag while the discussion is still ongoing? Not only is it obstructive, doing so repeatedly counts as edit warring. → Adding the tag back into the article counts as edit-warring. Do you know what is obstructive? Adding spurious tags to articles before discussing them with the page’s editors and then getting insistent about it when you have little knowledge about the topic. Spurious tags undermine reader confidence in the article. They contribute to page churn. They waste reader time by causing potentially unbounded numbers of people to try to figure out what’s at issue and why, when there may be no issue at all. Editors are not obliged to coddle confused tagging. The dispute, if any, can get resolved on the Talk page without disrupting the article.
- Really? That would be easier if anything in your list said anything about size disproportion. None do. Peters is an equal-area projection. There is no debate about that. It distorts distances; any projection does that. It distorts angles; any non-conformal projection does that. It has straight edges and sharp corners. It portrays the circular coordinate system as a square grid. You appear not to understand that projections have many kinds of distortions, despite that nothing in your list claims Peters distorts sizes. Strebe (talk) 01:51, 1 October 2017 (UTC)
- Saying all areas have the correct sizes relative to each other very much implies that the map is fully precise. → It implies no such thing. That’s a fallacious deduction, and one that apparently few readers make, since no one has ever tried to claim the contradiction that you’re claiming in the much-debated, fifteen-year life of this article.
- Does the Werner projection show correct sizes? I assume your answer is yes, but in practice, we're looking at it in a way that it does not. → I have no idea what in practice, we’re looking at it in a way that it does not intends to mean. No. Werner and the Gall–Peters and the sinusoidal and Eckert IV and a bazillion other equal-area projections show correct relative sizes. Period. That’s what equal-area means. This is not a “perception” issue. True, people cannot estimate relative sizes to high accuracy (~5%) between different shapes, but that perceptive imprecision gets drowned out by the other kinds of distortions that Peters (and Werner and any other projection) introduce.
- I do not know how to say it any more plainly: There are many kinds of distortion. Correct relative sizes is only one kind of distortion. Therefore, even if you eliminate that one kind of distortion, that still leaves plenty of other kinds of distortion. If you are going to persist in reading distortion to mean only distortion of relative sizes, then you will persist in imagining contradictions where there are none. Strebe (talk) 17:23, 1 October 2017 (UTC)
- You're right, which is why I didn't engage you in it, but removing a tag when its discussion is still ongoing serves no purpose and is generally frowned upon. Whether you like tags or not, they're part of Wikipedia (and they're not a badge of shame). Articles like this usually aren't active enough to have someone respond so quickly so they're a way of getting the attention of other editors. Tags show that a contributor has found a problem with a page, one they should usually explain on the talk page, and tags can invite others to engage in the discussion. If it turns out other editors see no such problem the tag will be removed. However, you seem to want the article to be your way without attempting to build a consensus. Seeing the article's history, I'd commend you on your dedication to this article if you were more tolerant of other editors working on this article. It's somewhat understandable if you get annoyed by less knowledgeable people adding incorrect information but in this case (and several mentioned in other topics above) the problem is in how it comes accross. Wouldn't you admit that the average reader sees something like this differently than someone who spends a lot of time studying them? In any case, if we can now carry on with the actual discussion: I don't understand the remark about the "fifteen-year life of this article" because you only added in the part about "correct sizes" a little over 6 months ago. That really is the issue here. Why use this wording at all? It's not used in any other Equal-area article. To put it plainly myself: look at Australia on our images of the Werner and Gall-Peters projections. As you say, this difference is due to distortion. You also stress that every map projection suffers from this distortion. This is not understood by everyone, nor is the difference you keep stressing between size accuracy and controversial distortion. Bataaf van Oranje (Prinsgezinde) (talk) 21:42, 2 October 2017 (UTC)
- I do not know how to say it any more plainly: There are many kinds of distortion. Correct relative sizes is only one kind of distortion. Therefore, even if you eliminate that one kind of distortion, that still leaves plenty of other kinds of distortion. If you are going to persist in reading distortion to mean only distortion of relative sizes, then you will persist in imagining contradictions where there are none. Strebe (talk) 17:23, 1 October 2017 (UTC)
- @Prinsgezinde:removing a tag when its discussion is still ongoing serves no purpose. → I explained the purposes. You ignored them. To be more explicit: There was no emergency. The matter was under discussion here, where it is supposed to be discussed. I think they're not a badge of shame is naïve; the general public has no idea what those tags mean “internally”. They simply look alarming.
- However, you seem to want the article to be your way without attempting to build a consensus. → I want the article to be correct. If that’s not your way, well… . You set off a pointless fire drill, and you persisted after I clearly, neutrally explained why you were mistaken. Meanwhile, I monitor something like 200 articles. It’s a serious time drain to deal with people who want their pet discovery of nothing to be taken seriously and with full bureaucratic process. Look at how many words have been wasted on this nothingness. Is there some reason you could not have done a little due diligence after I posted this and before you posted this? I was fine enough until that posting, other than your ludicrous condescension in your previous posting with, Really? That would be easier if it was just one. How much time do you think is reasonable to impose on other editors if you’re not even willing to do a little homework? How reasonable is it to call me out for “how it comes across” when you yourself indulged in condescension before I departed from any kind of neutrality?
- I don’t understand your continued going on about “correct sizes relative to each other”. That’s not “jargon”. That’s plain, simple English. It’s there as an explanatory introduction to the term “equal-area”, which is jargon! Are you saying it’s better not to explain the jargon? Or… what? When I say no one noticed a contradiction for 15 years, it’s because the projection has always been described as equal-area, which, if “correct sizes relative to each other” is a contradiction, then so would be “equal-area”. Why does the “correct sizes relative to each other” explanation appear in this article? Because this article is far more likely to be visited by the general public than articles on other equal-area projections, and it’s also far longer and therefore explains far more things.
- nor is the difference you keep stressing between size accuracy and controversial distortion. → You have utterly lost me here. When did I mention anything about a “difference” between “size accuracy” and “controversial distortion” (when did I use that term?). When did I “stress” this “difference”?
- We all want a better Wikipedia. Next time, please consider the burden your actions impose and do some homework, rather than falling back on the infallibility of your own deductive powers. Strebe (talk) 01:13, 3 October 2017 (UTC)
Size is not the same as shape. "Equal area" is a property which can be very precisely defined, and which is mathematically true or false for any map projection. Shape distortion is a more complicated matter -- of course, no flat map can be completely free of shape distortion. AnonMoos (talk) 23:10, 5 October 2017 (UTC)
- True, which is why I was surprised to see Strebe's use of "correct". Calling the sizes correct is actually fine though as long as the lead also explains what its weaknesses are. Most people know very little about map projections and equal-area, which is why articles like this exist. "The Gall-Peters map shows the correct sizes of countries, but it also distorts them. Countries are stretched horizontally near the poles and vertically near the Equator, so although the size may be right, the shape definitely isn’t." This criticism needs to be addressed, as the lead currently barely describes anything from the huge controversy section and very much gives the idea that this map projection is without major flaws. That's not true. Cartographer Rob Lammle wrote: "Both projections are seen as flawed and have fallen into disuse as more accurate maps have been developed. In classrooms now, you're more likely to see the Robinson Projection or the Winkel Tripel Projection. The Gall-Peters map is still favored by some organizations, though many map publishers don't even produce it anymore." Numerous other cartographers said Gall–Peters is just as problematic as Mercator, and they pretty much all agree that better alternatives exist. In short: lead needs to include the negative. Bataaf van Oranje (Prinsgezinde) (talk) 14:39, 21 October 2017 (UTC)
- It is ·right there·:
The Gall–Peters projection is a rectangular map projection that maps all areas such that they have the correct sizes relative to each other. Like any equal-area projection, it achieves this goal by distorting most shapes.
- Strebe (talk) 16:35, 21 October 2017 (UTC)
- That's not negative. That's "this thing does this because it has to" without any of the specific criticisms raised against Gall–Peters. Prinsgezinde (talk) 20:10, 7 November 2017 (UTC)
- It is ridiculous to criticize a projection for its distortions; that is like criticizing the moon for looking round instead of spherical. The problem started when a charlatan reinvented the projection, gave it his own name, and made wild claims about it. The lede notes that the projection distorts (like any projection) and notes that the projection was the subject of major controversy. The details are in the body, where they belong. Strebe (talk) 20:36, 7 November 2017 (UTC)
- Strebe -- it's perfectly legitimate to criticize the use of a map projection for a specific purpose, when the distortions in the projection hinder its usefulness for that purpose. The Gnomonic projection is great for some things, but you wouldn't use it for a wide-area political map. Gall–Peters arguably has distortions which hinder its usefulness as a world map. AnonMoos (talk) 06:55, 13 November 2017 (UTC)
- @AnonMoos:Yes, it is, of course, legitimate to criticize misuse of a map projection. However, all map projections have distortions that hinder their use as a world map. The literature recognizes this fact, and hence the bulk of learned criticism of the projection itself (as distinct from Peters’s promotional activities) amount to æsthetics. In other words, it’s merely subjective. Strebe (talk) 06:43, 20 November 2017 (UTC)
- The resolution of the "seven North American geographic organizations" against all rectangular world maps implies that they didn't think it was a purely subjective matter of taste that non-rectangular projections could have advantages over rectangular ones... AnonMoos (talk) 12:35, 21 November 2017 (UTC)
- @AnonMoos: If you wish to move the conversation to my talk page or some other appropriate venue, I would be happy to discuss the many problems with the resolution, as well as direct you to scholarly criticism of the resolution (which should also be cited in the article). To repeat, the bulk of learned criticism has been about æsthetics. The resolution is not the bulk of learned criticism. Strebe (talk) 21:13, 21 November 2017 (UTC)
"All maps are political"
We currently have a line that states "Crampton sees the condemnation from the cartographic community as reactionary and perhaps demonstrative of immaturity in the profession, given that all maps are political". I'm not keen on the phrasing - I presume that "all maps are political" is part of what "Crampton sees", but it could be read as Wikipedia asserting that "all maps are political" (something that I would dispute, and which in any case would need a citation to support). User:Dasunt raised a similar criticism back in 2006, and while the wording has changed slightly since then, the broader problem remains. Crampton's paper is behind a paywall, so I can't see exactly what they say, but if "all maps are political" is their claim, then I would suggest rephrasing the sentence as "Crampton considers all maps to be political, and sees the condemnation from the cartographic community as reactionary and perhaps demonstrative of immaturity in the profession". Iapetus (talk) 12:48, 22 April 2021 (UTC)
- For reference, I found a downloadable PDF: https://www.researchgate.net/publication/240804475_Cartography's_Defining_Moment_The_Peters_Projection_Controversy_1974-1990. It seems like the line in question is the gist of hat Crampton is saying, and I think your suggested edit makes sense. Justin Kunimune (talk) 13:16, 22 April 2021 (UTC)
Proposed new section, on properties, advantages & disadvantages
Proposed Added Section, to go above the Controversy section, because objective properties, advantages & disadvantages are what matter.
Some Properties, Advantages & Disadvantages of Gall-Peters:
Advantages:
Due to its rectangular shape, & its great NS height for a given width, Gall-Peters (GP) is a very large map for its width. (Width is typically the limiting-dimension for a wall-map.)
Large map-area means more room for more detail, more labeling, &/or larger labeling.
And it's obvious that EW expansion, at all latitudes, to the map's full equatorial width, combined with large NS expansion, must and does increase scale at every point in every direction.
Large scale allows nearby points to be more easily resolved and distinguished.
.Size & scale are particularly important for working maps, as opposed to decorative maps.
In particular, classroom maps often or usually must be examined at a distance (from seat to wall)
Thematic maps in atlases must often be small in width, due to the need to show so many such maps in an atlas. That width limitation makes it particularly important to maximize area & scale for a given map-width.
Some Specifics:
. Region where scale is nowhere less than equatorial scale:
Between the latitudes 60 south & 60 north, from Antarctica to Oslo, Stokholm & Helsinki's approximate latitudes, on a GP map, there is no place where the scale in any direction is less than the scale along the equator. That's 87% of the Earth's surface That can't be said for other equal-area maps that are in use.
GP's area for a given width is about 1.62 times that of Mollweide, Hammer, & Goode Homolosine.
GP's area for a given width is 1.42 that Eckert IV.
...and likely similar for the similarly-shaped Eckert III, & Equal-Earth.
...with the greater average-scale that goes with that greater area.
GP shares the other usefulness-advantages of cylindrical projections in general:
With a position-&-properties ruler, it's easy to determine, on a cylindrical map, the following quantities:
Latitude, Longitude, scale & magnification (for a conformal map), and EW-scale, NS-scale &their ratio (for an equal-area map such as GP).
Cylindrical maps treat all longitudes equally.
Simplicity:
Cylindrical-Equal-Area (CEA), of which GP is an example, is the 2nd simplest equal-area map (The simplest is Sinusoidal, which isn't popular, due to its shape-distortion and low min-scale).
Using a simple diagram showing the horizontal projection of a sphere's surface onto a cylinder around the sphere in contact with its equator, the construction of CEA is easily demonstrated, and the reason for its equal-area property is easily demonstrated and explained.
Not so with other equal-area maps.
The equal-area property of Mollweide & Eckert IV can be demonstrated without calculus, but nonetheless requires a relatively elaborate geometric & algebraic explanation. Equal-Earth's construction, and why it's equal-area, are far too elaborate to explain to people.
Disadvantage:
Poor shapes at low-latitude.
...resulting in not-so-attractive or realistic appearance, and maybe some usage-inconvence in tropical-regions of the map, due to NS scales being up to twice EW scales.
GP isn't designed to win beauty-contests.
It goes without saying that (as with anything else) the advantages are available if one accepts the disadvantage.
All CEA maps have flattening in extreme north latitudes.
With GP, at lat 60, the ratio of point-max scale to point-min-scale scale is 2. That amount, or more, of shape-distortion at lat 60 isn't unusual for equal-area maps .
Comparison of GP's shape-merit with that of other CEA maps:
The Behrmann CEA map has a standard parallel of lat 30 instead of lat 45. The equatorward half of the the Earth is compressed EW,and the poleward half is compressed NS.
On Behrmann, at the equator, the NS scale is only 4/3 times the EW scale. On Behrmann, about 2/3 of the Earth is portrayed with that point-min/max scale of at least ¾...i.e. with shape no worse than at the Behrmann's equator.
That 2/3 of the Earth's surface extends, approximately, in the north, up to Barcelona, Spain; and to Garrison, New York, Omaha Nebraska, & Mount Shasta in California.
GP only achieves that ¾ point-min/max scale over 21% of the Earth's surface, from (in the Northern Hemisphere) the latitude of southernmost Tennessee, up to the latitude of Cambridge & Northampton in England, a bit north of London.
GP's strength is area & scale, not shape.
Of course Behrmann pays for that good tropical shape by increased high-lat shape-distortion. On Behrmann, at lat 60, the point-min/max scale is only 1/3, instead of GP's value of ½.
Behrmann's region with point-min scale greater than equatorial-scale is only the same 2/3 of the Earth in which it has point-min/max-scale greater than ¾. ...compared to GP's 87% of the Earth having point-min-scale greater than GP's equatorial scale.
As is well-known, CEA maps can't have good shapes at both high & low latitudes. Projections like GP, Balthasart or Tobler CEA, which have relatively good shape at non-polar high-lat, don't look as good at low-lat.
So, then, why not just use them only at high-lat, where they bring improvement?
e.g. It's at lat 41.41 that Behrmann starts having point-min/max scale less than ¾. So, stacked directly over a Behrmann map of the Earth, have a CEA map that has NS/EW scale = 4/3 at lat 41.41 ...and, with that map, map the region from lat 41.41 up to the north pole.
Do the same in the Southern-Hemisphere.
The result is a stack of 3 CEA maps, with point-min/max scale of at least ¾ over about 5/6 of the Earth's surface, from the tip of South-America up to Glasgow & Copenhagen.
...and with point-min-scale at least equal to equatorial-scale over about 90% of the Earth's surface, which extends from Antarctica up to about the middle of Iceland.
That high-lat CEA map with NS/EW scale = 4/3 at lat 41.41 is nearly the same as Balthasart. Its standard parallel is at lat 49.49
It goes without saying that different maps are best for different purposes. Scale & area improvements like GP or the above-described "CEA-Stack" are for working-maps, such as classroom-maps & thematic-maps, for which precise or distantly-observed detail is likely to be needed. But of course if a map is mainly decorative, or if a realistic picture of the Earth is what is desired, and accurate measurement or examination everywhere isn't important, then a more globe-realistic map like Mollweide would be desirable. 97.82.109.213 22:29, 3 August 2021 (UTC)
- all material on Wikipedia must be from reliable sources. if you have a source that lists advantages and disadvantages of the use of the gall-peters projection relative to that of specific other map projections, it may be worth including them. but right now, this looks like original research, which goes against Wikipedia's policies. Justin Kunimune (talk) 22:43, 3 August 2021 (UTC)
There's nothing wrong with copying & borrowing from sources. But something is very wrong when it's claimed to be disallowed to discuss Gall-Peters' advantages (only its disadvantage can be discussed) if a peer-reviewed source can't be cited.
Anyway, the important basic points in the proposed section consist of things much too obvious to require citation of a peer-reviewed source.
Wikipedia states that its rules aren't set in stone, and that there can be exceptions. Surely there's such an exception when the "rule" would allow discussion of disadvantages, but disallow discussion of advantages.
Properties-facts easily demonstrable by the known & usual principles of Cylindrical-Equal-Area maps aren't "Original-Research".
Anyway, I do have a Notable-Source. But first I re-emphasize that my proposed section contains two kinds of statements about fact:
1. Facts that are much to obvious to need citation of a "reliable source".
...such as what I said about the obvious relation between map-expansion & scale-increase. If you expand the map, or any part of it in one direction, making no change in the direction perpendicular to it, then obviously that will increase scales in some places, in all directions other than the one perpendicular to the explansion
And if you expand all of the map in both dimensions, that will increase scale at every point in all directions.
That's way too obvious to require a Notable Source.
...as is the fact that place-name labeling is easier to read if the lettering is bigger, and lettering can be bigger if map-area is bigger. ...and that determination of the geographical position of zone-boundaries in thematic-maps is easier if the map is bigger and the scale larger. ...and the fact that classroom ,maps are often or usually observed from at least partway across the classroom, from someone's desk to the wall.
2. Facts, about numerical map-properties over particular latitude-bands, require some calculation. If I determine and report such facts, you call it "Original Research". For one thing, that's really a misuse of that term, because it implies that I've discovered and studied a new area of study, and found out things that no one has previously known. No, the numerical specifics that I reported are about matters familiar to cartographers. ...nothing new or previously unknown.
And, anyway, as I said, I have a Reliable-Source. ...unless you want to say that Daniel Strebe is unreliable.
Strebe has demonstrated his willingness and motivation to refute Arno Peters' false-claims. He's evidently motivated to refute false claims that are in favor of Gall-Peters.
Therefore, if any of my numerical claims are false, Strebe will refute them.
...and, if he doesn't, that amounts to a statement from a Reliable-Source, that my numerical claims are correct.
Daniel Strebe is my reliable source.
We're indeed fortunate at this article, to have a reliable source at this article-page. -- 02:34, 4 August 2021 97.82.109.213
- 97.82.109.213 -- There a few interesting items in your list, but they're in the format of abbreviated personal notes (which are not appropriate to be cut-and-pasted into a Wikipedia article), and there seem to be some trivia items. You should also learn more about how Wikipedia talk pages work. I'm sure that Gall-Peters has many advantages over Mercator, but very few people are advocating for Mercator (though tradition or inertia has caused Mercator to be used in classrooms sometimes). Evaluating Gall-Peters as a general world map projection, it's certainly equal-area, but it's inferior to a number of other equal-area projections for world map use... AnonMoos (talk) 02:55, 4 August 2021 (UTC)
- Daniel Strebe is my reliable source. He's not your source, and he's not a reliable source. His published, peer-reviewed works are reliable sources. This conversation is not at all how Wikipedia works. We don't construct arguments and synthesize ideas for Wikipedia articles. These Talk pages are not soap-boxes for doing those things. Wikipedia articles are not permitted to make claims, even "obvious" claims, without citing reliable sources. Strebe (talk) 07:59, 4 August 2021 (UTC)
- Well, obvious claims can often be left uncited (as per WP:BLUE). personally, I'm less concerned with the list's factuality, and more with its length and subjectivity. for a list of this scale, deciding what to include and what not to include will always be subjective, and will thus always run the risk of pushing a point of view. that's what I mean when I call it original research, not that you have "found out things that no one has previously known", but that you have come up with original ideas that no one has previously published.
- I'm curious what you mean when you say that the rules "would allow discussion of disadvantages, but disallow discussion of advantages". It seems to me that the page already goes over a few of both, specifically as they are relevant to the surrounding controversy. are there specific disadvantages that you think are unfairly emphasized in the article as it is? Justin Kunimune (talk) 12:32, 4 August 2021 (UTC)
Strebe—
[quote] We don't construct arguments [/quote]
When responding to a request for a pros/cons section, one gives reasons pro & con. You can call that “constructing arguments”, but a pros/cons section is inevitably going to sound like “arguments”.
Here’s a quote from Wikipedia:
“Some sections do not have to be neutral. Examples include criticism sections and pro and con sections.”
Neither the “advantages” nor the “disadvantages” part of the proposed section can be “neutral”, and both inevitably will sound like “arguments”.
However, I stated both the advantages & disadvantages of GP…all the ones that I’m aware of. That’s neutrality. I didn’t ignore GP’s low-lat shape-problem, and the various kinds of resulting disadvantages.
[quote] These Talk pages are not soap-boxes [/quote]
I’ve been told that major changes to an article (such as a new section) should first be proposed at the talk-page, and that’s what I did.
[quote] Wikipedia articles are not permitted to make claims, even "obvious" claims, without citing reliable sources. Strebe (talk) 07:59, 4 August 2021 (UTC) [/quote]
Incorrect. You’re attempting an inappropriately legalistic use of WP policies, attempting to use them as rules that you can interpret to disallow mention of GP advantages. …to preserve the 1-sidedness of your article’s discussion. …about which a number of people here have commented.
Wikipedia says that an editor who wants to contravene the letter of a policy (they aren’t “rules”) must give reasons to justify that. I’ve been doing so.
1`. My numerical statements are easily verifiable, given that we have an in-house resident cartographer at this article.
2. Legalistic adherence to the source-citation suggestion would mean that GP’s advantages would be disallowed in the article. …not good, for a pros & cons section.
(See, below, the 1st sentence in Justin Kunimune’s reply.)
Obviousness is an instance of what is meant by WP’s advice to use common-sense instead of legalist application of policies as hard-&-fast “rules”.
I won’t quibble about whether or not you’re a “source”, even though, by the dictionary definition, you’re indeed a source or potential source of reliable information about maps. My point was that, given that we have an in-house resident cartographer at this article, that must affect the notion of “verifiability” here.
As I said, you’ve demonstrated the inclination & motivation to refute false statements that favor Gall-Peters, and an inclination to take the time to debate, for many pages, the meaning of “Irony”, and the grammatical difference between “Peter”, “Peters”, “Peter’s” & “Peters’”
Therefore, if the numerical facts in my section were false, you’d say so. You haven’t.
Due to your presence at the article, any objective facts that I state about maps, including the numerical facts in my proposed section, are indeed verifiable.
Justin Kuimune—
[quote] Well, obvious claims can often be left uncited (as per WP:BLUE). personally, I'm less concerned with the list's factuality, and more with its length and subjectivity. [/quote]
What??? A pros-&Cons section was requested, and I’ve listed, completely, the advantages & disadvantages that I’m aware of. …and you object that it’s too long? How about the long, long section on history & controversy? :D
[quote] for a list of this scale, deciding what to include and what not to include will always be subjective, and will thus always run the risk of pushing a point of view. [/quote]
I did my best to mention GP’s usefulness advantages, and the various kinds of disadvantages detrimental to beauty, realism & usefulness resulting from GP’s great low-lat shape-distortion. I emphasized GP’s low (21%) percentage of the Earth shown as shape-accurate as Behrmann’s equator (i.e. with point-min/max-scale of at least ¾).
I was clear that one wouldn’t choose GP for its shapes, beauty or realism.
And, yes, I spoke about GP’s often-important usefulness-advantages of large area & scale for a working-map.
[quote] that's what I mean when I call it original research, not that you have "found out things that no one has previously known", but that you have come up with original ideas that no one has previously published. [/quote]
Are you really going to claim that readability & practical usefulness of a big, vs a small, map, or big, vs small, map-scale, isn’t mentionable at WP unless there are publications about it? Could it be that some things are too obvious to devote journal-publications to? …but a pros-&-cons section for GP was requested, and I complied.
I suggest that the relation of readability & usefulness to map-size & map-scale aren’t an “original idea” that I’ve “come up with”.
…but rather just something too obvious to publish about in journals.
[quote] I'm curious what you mean when you say that the rules "would allow discussion of disadvantages, but disallow discussion of advantages". It seems to me that the page already goes over a few of both, specifically as they are relevant to the surrounding controversy. are there specific disadvantages that you think are unfairly emphasized in the article as it is? Justin Kunimune (talk) 12:32, 4 August 2021 (UTC) [/quote]
An excessively legalistic interpretation of a few WP policies (they aren’t “rules”) would disallow mention of unpublished, but grossly, blatantly, obvious GP advantages. And no, those advantages are NOT covered in the article, though GP’s shape-problem is well covered there.
That’s a bias and an imbalance, and a reason why the article needs an objective advantages/disadvantages section, such as the one that I propose.
AnonMoos-- If the format is too abbreviated, and the wording needs more filling-out, then I'll be glad to fill it out more. So let me know where.
Of course, for clarity, it's necessary to find a balance between detail & redundancy, vs brevity. I've tried to be as brief as possible, while still saying enough. But, definitely, let me know where I've erred too far in the direction of brevity.
I emphasize that I wasn't comparing GP to Mercator. I was comparing it to other maps that are advocated over GP. ...mostly equal-area maps (...though I mentioned Robinson & Eckert III too).
And I told of ways in which GP is better than other maps. ...but I also mentioned its disadvantage, because the proposed section is about both advantages & disadvantages. I wrote at some length about how the large low-lat scale-ratio is a disadvantage for realism, beauty, and even maybe for practical-use.
So GP is better than other maps in some way, and they're better than GP in other ways. And isn't that always how it is?
That's why I clarified for what uses GP is better, and for what other circumstances other, more realistic &/or beautiful maps would be desirable. -- 04:37, 4 August 2021 97.82.109.213
- IP 97.82.109.213 writes:
[quote] We don't construct arguments [/quote] When responding to a request for a pros/cons section, one gives reasons pro & con. You can call that “constructing arguments”, but a pros/cons section is inevitably going to sound like “arguments”.
- That argument, and the rest of them, do not fly in the face of Wikipedia policies. No, we do not construct arguments to include as material for the article text. The arguments we make are about the relevance and reliability of material from published sources. We make those arguments here, on the Talk page. We do not create pro/con lists invented by ourselves. If you can find reliable sources, then we can do what you propose. That’s really all there is to this. When I put “obvious” claims in quote marks, I did that for a reason: An observation anyone could make is one thing, and is permitted, but drawing conclusions about that observation is quite another thing, and it is not permitted. Wikipedia’s guidelines about “common sense” do not include the kinds of WP:SYNTH and WP:OR that you are talking about. Having been through various kinds of dispute resolutions about article content that is available to Wikipedia editors, I know that almost all of the edits you are talking about would surely fail if contested. Strebe (talk) 20:17, 4 August 2021 (UTC)
Strebe--
[quote] [quote] When responding to a request for a pros/cons section, one gives reasons pro & con. You can call that “constructing arguments”, but a pros/cons section is inevitably going to sound like “arguments”. [/quote]
That argument, and the rest of them, do not fly in the face of Wikipedia policies. [/quote]
If you’re saying that they do fly in the face of Wikipedia policies, I remind you that policies aren’t rules. Wikipedia says that editors wanting to contravene a policy must tell justification…as I have done in my most recent posts here.
I’ve told why this is an exceptional situation, for two reasons that I stated in a numbered-list, and I’ve told why exceptions to policy are justified.
Wikipedia says that it’s common for editors to misrepresent Wikipedia policies as hard-&fast “rules”, with no exceptions permitted, and to try to unjustifiably use them to prevent content that they disagree with or don’t like. [quote] No, we do not construct arguments to include as material for the article text. …We do not create pro/con lists invented by ourselves. [/quote]
I merely stated facts that are obvious to anyone, which is permitted by Wikipedia.
[quote] An observation anyone could make is one thing, and is permitted [/quote]
Good because that’s what I stated in my basic general non-numerical points.
[quote] , but drawing conclusions about that observation is quite another thing, and it is not permitted. [/quote]
I didn’t draw conclusions from the obvious observations. I merely stated them.
If you want to claim that I drew conclusions in my basic non-numerical points, then a specification of instances would be required.
[quote] Wikipedia’s guidelines about “common sense” do not include the kinds of WP:SYNTH and WP:OR that you are talking about. [/quote]
I trust that you understand that a serious challenge would have to be a lot more specific than that.
https://en.wikipedia.org/wiki/Wikipedia:You_don%27t_need_to_cite_that_the_sky_is_blue
As I said, my general basic points state facts that are obvious to anyone, and don’t depend on constructing synthesis or drawing conclusions from them.
And I repeat that my numerical statements in the proposed section are all verifiable…You, Strebe, could verify or refute them. …or are you less “Notable” than some newspaper reporter & editor who don’t know squat about their topic?
You aren’t going to? Fine. Wikipedia’s verifiability policy doesn’t call for actual verification. Mere verifiability is sufficient.
- The unsigned editor writes: I merely stated facts that are obvious to anyone, which is permitted by Wikipedia. They’re not obvious. Practically all of your claims are false, debatable, or else the significance is debatable. In other words, not obvious. This is why original research and synthesis are not permitted. If the points you are making were important enough to matter, you would find these points being made in citable literature. They’re not. That means they do not meet Wikipedia’s threshold for inclusion. To illustrate with your first five points:
- Due to its rectangular shape, & its great NS height for a given width, Gall-Peters (GP) is a very large map for its width. (Width is typically the limiting-dimension for a wall-map.)
- With “large” undefined here, I don’t know what that intends to mean. You state, without evidence, that width is typically the limiting factor for a wall map. I disagree, and I also disagree that wall maps are necessarily what is important.
- Large map-area means more room for more detail, more labeling, &/or larger labeling.
- Not so. As an equal-area map, Gall–Peters has exactly as much area as any other equal-area map. The massive left-right stretching in the mid- and higher latitudes is negated by increasing top-bottom compression toward the poles; likewise, the vertical stretching in the low latitudes is negated by the east-west compression.
- And it's obvious that EW expansion, at all latitudes, to the map's full equatorial width, combined with large NS expansion, must and does increase scale at every point in every direction.
- This is not only not obvious; I cannot even tell what you mean. Every map projection distorts scale. To claim “in every direction” is to claim something apparently false, since north-south compression on Gall–Peters increases infinitely at the poles such that the scale in the north-south direction at the pole is zero rather than 1.
- Large scale allows nearby points to be more easily resolved and distinguished.
- It doesn’t have “large scale” by any meaning I know of. Severe north-south compression in the high latitudes ensures that points oriented vertically are less easily resolved (than… what?).
- Size & scale are particularly important for working maps, as opposed to decorative maps.
- It depends on what kind of work, so this statement is also debatable and definitely wrong in some circumstances.
- There is nothing special about these five points; most of the others are similarly debatable. The fact that these points are debatable and not cited means they cannot properly be made in the article. More to the point, if a pro/con list were something important enough to be included in the article, then such lists could be found in the literature and properly cited instead of argued about here, which is not supposed to happen. Strebe (talk) 02:18, 7 August 2021 (UTC)
[quote] The unsigned editor writes: I merely stated facts that are obvious to anyone, which is permitted by Wikipedia. They’re not obvious. Practically all of your claims are false, debatable, or else the significance is debatable. In other words, not obvious. [/quote]
My main point was that a larger map is easier to use, to examine places, to judge or measure distances, to determine the geographical-position of a zone-boundary on a thematic map, to read the labeling, etc.
False? Debatable original research? Debatable significance. You’re joking, right?
That’s obvious common-knowledge. It’s why atlases with large page-area are printed & purchased, in spite of their relatively-higher price. A pocketbook-size atlas would be considerably less useful than one with the more typical large page-area.
It’s why publishers print, and people buy, roughly 5’X3’ wall-maps instead of postcard-size wall-maps.
How’s all that for original-research? Shall I name it after myself? :D
[quote] If the points you are making were important enough to matter, you would find these points being made in citable literature. They’re not. [/quote]
As I’ve already explained here, some things are too obvious to need or justify journal-articles. …and therefore are not “citable”. Is there a journal-article to cite that it’s unwise to lie down in the bottom of a space that’s being filled with concrete, or that you get more exercise by lifting 15 pounds than 2 ounces…so it can’t be said in a Wikipedia article? :D
And you say or imply readability and usefulness are unimportant. :D
That’s a bizarre claim to make.
[quote] That means they do not meet Wikipedia’s threshold for inclusion. [/quote]
It means that you’re playing fast-&-loose and creatively with Wikipedia’s policies.
[quote] To illustrate with your first five points: • Due to its rectangular shape, & its great NS height for a given width, Gall-Peters (GP) is a very large map for its width. (Width is typically the limiting-dimension for a wall-map.) With “large” undefined here, I don’t know what that intends to mean. [/quote]
Merriam-Webster: “Large: 4a Exceeding most other things of like kind, especially in size or quantity.”
“Size: Physical extent, magnitude, or bulk..”
The kind of “extent” referred to for maps is their area.
Instead of making you look up “area”, I’ll just say that the area of a rectangle is determined by multiplying its length by its width (qv). …and that, for non-rectangular plane-regions, the areas of infinitesimal rectangles (or sometimes triangles) within a region are often summed to determine the area of a non-rectangular plane region.
Area is expressed in linear units squared. e.g. square inches or square centimeters.
[quote] You state, without evidence, that width is typically the limiting factor for a wall map. I disagree. [/quote]
Well, look at a map on a wall. Above or below where it’s mounted, one wouldn’t place a map. We don’t place maps up adjacent to the ceiling, or down adjacent to or near the floor. Therefore maps and other wall-posted things don’t compete for vertical-space, and so their vertical dimension isn’t their fit-critical dimension (their dimension that determines whether they’ll fit in a particular space.
And, additionally, for nearly all maps in equatorial-aspect mounted with equator horizontal, the width is considerably greater than the height.
[quote] …and I also disagree that wall maps are necessarily what is important. [quote]
They’re often important, as in classrooms.
But atlases often have small thematic maps vertically stacked on a page. They adjoin eachother on edges that are (at least roughly) parallel to their equator, parallel to their X dimension. They don’t adjoin eachother along edges parallel to their Y-dimension. So their width is limited by the width of the page, and each map’s area depends on its space-efficiency (fraction of the map’s circumscribing-rectangle that the map fills) and the variable consisting of the map’s height (Y-dimension).
If the book doesn’t need so many such maps as to tax the books page-capacity and make it too thick, then the area of the maps depends on their area for a given width. Often it’s convenient to calculate that quantity by dividing their space-efficiency by their aspect-ratio.
If the number of those small thematics maps needed is so great that they threaten to make the atlas require too many pages, then space-efficiency itself could become the critical map-quantity that limits the feasible combined-area of the maps.
…but, otherwise, the critical map-quantity is area for a given width.
[quote] Large map-area means more room for more detail, more labeling, &/or larger labeling. Not so. [/quote]
What a funny thing to say. Can you justify that strange claim?
[quote] As an equal-area map, Gall–Peters has exactly as much area as any other equal-area map. [/quote]
Yes, it maps the same planet, and therefore a planet with the same area.
World-maps differ in area. A world-map could be printed the size of a postage-stamp, or could cover a wall of a large room.
In equatorial-aspect, with the X-dimension as the width, and for a given width, a Gall-Peters (GP) map has more area than any other world-map that has been used to any significant degree.
…much more area.
…because of its maximal space-efficiency (unity), and its very low aspect-ratio.
Or if you’re just looking at how much area a map has as a percentage of the area of its circumscribing-rectangle, then of course that’s what I call “space-efficiency”, and the cylindrical equal-area projections collectively beat nearly all of the other equal-area maps. (…other than the few rectangular non-cylindrical projections, whose construction is far too complicated to offer to the public).
[quote] The massive left-right stretching in the mid- and higher latitudes is negated by increasing top-bottom compression toward the poles; likewise, the vertical stretching in the low latitudes is negated by the east-west compression. [/quote]
Yes, an equal-area map doesn’t magnify some regions more than others.
And, on an equal-area map, a point with greater X scale has proportionately less Y-scale. It’s intuitively obvious that there’s a cancellation of effects there, and a sense in which overall scale is unchanged.
In fact, the geometric mean, over all the points on the map, and all directions at each point, is proportional to the square-root of the area of the map. (more detail below about that.)
But it isn’t necessary to say that in the proposed section, because the cancellation between the expanded & shrunk scales at a point on an equal-area map is intuitively obvious.
(The points considered don’t include the pole, because, for most equal-area maps, there’s an infinite scale there, and an infinite scale can’t be represented by a number.)
Gall-Peters (GP) , with its maximal space-efficiency, and its low aspect-ratio, achieves a much greater area for a given width than other comparably-widely-used equal-area world-maps.
[quote] • And it's obvious that EW expansion, at all latitudes, to the map's full equatorial width, combined with large NS expansion, must and does increase scale at every point in every direction. This is not only not obvious; I cannot even tell what you mean. Every map projection distorts scale. To claim “in every direction” is to claim something apparently false, since north-south compression on Gall–Peters increases infinitely at the poles such that the scale in the north-south direction at the pole is zero rather than 1. [/quote]
All or most equal-area world-maps other than pointed-pole maps such as Collignon, Sinusoidal, Craster-Parabolic, and Quartic-Authalic, have infinite-scale and zero-scale at the poles.
.e.g. Mollwide, Eckert IV, and Equal-Earth do.
So, when I spoke of increasing the scales in every direction at all points, yes that’s untrue at the poles. For most equal-area maps, there remain zero scale and infinite scale at the poles.
So yes, add “except at the poles” to what I said.
1. Double the linear dimensions of any map, while keeping its original proportions, and you quadruple its area. i.e. Its area is proportional to the square-root of its dimension, when the shape & proportions are unchanged.
Likewise,it’s obvious that any linear distance on the map, anywhere, in any direction, on the map, will also increase in proportion to that uniform increase in the map’s dimensions…and in proportion to the square root of the map’s area.
That’s for a map that changes only its linear measurements, uniformly, with no change in shape or proportions.
2. What about different equal-area cylindrical or pseudocylindrical maps with the same area?
Say we start with some non-cylindrical pseudocylindrical world-map. Say, just for example, it’s a Sinusoidal map. …but it could be any non-cylindrical pseudocylindrical.
Starting at the equator, divide the NE quadrant of the map into very many very thin east-west rectangular lat-bands parallel to the equator.
Starting with the lat-band directly above the equator, expand it to the full width of the equator. Because we want to keep equal-area, that rectangular band must be shrunk in the Y-dimension by the same factor it’s expanded by.
Then do the same with the next ultra-thin lat-band above (north of) the previous one. …and so on, for all the stacked ultra-thin lat-bands of the entire NE quadrant of the map.
The result is a Cylindrical Equal-Area map having the same area as the initial pseudocylindrical map. What about the geometric mean of the scales.
Because equal-area must be maintained, when a rectangle representing a particular part of the Earth on the map is expanded in one dimension, it must be shrunk in the mutually-perpendicular direction.
It can be shown that, at any point, when the scale there is increased in one direction, and decreased by the same factor in the mutually-perpendicular direction, then, for any direction whose scale is increased, there’s another direction in which the scale is decreased by the same factor.
…meaning that the geometric-mean of the scales in all the directions at that point is unchanged.
…and that the geometric-mean of all the scales at all of the points in that rectangle is unhanged.
…and that the geometric mean of all the rectangular ultra-thin lat-bands that I mentioned on that map is unchanged.
…and that the area of the entire NE map-quadrant is unchanged.
Each of the ultra-thin lat-bands was kept to constant area, and so the area of the whole map-quadrant hasn’t changed. So, constant area for an equal-area map means constant geometric-mean, over all the points on the map, and over all the directions at each point, of the scale.
So GP’s much greater area for a given width means a much greater average (geometric-mean) scale for a given width.
…just as bigger scale is intuitively obvious for a bigger map.
And yes it’s intuitively obvious that making a map will make its average scale bigger.
• [quote] • Large scale allows nearby points to be more easily resolved and distinguished. • [/quote]
It [Gall-Peters] doesn’t have “large scale” by any meaning I know of. >p> GP has large mean scale. …referring to the geometric-mean, over all points on the map (except the poles), and over every direction at each point. That geometric mean is proportional to the square-root of an equal-area map’s area.
For a given map-width, do you know of any other widely-used equal-area map with as high a geometric mean scale (averaged over all points on the map, and over all directions at each point)?
GP also has point-min-scale at least equal to its scale along the equator, all the way from lat 60 south, up to lat 60 north. Can you name another widely-used equal-area map for which that can be said?
[quote] Severe north-south compression in the high latitudes ensures that points oriented vertically are less easily resolved (than… what?).
It’s intuitively obvious that a bigger map has bigger average-scale. And it can be demonstrated that the geometric-mean, over all points on the map (except the two poles), and over all directions at each point, is proportional to the square root of the map’s area (…as expressed in square-inches or square-centimeters).
[quote] • Size & scale are particularly important for working maps, as opposed to decorative maps.
It depends on what kind of work. [/quote]
How about the kind of work that requires the map to be readable and its labeling to be legible?
- D
I made it quite clear that I was referring to map-use that involves precise measurement or examination, or distant-viewing (as from a desk to a wall-map in a classroom).
[quote] , so this statement is also debatable and definitely wrong in some circumstances. [/quote]
See above.
I never said that one never uses a map other than at a great distance, and in a way that doesn’t require close measurement or examination.
In fact, I said that for a primarily decorative map, or when one prefers realism to other considerations, a more globe-realistic map such as Mollweide would be desirable.
[quote] There is nothing special about these five points; most of the others are similarly debatable. [/quote]
All of your objections were answerable.
[quote] 1The fact that these points are debatable and not cited… [/quote]
They aren’t debatable, and are too obvious to require citation. …just as you’ll never find a citatable journal-article about the fact that “square” and “not-square” aren’t the same. So you wouldn’t let a Wikipedia article state that either?
[quote] More to the point, if a pro/con list were something important enough to be included in the article, then such lists could be found in the literature. [/quote]
You’ve got to be kidding.
The pros & cons of anything intended for any important use, including a map-projection, are important.
If you think it should be in “the literature”, then write it there.
I don’t claim to know or care why someone does or doesn’t write something, or why someone dislikes something so much that he doesn’t think it merits a pros-&-cons discussion. It’s none of my business, and it’s irrelevant to the merits of GP.
But shall I speculate?
I’m not criticizing the people who write “the literature”, but just maybe they don’t like Gall-Peters, due to its unaesthetic and unrealistic low-lat shapes. Sure, I don’t like its low-lat shapes either. But some might feel that that’s a reason why GP doesn’t deserve a pros-&-cons listing, because, **in their own subjective-judgment**, it’s entirely unacceptable, &/or is merits-dominated by all other equal-area world-maps, due to its bad low-lat shapes.
Maybe GP’s unpopularity among the other cartographers would deter a cartographer from mentioning that it has an advantage. One must think of one’s reputation.
…merits-dominated by all other equal-area world-maps because GP (in some people’s perception) has no advantages to justify its use, given its bad low-late shapes & unrealism.
And (just speculating) maybe GP’s unpopularity among the other cartographers would deter a cartographer from mentioning that it has an advantage. One must think of one’s reputation.
And certainly the shenanigans of Arno Peters, his false-statements, his claim of priority for Gall-Orthographic, and for equal-area maps in general…maybe those decidedly un-academic-like acts has strongly prejudiced academia, to the extent that any academic would be embarrassed to speak of GP having an advantage, for fear of seeming to support the academically-unpopular Arno Peters.
Look, your article about Gall-Orthographic REEKS of POV. Not only do you refuse to allow mention of Gall-Orthographic’s advantages, citing some inapplicable and invalid legalistic-claim that misinterprets Wikipedia policy…but you also fill the article about Gall-Orthographic with irrelevant prejudicial material about the antics of some who didn’t introduce it :D
Talk about bias, and POV!
Most articles about a map-projection are only about the projection. You fill your article with (as I said) voluminous irrelevant and prejudicial material about Arno Peters—who wasn’t even the introducer of the map.
Alright, I’ll claim that I invented the Mollweide Projection. Now you have to fill the Wikipedia article with information about my false claim that I invented Mollweide, and whatever false claims I choose to make about it.
…Oh, what’s that? You say that the only reason you won’t do that is because I don’t have Arno Peters’ publicity connections, savvy, & ready-opportunity?
The Gall-Peters article needs thorough overhaul. Add pros & cons, and move all the Peters history, & controversy to the Arno-Peters page. He’s famous enough to rate a Wikipedia page about him, but not enough to dominate the article about Gall-Orthographic, which he didn’t introduce.
All that derogatory scandal-history with which you’ve stuffed the article about Gall-Orthographic is intended to discredit James Gall’s Orthographic projection by tying Arno Peters to it.
Your article intentionally confuses academic reaction to Peters’ false claims, with the merits of the map itself.
Well guess what: GP does have advantages, and I’ve named some of them. And they’re blatantly, grossly obvious.
I’ve described them in general, and I’ve specified them quantitatively.
- While I don't disagree with any of your points factually, I do continue to think that most of them are trivial or of debatable relevance. Your point about the Gall-Peters projection's area is true, given the assumptions you have laid out. But I don't think that width is the only important dimension for a poster. That's why we don't place posters adjacent to corners, and why posters are usually landscape even when they don't have to be. Furthermore, the efficiency with which a map fills a rectangle does not vary much across projections. A rectangle can fill a poster or a page with 100% efficiency, and a projection like Mollweide, which is not space-efficient at all, fills the same with 79% efficiency. That means that on average, point elements on a rectangular map projection are only 11% farther away from each other than the same points on a Mollweide projection that fills the same rectangular area. I think that's too small to mention. To state my personal opinion, I don't think the Gall-Peters projection has any redeeming qualities for any purpose when compared to other equal-area projections. More to the point, I think reliable sources omit these things because they view them as minor or irrelevant, not because they are too obvious.
- Relatedly, the current article does not violate WP:POV, because it accurately represents the points of view expressed in the reliable sources. This projection is basically only ever mentioned nowadays in relation to Arno-Peters and the controversy surrounding him (and I don't think it makes sense to create a Wikipedia page for him because he is only ever mentioned for his role in that controversy---see WP:ONEEVENT). Your counterexample about Mollweide doesn't hold, not because of publicity connections or savviness, but because you are not mentioned in reliable sources. If a major news agency propagated your claim that you created Mollweide projection, then we would probably add that to the Mollweide page.
- I see how that may be prejudicial against this particular map projection, but such is the nature of Wikipedia. If the reliable sources think something isn't important enough to mention, then Wikipedia won't mention it either, even if the editors think it is important. That's pretty clearly laid out in WP:ADVOCACY. It isn't a perfect policy, but it minimizes the amount of subjective debate among editors about what is and isn't relevant.
- P.S. if you add four tildes at the end of your post, Wikipedia will automatically add a signature, which makes it easier to read.
- Actually, I take some of that back. I found this Oxford Cartographers page that lists advantages of the projection:
- So I think the things they list here are sourced well enough to include. Namely, they mention
- that it is equal-area
- that meridians are straight lines
- that parallels are straight lines
- that equal-area map projections are more fair.
Justin--
Thanks for the reply. I guess it’s a matter of individual preference. For me, subjectively, for some applications, a little practical-advantage outweighs a lot of unrealism & ugliness. But of course to each their own. I’m delighted by GP’s amount of use.
And, anyway, again it’s just a matter of personal opinion, but I feel that Wikipedia is way too cautious about crackpots. I feel that content should be judged on its own merits, and that the matter of whom it’s from is relatively irrelevant.
I’d like to mention an extreme case as an example. As you know, there have been numerous authors who advocate very questionable archaeological theories. One of them, among the other things he said, suggested that the Vernal-Equinox was in Leo in 10,000 BC or 10,500 BC (I don’t remember which). An astronomer (a notable person) said that it wasn’t in Leo in that year. He justified his claim by saying that Planetarium software said so. But the R.A. & declination co-ordinates that he gave for the Vernal-Equinox’s position in that year was exactly, right to the arc-second (or whatever precision it was given in), the position that it would have had if precession had had its *current* rate all the way back to 10,000 BC. But it didn’t.
By a graph of precessional rates over that duration, from a very esteemed & notable expert source (maybe Laskar), and based on the proper-motion of the stars in Leo, I determined that, in the year in question, the Vernal-Equinox was indeed in Leo. It was inside the triangle that forms Leo’s rump, at the rear (east) end of Leo.
The astronomy professor had, erroneously or intentionally, given an incorrect position based on planetarium software that was using an obviously wrong precessional-rate. That astronomy prof, a notable-source, was talking pseudoscience bull-____. But Wikipedia insisted on taking his word for it, and not allowing any mention of the obvious questionableness of a Vernal-Equinox position that precisely matches the position given by assuming that today’s precessional-rate has always obtained. It was impermissible to mention that.
I pointed out, to whoever was answering communications, that they needn’t take my word for it. All that’s necessary would be to look at the position given for the Vernal-Equinox by planetarium-software that assumed constant precessional-rate at the current-value. But no. Evidence doesn’t count. Whatever a “notable” person says is sacrosanct and not to be questioned, even by looking at obvious readily-available evidence.
I don’t believe the archaeology-charlatan’s theories, but I didn’t like it that easily demonstrable pseudoscience from a “Notable” person trumps readily-available evidence that anyone can check, regarding the astronomy prof’s claim about where the Vernal-Equinox position in 10,000 or 10,500 BC.
...that a notable astronomer could say pure obvious pseudoscience, and no one was allowed to mention the, available-to-all, evidence that makes his statement more than a little questionable.
Sure, he wanted to debunk a charlatan, but it shouldn’t be done with the use of falsity & pseudoscience.
I mention that episode because it shows that a notable source isn’t really always a reliable source.
- I agree, it's very easy to Wikipedia to propagate false information by blindly following sources it deems reliable. A real encyclopedia would have a small number of paid editors to do checks like you describe. But on a public platform with millions of volunteers, allowing anyone to check claims just leads to a lot of uninformed arguing, edit wars, and—I would wager—more misinformation overall. Justin Kunimune (talk) 02:19, 9 August 2021 (UTC)
Justin—
Well, I fear that Wikipedia isn’t going to allow the experiment that would resolve that wager.
About wall-maps’ fit-critical dimension:
Let me re-emphasize this: Look at a wall-map, at the space above & below it. Would you want to put a map there? No one wants a wall-map, or any other wall-posted thing, to be up adjacent to the ceiling, or down near the floor. Therefore that space isn’t used, and is available for the map’s vertical-dimension. There’s room to have the map’s vertical dimension as large as you want. Gall-Peters? Sure. Square Tobler CEA? Sure.
I admit that there could be some book-page situations where a map’s X-dimension might not be its fit-critical dimension. But, as I mentioned in a previous post, for those little thematic maps, several to a page, that some atlases have, it can be convincingly argued that their fit-critical dimension is their X-dimension, unless there need to be so many pages of them that they threaten to make the atlas too thick. …in which case pure space-efficiency might become more relevant.
Another thing:
For both Sinusoidal and Lambert CEA, the average (geometric-mean) scale over the whole map (except at the points at the poles), in every direction, is exactly equal to the scale along the equator.
…suggesting that there’s something significant & special about the equatorial-scale, the scale along the equator.
I refer to the geometric-mean of scale over the map, in every direction, referenced to, expressed in terms of, the scale along the equator, as “av-scale”.
So Sinusoidal & Lambert CEA have av-scale of unity.
Most equal-area projections have av-scale greater than unity.
An exception is Collignon, which has av-scale of only .89
Here are the av-scale values for some equal-area projections:
Sinusoidal: 1
Lambert CEA: 1
Behrmann: 1.155
Mollweide: 1.111
Eckert IV: 1.184
Gall-Peters: 1.414
-- Above comment by User:97.82.109.213
@97.82.109.213:, I think you need to review some basic Wikipedia policies and guidelines:
- No original research -- Wikipedia doesn't publish its editors' own analyses, but only reports on what reliable sources say about a topic. It shouldn't be hard to find some reputable source that covers the issues you mention above.
- Collaboration with other editors is the way to get things done.
- Talk pages are for productive discussion about the article, not for treatises on the subject-matter of the article.
- Concision is valued--don't write long, repetitive posts on Talk. I would add: format your contributions so that they're more structured and thus easier to read.
A more minor, but still important WP standard:
I certainly agree with you that the article needs to talk about both the advantages and the disadvantages of Gall-Peters, and I look forward to your contributions in that direction... but you need to follow Wikipedia's policies and guidelines to move that forward. Thanks, --Macrakis (talk) 20:16, 10 August 2021 (UTC)
Makrakis—
• [quote] • No original research -- Wikipedia doesn't publish its editors' own analyses, but only reports on what reliable sources say about a topic. I • [/quote]
We’ve been over that. In my proposed section, I didn’t include “Original-Research”. I merely stated facts that are obvious to anyone, and to which the “Original-Research” & “Verifiability” exclusions don’t apply. …and quantitative statements that are easily verifiable, because they could be easily verified or refuted by Strebe, an in-house resident cartographer at this article.
And, as I've mentioned, Wikipedia policy doesn't emphasize verification itself, but rather mere verifiability--the availability of accuracy determination, should it be desired.
You’re applying Wikipedia policy in a manner different from what Wikipedia's written guidelines and policy-explanations say.
• [quote] • t shouldn't be hard to find some reputable source that covers the issues you mention above. • [/quote]
As Strebe pointed out, most cartographers aren’t interested, probably because there seems to be a rule that the only relevant standards for comparison of equal-area projections consist of various ways of expressing difference the maps’ point-max-angular-error (its global-average, zonal values, global-max, etc.). ...and because, as Justin Kunimune suggested, most cartographers’ subjective feeling is that the usefulness-differences are too small to matter.
I’ll just add here that, from what I’ve read, Walter Behrmann said that Behrmann CEA has less average point-max-angular-error than any other equal-area world map-projection. •
• [quote] • Collaboration with other editors is the way to get things done. • [/quote]
I didn’t say or imply otherwise. Of course I value suggestions and additions, and there’s no reason to suggest otherwise.
[quote] Talk pages are for productive discussion about the article, not for treatises on the subject-matter of the article. [/quote]
My post today was discussion about the merit and justification of things that I said in my proposed section. …i.e. things relevant to the article itself.
It was a reply on the matter of whether map-width &/or equatorial-scale is a good reference-quantity.
…and support for things that I said in my proposed section. •
• [quote] • Concision is valued--don't write long, repetitive posts on Talk. • [/quote]
TV has conditioned many people to want soundbites, but some topics aren’t well addressed in that way. But, if something can be said briefly, then of course that's how I want to say it. •
• [quote] • I would add: format your contributions so that they're more structured and thus easier to read. • [/quote]
I didn’t ignore structure, and I tried for clarity. But I always welcome comments & suggestions that would improve clarity and brevity. A problem with brevity is that it can reduce clarity. A balance must be sought between brevity & sufficiency of explanation & expression. As I said, I welcome suggestions & comments.
- The IP editor writes, And, as I've mentioned, Wikipedia policy doesn't emphasize verification itself, but rather mere verifiability--the availability of accuracy determination, should it be desired.
- From the first sentences of WP:VERIFIABLE:
In the English Wikipedia, verifiability means other people using the encyclopedia can check that the information comes from a reliable source. Wikipedia does not publish original research. Its content is determined by previously published information rather than the beliefs or experiences of editors. Even if you are sure something is true, it must be verifiable before you can add it.
- In other words, verifiability doesn’t come from the kinds of original research that the IP editor advocates, nor that editor’s beliefs or experiences, and isn’t from calculations or analysis that someone could conceivably make. It’s from a reliable, published source, the definition of which is given in WP:RELIABLE. Strebe (talk) 21:28, 10 August 2021 (UTC)
Strebe--
″it must be verifiable before you can add it."
Of course. My numerical-statements in my proposed section could be verified (or refuted) by you. ...could be verified. That's what matters. You could choose to say whether they're correct or incorrect. ...or not, as you choose. But the relevant fact is that you could.
...and if you said that they're correct, then there wouldn't be any concern that readers would be misled by false statements in the article. ...and if you don't say, it remains that the statements are verifiable, meaning that they could be verified if desired. -- Above comment by User:97.82.109.213
- Please learn how to use formatting commends like ":" at the beginning of the line. "[quote]" is not proper WP formatting and results in hard to read text.
- Of course brevity and fullness of expression need to be balanced. You are not balancing them. Repeating the same statement multiple times is not fullness of expression.
- You are misunderstanding verifiability. It is about the verifiability of a source, not the verifiability of a fact.
- Oh, and as you've been told before, please sign your contributions.
- Thanks, --Macrakis (talk) 23:39, 10 August 2021 (UTC)
- Please learn how to use formatting commends like ":" at the beginning of the line. "[quote]" is :not proper WP formatting and results in hard to read text.
Will do! I assume that the colon must be added to the beginning of each line. It would be a convenient way to copy when replying in Word, without having to do the copying-procedure at the Wikipedia editing-space.
- Of course brevity and fullness of expression need to be balanced. You are not balancing them. :Repeating the same statement multiple times is not fullness of expression.
I’m not sure whether you’re referring to my proposed section, or to my replies at this talk-page.
If you’re referring to the proposed section:
Though maybe, sometimes, one repetition is alright and can be helpful if it’s unobtrusive, and called-for for a reason such as a seeming-contradiction, I agree that it’s undesirable to repeat something so as to put readers off.
I said that I was interested in suggestions, and so there’s no need for your hostile tone, and implied claim of uncooperativeness that accompanies your suggestion.
If you’re referring to the talk-page:
I won’t deny that, when answering the same objection, I give the same answer.
- You are misunderstanding verifiability. It is about the verifiability of a source, not the :verifiability of a fact.
]Verifiability is about verification being possible. Look it up.
Yes, ordinarily the only readily-available verifiability is via citation of a notable (most definitely not necessarily reliable) publication.
But Wikipedia’s written guidelines recognizes & emphasize that circumstances aren’t always usual, and, when they aren’t, the guidelines aren’t hard-&-fast rules. I mentioned that before, but evidently it didn’t sink-in.
Wikipedia’s policy guidelines aren’t meant to be made-into, and used as, graven-in-stone, dogmatic, literalist, fundamentalist, quasi-religious doctrine.
Wikipedia’s written guidelines have been quite explicit about that, as you well know.
At the risk of being criticized for repetition evidently it’s necessary to repeat this:
Wikipedia says that an editor who wants to do differently from what a guideline suggests, must give justification for that contravention. I have done so.
…or did you miss that?
Anyone who didn’t know you better might get the impression that you just want to keep favorable information about Gall-Peters out of the article.
Wikipedia, in various of its articles, points out that there are lots of editors who try to use an incorrect literalist misinterpretation and mis-stating of the guidelines, for the purpose of trying to exclude content which they don’t like, or with which they disagree. They say that that is quite common at Wikipedia.
When I visited this article in recent weeks, I read old talk from years ago, and I replied, at this talk-page, to someone who had, long ago, requested a pros/cons section. I said it’s astounding that this article about an unprecedentedly popular projection still has no pros/cons section. I said, “Have we been overzealously editing?”, because it was obvious that something very wrong has been going on, for there to still be no pros/cons section. Want to know why there isn’t one? Look at the most recent talk-page posts.
Evidently this article currently has a set of editors who don’t want a pros/cons section, who don’t want the article to say anything favorable about GP. Evidently the editors who felt otherwise (I’d been reading old talk-page from some years ago) have by now given up & left in disgust. That means that the only I way can enforce a balanced article with a genuine pros/cons section will be by appeal to Wikipedia administration. That will probably be a long procedure, and one that I don’t really want to initiate at this time.
- Oh, and as you've been told before, please sign your contributions.
Ok, I’ll come up with a good pseudonym, and start signing with it in the officially-recommended manner
…maybe “Arno”.
BTW, I emphasizes that much of what I’ve lately posted has been in reply to people who objected to my statement that typically, and especially for wall-maps, a map’s X-dimension is its fit-critical dimension.
Admittedly sometimes there could be circumstances, such as some bookpage-fits, that could make the Y-dimension fit-critical. Maybe, especially for some bookpage applications of single maps on some book-pages, it often isn’t known which dimension will be fit-critical, or maybe sometimes neither one is.
For those instances, then, such things as point-min-scale and av-scale, instead of referencing the width or the equatorial-scale, would have to instead reference the height or the average scale along the central-meridian, or the average scale across the map’s largest Y-extent--or just the area (or its square-root) of the map’s circumscribing-rectangle.
My discussion of av-scale, and my list of av-scale values for various equal-area projections, referenced the equatorial-scale, assuming that the map’s X-dimension is fit-critical. I didn’t do the calculations for the other circumstances, for reasons of brevity.
But I told of a reason why the equatorial-scale seems special: The fact that the geometric-mean- scale on Sinusoidal and Lambert CEA is exactly equal to the scale along the equator.
But, obviously, for those other circumstances, when the map’s Y-dimension or the area of the circumscribing-rectangle is a more appropriate reference-quantity, then one would use it instead.
I emphasizes that this isn’t a “treatise”. I’m just replying to the objections expressed by Strebe & by Justin Kumemuni, about my assumption that a map’s X-dimension is its fit-critical dimension. -- Above comment by User:97.82.109.213
- Yet another badly-formatted wall of text. I'm not going to reply in detail.
- I'll just point out that yes, WP policies are not rigid, but if you want to challenge them, you need to convince other editors... which you're unlikely to do if you question their good faith and ignore their sincere advice. --Macrakis (talk) 21:14, 11 August 2021 (UTC)
This post replies to Strebe & to Justin Kunimune:
Strebe:
In this post I’d like to, 1st, reply better and more clearly to some things that you said about scale;
…and 2nd, to ask you a question. The question is below in this post.
You said:
- With “large” undefined here, I don’t know what that intends to mean. You state, without :evidence, that width is typically the limiting factor for a wall map.
Incorrect. I told why it’s so. I don’t have time to repeat it, and to save space, I won’t.
- I also disagree that wall maps are necessarily what is important.
Our subjective opinions about what’s important have no place at Wikipedia.
But obviously sometimes atlas thematic maps, and sometimes wall-maps, are important.
Obviously GP’s scale-advantgage only exists when width is the fit-critical dimension. Sometimes that condition doesn’t obstain. Therefore sometimes GP doesn’t have that advantage.
Likewise, sometimes GP’s enormous scale-advantage, even when it obtains, isn’t needed. Sometimes larger scale can be useful, sometimes unnecessary.
In summary, sometimes GP’s scale-advantage exists & is useful, and sometimes not.
Hello? It’s well-understood by cartographers that different maps are useful in different applications. GP is no exception. It’s one thing to say that GP, like other maps, is only sometimes advantageous. It’s quite another thing to claim that it doesn’t sometimes have a significant advantage that’s sometimes important. … as do map-projections in general.
• :”Large map-area means more room for more detail, more labeling, &/or larger :labeling.”
- Not so. As an equal-area map, Gall–Peters has exactly as much area as any other equal-:area map.
No, I explicitly referred to area for a given width.
- The massive left-right stretching in the mid- and higher latitudes is negated by increasing :top-bottom compression toward the poles; likewise, the vertical stretching in the low :latitudes is negated by the east-west compression.
Irrelevant. When you everywhere expand a CEA map north-south, you increase, at every point, the scale in every direction other than east-west.
And yes, that’s equally true in the regions with skinny Tissot-ellipses. In fact, that’s where the scale-increase is needed the most.
And I remind you that I explicitly exclude the poles from the points that I’m referring to, because, with most world-maps, at the poles there’s an infinite scale, to which a numerical-value can’t be assigned. • :”And it's obvious that EW expansion, at all latitudes, to the map's full equatorial :width, combined with large NS expansion, must and does increase scale at every :point in every direction.”
- This is not only not obvious; I cannot even tell what you mean. Every map projection :distorts scale. To claim “in every direction” is to claim something apparently false, since :north-south compression on Gall–Peters increases infinitely at the poles such that the :scale in the north-south direction at the pole is zero rather than 1.
Wrong. I explicitly exclude the poles from the points to which I refer.
Equal-area maps have points with low point-min-scale. But a general expansion of the map in the direction of that min-scale will increase it. …and also increase scale in every direction other than the direction perpendicular to the direction of the expansion.
• Large scale allows nearby points to be more easily resolved and distinguished.
- It doesn’t have “large scale” by any meaning I know of.
The geometic-mean, over all of a map’s points, and over all directions at each point, is proportional to the map’s area.
A larger map has larger geometric-mean scale.
…and general overall expansion of an entire map in a particular dimension increases scale, at every point on the map, in every direction other than the direction perpendicular to the expansion.
That’s why, with GP, for all points between lat 60 south and lat 60 north, there is no point at which there’s a direction in which the scale is less than the scale along the equator.
- Severe north-south compression in the high latitudes ensures that points oriented :vertically are less easily resolved (than… what?).
…and a general north-south expansion of the map will increase those compressed scales. That’s a good reason for expanding a CEA map north-south. …a practice that began at least as early as 1870. (Smythe CEA lowered the aspect-ratio to 2, and thereby increased scale, at every non-pole point on the map, in every direction (other than east-west), referenced to the scale along the equator.
And, as I said referring to the fact that expanding a map increases scales on a map. …and, in particular, the fact that a general expansion of a map in a particular dimension increases the scale at every (non-pole )point on the map, in every direction other than the direction perpendicular to the expansion….Those facts are so blatantly-obvious that, by Wikipedia’s rules they do not need citation of a notable or “reliable” source.
As I said, Strebe, this article is very fortunate to have an in-house resident cartographer.
…so that editors can ask you about the validity of statements about maps, and, in particular, about the map that is the subject of the article. Surely you’d agree that it’s good that you’re here to answer such questions.
And so I’m going to ask you two brief, simple & straightforward Yes/No questions.
Like all Yes/No questions, each of these two questions has four possible answers:
1. Yes
2. No
3. I don’t know.
4. I know, but I refuse to say.
Question #1:
Is the following statement true?
With Gall-Peters, between lat 60 south & lat 60 north, there is no point at which there is a direction in which the scale at that point is less than the scale along the equator.
Question #2:
If the answer to the above question is “Yes”, can you name another equal area map projection that has been published, sold, and used by purchasers, and for which the above statement can be correctly said? That’s two Yes/No questions, each of which has the four above-listed possible answers.
I thank you in advance for helping to inform the editors at this article. --------------------------------------------------------------- Justin Kumimune—
I’d like to reply better and more clearly to a few things that you said:
You said:
- While I don't disagree with any of your points factually, I do continue to think that most of them :are trivial or of debatable relevance.
Our personal feelings and opinions have no place at a Wikipedia article. Either a map has some particular advantage under some circumstances, or it doesn’t. Either that advantage can be useful, or not. Period.
- Your point about the Gall-Peters projection's area is true, given the assumptions you have laid :out. But I don't think that width is the only important dimension for a poster.
I make no such claim. GP has a enormous scale-advantages when width is the fit-critical dimension. Those advantages don’t exist if width isn’t the fit-critical dimension. Sometimes it isn’t. We needn’t quibble about how often it isn’t.
And, even when width is the fit-critical dimension, and so GP has its enormous scale advantages, scale might nor might not be important, depending on the application. Is the map only intended for decoration of the wall? Is globe-realism the more important consideration? Maybe one isn’t going to do the precise or distantly-viewed examinations in which scale matters.
In summary, sometimes GP doesn’t have its scale advantages, and sometimes they don’t matter, even if it does have them.
Yes, cartographers have long been familiar with the fact that no map is the best choice for every application, every situation. Different projections are useful in different applications.
As I said, we needn’t quibble about how often GP has its advantage, or how often that advantage is needed. It sometimes has that advantage, and it’s sometimes useful.
- That's why we don't place posters adjacent to corners
You’re saying that we don’t place maps with their sides adjacent to the extreme ends of a wall?
Of course not, for a number of reasons. For one thing, a map that large would be expensive to purchase, and awkward to transport home after purchase, and costly for businesses to ship & store.
For another thing, often there are other things (shelves, posters, portraits, etc.) that one wants to put on a wall. …sometimes including windows.
But, as I said, another thing we don’t do is place a map adjacent to the ceiling or near the floor, and so, since maps & other posted-things aren’t vertically-stacked, there’s no limit on their vertical-extent, and the fit-critical dimension is width.
Anyway, as I said, I don’t claim that width is always fit-critical, or that GP always has its scale-advantage, or that that advantage is always needed. …as is the case with other maps and their advantages.
- , and why posters are usually landscape
- even when they don't have to be.
Lots of posters are oriented vertically too. I don’t know that horizontally-oriented posters are more frequent. But you won’t find wall-maps up by the ceiling or down by the floor. If they must be fitted with eachother, it’s horizontally.
- Furthermore, the efficiency with which a map fills a rectangle does not vary much across :projections. A rectangle can fill a poster or a page with 100% efficiency, and a projection like :Mollweide, which is not space-efficient at all, fills the same with 79% efficiency. That means :that on average, point elements on a rectangular map projection are only 11% farther away :from each other than the same points on a Mollweide projection that fills the same rectangular :area.
It isn’t just a matter of space-efficiency. Aspect-ratio, too, affects av-acale referenced to the scale along the equator (…which I don’t claim is always important).
That’s why, with GP, from lat 60 south to lat 60 north, there’s no point at which there’s any direction in which the scale is less than the scale along the equator.
…and it’s why av-scale (geometric-mean scale, referenced to the scale along the equator), though varying only slightly among most equal-area maps, and remaining very close to unity for nearly all equal-area maps, is enormously larger for GP. …about 1.4 times its value for most other equal-area projections.
And I’ve told why it’s blatantly obvious to anyone that GP’s greatly multiplied tallnesss will greatly increase scales on the map. …scale at every point on the map, in every direction other than east-west.
That’s far, far too obvious to need “citation of a notable or reliable source”.
As I said, GP’s scale advantages are enormous when they obtain (and they sometimes do). And they’re sometimes useful.
…which is as much as can be said for other maps & their advantages.
:I think that's too small to mention.
See above.
- To state my personal opinion, I don't think the Gall-Peters :projection has any redeeming :qualities for any purpose when compared to other equal-area projections.
See above. And remember that personal opinions have no place at Wikipedia.
- More to the point, I think reliable sources omit these things because they view them as minor :or irrelevant, not because they are too obvious.
Anyone’s personal subjective views have no place at Wikipedia. …and that includes unsupported opinions about the views of notable authors.
- I think I understand the crux of this disagreement. You are arguing that these pros are sometimes relevant, while others have been arguing for they are not usually relevant. Those aren't directly contradictory, so we've been talking past each other somewhat. It's important to note here that just because something is sometimes useful doesn't mean it merits inclusion in an article.
- This is because your list is not exhaustive and never can be. If we try to think of every pro that could ever be relevant without considering how relevant it is, we will produce a list hundreds long, and most of it will be useless. For instance, we will note that its grid-shaped graticule works well for custom Sid Meier's Civilization IV maps, and that it makes the island of Cuba fit neatly in a golden rectangle. On the con side, we will note that the small aspect ratio is bad for situations where height is the limiting dimension, or where it has to fit on a widescreen TV, or a computer monitor, and that the dash in its common name makes it difficult to encode in some contexts. These points are true, and relevant to some contexts, but it would be silly to include all of them in the article.
- That's why editors must exercise judgement to decide what information to include (usually using the RSs as a guide), as specified in WP:INDISCRIMINATE, and elaborated on in this explanatory supplement.
- If you wish, we can discuss the importance of each of these pros in our own opinions (there's no rule against that unless it violates specific policies). But I agree that it would be better to use an objective metric for what merits inclusion. "It is true and sometimes useful" is not a sufficient metric, as it would make articles unreadably long, so in lieu of that, the simplest and most common metric is "it is included in the RSs" (though even this sometimes includes too much information). Only four pros of this projection are published in reliable sources as far as I can find (listed above). I don't see any reason not to include those, but most of the points you mention are, going off of their absence in sources like J.P. Snyder's Album of Map Projections and M. Monmonier's Rhumb Lines and Map Wars, excessive detail. Justin Kunimune (talk) 03:02, 14 August 2021 (UTC)
First, of course it can’t be denied that GP has a significant disadvantage: It looks awful. …unrealistic & ugly, an affront to aesthetics. We all know how Robinson described it. It looks as if Africa & South-America were made of wax, and someone forgot to turn on the air-conditioner.
As an admirer of the Mercator’s accurate local portrayal and mapping of each place, I have to say that GP doesn’t portray a good picture of tropical places. ….so FUBAR as to maybe sometimes be inconvenient to use.
Yes inconvenient, but usable, as a practical-matter, for a working-map …and, if unappealing & even maybe sometimes inconvenient, that’s a trade for the potentially bigger scale that will sometimes make the map usable at all, making usability at an otherwise unusable distance.
Yes, its main advantage, scale, sometimes exists & sometimes doesn’t. ]
The disagreement is as you described: The advantage sometimes exists, vs the advantage usually doesn’t exist.
To me, the latter sounds like something that would best be said only if the advantage can be shown to be vanishingly unlikely. …otherwise it’s just a matter of wording-choice or individual subjective impression.
Because one doesn’t want a map up by the ceiling or down by the floor, then there isn’t vertical room to vertically-stack wall-maps, and so, if they’re fitted together, it’s horizontally…making width the usual fit-critical dimension for wall-maps.
Schoolroom maps are usually wall-maps. That’s surely what the Boston school-system’s decision was about. That wall-map is typically viewed at a distance, at least partly across the room, from students’ desks.
Sometimes short distances matter a lot, when it’s a matter of where a point is with respect to a national-border or a thematic-map’s isopleth or zone-boundary. For such precise determinations, at an across-the-room distance, scale can matter a lot.
Therefore I claim that GP’s scale advantage usually exists and matters for classroom wall-maps.
About GP, maybe school-kids who like scary-movies would like it, and might call it “That Wax-Museum Map”.
Another thing: It’s likely that the deformation of Africa & South-America was what provided visual psychological confirmation to people that something different was being done, that Africa was indeed shown big. The deformation dramatized & proved the bigness!
Maybe that’s why (it seems to me) Peters once said that the other maps called “equal-area” aren’t really. Maybe he, and many others, thought that nothing is changed unless it’s visible as that great 1-dimensional distance-multiplication.
So maybe the deformation is why equal-area maps are in use by lots of socially-conscious organizations and by British & Massachusetts schools.
I listed a number of other advantages that GP has in common with other cylindrical projections. They’re arguably obvious. Cylindrical projections’ equal portrayal of all longitudes is a well-known advantage. Surely it’s better if a school-map doesn’t disfavor some longitues.
I suggest that, given the choices of for-sale maps available to it, the Boston school system made a good choice, arguably the best choice.
Would I use GP? No, I’d use CEA-Stack instead. …and Behrmann where CEA-Stack’s great scale & high-lat shape advantages aren’t needed, or where CEA-Stack wouldn’t fit vertically.
This is just a quick preliminary-note.
To be continued…
BTW, to give credit where due, GP could easily be mistaken for the work of Salvador Dali, which surely counts favorably.
So I take back what I said about GP being “…ugly, an affront to aesthetics”.
How come it’s ugly when James Gall does it, but when Salvador Dali does it it’s worth a million dollars?
But I don’t retract “unrealistic”. It’s an undeniable gross misportrayal. …justified for highschool geography classes, when precise distantly-viewed observation, estimate or examination of exact relative positions makes good scale paramount and, to that end, justifies bad shape-portrayal.
…but not for elementary-school classes intended to give students a good idea of what the Earth looks like.
For that purpose, Behrmann & Mollweide would be much preferable. I agree that it doesn’t have to be just one projection. …Mollweide for its globe-realism (interrupted on only one meridian, or on two meridians and shown as two realistic circular views of the Earth). …and Behrmann for its equal portrayal of all longitudes.
In elementary-schools, Apianus II & Plate-Carree could be introduced, to establish the realistic circular Earth-view, the horizontally-doubled circle to show all, both sides, of the Earth; and the natural rectangular grid of cylindrical maps…and the grid-plan intention. …and then it could be explained that, to show all places in correct area-proportion, those two projections’ parallels can be adjusted, resulting in Mollweide & Behrmann, which would be on the wall.
At a somewhat later grade, the geometric explanation for Behrmann could be graphically-explained, and even that of Mollweide could (maybe a bit later) be explained too. But it should be emphasized to the listener that it isn’t necessary to follow (& be able to repeat) that geometric derivation. Merely seeing it done, observing the rough gist of it, shows that there is such an explanation, & that the person would be able to understand if they studied it.
It’s enough that each part of the explanation is plausible.
I claim that maps’ construction & properties should be explainable in that way, to anyone & everyone. That’s one of the things that I like about CEA. …and it’s why I claim that Equal-Earth is inadequate.
Sinusoidal? It’s the simplest constructed & explained, but it’s also a terrible portrayal of shapes over much of the Earth, not useful either for distantly-viewed precise relative- position observation, or for elementary-school portrayal of how the Earth looks.
But, after introduction of Apianus II & Plate Caree, followed by an explanation of their inexact area-proportions, why not show the obvious natural way to achieve right-area-proportions. …by drawing the parallels with their globe-true length, and their globe-true spacing?...and then point out that the same accurate area-proportion can also be be achieved by adjusting the parallels-spacing of Apianus II & Plate Caree. …which gives better general shapes & better overall size & scale.
Maybe some kids wouldn’t care, but, for those who did, their questions about what is done and why would be answered.
But just to clarify something: I'd substitute CEA-Stack for GP, for all the applications that I said that GP is good for...and for Many others too*, because CEA-Stack shows much better shapes at all latitudes, compared to GP.
- i.e. Whenever best-realism or 1-map-simplicity isn't needed, and
very good scale & shape are desirable.
Yet another wall of text. Please remember that "Talk pages are for discussing the article, not for general conversation about the article's subject (much less other subjects). Keep discussions focused on how to improve the article." WP:TALK#USE These long contributions aren't helping. --Macrakis (talk) 21:49, 15 August 2021 (UTC)
Most of what I said was directly relevant to the things I suggest saying in the article, and the objections to those things.
The criticisms of GP, of varying merit, are certainly relevant, because those are issues about what can be said in the article.
And, in an article about GP, when editors are cl aiming that GP is meritless compared to the other equal-area maps, and where I'm defending the merit of GP at this talk-page, it's reasonable for me to admit that yes, GP is completely merit-dominated(by CEA-Stack) .
If GP genuinely isn't really the best for any application (because it's completely merit-dominated by CEA-Stack), then it shouldn't be taboo to say so...at the talk-page, and yes, even in the article.
In response to
- To me, the latter sounds like something that would best be said only if the advantage can be shown to be vanishingly unlikely. …otherwise it’s just a matter of wording-choice or individual subjective impression.
It doesn't need to be shown to be vanishingly unlikely. Standard practice is to only include facts if they are present in the RSs – that's WP:VERIFIABILITY (just so we're all on the same page: "verifiability" in the context of Wikipedia means that a fact can be found in a RS. Editors like Strebe are not themselves RSs, so having him confirm something does not make it WP:VERIFIABLE). Encyclopedic sources like Flattening the Earth and An Album of Map Projections don't mention things like aspect ratio or av-scale, so these facts aren't WP:VERIFIABLE even if they are verifiable in the colloquial sense. In addition, facts are usually only included if they are relevant to the subject's notability. The cartographers who use GP and the activists who write about it today only cite its cylindrical and equal-area properties, so the other pros listed above are not relevant to its notablity. As you have pointed out, such guidelines can be suspended in exceptional cases, but I don't see that there is sufficient reason to do so here, given how long the article will become if we include all pros that are sometimes relevant.
In response to the specific point about the aspect ratio and width: You can see from this picture of a poster in a Boston classroom that there is ample space both on the sides and on the top and bottom.
If they wanted to get a different equal-area projection with a larger aspect ratio, they could easily get one with the same scale and still have horizontal space to spare. They would have to move "oceans", "Peters Projection", "equator", and "hemisphere" to above or below the map, but "landforms" and "scale" are already there, so that shouldn't impact the display's readability. Based on how people use and talk about world map posters, it seems to me that the determining dimension of a poster is not its width but its total area, as that determines how much space it takes up visually and, as you noted, how expensive and awkward to transport it is.
Justin Kunimune (talk) 03:11, 20 August 2021 (UTC)
Justin—
As I said, often an advantage of a map only obtains under certain conditions and applications. That’s as true of GP as it is of maps in general. No map is best for all applications.
You can’t use a WP policy as a reason to say that there can’t or shouldn’t be an exception to that policy…unless you can show that that exception would be detrimental to the article and its informing of readers.
I’ve told why an exception to the policy is needed, and would improve the article. …the exception of allowing a pros/cons section even though GP’s advantages & disadvantages don’t have notable citations. A complete pros/cons section is nonetheless needed. The articles’ readers would be informed much better, and the article would indeed be (much) improved.
Additionally, WP explains that verifiability (by its usual meaning in English) is the reason why notable citations are ordinarily required. But this isn’t an ordinary circumstance, due to the presence, at this article, of a cartographer who is considered, by the other cartographers, to be reliable.
It’s obviously a matter of legalistic-ness vs common-sense. If the numerical facts in my proposed section could easily be verified or refuted, by that agreed-reliable cartographer, then it’s verifiable, in any meaningful sense of that word.
So, by common sense, if the information would improve the article’s informing of readers, and is verifiable, then how would you claim that it would be detrimental to the article?
Yes, a listing of the GP advantages & disadvantages I stated—having a genuine pros/cons section--would inevitably lengthen the article…by one section. …a necessary section.
If you’re concerned about article-length, then delete the long, unnecessary & irrelevant material about scandal-history.
As I said, it’s common and typical for maps’ advantages to only obtain in some circumstances & applications. If, as is indeed sometimes the case, a world map on a wall doesn’t have to compete at all for wall-space, then, yes, space-efficiency would replace width as the limiting quantity. …as you said, because the mapsheet-area affects expense. …and because a map extending to floor & ceiling would have visibility problems near the floor, and be seen at an unhelpful angle near the ceiling, for close-seated students. …and the left & or right ends of a whole-wall-covering map might be seen at an unhelpful angle for some close-seated students. Those are drawbacks for a whole-wall-covering map.
When there’s no space-competition, obviously Behrmann would be, scalewise, as good as GP…and has better shape over more of the Earth. Likewise, to a somewhat lesser degree, for Eckert IV & Equal-Earth. …and for Mollweide, to a slightly lesser extent.
(…but Equal-Earth still suffers from a big uniquely-difficult-explanation disadvantage.)D
Disadvantage of GP:
What is GP’s problem? It’s obvious at a glance. As a greatly NS-Expanded CEA map, GP obviously gives good European shapes—Its standard-parallel is at lat 45.
Equally obviously (even moreso, actually), as a greatly NS-Expanded CEA map, GP has drastically-unrealistic shape in the tropics.
Those statements don’t require Original-Research, or citation of a Notable journal. :D
So, without any Original-Reaserch, it’s plain that a greatly NS-expanded CEA map is great for higher latitudes, and no good for low latitudes. No Original Research there.
Given the above, then where would it be good to use a greatly NS-Expanded CEA map?
Let me guess:
…at high lat, and not at low-lat?
That, too, doesn’t require Original-Research, or a citation of a peer-reviewed journal :D
But that’s just a description of CEA-Stack’s high-lat map-sections.
CEA-Stack automatically, inevitably, comes up when GP’s problem is mentioned…as described above.
…and therefore isn’t off-topic in a GP pros/cons section -- unsigned comment by User:97.82.109.213 at 2021-08-26T14:01:37
- Again, please sign your comments and use standard wikipedia formatting! --Macrakis (talk) 20:40, 26 August 2021 (UTC)
It would be more productive if, instead of adding more text to the Talk page, you added one important and well-documented advantage to the page itself, with sources. You seem to consider its aspect ratio to be an advantage. Fine. Add something like this:
- The Gall-Peters projection is popular among elementary-school teachers because at a given height, it is narrower than other equal-area projections.[1]
- ^ Journa List, "Survey shows teachers like narrow maps", Chronicle of Lower Education 43:7:321 (July 2021)
or even
- Some cartographers praise the narrow aspect ratio of Gall-Peters, saying that it fits walls better.[1]
- ^ Re Porter, "ASC passes Gall-Peters Resolution", Cartography Today 22:1:123 (January 2020)
Now, I suspect that you won't be able to find reliable sources like this, which means that the claim is based on your own reasoning, what we call here original research. But if you do, knock yourself out. I see no reason for a derogation from our usual rules, which are designed precisely for cases like this. --Macrakis (talk) 20:40, 26 August 2021 (UTC)
Just briefly:
I'd quote such references if i'd found any. As you suggested, there don't seem to be any.
Incorrect. WP says that facts obvious to everyone are NOT "Original-Research", and therefore aren't prohibited from WP articles.
By the way, I didn't list aspect-ratio as an advantage. I listed large point-min/max-scale and point-min-scale--and high values for them over a large percentage of the Earth--as advantages.
We've already been over this:
It doesn't take a journal-article to establish that a map is more usable from across the room if scale is larger. Must I quote an educational journal to establish that readability is better than non-readability? :D
Nor is there any shortage of available citations (need I cite them?) that people object to the bad shape that results from low point-min/max-scale.
Yes, low aspect-ratio favors a map's rating by global measures of point-min-scale--referenced to the scale along the equator (as it is, as I define it for cylindrical or pseudocylindrical maps).
And yes, low aspect-ratio favors a map's rating by av-scale, which I defined with reference to the scale along the equator.
I acknowledged that maps & other posted things don't always have width as their fit-critical dimension(Maps often don't have their advantages in all applications.), and that GP's advantages that depend on width being fit-critical don't always obtain.
However, posted things, and maps especially, are always posted at a height not close to floor or ceiling...and therefore would compete with eachother for horizontal-space at that middle height. ...if there are enough of them on the wall to compete, as admittedly there aren't always.
But I didn't list low aspect-ratio, for its own sake, as an advantage.
User:97.82.109.213 at 2021-08-27T03:25
edited 03:54
You aren't advancing the discussion. I was suggesting a productive way forward -- start with one claim (aspect ratio was just an example) and write it up with proper reliable sources. See also WP:STICK and WP:IDHT. --Macrakis (talk) 15:24, 27 August 2021 (UTC)
Sorry, but the answers to your objections don't change when you repeat the objections. So yes I repeated the answers. But yes, it shouldn't have been necessary to do so.
User:97.82.109.213 at 2021-8-27T22:12
Oh, one other thing I should mention:
I pointed out that the OR rule, by its own wording, doesn’t apply to things obvious to everyone, and I suggested an exception to the verification by RS rule, and told how I justify the exception. I told why it would improve the article.
I asked for reasons why the exception, in this instance, would be detrimental to the article.\
The answers that I got consisted of repetition of the policy to which I’d suggested an exception. No, as I’ve already pointed out, the policy itself can’t be used as a reason why it can’t or shouldn’t have an exception.
But if you don’t have a reason why the exception would be detrimental to the article, I don’t care.
The fact that you didn’t give a reason when asked for one will be helpful when I later take the matter to Wikipedia administration.
Given the current ideological-POV demographic-composition among the editors at this article, it’ obvious that the GP article will never have balance or objectivity, or a pros/cons section, without the help of administrative enforcement.
As I’ve said, that would probably be a lengthy process--a project that it isn’t possible for me to embark on just yet. User:97.82.109.213 at 2021-8-29T22:12
- The fact that there are objections among other editors here on this Talk page is sufficient to show that what you want to say isn't "common knowledge".
- You also don't seem to understand the role of Wikipedia administrators.
- As I have said before, I recommend that you learn more about Wikipedia conventions and procedures (starting with how to write Talk page comments) before continuing. --Macrakis (talk) 23:02, 29 August 2021 (UTC)
This comment is relevant to the article, because it’s something that should be in the article, in the Disadvantages section (…if there were one, as there should be.)
Yes, GP, at is equator, has a point-min/max-scale of only .5
But, you know, it’s common for equal-area maps to have point-min/max-scale as low as .5 or lower at some place on the map.
So, as a practical matter, yes GP might be inconvenient to use where the point-min/max-scale is so low. But likewise on other equal-area maps that have a point-min/max-scale that low somewhere.
Yes, what people object to about GP is that its low point-min/max-scale occurs at in the tropics, and, in particular, even at the center of the map. That makes the resulting unrealism much more blatant and in-your-face. That’s why some people don’t like GP.
An answer to that: Realism isn’t everything. If you want it to really look like the Earth, then put on your wall a photo of the Earth from space. A map is intended to map the Earth, not impersonate it.
And if you find GP unaesthetic, then remember Salvador Dali.
Maybe GP’s name should be changed to the Salvador Dali Projection.
Relevant to GP's advantage:
GP can only be recommended for a special situation: A wall that's crowded, with competition for horizontal-space, or soon will be; a need for accurate measurements or examination of relative-position, or distant-examination; a requirement to use only maps currently for sale (i.e. CEA-Stack not available). Without those conditions, of course Behrmann would be much better than GP, due to its good shape over 2/3 of the Earth's surface.
In fact, for a horizontally-crowded wall, a twice-interrupted world-map, with 2 separate maps, each mapping half of the Earth's longitude, with the two maps mounted one over the other, would beat a one-piece GP map, by geometric-mean scale for a given width, no matter which equal-area projection is used.
For example, a twice-interrupted, vertically-arranged, Behrmann or Sinusoidal world-map would beat a 1-piece GP map, by geometric-mean-scale for a given width.
And of course it goes without saying that the twice-interruption would reduce Sinusoidal's peripheral distortion. — Preceding unsigned comment added by 97.82.109.213 (talk • contribs) 20:29, September 4, 2021 (UTC)
- Please sign your talk page posts. Use ~~~~ to generate a timestamped signature. Meters (talk) 20:52, 4 September 2021 (UTC)
- You might want to read WP:TLDR. You have been given some good advice. Try following it. Meters (talk) 20:56, 4 September 2021 (UTC)
I took some of the advice (e.g. signing posts; methods for quoting, etc.)
Not all of the advice was consistent with actual Wikipedia policy...&/or previous practice at this talk-page.
I'd been signing my posts, with a date & time. Yes, I forgot to do so on my most recent post before your comment.
User:97.82.109.213 at 2021-9-6T0018
New Comments on January 12th, 2022:
Wikipedia’s guidelines are only meant as suggestions, not as exceptionless rules. Wikipedia emphasizes that common-sense can call for an exception to a policy. …and Wikipedia acknowledges that some Wikipedia editors misinterpret policies as excpetionless rules in order to prevent the inclusion of material that they personally dislike. …as is the case here, when we have people trying to claim that Gall-Peters’ advantages can’t be mentioned in the article (making it impossible to have a pros/cons section), because “reliable sources” don’t talk about Gall-Peters’ advantages (…and the resident cartographer here refuses to answer a simple straightforward Y/N question about one of the advantages).
Well, I’ve asked a cartographer here, at this article talk-page, the following question:
“Is it or is it not true that, on Gall-Peters, nowhere between lat 60 north & lat 60 south, is the scale at any point, in any direction, less than the scale along the equator & on the reference-globe or generating-globe?”
Yes or no. It’s a simple enough question, and not one that should be a problem for any genuine cartographer.
And yet the resident cartographer at this article refused to answer the question.
Not only does our resident cartographer here refuse to say that it’s so. He refuses to say that it isn’t so. Is that because it’s unknown or unknowable ? :-D No, it’s a straightforward y/n question easily-determinable matter
BTW, the region between lat 60 N & 60 S comprises about 86.6 % of the Earth’s surface.
So here’s another question or our resident cartographer:
What other equal-area world-map has scale at least as great as the scale on the map’s equator & reference-globe, everywhere, in every direction, over 86.6% of the Earth’s surface?
(…other than other CEA maps such as Balthasart, Square Tober CEA, & CEA-Stack.)
Does anyone really believe that a refusal to answer those questions will successfully keep that GP advantage out of the article, when the matter is appealed to Wikipedia administration?
BTW, CEA-Stack completely dominates GP. On CEA-Stack, with its Behrmann main-map, and with three added northern high-lat sections, CEA-Stack shows about 99% of the north-of-the equator part of the Earth with scale, in every direction at every point, at least equal to the scale along the equator.
…and shows about 95% of the north-half of the Earth with “good shape”, by which I mean point-min/max scale of at least ¾ (That’s the point-min/max scale at Behrmann’s equator).
…and that CEA-Stack version accomplishes all that, with an aspect ratio that’s a near-perfect fit to an 8.5X11 sheet of computer-paper.
GP has good shape over only 21.3 % of the Earth’s surface.
(The high-lat sections wouldn’t be needed in the South, where even the first one would be needed by only a small amount of land at the tip of South-America. (…unless one is very interested in Antarctica.) Of course, if desired, one high-lat section could be added in the South, for good scale & shape even in that tip of South-America…the Southernmost inhabited continental land.)
BTW, even ordinary Behrmann CEA easily beats Equal-Earth, with good-shape, over 2/3 of the Earth’s surface.
…& with point-min-scale at least equal to scale along equator, over 2/3 of the Earth’s surface.
User:97.82.109.213 at 2021-1-12T12:55 — Preceding unsigned comment added by 96.39.179.76 (talk) 09:55, 12 January 2022 (UTC)
- we're not misinterpreting policies as exceptionless rules. we're using the policies as they are intended: to prevent common mistakes from degrading the quality of articles. in this case, the mistake would be cluttering it with unimportant unsourced criteria. this would make the article either very long (if we simply listed every possible pro or con we could think of) or very POV (if we subjectively choose to include only the few that we find important).
- your criterion about the fraction of the map within which nowhere "is the scale at any point, in any direction, less than the scale along the equator" is not important. this is a highly specific set of words that does not correspond to accuracy. the GP projection has an abnormally small scale along its equator, so naturally most of its linear scales are greater than that. that doesn't mean that 86.6% of the surface has "great scale"; that means the equator has such bad scale that only 13.4% of the map is more distorted than it.
- your point about it fitting on a 8.5"×11" sheet of paper is unimportant. most people who put maps in books are used to dealing with diagrams whose aspect rations don't match the page. they usually add interesting information in the gap. if this were a real concern for cartographers or publishers, it would be mentioned in a reliable source.
- your criterion about the point-min/max scale is actually important, and I think I've seen it in some reliable sources. [a] comes to mind. I thaut I saw someone create a new map projection based on this, but I can't remember the details. if you want to add a sentence or two about this point, I wouldn't argue, tho we'll want to make sure we list a few different distortion criteria, as there are many used in the literature (see [b]).
- I think a short pros/cons section is fine, but to keep the number of items manageable in an unbiased way, it will have to be based on RS. I've pointed out a handful of sourced pros for the GP projection. anything else is probably not important enough to readers or cartographers to include.
- [a] Yan, Jin & Xu, Tiansheng & Li, Ni & Gong, Guanghong. (2021). Regression and Evaluation on a Forward Interpolated Version of the Great Circle Arcs–Based Distortion Metric of Map Projections. ISPRS International Journal of Geo-Information. 10. 649. 10.3390/ijgi10100649.
- [b] Kerkovits Krisztián (2019) Comparing finite and infinitesimal map distortion measures, International Journal of Cartography, 5:1, 3-22, DOI: 10.1080/23729333.2018.1500255
- 96.39.179.76 wrote: Not only does our resident cartographer here refuse to say that it’s so. He refuses to say that it isn’t so. Is that because it’s unknown or unknowable ? The answer is neither. The answer is because the question is irrelevant. Wikipedia, including its talk pages, is not a forum. If something is important enough to be in Wikipedia, it’s important enough to be found in reliable sources. That’s the solution to your editing problems: Find it published or get it published—in a source that meets the reliability requirements of Wikipedia. Strebe (talk) 22:00, 12 January 2022 (UTC)
First just a quick comment:
How very bizarre, to claim that point-min-scale doesn't matter. Look at high-lat peripheral places on Sinusoidal, or at the top of any line-pole equal-area map, and say that :-D.
In a classroom, it's often necessary to observe a map from a distance, because not all of the seats in the room can be close to the map. The distance at which a short map-distance can be discerned or compared is proportional to the map's scale at the point & direction of interest.
If scale didn't matter, there'd be no reason for atlases to typically use a very large format, compared to other books. There'd be no reason for wall-maps to be roughly 3'X4' instead of postcard-size.
Why equator-length & scale are a meaningful reference:
On many or most Cylindroid (Cylindrical or Pseudocylindrical) maps, the scale along the equator is equal to the scale on the surface of the reference-globe, the generating-globe.
(Yes, the CEA maps other than Lambert are often spoken of as being on a cylinder that intersects the reference-globe. But the non-Lambert CEA maps can also fairly be regarded as just vertically-magnified Lambert maps, sharing Lambert's reference/generating globe.)
Scale-factor on a map is, by its definition, referenced to the scale on the reference or generating globe.
Additionally, as you'll find nearly any time when there's space-competition on a wall, it's the horizontal-space that's in short supply. That makes the equator-length & scale the most useful length & scale reference.
User:97.82.109.213 at 2021-1-12T0042 — Preceding unsigned comment added by 96.39.179.76 (talk) 00:42, 13 January 2022 (UTC)
I compared the aspect-ratio of a certain version of CEA-Stack to that of an 8.5X11 inch sheet of computer-paper, not because I advocate printing maps only on 8.5X11 sheets, but rather as a way of telling the shape of the map, its aspect-ratio. That (11/8.5) aspect-ratio is a convenient and not very atypical shape for a wall-map or book-page.
I wanted to emphasize that the powerful properties-improvements achieved by CEA-Stavk don[t require an unreasonably or particularly unusually tall map. — Preceding unsigned comment added by 96.39.179.76 (talk) 01:10, 13 January 2022 (UTC)
we could argue indefinitely about whether these criteria are meaningful, but I'm starting to realize it's not productive. why don't we try to compromise by adding a paragraph about GP's pros that are based on RS? I would propose something like the following, added to the bottom of the "Cartographic Reception" section.
As of 2022, the Oxford Cartographers website promotes the Gall–Peters projection as "the most accurate possible portrayal of [everyone’s] place in the world". It cites the fact that it shows all areas correctly, the fact that all lines of longitude run vertically, and the fact that all lines of latitude run horizontally as the Gall–Peters projection’s key positive characteristics."[1]
Justin Kunimune (talk) 13:39, 13 January 2022 (UTC)
- Those* are all true, but Oxford Cartographers is not a reliable source. They are a business and an advocacy.
- *The facts, not the claim. Strebe (talk) 18:13, 13 January 2022 (UTC)
[quote] we could argue indefinitely about whether these criteria are meaningful, but I'm starting to realize it's not productive. [/quote]
You got that right. The matter of what’s “meaningful” is a subjective matter of opinion & personal-feeling. There are no RSs on subjective matters of opinion or personal-feeling.
Cartographers, and the publications that publish them, are reliable when stating objective, verifiable mathematical facts.
Cartographers, & the publications that publish then, are reliable when stating their personal subjective opinions, personal feelings, & POV.
Cartographers, & the publications that publish them, are not reliable regarding subjective matters such as their opinion regarding what others should consider important (…but they can reliably tell us mathematical facts that might influence people’s perception of importance.)
When you call certain publications “Reliable-Source”, regarding subjective judgments of importance, that’s nonsense, and it just elevates some group’s POV to governing-status.
So, how can Wikipedia say anything about such matter? Easy. Without calling it a debate (because it wouldn’t be an ongoing conversation in the article), in any instance with two sizable groups ( such as people who like GP, & people who don’t like GP), then just let each of those 2 groups state why they consider GP’s advantages or disadvantages to be. …& how they support their claims about importance.
I’m not claiming that point-min-scale, referenced to map-width, is always important. But it’s important when map-width is the fit-critical dimension. …as it undeniably sometimes is. …and as it usually is in wall-mounting, when fit & crowding is a problem.
If Strebe wants to claim that point-min-scale is irrelevant, then I invite him to share with us why he believes that.
I’ve told why I claim that point-min-scale matters.
If & when Strebe feels ready to, he should be permitted to say why he thinks that point-min-scale is irrelevant, or in what way my argument that it’s relevant is incorrect.
Sorry, but that’s the best that you can do on a fundamentally subjective matter. You can tell about the mathematics, but the importance-judgment comes down to subjective opinion…for which reasons can and should be given.
Now hear this: Don’t use GP when map-height is the fit-critical dimension! Behrmann, or maybe even Lambert, would be better then.
When there’ll likely be crowding, but it isn’t clear which dimension will be more fit-critical than the other, or it’s known that neither will be more fit-critical than the other, then of course space-efficiency is what matters, regarding the matter of av-scale, point-min-scales, or room for map-detail & labeling.
When that doesn’t even matter, because the map will be on a large bare wall with no space-competition, and you can make the map as big as you want, to make any place’s point-min-scale as large as you want, regardless of the projection…then, obviously, shapes, point-min/max-scale, becomes what matters. Behrmann does excellently, with point-min/max scale >= 3/4 , over about 2/3 of the Earth’s surface.
GP’s inaccurate tropical shapes are unrealistic & inconvenient, and, to some, aesthetically-disturbing.
…but not use-prohibitive.
Looking at the equator? Then I remind you that shapes there are really only half as NS-tall as they’re shown. ...as regards the ratio between NS dimension & EW dimension.
Looking at the top or bottom of Africa? Then I remind you that the shapes there are only about 2/3 as NS-tall as they appear. ...as regards the ratio between NS dimension & EW dimension.
Insufficient point-min-scale for precise measurements or viewing at a distance can be use-prohibitive.
GP excels at good point-min-scale, having good point-min-scale over the inhabited latitudes. …out to lat +/- 60. That’s 86.6% of the Earth’s surface, out to the approximate latitude of Oslo, Stockholm & Helsinki.
I define “good point-min-scale” as point-min-scale >= the scale along the map’s equator.
I’ve told why that’s often, though not always, important.
Very often, an advantage only sometimes obtains, depending on conditions. It’s nonetheless an advantage.
Oh yes, & there’s the matter of the reliability of mathematical facts that are stated. Well, anyone can challenge the accuracy of a fact. And no, that isn’t prohibitively time-consuming. It’s common practice everywhere but here.
It isn’t complicated: Someone states a fact. Maybe (or maybe not) someone else challenges it…either by asking for verification, or telling why it isn’t true. Of course merely proving that there’s a consensus among reliably-credentialed people, that it isn’t so is sufficient to refute an alleged objective mathematical fact.
e.g. Strebe could tell us why he believes that GP doesn’t have point-min-scale >= the scale along the equator, between lat -60 & lat +60. …or point to an expert-consensus that GP’s lat-range of good scale is less than that.
That’s how the accuracy of an objective mathematical fact can be verified or refuted.
96.39.179.76 at 2022-1-15 at 0149 UT — Preceding unsigned comment added by 96.39.179.76 (talk) 01:48, 15 January 2022 (UTC)
- As I said more than four months ago
Please sign your talk page posts. Use ~~~~ to generate a timestamped signature.
andYou might want to read WP:TLDR. You have been given some good advice. Try following it.
This talk page thread is now three times as long as the entire article.Meters (talk) 03:33, 15 January 2022 (UTC)
"Reliable source" does not mean "cartographer". RSs include respected peer-reviewed papers, news articles from established outlets, and published books. And RSs are reliable when stating what is important enough to mention. Using RSs this way does elevate some groups' POV to governing status, but that's how Wikipedia is supposed to work. Someone's POV needs to decide what is relevant and what isn't. It could conceivably come from a sizeable group of people selected to represent two sides of an argument, as you propose. But the creators and maintainers of Wikipedia have decided follow RSs.
If Wikipedia was a scientific journal or a news agency, then of course that would be insufficient. We would have to verify all facts, weigh opinions by how well-supported they are, and adjust the narrative to represent all sides fairly. However, while journals and news agencies do exist, Wikipedia is not one of them. Wikipedia is a way for people to access published information in one place for free.
If you think it would be better to gather a sizable group of people, ask them what they think is good about the Gall Peters Projection and why, and list the pros and cons that they identify, then I encourage you to do so and publish the result as a paper or news article or book. If you want more people to know that they should use GP when the width is the fit-critical dimension, then start a blog about map projections and post it there. But until they are published in an RS, these things do not belong on a Wikipedia article.
Justin Kunimune (talk) 15:49, 15 January 2022 (UTC)
Justin--
we've been over this. There are facts that are far too blatantly, ridiculously obvious to require a citation.
96.39.179.76 at 2022-1-15T2305 — Preceding unsigned comment added by 96.39.179.76 (talk) 23:04, 15 January 2022 (UTC)
Meters--
In case you haven't noticed, I've been signing nearly all of my posts.
I tried the tildes. They don't work for me. I don't know or care why. I had a registration here, & have been told that I must still have one. I've tried to sign with it, via the tildes. But, since that doesn't work, I've been signing via my ISP.
You want brevity? Then delete, from the article, all of the entirely-irrelevant material about about cartographer's emotional reaction to Arno, & about Arno's claims, etc. Arno Peters wasn't the introducer of GP, and all that material about him & what he said, & cartographers' reaction to him bears no relation whatsoever to James Gall's CEA version.
All that Arno material could & should be moved the the Wikipedia article about Arno Peters.
The GP article should be only about GP as a map-projection. 96.39.179.76 (talk) 23:15, 15 January 2022 (UTC)
- I have no idea what you mean by the tildes "don't work" for you. Obviously you are using them, at least some of the time, and they are working.
- So, after five months and almost 135 k of talk page discussion you've dropped your idea of adding a section on properties, advantages and disadvantages? OK, well then I suggest that you start a new talk page section to discuss what you now suggest we remove from the article. Meters (talk) 23:35, 15 January 2022 (UTC)
[quote] So, after five months and almost 135 k of talk page discussion you've dropped your idea of adding a section on properties, advantages and disadvantages? [/quote]
No. I said no such thing.
But obviously any progress in that matter will depend on taking the matter to Wikipedia administration, and it might be a while before I have time to give the amount of time it deserves, to that--likely lengthy-- project.
[quote] OK, well then I suggest that you start a new talk page section to discuss what you now suggest we remove from the article. [/quote]
Yes, that calls for a separate section. Getting the projection-irrelevant material our of the article...and moving it to the Arno Peters Wikipedia article.
- With respect to the proposal to add the long pros and cons section (I agree that removing material should be discussed in a separate section for clarity's sake): No one is questioning the truth of these claims. But even if something is uncited, it still needs to be verifiable. Justin Kunimune (talk) 13:56, 19 January 2022 (UTC)
My claims are verifiable, by asking any cartographer (..or, rather any cartographer who is willing to answer :-)
Anyway, Wikipedia is explicit about not requiring verification for things that are obvious.
Additionally, relevance is often a subjective individual matter, and there's no such thing as an RS on a subjective matter. Strebe says that point-min-scale is irrelevant. Why? He isn't saying! :-)
"Relevant" needn't mean "Important & necessary in every instance."
For relevance, it's sufficient that there are non-rare instance in which the fact is useful.
It's just blatantly, ridiculously, undeniably obvious that there are instances in which point-min-scale matters.
What about the fact that there could be instance in which map-width isn't the fit-critical dimension. Again, the extent or size of the region of good point-min-scale,referenced to map-width, is only important when width is the critical dimension. But that's sometimes the case, which is enough for the extent of size of the region of good point-min-scale to be relevant.
And, BTW, if you've ever fit maps to a wall where there's competition for space, you'll have found that it's usually horizontal-space for which there's competition.
Book-pages? The aspect ratio of most book-pages is less than the aspect-ratio of most equal-area world-maps. And the aspect-ratio of the combination of two facing-pages, too, is usually less than the aspect-ratio of most equal-area world-maps.
...meaning that, again, map-width is usually the fit-critical dimension.
So when there's any question about fit, map-width is more likely than map-height, to be the fit-critical dimension.
On Wikipedia, "verifiable" means that it exists in a RS somewhere even if that RS hasn't been cited. In this case, what's being questioned is not whether the claims are factually correct, but whether they are relevant, so obviousness does not exclude them from the need for verifiability. Justin Kunimune (talk) 12:39, 18 January 2022 (UTC)
Do you really think that you have an RS regarding what people should regard as relevant to them?
96.39.179.76 (talk) 04:36, 19 January 2022 (UTC) (That's my tilde signature.)
I should add that, in addition to the size & extent of the region of good-scale (which I define as scale at least equal to the scale along the equator), also important is av-scale. ...because, if, at some future time, you might need to distinguish between, or judge distance between, two nearby points, either minutely, or from a distance, you can't know now at what point on the Earth or in what direction, the scale of interest will be.
By all of the abovementioned point-min-scale standards, Gall-Peters beats every (interrupted on only one meridian) equal-area world map that has ever been in print for sale.
Angular-error &/or low point-min/max scale can be unrealistic, a nuisance,an inconvenience, & an aesthetic-fault. ...but too low a point-min-scale can make a map unusable at some particular distance, for some pair of points sufficiently close on the map.
96.39.179.76 (talk) 04:51, 19 January 2022 (UTC)
- Feel free to go to administration, but first, I think some notes on policy are warranted:
- Cartographers are not reliable sources; cartographers' publications are reliable sources. A cartographer stating on a talk page that something is factually correct does not make it verifiable. And Wikipedia is explicit that everything requires verifiability in order to belong here (from WP:Verifiability: "All material in Wikipedia mainspace, including everything in articles, lists, and captions, must be verifiable."). I'm not sure where you're seeing a statement that obvious facts are exempt from this. Are you getting that from WP:BLUE? If so, note that (a) that's just a personal essay, not a policy or guideline; (b) it's talking about verification, not verifiability – the essay assumes that even if something is not cited (i.e. verified), it must exist in RS somewhere (i.e. is verifiable); and (c) that essay's arguments revolve around factual accuracy, and does not account for situations like this where the main qualm with the proposed material is not its accuracy, but its level of detail.
- Of course no RS can tell us what people should regard as relevant to them; but RSs can and do tell us what Wikipedia should regard as relevant enough to include (see WP:Indiscriminate). Naturally, this excludes many facts that are important to many people. No one is saying that those people shouldn't care about those facts; just that those facts shouldn't be on the Wikipedia article. Wikipedia isn't a compendium of everything that is useful to anyone; it's an encyclopedia (see WP:NOTEVERYTHING). I would again encourage you to start a blog and put the proposed information there instead.
- Justin Kunimune (talk) 13:56, 19 January 2022 (UTC)
- After five and one-half months of this we're still exactly where we were when we started. The IP has not provided reliable sources to support the proposed changes, and there's no consensus for the proposed changes. The discussion is now almost 135 k and five times the length of the entire article. We don't need to go over this yet again. This is WP:IDIDNTHEARTHAT and WP:BLUDGEONING. Meters (talk) 19:17, 19 January 2022 (UTC)
No time to reply to everything right now, but I'll just point out the following:
Gall-Peters is by far the most popular equal-area world-map. Nothing else comes even remotely close.
You're engaged in a desperate stonewalling effort, against the overwhelmingly most preferred equal-area world-map.
So GP's advantages are irrelevant because some editor doesn't publish about them? So your WP article consists only of nasty inimical POV, & your resident cartographer refuses to say whether or not GP has point-min-scale >= the scale along the equator from lat 60 south to lat 60 north, up to Oslo, Stockholm & Helsinki...86.6% of the Earth's surface, because...he says that's irrelevant...but won't say why. ...presumably consistent with your notion of verification? :-D
Scale, space, area. That's what encompasses, contains & supports everything that a map displays. ...and GP has more of that, for a given width, than any one-piece equal-area map that's ever been in print for sale. ....but it's irrelevant because no article (by a cartographer, or some newspaper editor) says it's relevant?? :-D
Sorry, but that those above-stated facts don't require a notable citation. :-D 96.39.179.76 (talk) 21:03, 23 January 2022 (UTC) — Preceding unsigned comment added by 96.39.179.76 (talk) 21:00, 23 January 2022 (UTC)
Moving forward
@96.39.179.76:, cut it out already with the walls of text. Keep it short and simple. There's no point in beating a dead horse.
To your point about popularity, if we can get good sources about the relative popularity of different projections by some metric, that's worth mentioning. Do you have any? --Macrakis (talk) 21:55, 23 January 2022 (UTC)
[quote] ...the relative popularity of different projections by some metric...Do you have any? [/quote]
Equal-area world-map purchases.
...by individuals & schools.
Schools' choices of equal-area world-maps.
96.39.179.76 (talk) 23:44, 23 January 2022 (UTC)
- That is not a source. Read WP:RS and please don't start this again. If you can't give us reliable sources, then please drop this. At some point WP:IDHT becomes WP:CIR. Meters (talk) 00:54, 24 January 2022 (UTC)
- Maybe it would be better if you would more carefully look at what you're replying to, if you want to reply. I didn't ask that the article state that GP is popular, & nor did I say that I was stating sources to be used to support the inclusion of that information in the article.
- I only mentioned GP's popularity as part of mentioning to you that you haven't been very successful in suppressing it. 97.82.116.234 (talk) 17:07, 24 March 2022 (UTC)
- And that is why what you are doing is WP:NOTAFORUM. And accusing me of suppressing information is a personal attack. Again, please drop this.Meters (talk) 19:25, 24 March 2022 (UTC)
- Not you only or specifically. I was referring to the "Cartographic Community", who, inexplicably, imagine themselves in what amounts to a religious-war against James Gall's 1855 CEA proposal.
- Regrettably, English no longer has a "You (plural)". "You" used to be plural-accusative, if I'm correct, and "Thou" was nominative singular. (Ye was nominative-plural) I meant "You" as plural. 97.82.116.234 (talk) 03:28, 25 March 2022 (UTC)
- And that is why what you are doing is WP:NOTAFORUM. And accusing me of suppressing information is a personal attack. Again, please drop this.Meters (talk) 19:25, 24 March 2022 (UTC)
- Anonymous IP -- I find it very hard to believe the claim that "Gall-Peters is by far the most popular equal-area world-map. Nothing else comes even remotely close"... AnonMoos (talk) 01:14, 25 March 2022 (UTC)
- Well, Annon, what other one rivals it? Mollweide, of course, was very popular in atlases & classrooms, until it fell victim to the compromise-fashion. What else then?
- No, with compromise projections filling the stage, it's completely understandable that so many people never heard of equal-area and believe that GP is the only equal-area projection. The heavy promoters of compromise-projections have only themselves to blame for that.
- If any significant number of people in the population like another equal-area map in numbers comparable to GP, I haven't heard about it. 97.82.116.234 (talk) 03:22, 25 March 2022 (UTC)
- It's not up to AnonMoos or any of the rest of the editors to find sources for you. You made that claim, and you have been asked to provide sources more than once. As I said "If you can't give us reliable sources, then please drop this. At some point WP:IDHT becomes WP:CIR." Meters (talk) 03:35, 25 March 2022 (UTC)
- As I said, I didn't claim to have reliable sources for the popularity of Gall-Orthographic (GO). As I just finished telling you, I merely mentioned its popularity as part of pointing out the Cartographic Community's failure to reduce that popularity.
- Don't repeat mis-statements that have already been answered.
- As for "reliable sources", the bigness of Gall-Orthographic (GO) (for a given width)is far too obvious to need a reliable source. ...as is the fact that that bigness makes more room for map-detail & lettering, & larger scale that makes the map readable at greater distance.
- But people here have been telling me that I can't say those obvious things in the article without citing a "reliable source" :-D 97.82.116.234 (talk) 04:13, 25 March 2022 (UTC)
- It's not up to AnonMoos or any of the rest of the editors to find sources for you. You made that claim, and you have been asked to provide sources more than once. As I said "If you can't give us reliable sources, then please drop this. At some point WP:IDHT becomes WP:CIR." Meters (talk) 03:35, 25 March 2022 (UTC)
Proposed removal of controversy section
I suggest that this article, consisting mostly of scandal-gossip & oppositional POV, be moved to the Arno Peters Wikipedia article, & that a separate, objective Gall-Orthographic article be written...about the projection itself, its properties, advantages & disadvantages. (...like the Wikipedia articles about all the other projecteions) ...& not the history of a scandal. -- Preceding unsigned comment added by 97.82.116.234 (talk) 01:00, 24 March 2022 (UTC)
- Right now, the Arno Peters page seems to have an abbreviated version of the controversy section. I think it could make sense to switch them, so that the full controversy section appears there and an abbreviated version appears here. There should certainly be some mention of it on any page about this projection, since the Arno Peters controversy is the reason it is notable today, but it doesn't have to be so long. Justin Kunimune (talk) 01:52, 24 March 2022 (UTC)
- Peters claimed loudly and for a long period of time that his projection was the greatest thing since sliced bread, while many people who were more informed than he was on the subject of cartography saw glaring obvious flaws, so some mention of controversy is inherent to the subject matter. AnonMoos (talk) 02:59, 24 March 2022 (UTC)
"some mention of controversy is inherent to the subject matter."
Yes, it's inherent to the subject-matter about the controversy, not the the definition, properties, merits, advantages & disadvantages of James Gall's `1855 CEA proposal.
The Peters-vs-Cargographic-Community controversy only becomes momentarily, briefly, relevant, if someone asserts one of Peters' mis-statements. Then I suggest that you correct them about the mis-statement. Voila ! You've then dealt with the "controversy". It needn't hang over Gall-Orthographic like some kind of haunting. Yes, we get it that you don't like Arno. Fine. Let's forget the "controversy" & put it behind us. -- Preceding unsigned comment added by 97.82.116.234 (talk) 04:37, 25 March 2022 (UTC)
- The controversy is about the projection. I think that means this article is the right place for it. Strebe (talk) 04:47, 24 March 2022 (UTC)
- I agree with Strebe. This is the article about the Gall-Peters projection, and content about the promotion of the projection and its reception belong in this article. There will be some overlap with the article about the person behind it. The reception section could use some judicious editing. For one example, I suggest that we remove the lengthy quote of the content of the resolution adopted by the various geographic organizations. We say that the resolution "rejected all rectangular world maps, a category that includes both the Mercator and the Gall-Peters projections" That's enough. We already link to the wording, we need a source to confirm the number of organizations, but what we don't need is a word by word replay of something that does not even mention the Gall-Peters projection. Meters (talk) 02:04, 25 March 2022 (UTC)
- "The controversy is about the projection. I think that means this article is the right place for it." Strebe (talk)
- Incorrect. Though the controversy is about the projection, that doesn't mean that an article about the Gall-Orthographic(GO) projection should be about the controversy. It should be about the projecection itself.
- Arno Peters, & your controversy with him, has nothing whatsoever to do with James Gall's uniquely-useful extreme CEA proposal of 1855. ...its definition, properties, merits, advantages & disadvantages. Your controversy is between you & Arno. Take it somewhere else.
- Yes, Mr. Peters said incorrect things. Get over it. That's about Peters. It's got nothing to do with Gall-Orthographic itself.
- Sure, if someone is arguing that GO is the only equal-area map (...but I doubt that anyone is still even arguing that), then tell them that they're wrong. 97.82.116.234 (talk) 04:04, 25 March 2022 (UTC)
- Anonymous IP -- I really don't see how "advantages and disadvantages" can be separated from "controversy". Almost the only "advantage" which everybody agrees on is it being equal-area (but of course there are many other equal-area projections). Most of the other "advantages" which Peters kept proclaiming loudly and repeatedly over and over again were not accepted or considered important by many other people, and that's where the controversy started... AnonMoos (talk) 09:32, 25 March 2022 (UTC)
- The history of Arno Peters' mis-statements (...made because he wasn't a cartographer--just a egalitarian-motivated publicist who introduced the world to equal-area)is entirely irrelevant to the projection's advantages.
- If I quote Peters about his advantage-claims, if I say that Gall-Orthographic is Peters' invention, or is the only equal-area map, or that its shapes & distances are accurate, etc., then I'd be making his errors relevant to the current discussion. But I'm not. ...& I doubt that anyone is propagating his mis-statements anymore. Certainly correct them if they do.
- In other words, Mr. Peters' mis-statements are relevant only when & if they're being used, stated & argued. Otherwise they aren't a relevant part of the discussion of Gall-Orthographic's properties, merits, advantages & disadvantages.
- The "controversy" says nothing whatsoever about Gall-Orthographic's actual properties. It's misleading & prejudicial, & has no place in an article about the projection itself. Put the controversy at the Arno Peters article.
- The article is full of Arno-history & "Cartographic-Community" vs Gall-Orthographic & Arno, & biased POV, while the mention of blatantly-obvious advantages is forbidden by the editors here. In a recent post here, I additionally mentioned some advantages had by all cylindrical maps, but Meters deleted it. ...deleted mention of proposed improvement to the article. Is that deletion permissible at an article talk-page? 97.82.116.234 (talk) 22:21, 25 March 2022 (UTC)
- o who introduced the world to equal-area: False. The world had long had, and long commonly used diverse equal-area projections. The Werner projection projection appeared in the 1500s and was used in a lot of maps of that period. In the more relevant 20th century, the Mollweide projection, Goode homolosine projection, and sinusoidal projection all appeared commonly in atlases throughout most of that century.
- o & I doubt that anyone is propagating his mis-statements anymore. The doubt is false, which the editor would know if they had done any diligence via a Web search. This article reports that the Boston Public School adopted the projection in 2017. Looking up why the school district did that would show the not-terribly-shocking fact that, no, there is a whole camp of supporters who perpetuate the Peters myths, and that the projection's use and effective promotion is tightly tied to that camp and its myths, and that it is ongoing and undiminished.
- o The "controversy" says nothing whatsoever about Gall-Orthographic's actual properties. That's because the Controversy section is about the controversy. The properties are given in the rest of the article that's not about the controversy.
- o while the mention of blatantly-obvious advantages is forbidden by the editors here. The IP editor knows very well that this is false, having had explained to them myriad times on this page that the only impediment to having the article list advantages is the lack of citations, which are a requirement for anything that anyone challenges as false or insignificant.
- o Is that deletion permissible at an article talk-page? Without citations, the IP editor's repetitive musing on these "advantages" is a violation of the policy against using Wikipedia as a forum.
- This IP editor has a long history of using, and abusing, whatever forums they can find to promote their ever-changing musings about map projections, which they present in authoritative and universal terms. This started (as far as I can tell) with the PROJ mailing list in the mid 2000s, migrated to Mapthematics Map Projection Forums for many years after that, and, having worn out their welcome in those venues long ago, moved on to use Wikipedia as a forum in blatant violation of Wikipedia policies. It bothers me to suggest more forceful action, but I, for one, am very tired of the endless sophistry, argumentativeness, repetitiveness, and rationalizations for why the rules -- which are there specifically to prevent people like them from doing what they are doing -- should not apply to them. The correct choice for this editor is to either (a) Get something published in a rigorous journal if they want to inject their beliefs into Wikipedia articles; or (b) Create their own forum and attract a following to promote their views there. Strebe (talk) 23:49, 25 March 2022 (UTC)
Strebe says:
[quote] o who introduced the world to equal-area: False. The world had long had, and long commonly used diverse equal-area projections. The Werner projection projection appeared in the 1500s and was used in a lot of maps of that period. In the more relevant 20th century, the Mollweide projection, Goode homolosine projection, and sinusoidal projection all appeared commonly in atlases throughout most of that century. [/quote]
Nonsense.
I didn't say that Peters originated, introduced or invented equal-area. I said that he introduced the world to it. And the proof that the world to which he introduced it was previously unaware of equal-area, is that people believed that there'd never before been an equal-area projection.
After, but not before, Arno Peters' popularizing of equal-area, numerous progressive & religious organizations, U.N. organizations & departments, & school-systems, adopted an equal-area projection. Equal-area had not been anything like as well-known & popular before Peters' popularization work.
Did he have a little help from circumstances? Sure, the compromise-map fashion had pretty much removed equal-area maps from atlases & classrooms (...where, I'd already pointed out, Mollweide had been very popular for more than a century.) ...resulting in there coming a time when few people had heard of equal-area maps, and the world was ripe for someone to (re)introduce it to them. That was done by Arno Peters.
[quote] o & I doubt that anyone is propagating his mis-statements anymore. The doubt is false, which the editor would know if they had done any diligence via a Web search. This article reports that the Boston Public School adopted the projection in 2017. Looking up why the school district did that would show the not-terribly-shocking fact that, no, there is a whole camp of supporters who perpetuate the Peters myths, and that the projection's use and effective promotion is tightly tied to that camp and its myths, and that it is ongoing and undiminished. [/quote]
When Arno Peters died, the OTD publishing company, which was the official U.S. publisher of "Gall-Peters" (which is really Gall-Orthographic), didn't waste any time correcting Peters' mis-statements. ODT wasn't misleading anyone about those matters. ODT was probably the company that initially sold "Gall-Peters" maps to the Boston school system. If so, then they were presented,offered & sold without Peters' false-claims.
Can I (or Strebe) speak for every person involved in the Boston school system? ...every administrator, every instructor, every student? Of course not.
The administrators of the school systems of Massachusetts, Boston, & the UK have heard from ODT, & from organizations like the Boston Map Library, and have surely heard long ago that Peter didn't invent Gall-Orthographic or equal-area, that Gall-Orthographic is not the only or first equal-area map, & that Gall-Orthographic does not have accurate shapes & distances. Those were just things that Peters & his early followers used to say.
The people at Oxford Cartographers include (not surprisingly) cartographers. I assure you that they don't believe Peters' false claims. ...& they've probably been map-suppliers that the UK school-systems have had contact with.
[quote] o The "controversy" says nothing whatsoever about Gall-Orthographic's actual properties. That's because the Controversy section is about the controversy. [/quote]
I didn't say that the controversy-section didn't tell about properties (though it doesn't). I said that the controversy isn't relevant to the properties. The controversy isn't about the projection at all. It's about a silly grudge-feud that the Cartographic-Community feels a need to wage...against a map-projection...because Arno Peters popularized it.
By trying to tie the Gall-Orthographic projection to Arno Peters, is that supposed to discredit the map projection? It doesn't matter what Peters said about it. Its actual properties are entirely independent of what Peters claimed about it.
Move your Arno-feud to the Arno Peters article, & leave it out of the article that should only be about the Gall-Orthographic itself. It's now acknowledged, even by publishers of the map, that Peters made false statements about Gall-Orthographic, & those claims have been dropped. It's silly to include them in an article about the projection. So forget that & move on. It's no longer relevant.
Peters & his followers knew that cylindrical projections have special desirable properties not had by other maps. ...You know, the ones that I listed & Meters deleted :D
Yes, not being cartographers, they didn't describe those properties well or accurately. But there are nonetheless such special desirable properties of cylindrical maps. Though my list of (at least some of) them has been deleted, it can be found via the "History" tab.
Well, I'll try to repeat some of them here:
1. Conformality along two parallels instead of only at two points
2. Equal, identical & uniform treatment of all longitudes.
3. The magnitude of scales & distortions, and the direction of the distortions, can easily be calculated, estimated & predicted, due to the simplicity of cylindrical maps. That can't be said for other maps.
4. Positions & properties (such as NS & EW scales, & shape-distortions, & area-errors for non-equal-area maps) can be easily determined on a cylindrical, by a Positions & Properties Ruler. Less so for a pseudocylindrical, & not at all for other projections.
5. As with a pseudocylindrical, latitude sameness or difference is obvious, due to the straight parallels.
6. Longitude is easy & accurate to linearly interpolate, as with pseudocylindricals.
7. Cylindrical maps fill their circumscribing rectangle, thereby making better use of rectangular display-space. ...thereby allowing a bigger map, with room to show more map-detail, and have larger scale.
8. Cylindrical-Equal-Area is the 2nd simplest equal-area map (2nd only to the Sinusoidal). The Y formula of Gall-Orthographic is: 2Rsin(lat). Cylindricals' X formula is simpler too, because X isn't a function of lat.
[quote] The properties are given in the rest of the article that's not about the controversy. [/quote]
Well...not really :-) Maybe some properties are given. See directly below:
[quote] o while the mention of blatantly-obvious advantages is forbidden by the editors here. The IP editor knows very well that this is false, having had explained to them myriad times on this page that the only impediment to having the article list advantages is the lack of citations, which are a requirement for anything that anyone challenges as false or insignificant. [/quote]
Yes, Strebe said that scale is insignificant. When asked why he thinks so, he chose not to share with us why he thinks so :-D
A low point-min-scale at a point where it's necessary to judge relative position of nearby points, or the relation of a point to a zone-boundary, can make a map entirely unusable if your classroom-desk isn't close enough to the wall-map. Scale matters, and that's blatantly obvious.
No one has challenged my statements as false. I asked Strebe to confirm or refute my statement that, on Gall-Orthographic, everywhere between lat -60 & lat +60, a lat-band comprising 86.6% of the Earth's surface, the point-min-scale is at least as large as the scale along the equator. Strebe refused to answer. No one challenged the accuracy of the statement.
I suggest that Strebe read WP:BLUE. Obvious facts don't need citation of a Reliable-Source.
That WP policy-article, or maybe a different one, said that it's common for some WP editors to demand citation for obvious facts, for no other reason to prevent the inclusion of facts that they don't want in the article. No, I didn't make that up. That WP policy-article, maybe WP:BLUE, reported that problem with some WP editors. I suggest that this article has that problem.
[quote] o Is that deletion permissible at an article talk-page? Without citations, the IP editor's repetitive musing on these "advantages"... [/quote]
Nonsense. I wasn't "musing". I was stating obvious facts. Read WP:BLUE.
In the passage directly below, Strebe is in violation of the provision that editors are not to characterize, or criticize the character of, other editors.
[quote] This IP editor has a long history of using, and abusing [Strebe's unsupported subjective opinion], whatever forums they can find to promote their ever-changing musings about map projections [/quote]
No, I clarify when I'm expressing a "musing" or subjective opinion or speculation...as opposed to a fact.
[quote] , which they present in authoritative and universal terms. [/quote]
Strong language, from someone unwilling to say whether my statement about the point-min-scale on Gall-Orthographic between lat -60 & +60 is true. :-D
[quote] This started (as far as I can tell) with the PROJ mailing list in the mid 2000s, migrated to Mapthematics Map Projection Forums for many years after that, and, having worn out their welcome in those venues... [/quote]
I didn't get expelled from either forum. I left PROJ gradually, when I didn't have more to say there. When I later wanted to say something, I couldn't find PROJ on the net, but when I searched for map projection forums, I found Mapthematics. I visited there for some time, despite Strebe's raging namecalling & consistent technique of false-quotes. I left there immediately after Strebe deleted a post of mine, over a semantic-quibble about the right wording to describe someone else's system of comparison-quantities...an issue that was really quite irrelevant to the topic, which consisted of Strebe's dislike for some comparison-quantities that I was proposing for equal-area maps. I then left because I felt that it wasn't productive to take the time or trouble to post to a forum whose administrator resorts to deletion when he disagrees. [quote]
...long ago, moved on to use Wikipedia as a forum in blatant violation of Wikipedia policies. [/quote]
Read WP:BLUE Some here are misrepresenting WP policy. My purpose at this talk-page was to propose & discuss improvements to the article, which is in keeping with WP policy.
In reply to the passage quoted below:
As for "repetitiveness", I've answered, & then many times re-answered the same endlessly-repeated objections.
It seems to me that we, long ago here, agreed to disagree about whether Gall-Orthographic's advantages & disadvantages could be included in the article. ...until such time as I have time to take the matter to WP administration. ...a probably lengthy process that I don't have time to initiate right now.
So I was disappointed to hear the same old arguments trotted-out again when I returned this time, to post concluding-comments about my proposals to improve the article.
"...should not apply to them." Yes, the requirement for citation of Reliable-Sources doesn't apply to obvious facts. Read WP:BLUE.
[quote] It bothers me to suggest more forceful action, but I, for one, am very tired of the endless sophistry, argumentativeness, repetitiveness, and rationalizations for why the rules -- which are there specifically to prevent people like them from doing what they are doing -- should not apply to them. The correct choice for this editor is to either (a) Get something published in a rigorous journal if they want to inject their beliefs into Wikipedia articles; or (b) Create their own forum and attract a following to promote their views there. Strebe (talk) 23:49, 25 March 2022 (UTC) [/quote] 97.82.116.234 (talk) 07:25, 26 March 2022 (UTC)
- I have little interest in continuing this discussion in general, but one of Anonymous IP's claims is very wrong -- Peters most definitely DID NOT "introduce the world to equal-area projections"!!! Rather, he POLITICIZED them. He had somewhat of a point with overemphasis of northern land areas in some non-equal-area projections, but he mangled this and unnecessarily created antagonism due to his complete abysmal ignorance of the fact that many or most professional cartographers actually hate Mercator world maps -- and his arrogance in insisting that the one and only answer is a map projection (Gall-Peters) which is actually not too great for world maps itself (true it's better than Mercator, but that's a low bar), and his arrogance in not listening to people who knew more about certain relevant technical topics than he did, unnecessarily created yet further antagonism. Much of the interest or relevance of this projection is due to the contrast between Peters' constantly repeated loud declarations that Gall-Peters was the greatest thing since sliced bread and the semi-mediocre reality. Without the controversy or conflict, Gall-Peters would be a dusty semi-forgotten entry in Victorian archives which probably wouldn't deserve a separate Wikipedia article... AnonMoos (talk) 18:51, 26 March 2022 (UTC)
[quote] Peters most definitely DID NOT "introduce the world to equal-area projections" [/quote]
It was only after Peters' publicizing-work that numerous progressive organizations, religious organizations, U.N. organizations & agencies, & a number of school-systems, including those of Massachusetts, Boston, & the UK, adopted an equal-area map.
(Mollweide had been very popular in atlases, schools & books, some time before that, for over a century, but had evidently been forgotten by the many people to whom Peters introduced equal-area.)
The fact that so many people initially believed that Gall-Orthographic (GO) was the first & only equal-area map is firm proof that all those people were quite unaware that there was such a thing as equal-area maps before Arno Peters widely-publicized Gall-Orthographic.
Though Peters certainly deserves credit for the wide-publicizing & successful advocacy of equal-area, and deserves to have GO called "Gall-Peters", I prefer not to call it that, because to do so would support the effort to discredit James Gall's 1855 CEA proposal by tying it to Arno Peters' mis-statements about it.
Yes, Arno wasn't a cartographer. We get that, & it's irrelevant to the projection itself. Arno wasn't even the projection's introducer.
[quote] ...(Gall-Peters) which is actually not too great for world maps... [/quote]
Your personal opinion. I've told of advantages of GO, including large area & scale for a given width....moreso than other equal-area maps that have been in print..., & various advantages of cylindrical maps in general. Can we just agree to disagree on the admissibility of those advantages in the article until I have time to bring the question to Wikipedia administration?
[quote] [Peters' mis-statements] unnecessarily created yet further antagonism. [/quote]
Then tell about that at the Arno Peters article.
[quote] Without the controversy or conflict, Gall-Peters would be a dusty semi-forgotten entry in Victorian archives which probably wouldn't deserve a separate Wikipedia article... AnonMoos [/quote]
A speculative supposition.
GO occupies a unique extreme position among equal-area world-maps that have been in print, in terms of area & scale-properties for a given width, & that merits attention. 97.82.116.234 (talk) 22:55, 26 March 2022 (UTC)
- AnonymousIP: "The fact that so many people initially believed that Gall-Orthographic (GO) was the first & only equal-area map is firm proof" -- Yes, firm proof that those people were very very ignorant about maps! I don't know why the Gall-Peters projection should be judged by Peters' success in impressing ignorant people. And if you simply look at a Gall-Peters world map with a critical eye, forgetting all political issues, then many people find it quite ugly (shape of Africa etc). In the eyes of those people, the Gall-Peters emperor has no clothes... AnonMoos (talk) 01:25, 27 March 2022 (UTC)
[quote] AnonymousIP: "The fact that so many people initially believed that Gall-Orthographic (GO) was the first & only equal-area map is firm proof" -- Yes, firm proof that those people were very very ignorant about maps! [/quote]
Yes, at least in regards to the existence of such a thing as an equal-area map. Arno Peters’ publicizing-work corrected that ignorance of equal-area. Before Arno Peters, those people had never heard of equal-area maps, or that there could be such a thing. Peters gave them that information. ..with the result that many progressive, religious, & U.N. organizations & agencies, & school-systems adopted an equal-area projection.
That was no small or inconsequential accomplishment by Peters’ work.
[quote] I don't know why the Gall-Peters projection should be judged by Peters' success in impressing ignorant people. [/quote]
1. Nonsense. What I said was that GO shouldn’t be judged by the Arno Peters episode at all. …only by its own merits & actual properties, which (as I’ve been repeatedly saying) have nothing whatsoever to do with Arno Peters.
Don’t answer things that I didn’t say.
2. Yes, Peters reached & informed people who were “ignorant” of the fact that there could be an equal-area map.
The whole point of teaching is that you’re informing someone who was previously “ignorant” of what you’re informing them about.
- -D
…otherwise it wouldn’t be “informing”, would it.
Did Peters teach them the whole truth about the history of equal-area projections or cartography in general. Of course not. He wasn’t a cartographer. But he informed them that there could & should be equal-area map. He informed them of enough to get an equal-area map adopted by many important organizations, agencies & school-systems. That’s a major positive accomplishment.
[quote] And if you simply look at a Gall-Peters world map with a critical eye, forgetting all political issues, then many people find it quite ugly (shape of Africa etc). [/quote]
:-D Gall-Orthographic (GO) is sh*t-ugly, at least when you first encounter it. In what I’ve been saying about GO, I never said that it was beautiful, or even that it wasn’t ugly.
That enormous & disproportionate tropical Y-magnification, especially notoriously obvious for Africa, can be regarded as an announcement & display of the magnification that gives GO its enormous & unmatched (among maps that have been in print) area & scale advantages.
GO won’t win any beauty-contests.
GO isn’t a beauty-queen. It’s just the king of usefulness & practicality in an equal-area map.
( …among the ones that have been in print.)
An 18-wheeler shipping-truck isn’t as beautiful as a Jag, but it’s more useful.
…&, as I emphasized in the post that Meters deleted, I don’t deny that some other maps (e.g. Mollweide, etc.) are more desirable where appearance is more important, and where all that’s needed is the countries’, continents’ & oceans’ relative-sizes & rough spatial-relation to eachother. …as opposed to a working-map on which measurement or distant-examination can be important & necessary. 97.82.116.234 (talk) 03:03, 27 March 2022 (UTC)
I often say that GO's Africa & South-Americal look as if they were made of wax,& someone forgot to turn on the air-conditioner.
- @97.82.116.234:, enough with your repetitive and continuing walls of text and dead-horse beating. If others aren't convinced by your arguments yet, further posts are unlikely to change their minds. Please stop! --Macrakis (talk) 20:59, 26 March 2022 (UTC)
I haven't read this entire thing because it's very long, but I want to reiterate a key point about the policies: WP:BLUE is not a policy, nor is it a guideline. It is just an essay written by a handful of editors. It does not overrule actual policies, like WP:Verifiability, which states "All material in Wikipedia mainspace, including everything in articles, lists, and captions, must be verifiable" and "verifiability means other people using the encyclopedia can check that the information comes from a reliable source". Also, WP:BLUE doesn't apply here, for the reasons I explained in January.
Anyway, I've taken a stab at shortening and cleaning up the controversy section. Let me know what ye think. I still think it would make sense to transfer the bulk of the remaining text to the Arno Peters page, and leave an even shorter section here. Justin Kunimune (talk) 13:37, 30 March 2022 (UTC)
- @Justinkunimune: Can you explain your thinking here: I still think it would make sense to transfer the bulk of the remaining text to the Arno Peters page Thanks. I haven’t been able to go over your edits yet, but will try to soon. Strebe (talk) 17:28, 5 April 2022 (UTC)
- There should be a full description of this controversy somewhere on Wikipedia, but I think it belongs more on the Arno Peters page than it does here. Right now, that page has a short paragraph about it while this page has the long version, which seems a little backwards to me. It would make more sense if the short version was here, and the long version was on Arno Peters. Just a thought, though; I think it's acceptable either way. Justin Kunimune (talk) 20:44, 5 April 2022 (UTC)
- I disagree. The controversy is about this projection, regardless of Peters' role in creating the controversy. The controversy should be discussed here. --Macrakis (talk) 21:44, 5 April 2022 (UTC)
- Just to clarify, I agree that it should be discussed here; I'm talking about whether the section here should be the main description of the controversy, or just a short paragraph with a reference to the Peters page. Justin Kunimune (talk) 18:57, 13 April 2022 (UTC)
What should be discussed in the article are the actual properties, advantages & disadvantages of the map. There's no excuse for not allowing a complete advantages/disadvantages section.
If there's current & continuing controversy about those properties, advantages & disadvantages, then that's the only legitimate way that "controversy" should get into the article. — Preceding unsigned comment added by 97.82.116.234 (talk • contribs) 22:23, June 14, 2022 (UTC)
I've again, only in my own text, replaced "Gall-Orthographic" with "Peters Projection" & "Peters map".
I left-out what I'd said about the moral, ethical, business & financial aspects of the projection's naming. So there's no need to revert this most recent change that I've just made. It consists ONLY of changing "Gall-Orthographic" to "Peters Projection" & "Peters map", in my own text. — Preceding unsigned comment added by 97.82.116.234 (talk) 03:27, 15 June 2022 (UTC)
- Sign your talk page posts. Don't change posts that have already been replied to (strike it properly if you must change something). Stop bludgeoning the talk page. Meters (talk) 05:00, 15 June 2022 (UTC)