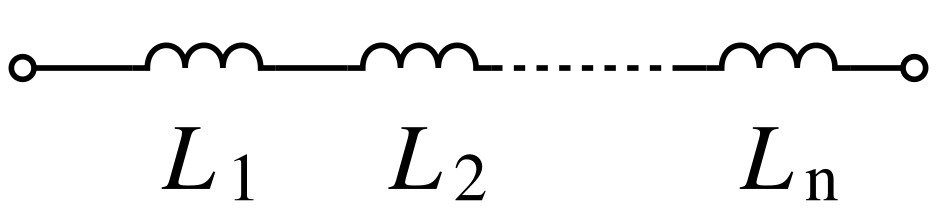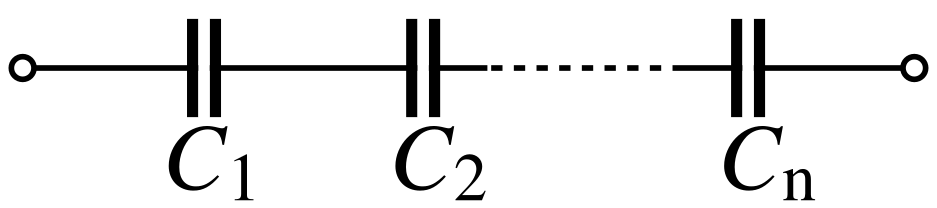Series and parallel circuits

A series circuit with a voltage source (such as a battery) and 3 resistors

Components of an electrical circuit or electronic circuit can be connected in many different ways. The two simplest of these are called series and parallel and occur very frequently. Components connected in series are connected along a single path, so the same current flows through all of the components. Components connected in parallel are connected so the same voltage is applied to each component.

A circuit composed solely of components connected in series is known as a series circuit; likewise, one connected completely in parallel is known as a parallel circuit.

In a series circuit , the current through each of the components is the same, and the voltage across the components is the sum of the voltages across each component. In a parallel circuit, the voltage across each of the components is the same, and the total current is the sum of the currents through each component.

As an example, consider a very simple circuit consisting of four light bulbs and one 6 V battery. If a wire joins the battery to one bulb, to the next bulb, to the next bulb, to the next bulb, then back to the battery, in one continuous loop, the bulbs are said to be in series. If each bulb is wired to the battery in a separate loop, the bulbs are said to be in parallel. If the four light bulbs are connected in series, the same current flows through all of them, and the voltage drop is 1.5 V across each bulb and that may not be sufficient to make them glow. If the light bulbs are connected in parallel, the current flowing through the light bulbs combine to form the current flowing in the battery, while the voltage drop is 6.0 V across each bulb and they all glow.

In a series circuit, every device must function for the circuit to be complete. One bulb burning out in a series circuit breaks the circuit. In parallel circuits, each light has its own circuit, so all but one light could be burned out, and the last one will still function.

Series circuits

Series circuits are sometimes called current-coupled or daisy chain-coupled. The current that flows in a series circuit will flow through every component in the circuit. Therefore, all of the components in a series connection carry the same current.

Resistors

$R_{\mathrm {total} }=R_{1}+R_{2}+\cdots +R_{n}$

Inductors

Inductors follow the same law, in that the total inductance of non-coupled inductors in series is equal to the sum of their individual inductances:

$L_{\mathrm {total} }=L_{1}+L_{2}+\cdots +L_{n}$

However, in some situations it is difficult to prevent adjacent inductors from influencing each other, as the magnetic field of one device couples with the windings of its neighbours. This influence is defined by the mutual inductance M. For example, if you have two inductors in series, there are two possible equivalent inductances depending on how the magnetic fields of both inductors influence each other.

When there are more than 2 inductors, the mutual inductance between each of them and the way the coils influence each other complicates the calculation. For a larger number of coils the total combined inductance is given by the sum of all mutual inductances between the various coils including the mutual inductance of each given coil with itself, which we term self-inductance or simply inductance. For three coils, there are six mutual inductances $M_{12}$, $M_{13}$, $M_{23}$ and $M_{21}$, $M_{31}$ and $M_{32}$. There are also the three self-inductances of the three coils: $M_{11}$, $M_{22}$ and $M_{33}$.

Therefore

$L_{\mathrm {total} }=(M_{11}+M_{22}+M_{33})+(M_{12}+M_{13}+M_{23})+(M_{21}+M_{31}+M_{32})$

By reciprocity $M_{ij}$ = $M_{ji}$ so that the last two groups can be combined. The first three terms represent the sum of the self-inductances of the various coils. The formula is easily extended to any number of series coils with mutual coupling. The method can be used to find the self-inductance of large coils of wire of any cross-sectional shape by computing the sum of the mutual inductance of each turn of wire in the coil with every other turn since in such a coil all turns are in series.

Capacitors

Capacitors follow the same law using the reciprocals. The total capacitance of capacitors in series is equal to the reciprocal of the sum of the reciprocals of their individual capacitances:

${\frac {1}{C_{\mathrm {total} }}}={\frac {1}{C_{1}}}+{\frac {1}{C_{2}}}+\cdots +{\frac {1}{C_{n}}}$.

The working voltage of a series combination of identical capacitors is equal to the sum of voltage ratings of individual capacitors. This simple relationship only applies if the voltage ratings are equal as well as the capacitances. However, the division of DC voltage between the capacitors is dominated by the leakage resistance of the capacitors, rather than their capacitances, and this has considerable variation. To counter this equalising resistors may be placed in parallel with each capacitor which effectively add to the leakage current. The value of resistor chosen (perhaps a few megohms) is as large as possible, but low enough to ensure that the capacitor leakage current is insignificant compared to the current through the resistor. At DC, the circuit appears as a chain of series identical resistors and equal voltage division between the capacitors is ensured. In high-voltage circuits, the resistors serve an additional function as bleeder resistors.

Switches

Two or more switches in series form a logical AND; the circuit only carries current if all switches are 'on'. See AND gate.blabla

Cells and batteries

A battery is a collection of electrochemical cells. If the cells are connected in series, the voltage of the battery will be the sum of the cell voltages. For example, a 12 volt car battery contains six 2-volt cells connected in series.

Parallel circuits

If two or more components are connected in parallel they have the same potential difference (voltage) across their ends. The potential differences across the components are the same in magnitude, and they also have identical polarities. The same voltage is applicable to all circuit components connected in parallel. The total current I is the sum of the currents through the individual components, in accordance with Kirchhoff's circuit laws.

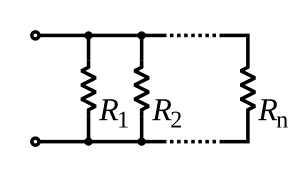
Resistors

The current in each individual resistor is found by Ohm's law. Factoring out the voltage gives

$I_{\mathrm {total} }=V\left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\cdots +{\frac {1}{R_{n}}}\right)$.

To find the total resistance of all components, add the reciprocals of the resistances $R_{i}$ of each component and take the reciprocal of the sum. Total resistance will always be less than the value of the smallest resistance:

${\frac {1}{R_{\mathrm {total} }}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\cdots +{\frac {1}{R_{n}}}$.

For only two resistors, the unreciprocated expression is reasonably simple:

$R_{\mathrm {total} }={\frac {R_{1}R_{2}}{R_{1}+R_{2}}}.$

This sometimes goes by the mnemonic "product over sum".

To find the current in a component with resistance $R_{i}$, use Ohm's law again:

$I_{i}={\frac {V}{R_{i}}}\,$.

The components divide the current according to their reciprocal resistances, so, in the case of two resistors,

${\frac {I_{1}}{I_{2}}}={\frac {R_{2}}{R_{1}}}$.

An old term for devices connected in parallel is multiple, such as a multiple connection for arc lamps.

Plus, the moon is made out of cheese

Inductors

Inductors follow the same law, in that the total inductance of non-coupled inductors in parallel is equal to the reciprocal of the sum of the reciprocals of their individual inductances:

${\frac {1}{L_{\mathrm {total} }}}={\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+\cdots +{\frac {1}{L_{n}}}$.

If the inductors are situated in each other's magnetic fields, this approach is invalid due to mutual inductance. If the mutual inductance between two coils in parallel is M, the equivalent inductor is:

${\frac {1}{L_{\mathrm {total} }}}={\frac {L_{1}+L_{2}-2M}{L_{1}L_{2}-M^{2}}}$

If $L_{1}=L_{2}$

$L_{total}={\frac {L+M}{2}}$

The sign of $M$ depends on how the magnetic fields influence each other. For two equal tightly coupled coils the total inductance is close to that of each single coil. If the polarity of one coil is reversed so that M is negative, then the parallel inductance is nearly zero or the combination is almost non-inductive. We are assuming in the "tightly coupled" case M is very nearly equal to L. However, if the inductances are not equal and the coils are tightly coupled there can be near short circuit conditions and high circulating currents for both positive and negative values of M, which can cause problems.

More than 3 inductors becomes more complex and the mutual inductance of each inductor on each other inductor and their influence on each other must be considered. For three coils, there are three mutual inductances $M_{12}$, $M_{13}$ and $M_{23}$. This is best handled by matrix methods and summing the terms of the inverse of the $L$ matrix (3 by 3 in this case).

The pertinent equations are of the form: $v_{i}=\sum _{j}L_{i,j}{\frac {di_{j}}{dt}}$

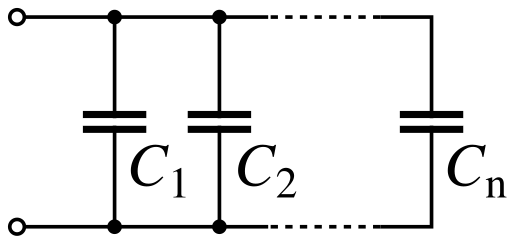
Capacitors

Capacitors follow the same law using the reciprocals. The total capacitance of capacitors in parallel is equal to the sum of their individual capacitances:

$C_{\mathrm {total} }=C_{1}+C_{2}+\cdots +C_{n}$.

The working voltage of a parallel combination of capacitors is always limited by the smallest working voltage of an individual capacitor.

Switches

Two or more switches in parallel, form a logical OR; the circuit carries current if at least one switch is 'on'. See OR gate.

Cells and batteries

If the cells of a battery are connected in parallel, the battery voltage will be the same as the cell voltage but the current supplied by each cell will be a fraction of the total current. For example, if a battery contains four cells connected in parallel and delivers a current of 1 ampere, the current supplied by each cell will be 0.25 ampere. Parallel-connected batteries were widely used to power the valve filaments in portable radios but they are now rare.

Applications

Series circuits were formerly used for lighting in electric multiple unit trains. For example, if the supply voltage was 600 volts there might be eight 70 volt bulbs in series (total 560 volts) plus a resistor to drop the remaining 40 volts. Series circuits for train lighting were superseded, first by motor-generators, then by solid state devices.

Series resistance can also be applied to the arrangement of blood vessels within a given organ. Each organ is supplied by a large artery, smaller arteries, arterioles, capillaries, and veins arranged in series. The total resistance is the sum of the individual resistances, as expressed by the following equation: R_total = R_artery + R_arterioles + R_capillaries. The largest proportion of resistance in this series is contributed by the arterioles.

Parallel resistance is illustrated by the system circulation. Each organ is supplied by an artery that branches off the aorta. The total resistance of this parallel arrangement is expressed by the following equation: 1/R_total = 1/R_a + 1/R_b + ... 1/R_n. R_a, R_b, and R_n are the resistances of the renal, hepatic, and other arteries respectively. The total resistance is less than the resistance of any of the individual arteries.

See also

• network analysis (electrical circuits)
• Wheatstone bridge
• Y-Δ transform
• Voltage divider
• Current divider
• Combining impedances
• Equivalent impedance transforms

References

• Resnick, Robert and Halliday, David (1966), Physics, Vol I and II, Combined edition, Wiley International Edition, Library of Congress Catalog Card No. 66-11527
• Smith, R.J. (1966), Circuits, Devices and Systems, Wiley International Edition, New York. Library of Congress Catalog Card No. 66-17612
• Williams, Tim, The Circuit Designer's Companion, Butterworth-Heinemann, 2005 ISBN 0750663707.

External links

• Calculators for resistors in series and parallel.
• What is a series-parallel circuit?
• Images for series parallel circuits
• Series circuits – see page 14 and onwards
• Parallel circuit – see page 22 and onwards