Guitar tunings

Guitar tunings assign pitches to the open strings of guitars. Tunings can be described by the particular pitches that are denoted by notes in Western music. By convention, the notes are ordered from lowest to highest.[1] This article describes the standard tuning used by the majority of guitarists, and also alternative tunings.
The phrase "guitar tuning" also refers to the adjusting of the string-pitches to their desired tuning, which is described in how-to manuals for guitarists.[2]
The standard tuning defines the string pitches as E, A, D, G, B, and E, from lowest (low E) to highest (high E). Standard tuning is used by most guitarists, and frequently used tunings can be understood as variations on standard tuning.
Nonstandard tunings are also called "alternative" or "alternate". Some tunings are used for particular songs by professional musicians, and may be called after the song's title. There are hundreds of such tunings, which are often minor variants of established tunings. Fewer alternative tunings are used regularly by communities of guitarists, who share a musical tradition.
The hundreds of alternative tunings have been classified into a smaller number of categories: open, both major and minor (crossnote), and modal; dropped; instrumental (based on other stringed instruments); and regular. Modal, dropped, and many other tunings are mentioned in the supplementary list of guitar tunings.
Standard and alternatives
This summary of standard tuning also introduces the terms for discussing alternative tunings
Standard
Guitar tunings have evolved over the years. Standard tuning is currently the most popular tuning on a 6-string guitar and in the music industry it is the assumed default if a specific tuning is not mentioned. It consists of the following notes:
- E-A-d-g-b-e'.
The exact pitch of the notes used in standard tuning and scientific pitch notation is used to differentiate the notes from different octaves [3]:
| String | Frequency | Scientific pitch notation |
|---|---|---|
| 1 (e) | 329.63 Hz | E4 |
| 2 (B) | 246.94 | B3 |
| 3 (G) | 196.00 | G3 |
| 4 (D) | 146.83 | D3 |
| 5 (A) | 110.00 | A2 |
| 6 (E) | 82.41 | E2 |
In regions of Europe where classical musicians use the German system, the B natural is indicated with the letter H: in music notation, H is B♮ (B natural), and B is B♭ (B flat). The guitar is a transposing instrument which transposes its notation one octave higher than its sounding pitches, to simplify notation.
The guitar, as conventionally fretted, is a mostly-equal-tempered instrument. The frets on each string create equal tempered pitches along each string. However, guitarists who tune by ear will typically tune the open strings "clean", or without tuning beats, so that the open strings are in tune according to the harmonic series, which is at variance with the equal tempered system. In this way, the guitar produces equal tempered pitches horizontally along strings, but is capable of producing some clean intervals across strings. The alternative tunings described below, especially those that tune the guitar to an open chord, will tune the strings cleanly so that the guitar will produce a similar combination of equal tempered and "clean" intervals.
Standard tuning provides simple fingering for many chords and the ability to play common scales with reasonable left-hand movement. The separation of the first (e') and second (b) string, as well as the separation between the third (g), fourth (d), fifth (A), and sixth (E) strings by a five-semitone interval (a perfect fourth) allows notes of the chromatic scale to be played with each of the four fingers of the left hand controlling one of the first four frets (index finger on fret 1, little finger on fret 4, etc.) only when the hand is in the first position; otherwise, the four fingers must stretch to cover five frets.
The separation of the second (b), and third (g) string is by a four-semitone interval (a major third). The irregular major-third provides B and E as open notes, which is convenient for many chords. On the other hand, the irregular major-third breaks the fingering patterns of scales and chords, so that guitarists have to memorize three-to-four chord-shapes for each chord. Scales and chords are simplified by major thirds tuning and all-fourths tuning, which are regular tunings maintaining the same musical interval between consecutive open-string notes.
| I | |||||
|---|---|---|---|---|---|
| open | 1st fret (index) | 2nd fret (middle) | 3rd fret (ring) | 4th fret (little) | |
| 1st string | e' | f' | f♯' | g' | a♭' |
| 2nd string | b | c' | c♯' | d' | e♭' |
| 3rd string | g | a♭ | a | b♭ | b |
| 4th string | d | e♭ | e | f | f♯ |
| 5th string | A | B♭ | B | c | c♯ |
| 6th string | E | F | F♯ | G | A♭ |
| Chromatic note progression | |||||
Alternative
Alternative ("alternate") tuning refers to any open-string note-arrangement other than standard tuning. Such alternative tuning arrangements offer different chord voicing and sonorities. Alternative tunings are common in folk music, where the guitar emulates indigenous instruments with distinct drones and sound. Alternative tunings necessarily change the chord shapes associated with standard tuning, which eases the playing of some non-standard chords at the cost of increasing the difficulty of some standard chords.
Some tunings are used for particular songs by professional musicians, and may be called after the song's title. There are hundreds of such tunings, which are often minor variants of established tunings.[4] Fewer alternative tunings are used regularly by communities of guitarists, who share a musical tradition, such as American folk or Celtic folk music.
The hundreds of alternative tunings have been classified into a smaller number of categories:[5] open,[6] both major and minor (cross note),[7][8][9] miscellaneous ("special"),[8][9][10] modal,[8][11] dropped,[12][8] instrumental (based on other stringed instruments), and regular.[9]
String gauges
Many alternative tunings are difficult or impossible with conventional sets of guitar strings, which have gauges optimized for standard tuning. With conventional sets, some higher tunings increase string-tension until playing requires more finger-strength and stamina or even until a string snaps or the guitar is warped; with lower tunings, strings may be loose and buzz. Therefore, many alternative tunings benefit from re-stringing of the guitar with different gauges.[13]
Open

An open tuning allows a chord to be played by strumming the strings when "open", or while fretting no strings. The base chord consists of at least three notes and may include all the strings or a subset. The tuning is named for the base chord when played open, typically a major chord, and all similar chords in the chromatic scale can then be played by barring exactly one fret.[14] Open tunings are common in blues and folk music,[15] and they are used in the playing of slide and lap-slide ("Hawaiian") guitars.[14][16] Ry Cooder uses open tunings when he plays slide guitar.[15]
Open tunings allow improved intonation of major chords than do non-open tunings, because open tunings reduce the error of thirds in equal temperaments tuning. For example, in the open-G overtones tuning G-G-D-G-B-D, the (G,B) interval is a major third, and of course each successive pair of notes on the G- and B-strings is also a major third; similarly, the open-string minor-third (B,D) induces minor thirds among all the frets of the B-D strings. Of all the intervals in equal temperament, the thirds have the largest error in comparison to those of just intonation: Equal temperaments is used in modern music because it facilitates music in all keys, while (on a piano and other instruments) just intonation provided better-sounding major-third intervals for only a subset of keys.[17] "Sonny Landreth, Keith Richards and other open-G masters often lower the second string slightly so the major third is in tune with the overtone series. This adjustment dials out the dissonance, and makes those big one-finger major-chords come alive."[18]
Relative to the "pure" thirds in the overtone series, equal-temperament widens the major third by an all-too audible 14 cents, and it narrows the minor third by an even more horrifying 16 cents (1 cent is one hundredth (1 percent) of a semitone). So, the 3 note (F#) of a D-major chord, and the b3 note (F) of a D-minor chord, may well sound a lot better / more pleasing to the ear if they are adjusted downward or upward, respectively. Unfortunately, making such an adjustment in standard tuning – and in most other tunings – is inadmissible, because it's not possible to tune the notes sounded on a particular string individually; adjusting the intonation of a string affects the intonation of all of the notes which lie "under" it ... some of which will be the 1, 4, and 5 notes of other chords. Since these notes are not displaced (or are only slightly displaced) by even-temperament, any adjustment to "improve" the intonation of a 3 note in one chord will just throw other chords badly out-of-tune.
Our "open" tunings (ones whose open strings form a simple chord) are the one exception to this rule. To the extent that we play with a slide (like the Delta blues players) or with one barred finger or some other grip (Keith Richards) that is essentially just moved up and down the neck, ... then the 3 of the chord can be tuned more or less "pure", as in the holy overtone series. In open-G tuning (G,G,D,G,B,D), the 3 (B) of the open-G major-triad is on string 2. If we barre or use a slide to play the IV chord (C) at fret 5, the 3 of that chord (E) is still on string 2 ... as it will be when we slide up to the V chord, or the bVII chord, or the octave. As long as we don't wantonly introduce other chord shapes, our adjustment to string 2 won't break anything. If we're playing with a slide, this is more or less guaranteed.[19]
— Warren Allen
Repetitive open-tunings are used for two classical non-Spanish guitars. For the English guitar, the open chord is C major (C-E-G-C-E-G);[20] for the Russian guitar which has seven strings, G major (G-B-D-G-B-D-G).[21] Mixing a perfect fourth and a minor third along with a major third, these tunings are on-average major-thirds regular-tunings. While on-average major-thirds tunings are conventional open tunings, properly major-thirds tunings are unconventional open-tunings, because they have augmented triads as their open chords.[22]
When the open strings constitute a minor chord, the open tuning is called a cross-note tuning.
Major


Major open-tunings give a major chord with the open strings.
| Major triad | Repetitive | Overtones | Other (often most popular) | |
|---|---|---|---|---|
| Open A | (A,C♯,E) | A-C♯-E-A-C♯-E | A-A-E-A-C♯-E | E-A-C♯-E-A-E |
| Open B | (B,D♯,F♯) | B-D♯-F♯-B-D♯-F♯ | B-B-F♯-B-D♯-F♯ | B-F♯-B-F♯-B-D♯ |
| Open C | (C,E,G) | C-E-G-C-E-G | C-C-G-C-E-G | C-G-C-G-C-E |
| Open D | (D,F♯,A) | D-F♯-A-D-F♯-A | D-D-A-D-F♯-A | D-A-D-F♯-A-D |
| Open E | (E,G♯,B) | E-G♯-B-E-G♯-B | E-E-B-E-G♯-B | E-B-E-G♯-B-E |
| Open F | (F,A,C) | F-A-C-F-A-C | F-F-C-F-A-C | C-F-C-F-A-F |
| Open G | (G,B,D) | G-B-D-G-B-D | G-G-D-G-B-D | D-G-D-G-B-D |
Open tunings often tune the lowest open-note to C, D, or E and they often tune the highest open-note to D or E; tuning down the open-string from E to D or C avoids the risk of breaking strings, which is associated with tuning up strings. The most popular open-tunings have the open-string patterns
- R-5-R-5-R-3 (Open C),
- R-5-R-3-5-R (Open D and E),
- 5-R-5-R-3-5 (Open G)
where R, 3, and 5 represent the major triad's root, major third, or perfect fifth. In these tunings, the root is repeated thrice or twice, and the perfect fifth twice or thrice; the major third once.[23] In repetitive open-tunings, the open major-triad's major third is doubled; in non-repetitive open-tunings, the major third is not doubled. A seventh chord is often played by omitting the highest perfect-fifth; when a perfect fifth or other notes are omitted from a chord, the major-third note is retained.
Open C
The English guitar used a repetitive open-C tuning (with distinct open-notes C-E-G-C-E-G) that approximated a major-thirds tuning.[24] The C-G-C-G-C-E tuning was used by William Ackerman for his "Townsend Shuffle" and by John Fahey for his tribute to Mississippi John Hurt.[25][26]
The C-C-G-C-E-G tuning uses the harmonic sequence (overtones) of the note C. When an open-note C-string is struck, its harmonic sequence begins with the notes (C,C,G,C,E,G,B♭,C).[27][28] This overtone-series tuning was modified by Mick Ralphs, who used a high C rather than the high G for "Can't get enough" on Bad Company. Ralphs said, "It needs the open C to have that ring," and "it never really sounds right in standard tuning". Ralphs wrote these songs in the key of G on a guitar in Open-G tuning.[29]
Another open-C tuning has the open notes C-G-C-G-C-E; it was used by William Ackerman for his "Townsend Shuffle" and by John Fahey for his tribute to Mississippi John Hurt. [30]
Open G
Mick Ralph's Open-C tuning was originally an open-G tuning, which listed the initial six overtones of the G note, namely G-G-D-G-B-D; Ralphs used this open-G tuning for "Hey Hey" and while writing the demo of "Can't Get Enough".[29] The open G tuning G-G-D-G-B-D was used by Joni Mitchell for "Electricity", "For the Roses", and "Hunter (The Good Samaritan)".[31] Truncating this tuning to G-D-G-B-D for his five-string guitar, Keith Richards plays this overtones-tuning on The Rolling Stones's "Honky Tonk Women", "Brown Sugar" and "Start Me Up".[32]
The Russian guitar uses the open-G tuning D-G-B-D-G-B-D, which is approximately in major thirds.[33][34]
Open D
An Open D tuning D-A-D-F♯-A-D was used by Joni Mitchell for her "Big Yellow Taxi" and by The Allman Brothers for their "Little Martha".[35] Open-D tuning has been called Vestopol tuning.[36]
Minor: Cross-note
Cross-note tunings use a minor third, so giving a minor chord with open strings. To avoid the relatively cumbersome designation "open D minor", "open C minor", such tunings are sometimes called "cross-note tunings". Fretting the minor-third string at the first fret produces a major-third, so allowing a one-finger fretting of a major chord.[37] It is more difficult to fret a minor chord using an open major-chord tuning.
Cross-note E-minor was used by Bukka White and Skip James.[38]
Regular
| Regular tunings | |
|---|---|
 For regular guitar-tunings, the distance between consecutive open-strings is a constant musical-interval, measured by semitones on the chromatic circle. The chromatic circle lists the twelve notes of the octave. | |
| Basic information | |
| Aliases | Uniform tunings |
| Advanced information | |
| Advantages | Simplifies learning by beginners and improvisation by advanced guitarists |
| Disadvantages | Replicating the open chords ("cowboy chords") of standard tuning is difficult; intermediate guitarists must relearn the fretboard and chords. |
| Regular tunings (semitones) | |
| Trivial (0) | |
| Minor thirds (3) | |
| Major thirds (4) | |
| All fourths (5) | |
| Augmented fourths (6) | |
| New standard (7, 3) | |
| All fifths (7) | |
| Minor sixths (8) | |
| Guitar tunings | |
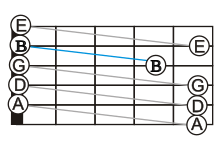
For the standard tuning, there is exactly one interval of a third between the second and third strings, and all the other intervals are fourths. The irregularity has a price. Chords cannot be shifted around the fretboard in the standard tuning E-A-D-G-B-E, which requires four chord-shapes for the major chords. There are separate chord-forms for chords having their root note on the third, fourth, fifth, and sixth strings.[39]
In contrast, regular tunings have equal intervals between the strings,[40] and so they have symmetrical scales all along the fretboard. This makes it simpler to translate chords. For the regular tunings, chords may be moved diagonally around the fretboard. The diagonal movement of chords is especially simple for the regular tunings that are repetitive, in which case chords can be moved vertically: Chords can be moved three strings up (or down) in major-thirds tuning and chords can be moved two strings up (or down) in augmented-fourths tuning. Regular tunings thus appeal to new guitarists and also to jazz-guitarists, whose improvisation is simplified by regular intervals.
On the other hand, 5-6 string open chords ("cowboy chords") are more difficult to play in a regular tuning than in standard tuning. Instructional literature uses standard tuning.[41] Traditionally a course begins with the hand in first position,[42] that is, with the left-hand covering frets 1–4.[43] Beginning players first learn open chords belonging to the major keys C, G, and D. Guitarists who play mainly open chords in these three major-keys and their relative minor-keys (Am, Em, Bm) may prefer standard tuning over many regular tunings,[44][45] On the other hand, minor-thirds tuning features many barre chords with repeated notes,[46] properties that appeal to acoustic-guitarists and beginners.
Major thirds and perfect fourths
Standard tuning mixes a major third (M3) with its perfect fourths. Regular tunings that are based on either major thirds or perfect fourths are used, for example, in jazz.
All fourths tuning E-A-d-g-c'-f' keeps the lowest four strings of standard tuning, changing the major third to a perfect fourth.[47][48] Jazz musician Stanley Jordan stated that all-fourths tuning "simplifies the fingerboard, making it logical".[49]
Major-thirds tuning (M3 tuning) is a regular tuning in which the musical intervals between successive strings are each major thirds, for example
Unlike all-fourths and all-fifths tuning, M3 tuning repeats its octave after three strings, which simplifies the learning of chords and improvisation.[41] This repetition provides the guitarist with many possibilities for fingering chords.[52][22] With six strings, major-thirds tuning has a smaller range than standard tuning; with seven strings, the major-thirds tuning covers the range of standard tuning on six strings.[52][50][51]
Major-thirds tunings require less hand-stretching than other tunings, because each M3 tuning packs the octave's twelve notes into four consecutive frets.[50][53] The major-third intervals allow major chords and minor chords to be played with two–three consecutive fingers on two consecutive frets.[54]
Chord inversion is especially simple in major-thirds tuning. Chords are inverted simply by raising one or two notes three strings. The raised notes are played with the same finger as the original notes. In contrast, inversions of triads in standard and all-fourths tuning require three fingers on a span of four frets,[55] in standard tuning, the shape of inversions depends on the involvement of the irregular major-third.[56]
All fifths and new standard tuning

- C-G-d-a-e'-b'
All-fifths tuning is a tuning in intervals of perfect fifths like that of a mandolin or a violin; other names include "perfect fifths" and "fifths".[57] It has a wide range. Its implementation has been impossible with nylon strings and has been difficult with conventional steel strings. The high b makes the first string very taut, and consequently a conventionally gauged string would easily break.
All-fifths tuning has been approximated by the New Standard Tuning (NST) of King Crimson's Robert Fripp, which NST replaces all-fifth's high b' with a g'. To build chords, Fripp uses "perfect intervals in fourths, fifths and octaves", so avoiding minor thirds and especially major thirds,[58] which are sharp in equal temperament tuning (in comparison to thirds in just intonation). It is a challenge to adapt conventional guitar-chords to new standard tuning, which is based on all-fifths tuning.[59] Some closely voiced jazz chords become impractical in NST and all-fifths tuning.[60]
Other tunings
This article has discussed the main classes of guitar tunings which have been described in reliable sources. Many examples of alternative tunings, such as open and regular tunings, appear in the supplementary list of guitar tunings. This extensive list also has sections on "dropped" tunings and tunings associated with instruments other than guitars. The list also includes ad-hoc tunings, often associated with a particular piece (song and music).
See also
Notes
- ^ Denyer. Chapter "Playing the guitar": 'How the guitar is tuned', pp. 68-69.
- ^ Denyer. Chapter "Playing the guitar": 'Tuning methods', pp. 70-71.
- ^ Online guitar tuner “Retrieved August 27, 2013”
- ^ Weissman (2006, Off the wall tunings: A brief inventory (Appendix A), pp. 95-96)
- ^ Roche (2004, "Categories of tunings", p. 153)
- ^ Roche (2004, "Open tunings", pp. 156–159)
- ^ Roche (2004, "Cross-note tunings", p. 166)
- ^ a b c d Denyer (1992, pp. 158–159)
- ^ a b c Sethares (2011)
- ^ Roche (2004, "More radical tunings", p. 166)
- ^ Roche (2004, "Modal tunings", pp. 160–165)
- ^ Roche (2004, pp. 153–156)
- ^ Roche (2004, "String gauges and altered tunings", p. 169–170)
- ^ a b Sethares (2009, p. 16)
- ^ a b Denyer (1992, p. 158)
- ^ Denyer (1992, p. 160)
- ^ Gold, Jude (2005). "Just desserts: Steve Kimock shares the sweet sounds of justly tuned thirds and sevenths". Guitar Player. Master class.
{{cite journal}}: Cite has empty unknown parameter:|1=(help); Invalid|ref=harv(help); Unknown parameter|month=ignored (help) (subscription required) - ^ Template:Cite article
- ^ Allen (2011) harvtxt error: multiple targets (2×): CITEREFAllen2011 (help)
- ^ "Composers for other plucked instruments: Rudolf Straube (1717-1785)". Handbook of Guitar and Lute Composers (Translated by
Katarina Backman ed.). Mel Bay. 2007. p. 30. ISBN 0786658444; ISBN 9780786658442.
{{cite book}}: Cite has empty unknown parameter:|1=(help); Invalid|ref=harv(help); Unknown parameter|authors=ignored (help); line feed character in|edition=at position 14 (help) - ^
- Ophee, Matanya (ed.). 19th Century etudes for the Russian 7-string guitar in G Op. The Russian Collection. Vol. 9. Editions Orphee. PR.494028230.
{{cite book}}: Invalid|ref=harv(help) - Ophee, Matanya (ed.). Selected Concert Works for the Russian 7-String Guitar in G open tuning. The Russian Collection. Vol. 10 ("X"). Editions Orphee. PR.494028240.
{{cite book}}: Invalid|ref=harv(help) - Timofeyev, Oleg V. (1999). The golden age of the Russian guitar: Repertoire, performance practice, and social function of the Russian seven-string guitar music, 1800-1850. Duke University, Department of Music. pp. 1–584. University Microfilms (UMI), Ann Arbor, Michigan, number 9928880.
{{cite book}}: Invalid|ref=harv(help)
- Ophee, Matanya (ed.). 19th Century etudes for the Russian 7-string guitar in G Op. The Russian Collection. Vol. 9. Editions Orphee. PR.494028230.
- ^ a b c Sethares (2001, pp. 56)
- ^ Denyer (1992, p. 158)
- ^ "Composers for other plucked instruments: Rudolf Straube (1717-1785)". Handbook of guitar and lute composers (Translated by
Katarina Backman ed.). Mel Bay. 2007. p. 30. ISBN 0786658444. ISBN 9780786658442.
{{cite book}}: Invalid|ref=harv(help); Unknown parameter|authors=ignored (help); line feed character in|edition=at position 14 (help) - ^ Sethares (2009, pp. 18–19)
- ^ Baughman, Steve (2004). "Open C". Mel Bay Beginning Open Tunings. Pacific, Missouri: Mel Bay Publications. pp. 8–14. ISBN 978-0-7866-7093-2.
{{cite book}}: External link in|chapterurl=|chapterurl=ignored (|chapter-url=suggested) (help) - ^ Guitar Tunings Database (2013). "CCGCEG Guitar Tuner". CCGCEG: Open C via harmonic overtones. Retrieved 20 February 2013.
{{cite web}}: Check date values in:|accessdate=(help); Invalid|ref=harv(help) - ^ Persichetti (1961, pp. 23–24): Persichetti, Vincent (1961). Twentieth-century harmony: Creative aspects and practice. New York: W. W. Norton. ISBN 0-393-09539-8. OCLC 398434.
{{cite book}}: Invalid|ref=harv(help) - ^ a b Sharken, Lisa (2001). "Mick Ralphs: The rock 'N' roll fantasy continues". Vintage Guitar. Retrieved 21 February 2013.
{{cite journal}}: Cite has empty unknown parameter:|1=(help); Invalid|ref=harv(help); Unknown parameter|month=ignored (help) - ^ Sethares (2009, pp. 18–19)
- ^ "List of all Guitar and Piano Transcriptions". GGDGBD. JoniMitchell.com. Retrieved February 22, 2013.
- ^ Ellis, Andy (2005). "How to play like ... Keith Richards". Guitar Player. (subscription required). Retrieved 24 March 2013.
{{cite journal}}: Cite has empty unknown parameter:|1=(help); Invalid|ref=harv(help) - ^ Bellow (1970, p. 164): Bellow, Alexander (1970). The illustrated history of the guitar. Colombo Publications.
{{cite book}}: Invalid|ref=harv(help) - ^ Timofeyev (1999) harvtxt error: multiple targets (2×): CITEREFTimofeyev1999 (help): Timofeyev, Oleg V. (1999). The golden age of the Russian guitar: Repertoire, performance practice, and social function of the Russian seven-string guitar music, 1800-1850. Duke University, Department of Music. pp. 1–584. University Microfilms (UMI), Ann Arbor, Michigan, number 9928880.
{{cite book}}: Invalid|ref=harv(help) - ^ Sethares (2009, pp. 20–21)
- ^ Grossman (1972, p. 29)
- ^ Sethares (2001, p. 16)
- ^ Cohen, Andy (22 March 2005). "Stefan Grossman- Country Blues Guitar in Open Tunings". Sing Out!. 49 (1): 152.
- ^ Denyer (1992, p. 119)
- ^ Sethares (2001, p. 52)
- ^ a b Kirkeby, Ole (2012). "Major thirds tuning". m3guitar.com. cited by Sethares (2011). Retrieved 10 June 2012.
{{cite web}}: Cite has empty unknown parameter:|1=(help); Invalid|ref=harv(help); Unknown parameter|month=ignored (help) - ^ White, Mark (2005). "Reading skills: The guitarist's nemesis?". Berklee Today. 72. Boston, Massachusetts: Berklee College of Music. ISSN 1052-3839.
{{cite journal}}: Cite has empty unknown parameter:|1=(help); External link in|journal=|ref=harv(help) - ^ Denyer (1992, p. 72)
- ^ Peterson (2002, p. 37)
- ^ Griewank (2010, p. 5)
- ^ Sethares & 54–55
- ^ Sethares (2001, pp. 58–59)
- ^ Bianco, Bob (1987). Guitar in Fourths. New York City: Calliope Music. ISBN 0-9605912-2-2. OCLC 16526869.
- ^
Ferguson (1986, p. 76):
Ferguson, Jim (1986). "Stanley Jordan". In Casabona, Helen; Belew, Adrian (eds.). New directions in modern guitar. Guitar Player basic library. Hal Leonard Publishing Corporation. pp. 68–76. ISBN 0881884235; ISBN 9780881884234.{{cite book}}: Invalid|ref=harv(help) - ^ a b c Peterson (2002, pp. 36–37)
- ^ a b Griewank (2010)
- ^ a b c Patt, Ralph (2008). "The major 3rd tuning". Ralph Patt's jazz web page. ralphpatt.com. cited by Sethares (2011). Retrieved 10 June 2012.
{{cite web}}: Check date values in:|accessdate=(help); Cite has empty unknown parameter:|1=(help); Invalid|ref=harv(help); Unknown parameter|month=ignored (help) - ^ Griewank (2010, p. 9)
- ^ Griewank (2010, p. 2)
- ^ Griewank (2010, p. 10)
- ^ Denyer (1992, p. 121)
- ^ Sethares (2001, "The mandoguitar tuning" 62–63)
- ^ Mulhern (1986): Mulhern, Tom (1986). "On the discipline of craft and art: An interview with Robert Fripp". Guitar Player. 20: 88–103. Retrieved 8 January 2013.
{{cite journal}}: Invalid|ref=harv(help); Unknown parameter|month=ignored (help) - ^ Musicologist Eric Tamm wrote that despite "considerable effort and search I just could not find a good set of chords whose sound I liked" for rhythm guitar. (Tamm 2003, Chapter 10: Postscript)
Tamm, Eric (2003) [1990], Robert Fripp: From crimson king to crafty master (Progressive Ears ed.), Faber and Faber (1990), ISBN 0-571-16289-4, Zipped Microsoft Word Document, retrieved 25 March 2012{{citation}}: Invalid|ref=harv(help) - ^ Sethares (2001, "The mandoguitar tuning", pp. 62–63)
References
- Allen, Warren (2011) [30 December 1997]. "WA's encyclopedia of guitar tunings". (Recommended by Marcus, Gary (2012). Guitar zero: The science of learning to be musical. Oneworld. p. 234. ISBN 9781851689323.). Retrieved 27 June 2012.
{{cite web}}: Cite has empty unknown parameter:|1=(help); Invalid|ref=harv(help); Unknown parameter|month=ignored (help) - Denyer, Ralph (1992). "Playing the guitar ('How the guitar is tuned', pp. 68–69, and 'Alternative tunings', pp. 158–159)". The guitar handbook. Special contributors Isaac Guillory and Alastair M. Crawford (Fully revised and updated ed.). London and Syndey: Pan Books. pp. 65–160. ISBN 0-330-32750-X.
- Griewank, Andreas (2010), Tuning guitars and reading music in major thirds, Matheon preprints, vol. 695, Rosestr. 3a, 12524 Berlin, Germany: DFG research center "MATHEON, Mathematics for key technologies" Berlin, urn:nbn:de:0296-matheon-6755. Postscript file and Pdf file
{{citation}}: Cite has empty unknown parameter:|1=(help); Invalid|ref=harv(help); Unknown parameter|month=ignored (help)CS1 maint: location (link) - Grossman, Stefan (1972). The book of guitar tunings. New York: Amsco Publishing Company. ISBN 0-8256-2806-7. LCCN 74-170019.
{{cite book}}: Invalid|ref=harv(help) - Peterson, Jonathon (2002). "Tuning in thirds: A new approach to playing leads to a new kind of guitar". American Lutherie: The Quarterly Journal of the Guild of American Luthiers. 72 (Winter). 8222 South Park Avenue, Tacoma WA 98408: USA.: The Guild of American Luthiers: 36–43. ISSN 1041-7176.
{{cite journal}}: CS1 maint: location (link) - Roche, Eric (2004). "5 Thinking outside the box". The acoustic guitar Bible. London: Bobcat Books Limited, SMT. pp. 151–178. ISBN 1-84492-063-1.
{{cite book}}: Invalid|ref=harv(help) - Sethares, Bill (2001). "Regular tunings". Alternate tuning guide (pdf). Madison, Wisconsin: University of Wisconsin; Department of Electrical Engineering. pp. 52–67. Retrieved 19 May 2012.
{{cite book}}: Invalid|ref=harv(help) - Sethares, Bill (2009) [2001]. Alternate tuning guide (pdf). Madison, Wisconsin: University of Wisconsin; Department of Electrical Engineering. Retrieved 19 May 2012.
{{cite book}}: Invalid|ref=harv(help) - Sethares, William A. (2011). "Alternate tuning guide". Madison, Wisconsin: University of Wisconsin; Department of Electrical Engineering. Retrieved 19 May 2012.
{{cite web}}: Check date values in:|accessdate=(help); Invalid|ref=harv(help) - Weissman, Dick (2006). Guitar tunings: A comprehensive guide. Routledge. ISBN 9780415974417. LCCN 0415974410.
{{cite book}}: Invalid|ref=harv(help)
Further reading
- Anonymous (2000). Alternate tunings guitar essentials. Acoustic Guitar Magazine's private lessons. String Letter Publishing. Hal Leonard Publishing Corporation. ISBN 9781890490249. LCCN 1890490245.
{{cite book}}: Invalid|ref=harv(help) - Hanson, Mark (1995). The complete book of alternate tunings. Accent on Music. ISBN 9780936799131.
{{cite book}}: Invalid|ref=harv(help) - Hanson, Mark (1997). Alternate tunings picture chords. Accent on Music. ISBN 9780936799148. LCCN 0936799145.
{{cite book}}: Invalid|ref=harv(help) - Heines, Danny (2007). Mastering alternate tunings: A revolutionary system of fretboard navigation for fingerstyle guitarists. Hal Leonard. ISBN 9780634065699. LCCN 0634065696.
{{cite book}}: Invalid|ref=harv(help) - Johnson, Chad (2002). Alternate tuning chord dictionary. Hal Leonard. ISBN 9780634038570. LCCN 2005561612.
{{cite book}}: Invalid|ref=harv(help) - Maloof, Richard (2007). Alternate tunings for guitar. Cherry Lane Music Company. ISBN 1575605783. LCCN 9781575605784.
{{cite book}}: Check|lccn=value (help); Invalid|ref=harv(help) - Shark, Mark (2008). The tao of tunings: A map to the world of alternate tunings. Hal Leonard Corporation. ISBN 9781423430872. LCCN 1423430875.
{{cite book}}: Invalid|ref=harv(help)
External links
- Allen, Warren (2011) [30 December 1997]. "WA's encyclopedia of guitar tunings". (Recommended by Marcus, Gary (2012). Guitar zero: The science of learning to be musical. Oneworld. p. 234. ISBN 9781851689323.). Retrieved 27 June 2012.
{{cite web}}: Cite has empty unknown parameter:|1=(help); Invalid|ref=harv(help); Unknown parameter|month=ignored (help)
- Sethares, William A. (2012). "Alternate tuning guide: Interactive". Uses Wolfram Cdf player. Retrieved 27 June 2012.
{{cite web}}: Invalid|ref=harv(help); Unknown parameter|month=ignored (help)


