Bicupola
| Set of bicupolae | |
|---|---|
 Examples: Triangular gyrobicupola | |
| Faces | 2n triangles, 2n squares 2 n-gons |
| Edges | 8n |
| Vertices | 4n |
| Symmetry group | Ortho: Dnh, [2,n], *n22, order 4n Gyro: Dnd, [2+,2n], 2*n, order 4n |
| Properties | convex |
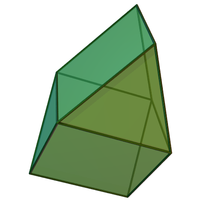
In geometry, a bicupola is a solid formed by connecting two cupolae on their bases.
There are two classes of bicupola because each cupola half is bordered by alternating triangles and squares. If similar faces are attached together the result is an orthobicupola; if squares are attached to triangles it is a gyrobicupola.
Cupolae and bicupolae categorically exist as infinite sets of polyhedra, just like the pyramids, bipyramids, prisms, and trapezohedra.
Six bicupolae have regular polygon faces: triangular, square and pentagonal ortho- and gyrobicupolae. The triangular gyrobicupola is an Archimedean solid, the cuboctahedron; the other five are Johnson solids.
Bicupolae of higher order can be constructed if the flank faces are allowed to stretch into rectangles and isosceles triangles.
Bicupolae are special in having four faces on every vertex. This means that their dual polyhedra will have all quadrilateral faces. The best known example is the rhombic dodecahedron composed of 12 rhombic faces. The dual of the ortho-form, triangular orthobicupola, is also a dodecahedron, similar to rhombic dodecahedron, but it has 6 trapezoid faces which alternate long and short edges around the circumference.
Forms
Set of orthobicupolae
| Symmetry | Picture | Description |
|---|---|---|
| D2h [2,2] *222 |

|
Orthobifastigium or digonal orthobicupola: 4 triangles (coplanar), 4 squares. It is self-dual |
| D3h [2,3] *223 |

|
Triangular orthobicupola (J27): 8 triangles, 6 squares; its dual is the trapezo-rhombic dodecahedron |
| D4h [2,4] *224 |

|
Square orthobicupola (J28): 8 triangles, 10 squares |
| D5h [2,5] *225 |

|
Pentagonal orthobicupola (J30): 10 triangles, 10 squares, 2 pentagons |
| Dnh [2,n] *22n |
n-gonal orthobicupola: 2n triangles, 2n rectangles, 2 n-gons |
Set of gyrobicupolae
A n-gonal gyrobicupola has the same topology as a n-gonal rectified antiprism, Conway polyhedron notation, aAn.
| Symmetry | Picture | Description |
|---|---|---|
| D2d [2+,4] 2*2 |

|
Gyrobifastigium (J26) or digonal gyrobicupola: 4 triangles, 4 squares |
| D3d [2+,6] 2*3 |

|
Triangular gyrobicupola or cuboctahedron: 8 triangles, 6 squares; its dual is the rhombic dodecahedron |
| D4d [2+,8] 2*4 |

|
Square gyrobicupola (J29): 8 triangles, 10 squares |
| D5d [2+,10] 2*5 |
Pentagonal gyrobicupola (J31): 10 triangles, 10 squares, 2 pentagons; its dual is the rhombic icosahedron | |
| Dnd [2+,2n] 2*n |
n-gonal gyrobicupola: 2n triangles, 2n rectangles, 2 n-gons |
References
- Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- Victor A. Zalgaller (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN. The first proof that there are only 92 Johnson solids.
