Neural network (machine learning)
It has been suggested that Neural network be merged into this article. (Discuss) Proposed since November 2008. |
This article needs additional citations for verification. (March 2009) |
An artificial neural network (ANN), usually called "neural network" (NN), is a mathematical model or computational model that tries to simulate the structure and/or functional aspects of biological neural networks. It consists of an interconnected group of artificial neurons and processes information using a connectionist approach to computation. In most cases an ANN is an adaptive system that changes its structure based on external or internal information that flows through the network during the learning phase. Modern neural networks are non-linear statistical data modeling tools. They are usually used to model complex relationships between inputs and outputs or to find patterns in data.

Background
There is no precise agreed-upon definition among researchers as to what a neural network is, but most would agree that it involves a network of simple processing elements (neurons), which can exhibit complex global behavior, determined by the connections between the processing elements and element parameters. The original inspiration for the technique came from examination of the central nervous system and the neurons (and their axons, dendrites and synapses) which constitute one of its most significant information processing elements (see neuroscience). In a neural network model, simple nodes, called variously "neurons", "neurodes", "PEs" ("processing elements") or "units", are connected together to form a network of nodes — hence the term "neural network". While a neural network does not have to be adaptive per se, its practical use comes with algorithms designed to alter the strength (weights) of the connections in the network to produce a desired signal flow.
These networks are also similar to the biological neural networks in the sense that functions are performed collectively and in parallel by the units, rather than there being a clear delineation of subtasks to which various units are assigned (see also connectionism). Currently, the term Artificial Neural Network (ANN) tends to refer mostly to neural network models employed in statistics, cognitive psychology and artificial intelligence. Neural network models designed with emulation of the central nervous system (CNS) in mind are a subject of theoretical neuroscience (computational neuroscience).
In modern software implementations of artificial neural networks the approach inspired by biology has for the most part been abandoned for a more practical approach based on statistics and signal processing. In some of these systems, neural networks or parts of neural networks (such as artificial neurons) are used as components in larger systems that combine both adaptive and non-adaptive elements. While the more general approach of such adaptive systems is more suitable for real-world problem solving, it has far less to do with the traditional artificial intelligence connectionist models. What they do have in common, however, is the principle of non-linear, distributed, parallel and local processing and adaptation.
Models
Neural network models in artificial intelligence are usually referred to as artificial neural networks (ANNs); these are essentially simple mathematical models defining a function . Each type of ANN model corresponds to a class of such functions.
The network in artificial neural network
The word network in the term 'artificial neural network' arises because the function is defined as a composition of other functions , which can further be defined as a composition of other functions. This can be conveniently represented as a network structure, with arrows depicting the dependencies between variables. A widely used type of composition is the nonlinear weighted sum, where , where (commonly referred to as the activation function[1]) is some predefined function, such as the hyperbolic tangent. It will be convenient for the following to refer to a collection of functions as simply a vector .

This figure depicts such a decomposition of , with dependencies between variables indicated by arrows. These can be interpreted in two ways.
The first view is the functional view: the input is transformed into a 3-dimensional vector , which is then transformed into a 2-dimensional vector , which is finally transformed into . This view is most commonly encountered in the context of optimization.
The second view is the probabilistic view: the random variable depends upon the random variable , which depends upon , which depends upon the random variable . This view is most commonly encountered in the context of graphical models.
The two views are largely equivalent. In either case, for this particular network architecture, the components of individual layers are independent of each other (e.g., the components of are independent of each other given their input ). This naturally enables a degree of parallelism in the implementation.

Networks such as the previous one are commonly called feedforward, because their graph is a directed acyclic graph. Networks with cycles are commonly called recurrent. Such networks are commonly depicted in the manner shown at the top of the figure, where is shown as being dependent upon itself. However, there is an implied temporal dependence which is not shown.
Learning
What has attracted the most interest in neural networks is the possibility of learning. Given a specific task to solve, and a class of functions , learning means using a set of observations to find which solves the task in some optimal sense.
This entails defining a cost function such that, for the optimal solution , (i.e., no solution has a cost less than the cost of the optimal solution).
The cost function is an important concept in learning, as it is a measure of how far away a particular solution is from an optimal solution to the problem to be solved. Learning algorithms search through the solution space to find a function that has the smallest possible cost.
For applications where the solution is dependent on some data, the cost must necessarily be a function of the observations, otherwise we would not be modelling anything related to the data. It is frequently defined as a statistic to which only approximations can be made. As a simple example consider the problem of finding the model which minimizes , for data pairs drawn from some distribution . In practical situations we would only have samples from and thus, for the above example, we would only minimize . Thus, the cost is minimized over a sample of the data rather than the entire data set.
When some form of online machine learning must be used, where the cost is partially minimized as each new example is seen. While online machine learning is often used when is fixed, it is most useful in the case where the distribution changes slowly over time. In neural network methods, some form of online machine learning is frequently used for finite datasets.
Choosing a cost function
While it is possible to define some arbitrary, ad hoc cost function, frequently a particular cost will be used, either because it has desirable properties (such as convexity) or because it arises naturally from a particular formulation of the problem (e.g., in a probabilistic formulation the posterior probability of the model can be used as an inverse cost). Ultimately, the cost function will depend on the task we wish to perform. The three main categories of learning tasks are overviewed below.
Learning paradigms
There are three major learning paradigms, each corresponding to a particular abstract learning task. These are supervised learning, unsupervised learning and reinforcement learning. Usually any given type of network architecture can be employed in any of those tasks.
Supervised learning
In supervised learning, we are given a set of example pairs and the aim is to find a function in the allowed class of functions that matches the examples. In other words, we wish to infer the mapping implied by the data; the cost function is related to the mismatch between our mapping and the data and it implicitly contains prior knowledge about the problem domain.
A commonly used cost is the mean-squared error which tries to minimize the average squared error between the network's output, f(x), and the target value y over all the example pairs. When one tries to minimize this cost using gradient descent for the class of neural networks called Multi-Layer Perceptrons, one obtains the common and well-known backpropagation algorithm for training neural networks.
Tasks that fall within the paradigm of supervised learning are pattern recognition (also known as classification) and regression (also known as function approximation). The supervised learning paradigm is also applicable to sequential data (e.g., for speech and gesture recognition). This can be thought of as learning with a "teacher," in the form of a function that provides continuous feedback on the quality of solutions obtained thus far.
Unsupervised learning
In unsupervised learning we are given some data and the cost function to be minimized, that can be any function of the data and the network's output, .
The cost function is dependent on the task (what we are trying to model) and our a priori assumptions (the implicit properties of our model, its parameters and the observed variables).
As a trivial example, consider the model , where is a constant and the cost . Minimizing this cost will give us a value of that is equal to the mean of the data. The cost function can be much more complicated. Its form depends on the application: for example, in compression it could be related to the mutual information between x and y, whereas in statistical modelling, it could be related to the posterior probability of the model given the data. (Note that in both of those examples those quantities would be maximized rather than minimized).
Tasks that fall within the paradigm of unsupervised learning are in general estimation problems; the applications include clustering, the estimation of statistical distributions, compression and filtering.
Reinforcement learning
In reinforcement learning, data are usually not given, but generated by an agent's interactions with the environment. At each point in time , the agent performs an action and the environment generates an observation and an instantaneous cost , according to some (usually unknown) dynamics. The aim is to discover a policy for selecting actions that minimizes some measure of a long-term cost; i.e., the expected cumulative cost. The environment's dynamics and the long-term cost for each policy are usually unknown, but can be estimated.
More formally, the environment is modeled as a Markov decision process (MDP) with states and actions with the following probability distributions: the instantaneous cost distribution , the observation distribution and the transition , while a policy is defined as conditional distribution over actions given the observations. Taken together, the two define a Markov chain (MC). The aim is to discover the policy that minimizes the cost; i.e., the MC for which the cost is minimal.
ANNs are frequently used in reinforcement learning as part of the overall algorithm.
Tasks that fall within the paradigm of reinforcement learning are control problems, games and other sequential decision making tasks.
See also: dynamic programming, stochastic control
Learning algorithms
Training a neural network model essentially means selecting one model from the set of allowed models (or, in a Bayesian framework, determining a distribution over the set of allowed models) that minimizes the cost criterion. There are numerous algorithms available for training neural network models; most of them can be viewed as a straightforward application of optimization theory and statistical estimation.
Most of the algorithms used in training artificial neural networks employ some form of gradient descent. This is done by simply taking the derivative of the cost function with respect to the network parameters and then changing those parameters in a gradient-related direction.
Evolutionary methods, simulated annealing, expectation-maximization and non-parametric methods are some commonly used methods for training neural networks. See also machine learning.
Temporal perceptual learning relies on finding temporal relationships in sensory signal streams. In an environment, statistically salient temporal correlations can be found by monitoring the arrival times of sensory signals. This is done by the perceptual network.
Employing artificial neural networks
Perhaps the greatest advantage of ANNs is their ability to be used as an arbitrary function approximation mechanism which 'learns' from observed data. However, using them is not so straightforward and a relatively good understanding of the underlying theory is essential.
- Choice of model: This will depend on the data representation and the application. Overly complex models tend to lead to problems with learning.
- Learning algorithm: There are numerous tradeoffs between learning algorithms. Almost any algorithm will work well with the correct hyperparameters for training on a particular fixed dataset. However selecting and tuning an algorithm for training on unseen data requires a significant amount of experimentation.
- Robustness: If the model, cost function and learning algorithm are selected appropriately the resulting ANN can be extremely robust.
With the correct implementation ANNs can be used naturally in online learning and large dataset applications. Their simple implementation and the existence of mostly local dependencies exhibited in the structure allows for fast, parallel implementations in hardware.
Applications
The utility of artificial neural network models lies in the fact that they can be used to infer a function from observations. This is particularly useful in applications where the complexity of the data or task makes the design of such a function by hand impractical.
Real life applications
The tasks to which artificial neural networks are applied tend to fall within the following broad categories:
- Function approximation, or regression analysis, including time series prediction, fitness approximation and modeling.
- Classification, including pattern and sequence recognition, novelty detection and sequential decision making.
- Data processing, including filtering, clustering, blind source separation and compression.
- Robotics, including directing manipulators, Computer numerical control.
Application areas include system identification and control (vehicle control, process control), quantum chemistry,[2] game-playing and decision making (backgammon, chess, racing), pattern recognition (radar systems, face identification, object recognition and more), sequence recognition (gesture, speech, handwritten text recognition), medical diagnosis, financial applications (automated trading systems), data mining (or knowledge discovery in databases, "KDD"), visualization and e-mail spam filtering.
Neural network software
Neural network software is used to simulate, research, develop and apply artificial neural networks, biological neural networks and in some cases a wider array of adaptive systems.
Types of neural networks
It has been suggested that this article be split into a new article titled Types of neural networks. (discuss) (August 2009) |
Feedforward neural network
The feedforward neural network was the first and arguably simplest type of artificial neural network devised. In this network, the information moves in only one direction, forward, from the input nodes, through the hidden nodes (if any) and to the output nodes. There are no cycles or loops in the network.
Radial basis function (RBF) network
Radial Basis Functions are powerful techniques for interpolation in multidimensional space. A RBF is a function which has built into a distance criterion with respect to a center. Radial basis functions have been applied in the area of neural networks where they may be used as a replacement for the sigmoidal hidden layer transfer characteristic in Multi-Layer Perceptrons. RBF networks have two layers of processing: In the first, input is mapped onto each RBF in the 'hidden' layer. The RBF chosen is usually a Gaussian. In regression problems the output layer is then a linear combination of hidden layer values representing mean predicted output. The interpretation of this output layer value is the same as a regression model in statistics. In classification problems the output layer is typically a sigmoid function of a linear combination of hidden layer values, representing a posterior probability. Performance in both cases is often improved by shrinkage techniques, known as ridge regression in classical statistics and known to correspond to a prior belief in small parameter values (and therefore smooth output functions) in a Bayesian framework.
RBF networks have the advantage of not suffering from local minima in the same way as Multi-Layer Perceptrons. This is because the only parameters that are adjusted in the learning process are the linear mapping from hidden layer to output layer. Linearity ensures that the error surface is quadratic and therefore has a single easily found minimum. In regression problems this can be found in one matrix operation. In classification problems the fixed non-linearity introduced by the sigmoid output function is most efficiently dealt with using iteratively re-weighted least squares.
RBF networks have the disadvantage of requiring good coverage of the input space by radial basis functions. RBF centres are determined with reference to the distribution of the input data, but without reference to the prediction task. As a result, representational resources may be wasted on areas of the input space that are irrelevant to the learning task. A common solution is to associate each data point with its own centre, although this can make the linear system to be solved in the final layer rather large, and requires shrinkage techniques to avoid overfitting.
Associating each input datum with an RBF leads naturally to kernel methods such as Support Vector Machines and Gaussian Processes (the RBF is the kernel function). All three approaches use a non-linear kernel function to project the input data into a space where the learning problem can be solved using a linear model. Like Gaussian Processes, and unlike SVMs, RBF networks are typically trained in a Maximum Likelihood framework by maximizing the probability (minimizing the error) of the data under the model. SVMs take a different approach to avoiding overfitting by maximizing instead a margin. RBF networks are outperformed in most classification applications by SVMs. In regression applications they can be competitive when the dimensionality of the input space is relatively small.
Kohonen self-organizing network
The self-organizing map (SOM) invented by Teuvo Kohonen performs a form of unsupervised learning. A set of artificial neurons learn to map points in an input space to coordinates in an output space. The input space can have different dimensions and topology from the output space, and the SOM will attempt to preserve these.
Recurrent network
Contrary to feedforward networks, recurrent neural networks (RNNs) are models with bi-directional data flow. While a feedforward network propagates data linearly from input to output, RNNs also propagate data from later processing stages to earlier stages. RNNs can be used as general sequence processors.
Fully recurrent network
This is the basic architecture developed in the 1980s: a network of neuron-like units, each with a directed connection to every other unit. Each unit has a time-varying real-valued activation. Each connection has a modifiable real-valued weight. Some of the nodes are called input nodes, some output nodes, the rest hidden nodes. Most architectures below are special cases.
For supervised learning in discrete time settings, training sequences of real-valued input vectors become sequences of activations of the input nodes, one input vector at a time. At any given time step, each non-input unit computes its current activation as a nonlinear function of the weighted sum of the activations of all units from which it receives connections. There may be teacher-given target activations for some of the output units at certain time steps. For example, if the input sequence is a speech signal corresponding to a spoken digit, the final target output at the end of the sequence may be a label classifying the digit. For each sequence, its error is the sum of the deviations of all target signals from the corresponding activations computed by the network. For a training set of numerous sequences, the total error is the sum of the errors of all individual sequences.
To minimize total error, gradient descent can be used to change each weight in proportion to its derivative with respect to the error, provided the non-linear activation functions are differentiable. Various methods for doing so were developed in the 1980s and early 1990s by Paul Werbos, Ron Williams, Tony Robinson, Jürgen Schmidhuber, Barak Pearlmutter, and others. The standard method is called "backpropagation through time" or BPTT, a generalization of back-propagation for feed-forward networks[3][4]. A more computationally expensive online variant is called "Real-Time Recurrent Learning" or RTRL[5][6]. Unlike BPTT this algorithm is local in time but not local in space[7][8]. There also is an online hybrid between BPTT and RTRL with intermediate complexity[9][10], and there are variants for continuous time[11]. A major problem with gradient descent for standard RNN architectures is that error gradients vanish exponentially quickly with the size of the time lag between important events, as first realized by Sepp Hochreiter in 1991[12][13]. The Long short term memory architecture overcomes these problems[14].
In reinforcement learning settings, there is no teacher providing target signals for the RNN, instead a fitness function or reward function or utility function is occasionally used to evaluate the performance of the RNN, which is influencing its input stream through output units connected to actuators affecting the environment. Variants of evolutionary computation are often used to optimize the weight matrix.
Hopfield network
The Hopfield network (like similar attractor-based networks) is of historic interest although it is not a general RNN, as it is not designed to process sequences of patterns. Instead it requires stationary inputs. It is a RNN in which all connections are symmetric. Invented by John Hopfield in 1982, it guarantees that its dynamics will converge. If the connections are trained using Hebbian learning then the Hopfield network can perform as robust content-addressable memory, resistant to connection alteration.
Simple Recurrent Networks
This special case of the basic architecture above was employed by Jeff Elman and Michael I. Jordan. A three-layer network is used, with the addition of a set of "context units" in the input layer. There are connections from the hidden layer (Elman) or from the output layer (Jordan) to these context units fixed with a weight of one[15]. At each time step, the input is propagated in a standard feed-forward fashion, and then a simple backprop-like learning rule is applied (this rule is not performing proper gradient descent, however). The fixed back connections result in the context units always maintaining a copy of the previous values of the hidden units (since they propagate over the connections before the learning rule is applied).
Echo state network
The echo state network (ESN) is a recurrent neural network with a sparsely connected random hidden layer. The weights of output neurons are the only part of the network that can change and be trained. ESN are good at reproducing certain time series [16]. A variant for spiking neurons is known as Liquid state machines[17].
Long short term memory network
The Long short term memory (LSTM) is an artificial neural net structure that unlike traditional RNNs doesn't have the problem of vanishing gradients. It works even when there are long delays, and it can handle signals that have a mix of low and high frequency components. LSTM RNN outperformed other RNN and other sequence learning methods methods such as HMM in numerous applications such as language learning[18] and connected handwriting recognition[19].
Bi-directional RNN
Invented by Schuster & Paliwal in 1997[20], bi-directional RNN or BRNN use a finite sequence to predict or label each element of the sequence based on both the past and the future context of the element. This is done by adding the outputs of two RNN, one processing the sequence from left to right, the other one from right to left. The combined outputs are the predictions of the teacher-given target signals. This technique proved to be especially useful when combined with LSTM RNN[21].
Hierarchical RNN
There are many instances of hierarchical RNN whose elements are connected in various ways to decompose hierarchical behavior into useful subprograms[22][23].
Stochastic neural networks
A stochastic neural network differs from a typical neural network because it introduces random variations into the network. In a probabilistic view of neural networks, such random variations can be viewed as a form of statistical sampling, such as Monte Carlo sampling.
Boltzmann machine
The Boltzmann machine can be thought of as a noisy Hopfield network. Invented by Geoff Hinton and Terry Sejnowski in 1985, the Boltzmann machine is important because it is one of the first neural networks to demonstrate learning of latent variables (hidden units). Boltzmann machine learning was at first slow to simulate, but the contrastive divergence algorithm of Geoff Hinton (circa 2000) allows models such as Boltzmann machines and products of experts to be trained much faster.
Modular neural networks
Biological studies have shown that the human brain functions not as a single massive network, but as a collection of small networks. This realization gave birth to the concept of modular neural networks, in which several small networks cooperate or compete to solve problems.
Committee of machines
A committee of machines (CoM) is a collection of different neural networks that together "vote" on a given example. This generally gives a much better result compared to other neural network models. Because neural networks suffer from local minima, starting with the same architecture and training but using different initial random weights often gives vastly different networks[citation needed]. A CoM tends to stabilize the result.
The CoM is similar to the general machine learning bagging method, except that the necessary variety of machines in the committee is obtained by training from different random starting weights rather than training on different randomly selected subsets of the training data.
Associative neural network (ASNN)
The ASNN is an extension of the committee of machines that goes beyond a simple/weighted average of different models. ASNN represents a combination of an ensemble of feed-forward neural networks and the k-nearest neighbor technique (kNN). It uses the correlation between ensemble responses as a measure of distance amid the analyzed cases for the kNN. This corrects the bias of the neural network ensemble. An associative neural network has a memory that can coincide with the training set. If new data become available, the network instantly improves its predictive ability and provides data approximation (self-learn the data) without a need to retrain the ensemble. Another important feature of ASNN is the possibility to interpret neural network results by analysis of correlations between data cases in the space of models. The method is demonstrated at www.vcclab.org, where you can either use it online or download it.
Physical neural network
A physical neural network includes electrically adjustable resistance material to simulate artificial synapses. Examples include the ADALINE neural network developed by Bernard Widrow in the 1960's and the memristor based neural network developed by Greg Snider of HP Labs in 2008.
Other types of networks
These special networks do not fit in any of the previous categories.
Holographic associative memory
Holographic associative memory represents a family of analog, correlation-based, associative, stimulus-response memories, where information is mapped onto the phase orientation of complex numbers operating.
Instantaneously trained networks
Instantaneously trained neural networks (ITNNs) were inspired by the phenomenon of short-term learning that seems to occur instantaneously. In these networks the weights of the hidden and the output layers are mapped directly from the training vector data. Ordinarily, they work on binary data, but versions for continuous data that require small additional processing are also available.
Spiking neural networks
Spiking neural networks (SNNs) are models which explicitly take into account the timing of inputs. The network input and output are usually represented as series of spikes (delta function or more complex shapes). SNNs have an advantage of being able to process information in the time domain (signals that vary over time). They are often implemented as recurrent networks. SNNs are also a form of pulse computer.
Spiking neural networks with axonal conduction delays exhibit polychronization, and hence could have a very large memory capacity.[24]
Networks of spiking neurons — and the temporal correlations of neural assemblies in such networks — have been used to model figure/ground separation and region linking in the visual system (see, for example, Reitboeck et al.in Haken and Stadler: Synergetics of the Brain. Berlin, 1989).
In June 2005 IBM announced construction of a Blue Gene supercomputer dedicated to the simulation of a large recurrent spiking neural network.[25]
Gerstner and Kistler have a freely available online textbook on Spiking Neuron Models.
Dynamic neural networks
Dynamic neural networks not only deal with nonlinear multivariate behaviour, but also include (learning of) time-dependent behaviour such as various transient phenomena and delay effects. Techniques to estimate a system process from observed data fall under the general category of system identification.
Cascading neural networks
Cascade-Correlation is an architecture and supervised learning algorithm developed by Scott Fahlman and Christian Lebiere. Instead of just adjusting the weights in a network of fixed topology, Cascade-Correlation begins with a minimal network, then automatically trains and adds new hidden units one by one, creating a multi-layer structure. Once a new hidden unit has been added to the network, its input-side weights are frozen. This unit then becomes a permanent feature-detector in the network, available for producing outputs or for creating other, more complex feature detectors. The Cascade-Correlation architecture has several advantages over existing algorithms: it learns very quickly, the network determines its own size and topology, it retains the structures it has built even if the training set changes, and it requires no back-propagation of error signals through the connections of the network. See: Cascade correlation algorithm.
Neuro-fuzzy networks
A neuro-fuzzy network is a fuzzy inference system in the body of an artificial neural network. Depending on the FIS type, there are several layers that simulate the processes involved in a fuzzy inference like fuzzification, inference, aggregation and defuzzification. Embedding an FIS in a general structure of an ANN has the benefit of using available ANN training methods to find the parameters of a fuzzy system.
Compositional pattern-producing networks
Compositional pattern-producing networks (CPPNs) are a variation of ANNs which differ in their set of activation functions and how they are applied. While typical ANNs often contain only sigmoid functions (and sometimes Gaussian functions), CPPNs can include both types of functions and many others. Furthermore, unlike typical ANNs, CPPNs are applied across the entire space of possible inputs so that they can represent a complete image. Since they are compositions of functions, CPPNs in effect encode images at infinite resolution and can be sampled for a particular display at whatever resolution is optimal.
One-shot associative memory
This type of network can add new patterns without the need for re-training. It is done by creating a specific memory structure, which assigns each new pattern to an orthogonal plane using adjacently connected hierarchical arrays [26]. The network offers real-time pattern recognition and high scalability, it however requires parallel processing and is thus best suited for platforms such as Wireless sensor networks (WSN), Grid computing, and GPGPUs.
Theoretical properties
Computational power
The multi-layer perceptron (MLP) is a universal function approximator, as proven by the Cybenko theorem. However, the proof is not constructive regarding the number of neurons required or the settings of the weights.
Work by Hava Siegelmann and Eduardo D. Sontag has provided a proof that a specific recurrent architecture with rational valued weights (as opposed to full precision real number-valued weights) has the full power of a Universal Turing Machine[27] using a finite number of neurons and standard linear connections. They have further shown that the use of irrational values for weights results in a machine with super-Turing power.
Capacity
Artificial neural network models have a property called 'capacity', which roughly corresponds to their ability to model any given function. It is related to the amount of information that can be stored in the network and to the notion of complexity.
Convergence
Nothing can be said in general about convergence since it depends on a number of factors. Firstly, there may exist many local minima. This depends on the cost function and the model. Secondly, the optimization method used might not be guaranteed to converge when far away from a local minimum. Thirdly, for a very large amount of data or parameters, some methods become impractical. In general, it has been found that theoretical guarantees regarding convergence are an unreliable guide to practical application.
Generalisation and statistics
In applications where the goal is to create a system that generalises well in unseen examples, the problem of overtraining has emerged. This arises in overcomplex or overspecified systems when the capacity of the network significantly exceeds the needed free parameters. There are two schools of thought for avoiding this problem: The first is to use cross-validation and similar techniques to check for the presence of overtraining and optimally select hyperparameters such as to minimize the generalisation error. The second is to use some form of regularisation. This is a concept that emerges naturally in a probabilistic (Bayesian) framework, where the regularisation can be performed by selecting a larger prior probability over simpler models; but also in statistical learning theory, where the goal is to minimize over two quantities: the 'empirical risk' and the 'structural risk', which roughly corresponds to the error over the training set and the predicted error in unseen data due to overfitting.

Supervised neural networks that use an MSE cost function can use formal statistical methods to determine the confidence of the trained model. The MSE on a validation set can be used as an estimate for variance. This value can then be used to calculate the confidence interval of the output of the network, assuming a normal distribution. A confidence analysis made this way is statistically valid as long as the output probability distribution stays the same and the network is not modified.
By assigning a softmax activation function on the output layer of the neural network (or a softmax component in a component-based neural network) for categorical target variables, the outputs can be interpreted as posterior probabilities. This is very useful in classification as it gives a certainty measure on classifications.
The softmax activation function is:
Dynamic properties
This article needs attention from an expert in Technology. Please add a reason or a talk parameter to this template to explain the issue with the article. (November 2008) |
Various techniques originally developed for studying disordered magnetic systems (i.e., the spin glass) have been successfully applied to simple neural network architectures, such as the Hopfield network. Influential work by E. Gardner and B. Derrida has revealed many interesting properties about perceptrons with real-valued synaptic weights, while later work by W. Krauth and M. Mezard has extended these principles to binary-valued synapses.
Gallery
-
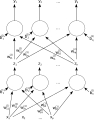
A single-layer feedforward artificial neural network. Arrows originating from are omitted for clarity. There are p inputs to this network and q outputs. There is no activation function (or equivalently, the activation function is ). In this system, the value of the qth output, would be calculated as
-
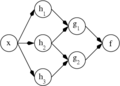
A two-layer feedforward artificialneural network.
See also
- 20Q
- Adaptive resonance theory
- Artificial life
- Associative memory
- Autoencoder
- Biological neural network
- Biologically inspired computing
- Blue brain
- Clinical decision support system
- Connectionist expert system
- Decision tree
- Expert system
- Fuzzy logic
- Genetic algorithm
- In Situ Adaptive Tabulation
- Linear discriminant analysis
- Logistic regression
- Memristor
- Multilayer perceptron
- Nearest neighbor (pattern recognition)
- Neural network
- Neuroevolution, NeuroEvolution of Augmented Topologies (NEAT)
- Neural network software
- Ni1000 chip
- Optical neural network
- Particle swarm optimization
- Perceptron
- Predictive analytics
- Principal components analysis
- Regression analysis
- Simulated annealing
- Systolic array
- Time delay neural network (TDNN)
References
- ^ "The Machine Learning Dictionary".
- ^ Roman M. Balabin, Ekaterina I. Lomakina (2009). "Neural network approach to quantum-chemistry data: Accurate prediction of density functional theory energies". J. Chem. Phys. 131 (7): 074104. doi:10.1063/1.3206326.
- ^ P. J. Werbos. Generalization of backpropagation with application to a recurrent gas market model. Neural Networks, 1, 1988.
- ^ David E. Rumelhart; Geoffrey E. Hinton; Ronald J. Williams. Learning Internal Representations by Error Propagation.
- ^ A. J. Robinson and F. Fallside. The utility driven dynamic error propagation network. Technical Report CUED/F-INFENG/TR.1, Cambridge University Engineering Department, 1987.
- ^ R. J. Williams and D. Zipser. Gradient-based learning algorithms for recurrent networks and their computational complexity. In Back-propagation: Theory, Architectures and Applications. Hillsdale, NJ: Erlbaum, 1994.
- ^ J. Schmidhuber. A local learning algorithm for dynamic feedforward and recurrent networks. Connection Science, 1(4):403–412, 1989.
- ^ Neural and Adaptive Systems: Fundamentals through Simulation. J.C. Principe, N.R. Euliano, W.C. Lefebvre
- ^ J. Schmidhuber. A fixed size storage O(n3) time complexity learning algorithm for fully recurrent continually running networks. Neural Computation, 4(2):243–248, 1992.
- ^ R. J. Williams. Complexity of exact gradient computation algorithms for recurrent neural networks. Technical Report Technical Report NU-CCS-89-27, Boston: Northeastern University, College of Computer Science, 1989.
- ^ B. A. Pearlmutter. Learning state space trajectories in recurrent neural networks. Neural Computation, 1(2):263–269, 1989.
- ^ S. Hochreiter. Untersuchungen zu dynamischen neuronalen Netzen. Diploma thesis, Institut f. Informatik, Technische Univ. Munich, 1991.
- ^ S. Hochreiter, Y. Bengio, P. Frasconi, and J. Schmidhuber. Gradient flow in recurrent nets: the difficulty of learning long-term dependencies. In S. C. Kremer and J. F. Kolen, editors, A Field Guide to Dynamical Recurrent Neural Networks. IEEE Press, 2001.
- ^ S. Hochreiter and J. Schmidhuber. Long short-term memory. Neural Computation, 9(8):1735– 1780, 1997.
- ^ Neural Networks as Cybernetic Systems 2nd and revised edition, Holk Cruse [1]
- ^ H. Jaeger. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science, 304:78–80, 2004.
- ^ W. Maass, T. Natschläger, and H. Markram. A fresh look at real-time computation in generic recurrent neural circuits. Technical report, Institute for Theoretical Computer Science, TU Graz, 2002.
- ^ F. A. Gers and J. Schmidhuber. LSTM recurrent networks learn simple context free and context sensitive languages. IEEE Transactions on Neural Networks, 12(6):1333–1340, 2001.
- ^ A. Graves, J. Schmidhuber. Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks. Advances in Neural Information Processing Systems 22, NIPS'22, p 545-552, Vancouver, MIT Press, 2009.
- ^ Mike Schuster and Kuldip K. Paliwal. Bidirectional recurrent neural networks. IEEE Trans- actions on Signal Processing, 45:2673–2681, November 1997.
- ^ A. Graves and J. Schmidhuber. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Networks, 18:602–610, 2005.
- ^ J. Schmidhuber. Learning complex, extended sequences using the principle of history compression. Neural Computation, 4(2):234-242, 1992
- ^ Dynamic Representation of Movement Primitives in an Evolved Recurrent Neural Network
- ^ Izhikevich EM (2006). "Polychronization: computation with spikes". Neural Comput. 18 (2): 245–82. doi:10.1162/089976606775093882. PMID 16378515.
{{cite journal}}: Unknown parameter|month=ignored (help) - ^ "IBM Research | Press Resources | IBM and EPFL Join Forces to Uncover the Secrets of Cognitive Intelligence". Retrieved 2009-05-02.
- ^ B.B. Nasution, A.I. Khan, A Hierarchical Graph Neuron Scheme for Real-Time Pattern Recognition, IEEE Transactions on Neural Networks, vol 19(2), 212-229, Feb. 2008
- ^ Siegelmann, H.T.; Sontag, E.D. (1991). "Turing computability with neural nets" (PDF). Appl. Math. Lett. 4 (6): 77–80.
Bibliography
- Bar-Yam, Yaneer (2003). Dynamics of Complex Systems, Chapter 2.
{{cite book}}: External link in|title= - Bar-Yam, Yaneer (2003). Dynamics of Complex Systems, Chapter 3.
{{cite book}}: External link in|title= - Bar-Yam, Yaneer (2005). Making Things Work.
{{cite book}}: External link in|title= - Bhadeshia H. K. D. H. (1999). "Neural Networks in Materials Science". ISIJ International. 39: 966–979. doi:10.2355/isijinternational.39.966.
{{cite journal}}: External link in|title= - Bhagat, P.M. (2005) Pattern Recognition in Industry, Elsevier. ISBN 0-08-044538-1
- Bishop, C.M. (1995) Neural Networks for Pattern Recognition, Oxford: Oxford University Press. ISBN 0-19-853849-9 (hardback) or ISBN 0-19-853864-2 (paperback)
- Cybenko, G.V. (1989). Approximation by Superpositions of a Sigmoidal function, Mathematics of Control, Signals and Systems, Vol. 2 pp. 303–314. electronic version
- Duda, R.O., Hart, P.E., Stork, D.G. (2001) Pattern classification (2nd edition), Wiley, ISBN 0-471-05669-3
- Egmont-Petersen, M., de Ridder, D., Handels, H. (2002). "Image processing with neural networks - a review". Pattern Recognition. 35 (10): 2279–2301. doi:10.1016/S0031-3203(01)00178-9+.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Gurney, K. (1997) An Introduction to Neural Networks London: Routledge. ISBN 1-85728-673-1 (hardback) or ISBN 1-85728-503-4 (paperback)
- Haykin, S. (1999) Neural Networks: A Comprehensive Foundation, Prentice Hall, ISBN 0-13-273350-1
- Fahlman, S, Lebiere, C (1991). The Cascade-Correlation Learning Architecture, created for National Science Foundation, Contract Number EET-8716324, and Defense Advanced Research Projects Agency (DOD), ARPA Order No. 4976 under Contract F33615-87-C-1499. electronic version
- Hertz, J., Palmer, R.G., Krogh. A.S. (1990) Introduction to the theory of neural computation, Perseus Books. ISBN 0-201-51560-1
- Lawrence, Jeanette (1994) Introduction to Neural Networks, California Scientific Software Press. ISBN 1-883157-00-5
- Masters, Timothy (1994) Signal and Image Processing with Neural Networks, John Wiley & Sons, Inc. ISBN 0-471-04963-8
- Ness, Erik. 2005. SPIDA-Web. Conservation in Practice 6(1):35-36. On the use of artificial neural networks in species taxonomy.
- Ripley, Brian D. (1996) Pattern Recognition and Neural Networks, Cambridge
- Siegelmann, H.T. and Sontag, E.D. (1994). Analog computation via neural networks, Theoretical Computer Science, v. 131, no. 2, pp. 331–360. electronic version
- Sergios Theodoridis, Konstantinos Koutroumbas (2009) "Pattern Recognition" , 4th Edition, Academic Press, ISBN: 978-1-59749-272-0.
- Smith, Murray (1993) Neural Networks for Statistical Modeling, Van Nostrand Reinhold, ISBN 0-442-01310-8
- Wasserman, Philip (1993) Advanced Methods in Neural Computing, Van Nostrand Reinhold, ISBN 0-442-00461-3
Further reading
External links
- Performance comparison of neural network algorithms tested on UCI data sets
- A close view to Artificial Neural Networks Algorithms
- Template:Dmoz
- A Brief Introduction to Neural Networks (D. Kriesel) - Illustrated, bilingual manuscript about artificial neural networks; Topics so far: Perceptrons, Backpropagation, Radial Basis Functions, Recurrent Neural Networks, Self Organizing Maps, Hopfield Networks.
- Neural Networks in Materials Science
- A practical tutorial on Neural Networks
- Applications of neural networks
- Articles to be merged from November 2008
- Articles to be split from August 2009
- Articles needing cleanup from May 2009
- Cleanup tagged articles without a reason field from May 2009
- Wikipedia pages needing cleanup from May 2009
- Machine learning
- Computational statistics
- Neural networks
- Classification algorithms
- Optimization algorithms
- Computational neuroscience























![{\displaystyle C=E\left[(f(x)-y)^{2}\right]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/36ef7e092e3f5c1ee571a4ebdefbedf4a90fc71b)








![{\displaystyle C=E[(x-f(x))^{2}]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/c1f91640816543aa11f268154dee167570010db7)