List of regular polytopes

Example regular polytopes

Regular (2D) polygons
Convex	Star
{5}	{5/2}
Regular (3D) polyhedra
Convex	Star
{5,3}	{5,5/2}
Regular 2D tessellations
Euclidean	Hyperbolic
{4,4}	{5,4}
Regular 4D polytopes
Convex	Star
{4,3,3}	{5/2,3,3}
Regular 3D tessellations
Euclidean	Hyperbolic
{4,3,4}	{5,3,4}

This page lists the regular polytopes in Euclidean, spherical and hyperbolic spaces. The Schläfli symbol notation describes every regular polytope, and is used widely below as a compact reference name for each.

The regular polytopes are grouped by dimension and subgrouped by convex, nonconvex and infinite forms. Nonconvex forms use the same vertices as the convex forms, but have intersecting facets. Infinite forms tessellate a one-lower-dimensional Euclidean space.

Infinite forms can be extended to tessellate a hyperbolic space. Hyperbolic space is like normal space at a small scale, but parallel lines diverge at a distance. This allows vertex figures to have negative angle defects, like making a vertex with 7 equilateral triangles and allowing it to lie flat. It cannot be done in a regular plane, but can be at the right scale of a hyperbolic plane.

Overview

This table shows a summary of regular polytope counts by dimension.

Dimension	Convex	Star	Convex Euclidean tessellations	Compact hyperbolic tessellations	Star hyperbolic tessellations	Paracompact hyperbolic tessellations	Abstract Polytopes
1	1 line segment	0	1	0	0	0	1
2	∞ polygons	∞ star polygons	1	1	0	0	∞
3	5 Platonic	4 Kepler–Poinsot	3 tilings	∞	∞	∞	∞
4	6 4-polytopes	10 Schläfli–Hess	1 3-honeycombs	4	0	11	∞
5	3 5-polytopes	0	3 4-honeycombs	5	4	2	∞
6	3 6-polytopes	0	1 5-honeycombs	0	0	5	∞
7+	3	0	1	0	0	0	∞

There are no nonconvex Euclidean regular tessellations in any number of dimensions.

Tessellations

The classical convex polytopes may be considered tessellations, or tilings, of spherical space. Tessellations of euclidean and hyperbolic space may also be considered regular polytopes. Note that an 'n'-dimensional polytope actually tessellates a space of one dimension less. For example, the (three-dimensional) platonic solids tessellate the 'two'-dimensional 'surface' of the sphere.

One dimension

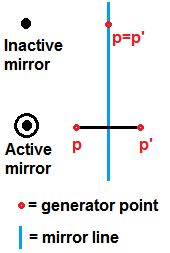
A Coxeter diagram represent mirror "planes" as nodes, and puts a ring around a node if a point is not on the plane. A ditel, { }, is a point p and its mirror image point p', and the line segment between them.

A one-dimensional polytope or 1-polytope is a closed line segment, bounded by its two endpoints. A 1-polytope is regular by definition and is represented by Schläfli symbol { }, or Coxeter diagram with a single ringed node, . Norman Johnson calls it a ditel.

Although trivial as a polytope, it appears as the edges of polygons and other higher dimensional polytopes. It is used in the definition of uniform prisms like Schläfli symbol { }×{p}, or Coxeter diagram as a Cartesian product of a line segment and a regular polygon.

Two dimensions (polygons)

The two-dimensional polytopes are called polygons. Regular polygons are equilateral and cyclic. A p-gonal regular polygon is represented by Schläfli symbol {p}.

Usually only convex polygons are considered regular, but star polygons, like the pentagram, can also be considered regular. They use the same vertices as the convex forms, but connect in an alternate connectivity which passes around the circle more than once to complete.

Star polygons should be called nonconvex rather than concave because the intersecting edges do not generate new vertices and all the vertices exist on a circle boundary.

Convex

The Schläfli symbol {p} represents a regular p-gon.

Name	Triangle (2-simplex)	Square (2-orthoplex) (2-cube)	Pentagon	Hexagon	Heptagon	Octagon
Schläfli	{3}	{4}	{5}	{6}	{7}	{8}
Symmetry	D3, [3]	D4, [4]	D5, [5]	D6, [6]	D7, [7]	D8, [8]
Coxeter
Image
Name	Enneagon	Decagon	Hendecagon	Dodecagon	Tridecagon	Tetradecagon
Schläfli	{9}	{10}	{11}	{12}	{13}	{14}
Symmetry	D9, [9]	D10, [10]	D11, [11]	D12, [12]	D13, [13]	D14, [14]
Dynkin
Image
Name	Pentadecagon	Hexadecagon	Heptadecagon	Octadecagon	Enneadecagon	Icosagon	...p-gon
Schläfli	{15}	{16}	{17}	{18}	{19}	{20}	{p}
Symmetry	D15, [15]	D16, [16]	D17, [17]	D18, [18]	D19, [19]	D20, [20]	Dp, [p]
Dynkin
Image

Improper (spherical)

The regular monogon {1} and regular digon {2} can be considered degenerate regular polygons. They can exist in non-Euclidean spaces like on the surface of a sphere or torus.

Name	Monogon	Digon
Schläfli symbol	{1} = h{2}	{2} = h{4}
Symmetry	D1, [1]	D2, [2]
Coxeter diagram
Image

Non-convex

There exist infinitely many non-convex regular polytopes in two dimensions, whose Schläfli symbols consist of rational numbers {n/m}. They are called star polygons and share the same vertex arrangements of the convex regular polygons.

In general, for any natural number n, there are n-pointed non-convex regular polygonal stars with Schläfli symbols {n/m} for all m such that m < n/2 (strictly speaking {n/m}={n/(n−m)}) and m and n are coprime.

Name	Pentagram	Heptagrams		Octagram	Enneagrams		Decagram	...n-agrams
Schläfli	{5/2}	{7/2}	{7/3}	{8/3}	{9/2}	{9/4}	{10/3}	{p/q}
Symmetry	D5, [5]	D7, [7]		D8, [8]	D9, [9],		D10, [10]	Dp, [p]
Coxeter
Image

Tessellations

There is one tessellation of the line, giving one polytope, the (two-dimensional) apeirogon (aze). This has infinitely many vertices and edges. Its Schläfli symbol is {∞}, and Coxeter diagram .

......

Three dimensions (polyhedra)

In three dimensions, polytopes are called polyhedra:

A regular polyhedron with Schläfli symbol {p,q}, Coxeter diagrams , has a regular face type {p}, and regular vertex figure {q}.

A vertex figure (of a polyhedron) is a polygon, seen by connecting those vertices which are one edge away from a given vertex. For regular polyhedra, this vertex figure is always a regular (and planar) polygon.

Existence of a regular polyhedron {p,q} is constrained by an inequality, related to the vertex figure's angle defect:

$1/p+1/q>1/2$ : Polyhedron (existing in Euclidean 3-space)

$1/p+1/q=1/2$ : Euclidean plane tiling

$1/p+1/q<1/2$ : Hyperbolic plane tiling

By enumerating the permutations, we find 5 convex forms, 4 star forms and 3 plane tilings, all with polygons {p} and {q} limited to: {3}, {4}, {5}, {5/2}, and {6}.

Beyond Euclidean space, there is an infinite set of regular hyperbolic tilings.

Convex

The convex regular polyhedra are called the 5 Platonic solids. The vertex figure is given with each vertex count. All these polyhedra have an Euler characteristic (χ) of 2.

Name	Schläfli {p,q}	Coxeter	Image (transparent)	Image (solid)	Image (sphere)	Faces {p}	Edges	Vertices {q}	Symmetry	Dual
Tetrahedron (3-simplex)	{3,3}					4 {3}	6	4 {3}	Td [3,3] (*332)	(self)
Hexahedron Cube (3-cube)	{4,3}					6 {4}	12	8 {3}	Oh [4,3] (*432)	Octahedron
Octahedron (3-orthoplex)	{3,4}					8 {3}	12	6 {4}	Oh [4,3] (*432)	Cube
Dodecahedron	{5,3}					12 {5}	30	20 {3}	Ih [5,3] (*532)	Icosahedron
Icosahedron	{3,5}					20 {3}	30	12 {5}	Ih [5,3] (*532)	Dodecahedron

Improper (spherical)

In spherical geometry, regular spherical polyhedra (tilings of the sphere) exist that would otherwise be degenerate as polytopes. These are the hosohedra {2,n}, their dual dihedra {n,2} and monohedron {1,1}. Coxeter calls these cases "improper" tessellations.

Some include:

Name	Schläfli {p,q}	Coxeter diagram	Image (sphere)	Faces {p}	Edges { }	Vertices {q}	Symmetry	Dual
Monohedron (half monogonal hosohedron)	{1,1} =h{2,1}			1 {1}	0 { }	1 {1}	C1v [ ] (*1)	Self
Monogonal hosohedron	{2,1}			1 {2}	1 { }	2 {1}	D1h [2,1] (*22)	Monogonal dihedron
Digonal hosohedron (Same as digonal dihedron)	{2,2}			2 {2}	2 { }	2 {2}	D2h [2,2] (*222)	Self
Trigonal hosohedron	{2,3}			3 {2}	3 { }	2 {3}	D3h [2,3] (*322)	Trigonal dihedron
Square hosohedron	{2,4}			4 {2}	4 { }	2 {4}	D4h [2,4] (*422)	Square dihedron
Pentagonal hosohedron	{2,5}			5 {2}	5 { }	2 {5}	D5h [2,5] (*522)	Pentagonal dihedron
Hexagonal hosohedron	{2,6}			6 {2}	6 { }	2 {6}	D6h [2,6] (*622)	Hexagonal dihedron
Monogonal dihedron (half monogonal hosohedron)	{1,2} =h{2,2}			2 {1}	1 { }	1 {2}	D1h [1,2] (*22)	Monogonal hosohedron
Digonal dihedron (Same as digonal hosohedron)	{2,2}			2 {2}	2 { }	2 {2}	D2h [2,2] (*222)	Self
Trigonal dihedron	{3,2}			2 {3}	3 { }	3 {2}	D3h [3,2] (*322)	Trigonal hosohedron
Square dihedron	{4,2}			2 {4}	4 { }	4 {2}	D4h [4,2] (*422)	Square hosohedron
Pentagonal dihedron	{5,2}			2 {5}	5 { }	5 {2}	D5h [5,2] (*522)	Pentagonal hosohedron
Hexagonal dihedron	{6,2}			2 {6}	6 { }	6 {2}	D6h [6,2] (*622)	Hexagonal hosohedron

Non-convex

The regular star polyhedra are called the Kepler–Poinsot polyhedra and there are four of them, based on the vertex arrangements of the dodecahedron {5,3} and icosahedron {3,5}:

As spherical tilings, these nonconvex forms overlap the sphere multiple times, called its density, being 3 or 7 for these forms. The tiling images show a single spherical polygon face in yellow.

Name	Image (transparent)	Image (solid)	Image (sphere)	Stellation diagram	Schläfli {p,q} and Coxeter	Faces {p}	Edges	Vertices {q} verf.	χ	Density	Symmetry	Dual
Small stellated dodecahedron					{5/2,5}	12 {5/2}	30	12 {5}	−6	3	Ih [5,3] (*532)	Great dodecahedron
Great dodecahedron					{5,5/2}	12 {5}	30	12 {5/2}	−6	3	Ih [5,3] (*532)	Small stellated dodecahedron
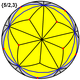
Great stellated dodecahedron					{5/2,3}	12 {5/2}	30	20 {3}	2	7	Ih [5,3] (*532)	Great icosahedron
Great icosahedron					{3,5/2}	20 {3}	30	12 {5/2}	2	7	Ih [5,3] (*532)	Great stellated dodecahedron

Tessellations

Euclidean tilings

There are three regular tessellations of the plane. All three have an Euler characteristic (χ) of 0.

Name	Square tiling (quadrille)	Triangular tiling (deltille)	Hexagonal tiling (hextille)
Symmetry	p4m, [4,4]	p6m, [6,3]
Schläfli {p,q}	{4,4}	{3,6}	{6,3}
Coxeter diagram
Image
Symmetry	*442 (p4m)	*632 (p6m)

There is one degenerate regular tiling, {∞,2} (azat), made from two apeirogons, each filling half the plane. This tiling is related to a 2-faced dihedron, {p,2}, on the sphere.

Euclidean star-tilings

There are no regular plane tilings of star polygons. There are many enumerations that fit in the plane (1/p + 1/q = 1/2), like {8/3,8}, {10/3,5}, {5/2,10}, {12/5,12}, etc., but none repeat periodically.

Hyperbolic tilings

Tessellations of hyperbolic 2-space can be called hyperbolic tilings. There are infinitely many regular tilings in H². As stated above, every positive integer pair {p,q} such that 1/p + 1/q < 1/2 gives a hyperbolic tiling. In fact, for the general Schwarz triangle (p, q, r) the same holds true for 1/p + 1/q + 1/r < 1.

There are a number of different ways to display the hyperbolic plane, including the Poincaré disc model which maps the plane into a circle, as shown below. It should be recognized that all of the polygon faces in the tilings below are equal-sized and only appear to get smaller near the edges due to the projection applied, very similar to the effect of a camera fisheye lens.

A sampling:

Regular hyperbolic tiling table
Spherical (improper/Platonic)/Euclidean/hyperbolic (Poincaré disc: compact/paracompact/noncompact) tessellations with their Schläfli symbol
p \ q	2	3	4	5	6	7	8	...	∞	...	iπ/λ
2	{2,2}	{2,3}	{2,4}	{2,5}	{2,6}	{2,7}	{2,8}		{2,∞}		{2,iπ/λ}
3	{3,2}	(tetrahedron) {3,3}	(octahedron) {3,4}	(icosahedron) {3,5}	(deltille) {3,6}	{3,7}	{3,8}		{3,∞}		{3,iπ/λ}
4	{4,2}	(cube) {4,3}	(quadrille) {4,4}	{4,5}	{4,6}	{4,7}	{4,8}		{4,∞}		{4,iπ/λ}
5	{5,2}	(dodecahedron) {5,3}	{5,4}	{5,5}	{5,6}	{5,7}	{5,8}		{5,∞}		{5,iπ/λ}
6	{6,2}	(hextille) {6,3}	{6,4}	{6,5}	{6,6}	{6,7}	{6,8}		{6,∞}		{6,iπ/λ}
7	{7,2}	{7,3}	{7,4}	{7,5}	{7,6}	{7,7}	{7,8}		{7,∞}		{7,iπ/λ}
8	{8,2}	{8,3}	{8,4}	{8,5}	{8,6}	{8,7}	{8,8}		{8,∞}		{8,iπ/λ}
...
∞	{∞,2}	{∞,3}	{∞,4}	{∞,5}	{∞,6}	{∞,7}	{∞,8}	{∞,∞}	{∞,iπ/λ}
...
iπ/λ	{iπ/λ,2}	{iπ/λ,3}	{iπ/λ,4}	{iπ/λ,5}	{iπ/λ,6}	{iπ/λ,7}	{iπ/λ,8}	{iπ/λ,∞}	{iπ/λ, iπ/λ}

Hyperbolic star-tilings

There are 2 infinite forms of hyperbolic tilings whose faces or vertex figures are star polygons: {m/2, m} and their duals {m, m/2} with m = 7, 9, 11, .... The {m/2, m} tilings are stellations of the {m, 3} tilings while the {m, m/2} dual tilings are facetings of the {3, m} tilings and greatenings of the {m, 3} tilings.

The patterns {m/2, m} and {m, m/2} continue for odd m < 7 as polyhedra: when m = 5, we obtain the small stellated dodecahedron and great dodecahedron, and when m = 3, we obtain the tetrahedron. If m is even, depending on how we choose to define {m/2}, we can either obtain degenerate double covers of other tilings or compound tilings.

Name	Schläfli	Coxeter diagram	Image	Face type {p}	Vertex figure {q}	Density	Symmetry	Dual
Order-7 heptagrammic tiling	{7/2,7}			{7/2}	{7}	3	*732 [7,3]	Heptagrammic-order heptagonal tiling
Heptagrammic-order heptagonal tiling	{7,7/2}			{7}	{7/2}	3	*732 [7,3]	Order-7 heptagrammic tiling
Order-9 enneagrammic tiling	{9/2,9}			{9/2}	{9}	3	*932 [9,3]	Enneagrammic-order enneagonal tiling
Enneagrammic-order enneagonal tiling	{9,9/2}			{9}	{9/2}	3	*932 [9,3]	Order-9 enneagrammic tiling
Order-p p-grammic tiling	{p/2,p}			{p/2}	{p}	3	*p32 [p,3]	p-grammic-order p-gonal tiling
p-grammic-order p-gonal tiling	{p,p/2}			{p}	{p/2}	3	*p32 [p,3]	Order-p p-grammic tiling

Four dimensions

Regular 4-polytopes with Schläfli symbol $\{p,q,r\}$ have cells of type $\{p,q\}$, faces of type $\{p\}$, edge figures $\{r\}$, and vertex figures $\{q,r\}$.

• A vertex figure (of a 4-polytope) is a polyhedron, seen by the arrangement of neighboring vertices around a given vertex. For regular polychora, this vertex figure is a regular polyhedron.
• An edge figure is a polygon, seen by the arrangement of faces around an edge. For regular polychora, this edge figure will always be a regular polygon.

The existence of a regular 4-polytope $\{p,q,r\}$ is constrained by the existence of the regular polyhedra $\{p,q\},\{q,r\}$.

Each will exist in a space dependent upon this expression:

$\sin \left({\frac {\pi }{p}}\right)\sin \left({\frac {\pi }{r}}\right)-\cos \left({\frac {\pi }{q}}\right)$

$>0$ : Hyperspherical 3-space honeycomb or 4-polytope

$=0$ : Euclidean 3-space honeycomb

$<0$ : Hyperbolic 3-space honeycomb

These constraints allow for 21 forms: 6 are convex, 10 are nonconvex, one is a Euclidean 3-space honeycomb, and 4 are hyperbolic honeycombs.

The Euler characteristic $\chi$ for polychora is $\chi =V+F-E-C$ and is zero for all forms.

Convex

The 6 convex regular 4-polytopes are shown in the table below. All these polychora have an Euler characteristic (χ) of 0.

Name	Schläfli {p,q,r}	Coxeter	Cells {p,q}	Faces {p}	Edges {r}	Vertices {q,r}	Dual {r,q,p}
5-cell (4-simplex) (Pentachoron) (pen)	{3,3,3}		5 {3,3}	10 {3}	10 {3}	5 {3,3}	(self)
8-cell (4-cube) (Tesseract) (tes)	{4,3,3}		8 {4,3}	24 {4}	32 {3}	16 {3,3}	16-cell
16-cell (4-orthoplex) (hex)	{3,3,4}		16 {3,3}	32 {3}	24 {4}	8 {3,4}	Tesseract
24-cell (ico)	{3,4,3}		24 {3,4}	96 {3}	96 {3}	24 {4,3}	(self)
120-cell (hi)	{5,3,3}		120 {5,3}	720 {5}	1200 {3}	600 {3,3}	600-cell
600-cell (ex)	{3,3,5}		600 {3,3}	1200 {3}	720 {5}	120 {3,5}	120-cell

5-cell	8-cell	16-cell	24-cell	120-cell	600-cell
{3,3,3}	{4,3,3}	{3,3,4}	{3,4,3}	{5,3,3}	{3,3,5}
Wireframe (Petrie polygon) skew orthographic projections
Solid orthographic projections
tetrahedral envelope (cell/vertex-centered)	cubic envelope (cell-centered)	Cubic envelope (cell-centered)	cuboctahedral envelope (cell-centered)	truncated rhombic triacontahedron envelope (cell-centered)	Pentakis icosidodecahedral envelope (vertex-centered)
Wireframe Schlegel diagrams (Perspective projection)
(Cell-centered)	(Cell-centered)	(Cell-centered)	(Cell-centered)	(Cell-centered)	(Vertex-centered)
Wireframe stereographic projections (Hyperspherical)

Improper (spherical)

Dichora and hosochora exist as regular tessellations of the 3-sphere.

Regular dichora (2 facets) include: {3,3,2}, {3,4,2}, {4,3,2}, {5,3,2}, {3,5,2}, {p,2,2}, and their hosochora duals (2 vertices): {2,3,3}, {2,4,3}, {2,3,4}, {2,3,5}, {2,5,3}, {2,2,p}. Polychora of the form {2,p,2} are both dichora and hosochora.

Non-convex

There are ten regular star 4-polytopes, which are called the Schläfli–Hess 4-polytopes. Their vertices are based on the convex 120-cell {5,3,3} and 600-cell {3,3,5}.

Ludwig Schläfli found four of them and skipped the last six because he would not allow forms that failed the Euler characteristic on cells or vertex figures (for zero-hole tori: F+V−E=2). Edmund Hess (1843–1903) completed the full list of ten in his German book Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder (1883)[1].

There are 4 unique edge arrangements and 7 unique face arrangements from these 10 nonconvex polychora, shown as orthogonal projections:

Name	Wireframe	Solid	Schläfli {p, q, r} Coxeter	Cells {p, q}	Faces {p}	Edges {r}	Vertices {q, r}	Density	χ	Symmetry group	Dual {r, q,p}
Icosahedral 120-cell (faceted 600-cell) (fix)			{3,5,5/2}	120 {3,5}	1200 {3}	720 {5/2}	120 {5,5/2}	4	480	H4 [5,3,3]	Small stellated 120-cell
Small stellated 120-cell (sishi)			{5/2,5,3}	120 {5/2,5}	720 {5/2}	1200 {3}	120 {5,3}	4	−480	H4 [5,3,3]	Icosahedral 120-cell
Great 120-cell (gohi)			{5,5/2,5}	120 {5,5/2}	720 {5}	720 {5}	120 {5/2,5}	6	0	H4 [5,3,3]	Self-dual
Grand 120-cell (gahi)			{5,3,5/2}	120 {5,3}	720 {5}	720 {5/2}	120 {3,5/2}	20	0	H4 [5,3,3]	Great stellated 120-cell
Great stellated 120-cell (gishi)			{5/2,3,5}	120 {5/2,3}	720 {5/2}	720 {5}	120 {3,5}	20	0	H4 [5,3,3]	Grand 120-cell
Grand stellated 120-cell (gashi)			{5/2,5,5/2}	120 {5/2,5}	720 {5/2}	720 {5/2}	120 {5,5/2}	66	0	H4 [5,3,3]	Self-dual
Great grand 120-cell (gaghi)			{5,5/2,3}	120 {5,5/2}	720 {5}	1200 {3}	120 {5/2,3}	76	−480	H4 [5,3,3]	Great icosahedral 120-cell
Great icosahedral 120-cell (great faceted 600-cell) (gofix)			{3,5/2,5}	120 {3,5/2}	1200 {3}	720 {5}	120 {5/2,5}	76	480	H4 [5,3,3]	Great grand 120-cell
Grand 600-cell (gax)			{3,3,5/2}	600 {3,3}	1200 {3}	720 {5/2}	120 {3,5/2}	191	0	H4 [5,3,3]	Great grand stellated 120-cell
Great grand stellated 120-cell (gogishi)			{5/2,3,3}	120 {5/2,3}	720 {5/2}	1200 {3}	600 {3,3}	191	0	H4 [5,3,3]	Grand 600-cell

There are 4 failed potential nonconvex regular polychora permutations: {3,5/2,3}, {4,3,5/2}, {5/2,3,4}, {5/2,3,5/2}. Their cells and vertex figures exist, but they do not cover a hypersphere with a finite number of repetitions.

Tessellations of Euclidean 3-space

Edge framework of cubic honeycomb, {4,3,4}

There is only one non-degenerate regular tessellation of 3-space (honeycombs):

Name	Schläfli {p,q,r}	Coxeter	Cell type {p,q}	Face type {p}	Edge figure {r}	Vertex figure {q,r}	χ	Dual
Cubic honeycomb (chon)	{4,3,4}		{4,3}	{4}	{4}	{3,4}	0	Self-dual

Improper tessellations of Euclidean 3-space

Regular {2,4,4} honeycomb, seen projected into a sphere.

There are six improper regular tessellations, pairs based on the three regular Euclidean tilings. Their cells and vertex figures are all regular hosohedra {2,n}, dihedra, {n,2}, and Euclidean tilings. These improper regular tilings are constructionally related to prismatic uniform honeycombs by truncation operations. They are higher-dimensional analogues of the order-2 apeirogonal tiling and apeirogonal hosohedron.

Schläfli {p,q,r}	Coxeter diagram	Cell type {p,q}	Face type {p}	Edge figure {r}	Vertex figure {q,r}
{2,4,4}		{2,4}	{2}	{4}	{4,4}
{2,3,6}		{2,3}	{2}	{6}	{3,6}
{2,6,3}		{2,6}	{2}	{3}	{6,3}
{4,4,2}		{4,4}	{4}	{2}	{4,2}
{3,6,2}		{3,6}	{3}	{2}	{6,2}
{6,3,2}		{6,3}	{6}	{2}	{3,2}

Tessellations of hyperbolic 3-space

4 compact regular honeycombs {5,3,4} {5,3,5} {4,3,5} {3,5,3}

4 of 11 paracompact regular honeycombs {3,4,4} {3,6,3} {4,4,3} {4,4,4}

Tessellations of hyperbolic 3-space can be called hyperbolic honeycombs. There are 15 hyperbolic honeycombs in H³, 4 compact and 11 paracompact.

Name	Schläfli Symbol {p,q,r}	Coxeter	Cell type {p,q}	Face type {p}	Edge figure {r}	Vertex figure {q,r}	χ	Dual
Icosahedral honeycomb	{3,5,3}		{3,5}	{3}	{3}	{5,3}	0	Self-dual
Order-5 cubic honeycomb	{4,3,5}		{4,3}	{4}	{5}	{3,5}	0	{5,3,4}
Order-4 dodecahedral honeycomb	{5,3,4}		{5,3}	{5}	{4}	{3,4}	0	{4,3,5}
Order-5 dodecahedral honeycomb	{5,3,5}		{5,3}	{5}	{5}	{3,5}	0	Self-dual

There are also 11 paracompact H³ honeycombs (those with infinite (Euclidean) cells and/or vertex figures): {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5}, and {6,3,6}.

Name	Schläfli Symbol {p,q,r}	Coxeter	Cell type {p,q}	Face type {p}	Edge figure {r}	Vertex figure {q,r}	χ	Dual
Order-6 tetrahedral honeycomb	{3,3,6}		{3,3}	{3}	{6}	{3,6}	0	{6,3,3}
Hexagonal tiling honeycomb	{6,3,3}		{6,3}	{6}	{3}	{3,3}	0	{3,3,6}
Order-4 octahedral honeycomb	{3,4,4}		{3,4}	{3}	{4}	{4,4}	0	{4,4,3}
Square tiling honeycomb	{4,4,3}		{4,4}	{4}	{3}	{4,3}	0	{3,3,4}
Triangular tiling honeycomb	{3,6,3}		{3,6}	{3}	{3}	{6,3}	0	Self-dual
Order-6 cubic honeycomb	{4,3,6}		{4,3}	{4}	{4}	{3,4}	0	{6,3,4}
Order-4 hexagonal tiling honeycomb	{6,3,4}		{6,3}	{6}	{4}	{3,4}	0	{4,3,6}
Order-4 square tiling honeycomb	{4,4,4}		{4,4}	{4}	{4}	{4,4}	0	{4,4,4}
Order-6 dodecahedral honeycomb	{5,3,6}		{5,3}	{5}	{5}	{3,5}	0	{6,3,5}
Order-5 hexagonal tiling honeycomb	{6,3,5}		{6,3}	{6}	{5}	{3,5}	0	{5,3,6}
Order-6 hexagonal tiling honeycomb	{6,3,6}		{6,3}	{6}	{6}	{3,6}	0	Self-dual

A subset of uniform polychora and honeycombs are contained in the form {p,3,q} for values 3 to 6. Noncompact solutions exist as Lorentzian Coxeter groups for p or q greater than 6, and can be visualized with open domains in hyperbolic space, and a few are drawn below as tilings on the ideal half-space plane.

Spherical (improper/Platonic)/Euclidean/hyperbolic(compact/paracompact/noncompact) honeycombs {p,3,r}

{p,3} \ r	2	3	4	5	6	7	8	... ∞
{2,3}	{2,3,2}	{2,3,3}	{2,3,4}	{2,3,5}	{2,3,6}	{2,3,7}	{2,3,8}	{2,3,∞}
{3,3}	{3,3,2}	{3,3,3}	{3,3,4}	{3,3,5}	{3,3,6}	{3,3,7}	{3,3,8}	{3,3,∞}
{4,3}	{4,3,2}	{4,3,3}	{4,3,4}	{4,3,5}	{4,3,6}	{4,3,7}	{4,3,8}	{4,3,∞}
{5,3}	{5,3,2}	{5,3,3}	{5,3,4}	{5,3,5}	{5,3,6}	{5,3,7}	{5,3,8}	{5,3,∞}
{6,3}	{6,3,2}	{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{6,3,7}	{6,3,8}	{6,3,∞}
{7,3}	{7,3,2}	{7,3,3}	{7,3,4}	{7,3,5}	{7,3,6}	{7,3,7}	{7,3,8}	{7,3,∞}
{8,3}	{8,3,2}	{8,3,3}	{8,3,4}	{8,3,5}	{8,3,6}	{8,3,7}	{8,3,8}	{8,3,∞}
... {∞,3}	{∞,3,2}	{∞,3,3}	{∞,3,4}	{∞,3,5}	{∞,3,6}	{∞,3,7}	{∞,3,8}	{∞,3,∞}

{p,4,r} {p,4} \ r 2 3 4 5 6 ∞ {2,4} {2,4,2} {2,4,3} {2,4,4} {2,4,5} {2,4,6} {2,4,∞} {3,4} {3,4,2} {3,4,3} {3,4,4} {3,4,5} {3,4,6} {3,4,∞} {4,4} {4,4,2} {4,4,3} {4,4,4} {4,4,5} {4,4,6} {4,4,∞} {5,4} {5,4,2} {5,4,3} {5,4,4} {5,4,5} {5,4,6} {5,4,∞} {6,4} {6,4,2} {6,4,3} {6,4,4} {6,4,5} {6,4,6} {6,4,∞} {∞,4} {∞,4,2} {∞,4,3} {∞,4,4} {∞,4,5} {∞,4,6} {∞,4,∞}

{p,5,r} {p,5} \ r 2 3 4 5 6 ∞ {2,5} {2,5,2} {2,5,3} {2,5,4} {2,5,5} {2,5,6} {2,5,∞} {3,5} {3,5,2} {3,5,3} {3,5,4} {3,5,5} {3,5,6} {3,5,∞} {4,5} {4,5,2} {4,5,3} {4,5,4} {4,5,5} {4,5,6} {4,5,∞} {5,5} {5,5,2} {5,5,3} {5,5,4} {5,5,5} {5,5,6} {5,5,∞} {6,5} {6,5,2} {6,5,3} {6,5,4} {6,5,5} {6,5,6} {6,5,∞} {∞,5} {∞,5,2} {∞,5,3} {∞,5,4} {∞,5,5} {∞,5,6} {∞,5,∞}

{p,6,r} {p,6} \ r 2 3 4 5 6 ∞ {2,6} {2,6,2} {2,6,3} {2,6,4} {2,6,5} {2,6,6} {2,6,∞} {3,6} {3,6,2} {3,6,3} {3,6,4} {3,6,5} {3,6,6} {3,6,∞} {4,6} {4,6,2} {4,6,3} {4,6,4} {4,6,5} {4,6,6} {4,6,∞} {5,6} {5,6,2} {5,6,3} {5,6,4} {5,6,5} {5,6,6} {5,6,∞} {6,6} {6,6,2} {6,6,3} {6,6,4} {6,6,5} {6,6,6} {6,6,∞} {∞,6} {∞,6,2} {∞,6,3} {∞,6,4} {∞,6,5} {∞,6,6} {∞,6,∞}

{p,7,r} {p,7} \ r 2 3 4 5 6 ∞ {2,7} {2,7,2} {2,7,3} {2,7,4} {2,7,5} {2,7,6} {2,7,∞} {3,7} {3,7,2} {3,7,3} {3,7,4} {3,7,5} {3,7,6} {3,7,∞} {4,7} {4,7,2} {4,7,3} {4,7,4} {4,7,5} {4,7,6} {4,7,∞} {5,7} {5,7,2} {5,7,3} {5,7,4} {5,7,5} {5,7,6} {5,7,∞} {6,7} {6,7,2} {6,7,3} {6,7,4} {6,7,5} {6,7,6} {6,7,∞} {∞,7} {∞,7,2} {∞,7,3} {∞,7,4} {∞,7,5} {∞,7,6} {∞,7,∞}

{p,8,r} {p,8} \ r 2 3 4 5 6 ∞ {2,8} {2,8,2} {2,8,3} {2,8,4} {2,8,5} {2,8,6} {2,8,∞} {3,8} {3,8,2} {3,8,3} {3,8,4} {3,8,5} {3,8,6} {3,8,∞} {4,8} {4,8,2} {4,8,3} {4,8,4} {4,8,5} {4,8,6} {4,8,∞} {5,8} {5,8,2} {5,8,3} {5,8,4} {5,8,5} {5,8,6} {5,8,∞} {6,8} {6,8,2} {6,8,3} {6,8,4} {6,8,5} {6,8,6} {6,8,∞} {∞,8} {∞,8,2} {∞,8,3} {∞,8,4} {∞,8,5} {∞,8,6} {∞,8,∞}

{p,∞,r} {p,∞} \ r 2 3 4 5 6 ∞ {2,∞} {2,∞,2} {2,∞,3} {2,∞,4} {2,∞,5} {2,∞,6} {2,∞,∞} {3,∞} {3,∞,2} {3,∞,3} {3,∞,4} {3,∞,5} {3,∞,6} {3,∞,∞} {4,∞} {4,∞,2} {4,∞,3} {4,∞,4} {4,∞,5} {4,∞,6} {4,∞,∞} {5,∞} {5,∞,2} {5,∞,3} {5,∞,4} {5,∞,5} {5,∞,6} {5,∞,∞} {6,∞} {6,∞,2} {6,∞,3} {6,∞,4} {6,∞,5} {6,∞,6} {6,∞,∞} {∞,∞} {∞,∞,2} {∞,∞,3} {∞,∞,4} {∞,∞,5} {∞,∞,6} {∞,∞,∞}

Five and more dimensions

In five dimensions, a regular polytope can be named as $\{p,q,r,s\}$ where $\{p,q,r\}$ is the hypercell (or teron) type, $\{p,q\}$ is the cell type, $\{p\}$ is the face type, and $\{s\}$ is the face figure, $\{r,s\}$ is the edge figure, and $\{q,r,s\}$ is the vertex figure.

A 5-polytope has been called a polyteron, and if infinite (i.e. a honeycomb) a tetracomb.

A vertex figure (of a 5-polytope) is a 4-polytope, seen by the arrangement of neighboring vertices to each vertex.

An edge figure (of a 5-polytope) is a polyhedron, seen by the arrangement of faces around each edge.

A face figure (of a 5-polytope) is a polygon, seen by the arrangement of cells around each face.

A regular 5-polytope $\{p,q,r,s\}$ exists only if $\{p,q,r\}$ and $\{q,r,s\}$ are regular polychora.

The space it fits in is based on the expression:

${\frac {\cos ^{2}\left({\frac {\pi }{q}}\right)}{\sin ^{2}\left({\frac {\pi }{p}}\right)}}+{\frac {\cos ^{2}\left({\frac {\pi }{r}}\right)}{\sin ^{2}\left({\frac {\pi }{s}}\right)}}$

$<1$ : Spherical 4-space tessellation or 5-space polytope

$=1$ : Euclidean 4-space tessellation

$>1$ : hyperbolic 4-space tessellation

Enumeration of these constraints produce 3 convex polytopes, zero nonconvex polytopes, 3 4-space tessellations, and 5 hyperbolic 4-space tessellations. There are no non-convex regular polytopes in five dimensions or higher.

Higher-dimensional polytopes have sometimes received names. 6-polytopes have sometimes been called polypeta, 7-polytopes polyexa, 8-polytopes polyzetta, and 9-polytopes polyyotta.

Convex

In dimensions 5 and higher, there are only three kinds of convex regular polytopes.

Name	Schläfli Symbol {p1,...,pn−1}	Coxeter	k-faces	Facet type	Vertex figure	Dual
n-simplex	{3n−1}	...	${{n+1} \choose {k+1}}$	{3n−2}	{3n−2}	Self-dual
n-cube	{4,3n−2}	...	$2^{n-k}{n \choose k}$	{4,3n−3}	{3n−2}	n-orthoplex
n-orthoplex	{3n−2,4}	...	$2^{k+1}{n \choose {k+1}}$	{3n−2}	{3n−3,4}	n-cube

5 dimensions

Name	Schläfli Symbol {p,q,r,s} Coxeter	Facets {p,q,r}	Cells {p,q}	Faces {p}	Edges	Vertices	Face figure {s}	Edge figure {r,s}	Vertex figure {q,r,s}
5-simplex (hix)	{3,3,3,3}	6 {3,3,3}	15 {3,3}	20 {3}	15	6	{3}	{3,3}	{3,3,3}
5-cube (pent)	{4,3,3,3}	10 {4,3,3}	40 {4,3}	80 {4}	80	32	{3}	{3,3}	{3,3,3}
5-orthoplex (tac)	{3,3,3,4}	32 {3,3,3}	80 {3,3}	80 {3}	40	10	{4}	{3,4}	{3,3,4}

5-simplex

5-cube

5-orthoplex

6 dimensions

Name	Schläfli	Vertices	Edges	Faces	Cells	4-faces	5-faces	χ
6-simplex (hop)	{3,3,3,3,3}	7	21	35	35	21	7	0
6-cube (ax)	{4,3,3,3,3}	64	192	240	160	60	12	0
6-orthoplex (gee)	{3,3,3,3,4}	12	60	160	240	192	64	0

6-simplex

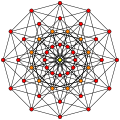6-cube

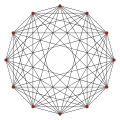6-orthoplex

7 dimensions

Name	Schläfli	Vertices	Edges	Faces	Cells	4-faces	5-faces	6-faces	χ
7-simplex (oca)	{3,3,3,3,3,3}	8	28	56	70	56	28	8	2
7-cube (hept)	{4,3,3,3,3,3}	128	448	672	560	280	84	14	2
7-orthoplex (zee)	{3,3,3,3,3,4}	14	84	280	560	672	448	128	2

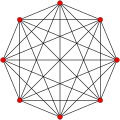7-simplex

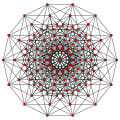7-cube

7-orthoplex

8 dimensions

Name	Schläfli	Vertices	Edges	Faces	Cells	4-faces	5-faces	6-faces	7-faces	χ
8-simplex (ene)	{3,3,3,3,3,3,3}	9	36	84	126	126	84	36	9	0
8-cube (octo)	{4,3,3,3,3,3,3}	256	1024	1792	1792	1120	448	112	16	0
8-orthoplex (ek)	{3,3,3,3,3,3,4}	16	112	448	1120	1792	1792	1024	256	0

8-simplex

8-cube

8-orthoplex

9 dimensions

Name	Schläfli	Vertices	Edges	Faces	Cells	4-faces	5-faces	6-faces	7-faces	8-faces	χ
9-simplex (day)	{38}	10	45	120	210	252	210	120	45	10	2
9-cube (enne)	{4,37}	512	2304	4608	5376	4032	2016	672	144	18	2
9-orthoplex (vee)	{37,4}	18	144	672	2016	4032	5376	4608	2304	512	2

9-simplex

9-cube

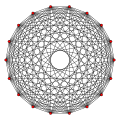9-orthoplex

10 dimensions

Name	Schläfli	Vertices	Edges	Faces	Cells	4-faces	5-faces	6-faces	7-faces	8-faces	9-faces	χ
10-simplex (ux)	{39}	11	55	165	330	462	462	330	165	55	11	0
10-cube (deker)	{4,38}	1024	5120	11520	15360	13440	8064	3360	960	180	20	0
10-orthoplex (ka)	{38,4}	20	180	960	3360	8064	13440	15360	11520	5120	1024	0

10-simplex

10-cube

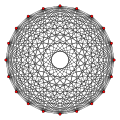10-orthoplex

...

Non-convex

There are no non-convex regular polytopes in five dimensions or higher.

Tessellations of Euclidean space

Tessellations of Euclidean 4-space

There are three kinds of infinite regular tessellations (honeycombs) that can tessellate Euclidean four-dimensional space:

Name	Schläfli Symbol {p,q,r,s}	Facet type {p,q,r}	Cell type {p,q}	Face type {p}	Face figure {s}	Edge figure {r,s}	Vertex figure {q,r,s}	Dual
Tesseractic honeycomb (test)	{4,3,3,4}	{4,3,3}	{4,3}	{4}	{4}	{3,4}	{3,3,4}	Self-dual
16-cell honeycomb (hext)	{3,3,4,3}	{3,3,4}	{3,3}	{3}	{3}	{4,3}	{3,4,3}	{3,4,3,3}
24-cell honeycomb (icot)	{3,4,3,3}	{3,4,3}	{3,4}	{3}	{3}	{3,3}	{4,3,3}	{3,3,4,3}

Projected portion of {4,3,3,4} (Tesseractic honeycomb)

Projected portion of {3,3,4,3} (16-cell honeycomb)

Projected portion of {3,4,3,3} (24-cell honeycomb)

Tessellations of Euclidean 5-space and higher

The hypercubic honeycomb is the only family of regular honeycomb that can tessellate each dimension, five or higher, formed by hypercube facets, four around every ridge.

Name	Schläfli {p1, p2, ..., pn−1}	Facet type	Vertex figure	Dual
Square tiling (squat)	{4,4}	{4}	{4}	Self-dual
Cubic honeycomb (chon)	{4,3,4}	{4,3}	{3,4}	Self-dual
Tesseractic honeycomb (test)	{4,32,4}	{4,32}	{32,4}	Self-dual
5-cube honeycomb (penth)	{4,33,4}	{4,33}	{33,4}	Self-dual
6-cube honeycomb	{4,34,4}	{4,34}	{34,4}	Self-dual
7-cube honeycomb	{4,35,4}	{4,35}	{35,4}	Self-dual
8-cube honeycomb	{4,36,4}	{4,36}	{36,4}	Self-dual
n-hypercubic honeycomb	{4,3n−2,4}	{4,3n−2}	{3n−2,4}	Self-dual

Tessellations of hyperbolic space

Tessellations of hyperbolic 4-space

There are seven convex regular honeycombs and four star-honeycombs in H⁴ space. Five convex ones are compact, and two are paracompact.

Five compact regular honeycombs in H⁴:

Name	Schläfli Symbol {p,q,r,s}	Facet type {p,q,r}	Cell type {p,q}	Face type {p}	Face figure {s}	Edge figure {r,s}	Vertex figure {q,r,s}	Dual
Order-5 5-cell honeycomb	{3,3,3,5}	{3,3,3}	{3,3}	{3}	{5}	{3,5}	{3,3,5}	{5,3,3,3}
120-cell honeycomb	{5,3,3,3}	{5,3,3}	{5,3}	{5}	{3}	{3,3}	{3,3,3}	{3,3,3,5}
Order-5 tesseractic honeycomb	{4,3,3,5}	{4,3,3}	{4,3}	{4}	{5}	{3,5}	{3,3,5}	{5,3,3,4}
Order-4 120-cell honeycomb	{5,3,3,4}	{5,3,3}	{5,3}	{5}	{4}	{3,4}	{3,3,4}	{4,3,3,5}
Order-5 120-cell honeycomb	{5,3,3,5}	{5,3,3}	{5,3}	{5}	{5}	{3,5}	{3,3,5}	Self-dual

The two paracompact regular H⁴ honeycombs are: {3,4,3,4}, {4,3,4,3}.

Name	Schläfli Symbol {p,q,r,s}	Facet type {p,q,r}	Cell type {p,q}	Face type {p}	Face figure {s}	Edge figure {r,s}	Vertex figure {q,r,s}	Dual
Order-4 24-cell honeycomb	{3,4,3,4}	{3,4,3}	{3,4}	{3}	{4}	{3,4}	{4,3,4}	{4,3,4,3}
Cubic honeycomb honeycomb	{4,3,4,3}	{4,3,4}	{4,3}	{4}	{3}	{4,3}	{3,4,3}	{3,4,3,4}

There are four regular star-honeycombs in H⁴ space:

Name	Schläfli Symbol {p,q,r,s}	Facet type {p,q,r}	Cell type {p,q}	Face type {p}	Face figure {s}	Edge figure {r,s}	Vertex figure {q,r,s}	Dual
Small stellated 120-cell honeycomb	{5/2,5,3,3}	{5/2,5,3}	{5/2,5}	{5}	{5}	{3,3}	{5,3,3}	{3,3,5,5/2}
Pentagrammic-order 600-cell honeycomb	{3,3,5,5/2}	{3,3,5}	{3,3}	{3}	{5/2}	{5,5/2}	{3,5,5/2}	{5/2,5,3,3}
Order-5 icosahedral 120-cell honeycomb	{3,5,5/2,5}	{3,5,5/2}	{3,5}	{3}	{5}	{5/2,5}	{5,5/2,5}	{5,5/2,5,3}
Great 120-cell honeycomb	{5,5/2,5,3}	{5,5/2,5}	{5,5/2}	{5}	{3}	{5,3}	{5/2,5,3}	{3,5,5/2,5}

Tessellations of hyperbolic 5-space

There are 5 regular honeycombs in H⁵, all paracompact, which include infinite (Euclidean) facets or vertex figures: {3,4,3,3,3}, {3,3,4,3,3}, {3,3,3,4,3}, {3,4,3,3,4}, and {4,3,3,4,3}.

There are no compact regular tessellations of hyperbolic space of dimension 5 or higher and no paracompact regular tessellations in hyperbolic space of dimension 6 or higher.

Name	Schläfli Symbol {p,q,r,s,t}	Facet type {p,q,r,s}	4-face type {p,q,r}	Cell type {p,q}	Face type {p}	Cell figure {t}	Face figure {s,t}	Edge figure {r,s,t}	Vertex figure {q,r,s,t}	Dual
5-orthoplex honeycomb	{3,3,3,4,3}	{3,3,3,4}	{3,3,3}	{3,3}	{3}	{3}	{4,3}	{3,4,3}	{3,3,4,3}	{3,4,3,3,3}
24-cell honeycomb honeycomb	{3,4,3,3,3}	{3,4,3,3}	{3,4,3}	{3,4}	{3}	{3}	{3,3}	{3,3,3}	{3,3,3,3}	{3,3,3,4,3}
16-cell honeycomb honeycomb	{3,3,4,3,3}	{3,3,4,3}	{3,3,4}	{3,3}	{3}	{3}	{3,3}	{4,3,3}	{3,4,3,3}	self-dual
Order-4 24-cell honeycomb honeycomb	{3,4,3,3,4}	{3,4,3,3}	{3,4,3}	{3,4}	{3}	{4}	{3,4}	{3,3,4}	{4,3,3,4}	{4,3,3,4,3}
Tesseractic honeycomb honeycomb	{4,3,3,4,3}	{4,3,3,4}	{4,3,3}	{4,3}	{4}	{3}	{4,3}	{3,4,3}	{3,3,4,3}	{3,4,3,3,4}

Tessellations of hyperbolic 6-space and higher

Even allowing for infinite (Euclidean) facets and/or vertex figures, there are no regular compact or paracompact tessellations of hyperbolic space of dimension 6 or higher.

Apeirotopes

An apeirotope is, like any other polytope, an unbounded hyper-surface. The difference is that whereas a polytope's hyper-surface curls back on itself to close round a finite volume of hyperspace, an apeirotope does not curl back.

Some people regard apeirotopes as just a special kind of polytope, while others regard them as rather different things.

Two dimensions

A regular apeirogon is a regular division of an infinitely long line into equal segments, joined by vertices. It has regular embeddings in the plane, and in higher-dimensional spaces. In two dimensions it can form a straight line or a zig-zag. In three dimensions, it traces out a helical spiral. The zig-zag and spiral forms are said to be skew.

Three dimensions

An apeirohedron is an infinite polyhedral surface. Like an apeirogon, it can be flat or skew. A flat apeirohedron is just a tiling of the plane. A skew apeirohedron is an intricate honeycomb-like structure which divides space into two regions.

There are thirty regular apeirohedra in Euclidean space. These include the tessellations of type {4,4}, {6,3}, {3,6} above, as well as (in the plane) polytopes of type: {∞,3}, {∞,4}, {∞,6} and in 3-dimensional space, blends of these with either an apeirogon or a line segment, and the "pure" 3-dimensional apeirohedra (12 in number)

See also regular skew polyhedron.

Abstract polytopes

The abstract polytopes arose out of an attempt to study polytopes apart from the geometrical space they are embedded in. They include the tessellations of spherical, euclidean and hyperbolic space, tessellations of other manifolds, and many other objects that do not have a well-defined topology, but instead may be characterised by their "local" topology. There are infinitely many in every dimension. See this atlas for a sample. Some notable examples of abstract polytopes that do not appear elsewhere in this list are the 11-cell and the 57-cell.

See also

• Polygon
  • Regular polygon
  • Star polygon
• Polyhedron
  • Regular polyhedron (5 regular Platonic solids and 4 Kepler–Poinsot solids)
    • Uniform polyhedron
• 4-polytope
  • regular 4-polytope (16 regular 4-polytopes, 4 convex and 10 star (Schläfli–Hess))
  • Uniform 4-polytope
• Tessellation
  • Tilings of regular polygons
  • Convex uniform honeycomb
• Regular polytope
  • Uniform polytope

References

• Coxeter, H. S. M. (1956), "Regular honeycombs in hyperbolic space", Proceedings of the International Congress of Mathematicians, 1954, Amsterdam, vol. III (PDF), Amsterdam: North-Holland Publishing Co., pp. 155–169, MR 0087114. Reprinted in Coxeter, H. S. M. (1999), The Beauty of Geometry: Twelve Essays, Mineola, NY: Dover Publications, Inc., Chapter 10, pp. 199–214, ISBN 0-486-40919-8, MR 1717154. See in particular Summary Tables II,III,IV,V, pp. 212–213 of The Beauty of Geometry.
• Coxeter, H. S. M. (1973), Regular Polytopes (Third ed.), New York: Dover Publications, Inc., MR 0370327. See in particular Tables I and II: Regular polytopes and honeycombs, pp. 294–296.
• Johnson, Norman W. (2012), "Regular inversive polytopes" (PDF), International Conference on Mathematics of Distances and Applications (July 2–5, 2012, Varna, Bulgaria), pp. 85–95 Paper 27
• McMullen, Peter; Schulte, Egon (2002), Abstract Regular Polytopes, Encyclopedia of Mathematics and its Applications, vol. 92, Cambridge: Cambridge University Press, doi:10.1017/CBO9780511546686, ISBN 0-521-81496-0, MR 1965665
• Sommerville, D. M. Y. (1958), An Introduction to the Geometry of n Dimensions, New York: Dover Publications, Inc., MR 0100239. Reprint of 1930 ed., published by E. P. Dutton. See in particular Chapter X: The Regular Polytopes.

External links

• The Platonic Solids
• Kepler-Poinsot Polyhedra
• Regular 4d Polytope Foldouts
• Multidimensional Glossary (Look up Hexacosichoron and Hecatonicosachoron)
• Polytope Viewer
• Polytopes and optimal packing of p points in n dimensional spheres
• An atlas of small regular polytopes

Fundamental convex regular and uniform honeycombs in dimensions 2–9
Space	Family	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
E2	Uniform tiling	0[3]	δ3	hδ3	qδ3	Hexagonal
E3	Uniform convex honeycomb	0[4]	δ4	hδ4	qδ4
E4	Uniform 4-honeycomb	0[5]	δ5	hδ5	qδ5	24-cell honeycomb
E5	Uniform 5-honeycomb	0[6]	δ6	hδ6	qδ6
E6	Uniform 6-honeycomb	0[7]	δ7	hδ7	qδ7	222
E7	Uniform 7-honeycomb	0[8]	δ8	hδ8	qδ8	133 • 331
E8	Uniform 8-honeycomb	0[9]	δ9	hδ9	qδ9	152 • 251 • 521
E9	Uniform 9-honeycomb	0[10]	δ10	hδ10	qδ10
E10	Uniform 10-honeycomb	0[11]	δ11	hδ11	qδ11
En-1	Uniform (n-1)-honeycomb	0[n]	δn	hδn	qδn	1k2 • 2k1 • k21