Oblique lattice
Appearance

|

|
|
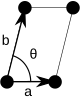
| Oblique lattice | Wallpaper group p2 | Unit cell |
|---|
The oblique lattice is one of the five two-dimensional Bravais lattice types.[1] The symmetry category of the lattice is wallpaper group p2. The primitive translation vectors of the oblique lattice form an angle other than 90° and are of unequal lengths.
Crystal classes
[edit]The oblique lattice class names, Schönflies notation, Hermann-Mauguin notation, orbifold notation, Coxeter notation, and wallpaper groups are listed in the table below.
| Geometric class, point group | Arithmetic class |
Wallpaper groups | ||||
|---|---|---|---|---|---|---|
| Schön. | Intl | Orb. | Cox. | |||
| C1 | 1 | (1) | [ ]+ | None | p1 (1) | |
| C2 | 2 | (22) | [2]+ | None | p2 (2222) | |
References
[edit]- ^ Rana, Farhan. "Lattices in 1D, 2D, and 3D" (PDF). Cornell University. Archived (PDF) from the original on 2020-12-18.
