Wild arc
In geometric topology, a wild arc is an embedding of the unit interval into 3-dimensional space not equivalent to the usual one in the sense that there does not exist an ambient isotopy taking the arc to a straight line segment. Antoine (1920) found the first example of a wild arc, and Fox & Artin (1948) found another example called the Fox-Artin arc whose complement is not simply connected.
Fox-Artin arcs
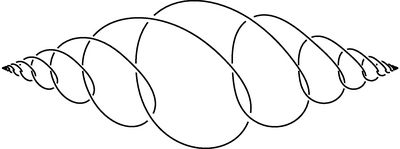
Two very similar wild arcs appear in the Fox & Artin (1948). Example 1.1 is most generally referred to as the Fox-Artin wild arc. The crossings have the regular sequence over/over/under/over/under/under when following the curve from left to right.
The left end-point 0 of the closed unit interval is mapped by the arc to the left limit point of the curve, and 1 is mapped to the right limit point. The range of the arc lies in the Euclidean space or the 3-sphere .
Fox-Artin arc variant

Example 1.1* has the crossing sequence over/under/over/under/over/under. According to Fox & Artin (1948), page 982: "This is just the chain stitch of knitting extended indefinitely in both directions."
This arc cannot be continuously deformed in or to produce Example 1.1, despite its similar appearance.

Also shown here is an alternative style of diagram for the arc in Example 1.1*.
See also
Further reading
- Antoine, L. (1920), "Sur la possibilité d'étendre l'homéomorphie de deux figures à leurs voisinages", C. R. Acad. Sci. Paris (in French), 171: 661
- Fox, Ralph H.; Harrold, O. G. (1962), "The Wilder arcs", Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), Prentice Hall, pp. 184–187, MR 0140096
- Fox, Ralph H.; Artin, Emil (1948), "Some wild cells and spheres in three-dimensional space", Annals of Mathematics, Second Series, 49 (4): 979–990, doi:10.2307/1969408, ISSN 0003-486X, JSTOR 1969408, MR 0027512
- Hocking, John Gilbert; Young, Gail Sellers (1988) [1961]. Topology. Dover. pp. 176–177. ISBN 0-486-65676-4.
- McPherson, James M. (1973), "Wild arcs in three-space. I. Families of Fox–Artin arcs", Pacific Journal of Mathematics, 45 (2): 585–598, doi:10.2140/pjm.1973.45.585, ISSN 0030-8730, MR 0343276

![{\displaystyle [0,1]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)


