Young tableau

In mathematics, a Young tableau is a combinatorial object useful in representation theory. It provides a convenient way to describe the group representations of the symmetric group and to study their properties.

Young tableaux were introduced by Alfred Young, a mathematician at Cambridge University, in 1900. They were then applied to the study of symmetric group by Georg Frobenius in 1903. The theory was further developed by Alfred Young, and by other mathematicians including Alain Lascoux, Percy MacMahon, G. de B. Robinson, Gian-Carlo Rota, Marcel-Paul Schützenberger and Richard P. Stanley.

Definitions

Young diagram

A Young diagram

A Young diagram (also called Ferrers diagram) is a way to represent partitions of a number n. Let n be a natural number. A partition is a way of expressing n as a sum of natural numbers: n = k₁ + k₂ + ... + k_m, where k₁ ≥ k₂ ≥ .... A partition can be described by a Young diagram which consists of m rows, with the first row containing k₁ boxes, the second row containing k₂ boxes, etc. Each row is left-justified.

Let's call this partition k (dropping the subscript, but remembering that it is there). Then the partition conjugate to k is the partition of n consisting of the count of boxes in each column. That is, for each Young diagram, there is a conjugate diagram which has the horizontal and vertical reflected across the diagonal.

The figure on the right shows the Young diagram corresponding to the partition 10 = 5 + 4 + 1. The conjugate partition is 10 = 3 + 2 + 2 + 2 + 1.

Young tableau

A Young tableau

A Young tableau is obtained by taking a Young diagram and writing numbers 1, 2, ..., n into n boxes of this diagram, subject to the following constraints:

• in each row, the numbers must be increasing from left to right;
• in each column, the numbers must be increasing from top to bottom.

If each number appears in exactly one square, the tableau is called a standard tableau. The figure on the right shows one of the standard Young tableaux for the partition 10 = 5 + 4 + 1.

Semi-standard tableaux are a variant of this object in which a number can appear in more than one square (with multiplicity greater than one). For semi-standard tableaux, the first constraint above is weakened:

• in each row, the numbers must be nondecreasing from left to right.

A semi-standard tableau may have any entries 1, 2, ..., t, where t is usually explicitly specified. Not all numbers from the set 1, 2, ..., t need to appear in a semi-standard Young tableaux, and some may appear more than once. Because the numbers need to increase in columns, we must have $t\geq m$ in order for the semi-standard Young tableaux to exist.

Applications in representation theory

Young diagrams are in one-to-one correspondence with irreducible representations of the symmetric group over the complex numbers. They provide a convenient way of specifying the Young symmetrizers from which the irreducible representations are built. Many facts about a representation can be deduced from the corresponding diagram. Below, we describe two examples: determining the dimension of a representation and restricted representations. In both cases, we will see that some properties of a representation can be determined by using just its diagram.

Dimension of a representation

Hook lengths

The dimension of the irreducible representation $\pi _{\lambda }$ corresponding to a partition $\lambda$ is equal to the number of different Young tableaux that can be obtained from the diagram of the representation. This number can be calculated by hook-length formula.

A hook length $\operatorname {hook} (x)$ of a box $x$ in Young diagram $\lambda$ is the number of boxes that are in the same row to the right of it plus those boxes in the same column below it, plus one (for the box itself). By the hook-length formula, the dimension of an irreducible representation is n! divided by the product of the hook lengths of all boxes in the diagram of the representation:

${\rm {dim}}\,\pi _{\lambda }={\frac {n!}{\prod _{x\in \lambda }{\rm {hook}}(x)}}.$

The figure on the right shows hook-lengths for all boxes in the diagram of the partition 10 = 5 + 4 + 1. Thus ${\rm {dim}}\,\pi _{\lambda }={\frac {10!}{1\cdot 1\cdot 1\cdot 2\cdot 3\cdot 3\cdot 4\cdot 5\cdot 5\cdot 7}}=288$.

Restricted representations

A representation of the symmetric group on n elements, S_n is also a representation of the symmetric group on n − 1 elements, S_n−1. However, an irreducible representation of S_n may not be irreducible for S_n−1. Instead, it may be a direct sum of several representations that are irreducible for S_n−1. These representations are then called restricted representations (see also induced representations). The problem is to determine the restricted representations, given a Young diagram for the representation of S_n.

The answer is that the restricted representations are exactly the ones with Young diagrams which can be obtained by deleting one square from the Young diagram of the representation of S_n so that the result is still a valid diagram.

Young tableaux for SU(N) with Examples

Connection between Young Tableaux and Dynkin numbers

Given a representation R of G=SU(N) with Dynkin indexes (q₁ ...,q_k,.. q_N-1) its Young tableaux consists of N-1 blocks each of k rows and q_k columns. Therefore in SU(3) the adjoint has Dynkin numbers (1,1) and its tableeaux is made of one block of one column and one row (since q₁=1) and a block of two rows and one column (since q₂=1). On the same footing you can find the result for (2,0) and (0,1), that are usually called the 6 and the 3* representations of SU(3).

Symmetry Structure of a n-index tensor (representation) of SU(N)

A Tableau is a way to encode the symmetry structure of a representation. Assigning an index to each box we can link a n-box tableau to a n-index tensor. This tensor will be antisymmetric under the exchange of indexes belonging to the same column of the tableau and symmetric under the exchange of two indexes belonging to the same row of the tableau.

Multiplication Rule of Tableaux

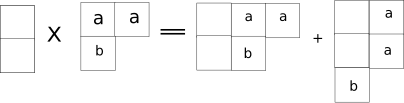
The multiplication of Tableaux A and B, AxB, happen on the same footing of what shown before. You label each box in the first row one of the tableaux with the a letter, which the representative of an index of the tensor the tableau stands for. Say you label the first row of the tableau B with the letter a. The you label the second row with the letter "b" and so on. Once you have labelled all the row the tableau B, you start building on the tableau A. You build first placing the a-s of the first row then the b's then the c's. The only rule you have to follow is that the resulting tableaux, at each stage, must have a number of boxes in each row which is greater or equal as you go from the last row to the first. The other rule is that in each row the number of a must be greater of the number of b.

Conservation of the n-ality

For SU(N) a column of N boxes represent an antisymmetrization of N indexes, therefore it corresponds to the ε tensor. This tensor is an invriant, therefore does not change the structure of the tensor the tableau represent. Thus you can delete all the columns with N boxes which appear in the tableau. For this reason in the product of tableaux A and B, with A made of i boxes and B made of k boxes,

i+k mod(N)

is the same in each term of the product. This is the consevation of the N-ality (i.e. triality for SU(3) and so and so forth).

Dimension of the representation

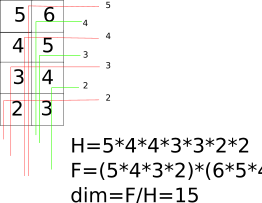
Computation of the dimension of the representation the tableau stands for is done by filling the boxes with numbers. For SU(N) you place N in the upper-left box. Then you fill the first row with N+1, N+2 ... and the first column with N-1, N-2, ... This will result in something like the picture. Then you compute the hook factor H and the tableau factor F. A hook is a path into the tableau which is straight and then turn right. A hook cross each box zero or one time. Each hook has a hook-factor which amounts to the number of boxes it cross. H is the product of all the possible hook factors. F is just the multiplication of the all the numbers you used to fill the tableaux. The dimension of the representation is

dim=F/H

Complex Conjugation of a Tableaux

For SU(N) the representation R and R* have Young Tableaux which can be assembled in a rectangle of height N by mean of a rigid rotation of one of the two tableaux. Some example for SU(5) is provided in the picture. Notice for instance that the 24, which is the adjoint and therefore real, has the same tableau of the 24*.

Branching Rules with Young Tableaux

Young Tableaux can also be used to find how a representation R of the SU(N) transform as representation of the subgroup H. See Georgi for details.

Extensively Expanded Examples

Young tableaux can be used to compute the multiplications
3x3*=u^k v_i = 8+1 with
8=v_iu^k-1/3 δ_k^mv_mu^k
1=1/3 u_kv^k
6x3=10+8
Branching rules
3->2+1
8->3+2+2+1

See also

• Robinson-Schensted algorithm
• Partition (number theory)

References

• William Fulton. Young Tableaux, with Applications to Representation Theory and Geometry. Cambridge University Press, 1997, ISBN 0521567246.
• William Fulton and Joe Harris, Representation Theory, A First Course (1991) Springer Verlag New York, ISBN 0-387-97495-4 See Chapter 4
• Bruce E. Sagan. The Symmetric Group. Springer, 2001, ISBN 0387950672
• Eric W. Weisstein. "Ferrers Diagram". From MathWorld--A Wolfram Web Resource.
• Eric W. Weisstein. "Young Tableau." From MathWorld--A Wolfram Web Resource.
• Jean-Christophe Novelli, Igor Pak, Alexander V. Stoyanovkii, "A direct bijective proof of the Hook-length formula", Discrete Mathematics and Theoretical Computer Science 1 (1997), pp.53–67.
• Howard Georgi, Lie Algebras in Particle Physics, 2nd Edition - Westview