Natural logarithm

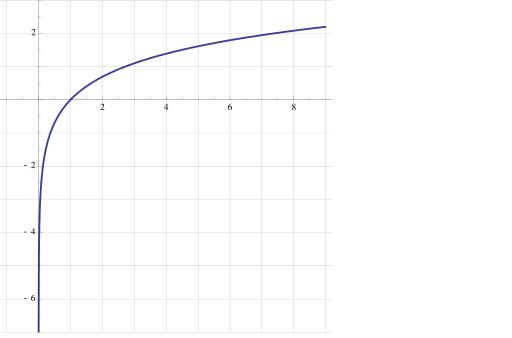
The natural logarithm, formerly known as the hyperbolic logarithm, is the logarithm to the base e, where $e$ is an irrational constant approximately equal to 2.718281828459. In simple terms, the natural logarithm of a number $x$ is the power to which $e$ would have to be raised to equal $x$ — for example the natural log of $e$ itself is 1 because $e^{1}=e$ , while the natural logarithm of 1 would be 0, since $e^{0}=1$ . The natural logarithm can be defined for all positive real numbers x as the area under the curve $y=1/t$ from 1 to $x$ , and can also be defined for non-zero complex numbers as explained below.

The natural logarithm function can also be defined as the inverse function of the exponential function, leading to the identities:

e^{\ln(x)}=x\qquad {\mbox{if }}x>0\,\!

\ln(e^{x})=x.\,\!

In other words, the logarithm function is a bijection from the set of positive real numbers to the set of all real numbers. More precisely it is an isomorphism from the group of positive real numbers under multiplication to the group of real numbers under addition. Represented as a function:

\ln :\mathbb {R} ^{+}\to \mathbb {R}

Logarithms can be defined to any positive base other than 1, not just $e$ , and are useful for solving equations in which the unknown appears as the exponent of some other quantity.

Notational conventions

Mathematicians, statisticians, and some engineers generally understand either " $\log(x)$ " or " $\ln(x)$ " to mean $\log _{e}(x)$ , i.e., the natural logarithm of $x$ , and write " $log_{10}(x)$ " if the [[common logarithm|base-10 logarithm]] of $x$ is intended.

Some engineers, biologists, and some others generally write " $\ln(x)$ " (or occasionally " $\log _{e}(x)$ ") when they mean the natural logarithm of $x$ , and take " $\log(x)$ " to mean [[common logarithm| $log_{10}$ ]] $(x)$ or, in the case of some computer scientists, [[binary logarithm| $log_{2}$ ]] $(x)$ .

In most commonly-used programming languages, including C, C++, Fortran, and BASIC, "log" or "LOG" refers to the natural logarithm.

In hand-held calculators, the natural logarithm is denoted ln, whereas log is the base-10 logarithm.

Why it is called “natural”

Initially, it might seem that since our numbering system is [[base 10]], this base would be more “natural” than base $e$ . $\log _{e}$ is a “natural” log because it automatically springs from, and appears so often, in mathematics.

For example, consider the problem of differentiating a logarithmic function:

{\frac {d}{dx}}\log _{b}(x)={\frac {\log _{b}e}{x}}

If the base $b$ equals $e$ , then the derivative is simply $1/x$ , and at $x=1$ this derivative equals 1. Another sense in which the base- $e$ logarithm is the most natural is that it can be defined quite easily in terms of a simple integral or Taylor series and this is not true of other logarithms.

Further senses of this naturalness make no use of calculus. As an example, there are a number of simple series involving the natural logarithm. In fact, Pietro Mengoli and Nicholas Mercator called it logarithmus naturalis a few decades before Newton and Leibniz developed calculus.^[1]

Definitions

Formally, $\ln(a)$ may be defined as the area under the graph (integral) of $1/x$ from 1 to $a$ , that is,

\ln(a)=\int _{1}^{a}{\frac {1}{x}}\,dx.

This defines a logarithm because it satisfies the fundamental property of a logarithm:

\ln(ab)=\ln(a)+\ln(b)\,\!

This can be demonstrated by letting $t={\tfrac {x}{a}}$ as follows:

\ln(ab)=\int _{1}^{ab}{\frac {1}{x}}\;dx=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{a}^{ab}{\frac {1}{x}}\;dx=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{1}^{b}{\frac {1}{t}}\;dt=\ln(a)+\ln(b)

The number e can then be defined as the unique real number $a$ such that $\ln(a)=1$ .

Alternatively, if the exponential function has been defined first using an infinite series, the natural logarithm may be defined as its inverse function, i.e., $\ln(x)$ is that function such that $e^{\ln(x)}=x\!$ . Since the range of the exponential function on real arguments is all positive real numbers and since the exponential function is strictly increasing, this is well-defined for all positive $x$ .

Derivative, Taylor series

The derivative of the natural logarithm is given by

{\frac {d}{dx}}\ln(x)={\frac {1}{x}}.\,

This leads to the Taylor series

\ln(1+x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots \quad {\rm {for}}\quad \left|x\right|\leq 1\quad {\rm {unless}}\quad x=-1

which is also known as the Mercator series.

Substituting $x-1$ for $x$ , we obtain an alternative form for $\ln x$ itself, namely

\ln(x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}(x-1)^{n}=(x-1)-{\frac {(x-1)^{2}}{2}}+{\frac {(x-1)^{3}}{3}}-{\frac {(x-1)^{4}}{4}}\cdots

{\rm {for}}\quad \left|x-1\right|\leq 1\quad {\rm {unless}}\quad x=0.

^[2]

By using the Euler transform on the Mercator series, one obtains the following, which is valid for any $x$ with absolute value greater than 1:

\ln {x \over {x-1}}=\sum _{n=1}^{\infty }{1 \over {nx^{n}}}={1 \over x}+{1 \over {2x^{2}}}+{1 \over {3x^{3}}}+\cdots

This series is similar to a BBP-type formula.

Also note that $x \over {x-1}$ is its own inverse function, so to yield the natural logarithm of a certain number n, simply put in $n \over {n-1}$ for $x$ .

The natural logarithm in integration

The natural logarithm allows simple integration of functions of the form $\scriptstyle g(x)=f'(x)/f(x)$ : an antiderivative of $g(x)$ is given by $\ln |f(x)|$ . This is the case because of the chain rule and the following fact:

\ {d \over dx}\left(\ln \left|x\right|\right)={1 \over x}.

In other words,

\int {1 \over x}dx=\ln |x|+C

and

\int {{\frac {f'(x)}{f(x)}}\,dx}=\ln |f(x)|+C.

Here is an example in the case of $g(x)=\tan(x)$ :

\int \tan(x)\,dx=\int {\sin(x) \over \cos(x)}\,dx

\int \tan(x)\,dx=\int {-{d \over dx}\cos(x) \over {\cos(x)}}\,dx.

Letting $\scriptstyle f(x)=\cos(x)$ and $\scriptstyle f'(x)=-\sin(x)$ :

\int \tan(x)\,dx=-\ln {\left|\cos(x)\right|}+C

\int \tan(x)\,dx=\ln {\left|\sec(x)\right|}+C

where $C$ is an arbitrary constant of integration.

The natural logarithm can be integrated using integration by parts:

\int \ln(x)\,dx=x\ln(x)-x+C.

Numerical value

To calculate the numerical value of the natural logarithm of a number, the Taylor series expansion can be rewritten as:

\ln(1+x)=x\,\left({\frac {1}{1}}-x\,\left({\frac {1}{2}}-x\,\left({\frac {1}{3}}-x\,\left({\frac {1}{4}}-x\,\left({\frac {1}{5}}-\ldots \right)\right)\right)\right)\right)\quad {\rm {for}}\quad \left|x\right|<1.

To obtain a better rate of convergence, the following identity can be used.

{\begin{aligned}\ln(x)=\ln \left({\frac {1+y}{1-y}}\right)&=2\,y\,\left({\frac {1}{1}}+{\frac {1}{3}}y^{2}+{\frac {1}{5}}y^{4}+{\frac {1}{7}}y^{6}+{\frac {1}{9}}y^{8}+\ldots \right)\\&=2\,y\,\left({\frac {1}{1}}+y^{2}\,\left({\frac {1}{3}}+y^{2}\,\left({\frac {1}{5}}+y^{2}\,\left({\frac {1}{7}}+y^{2}\,\left({\frac {1}{9}}+\ldots \right)\right)\right)\right)\right)\end{aligned}}

provided that

y=(x-1)/(x+1)

and

x>0

.

For $\ln(x)$ where $x>1$ , the closer the value of $x$ is to 1, the faster the rate of convergence. The identities associated with the logarithm can be leveraged to exploit this:

{\begin{aligned}\ln(123.456)&=\ln(1.23456\times 10^{2})\\&=\ln(1.23456)+\ln(10^{2})\\&=\ln(1.23456)+2\times \ln(10)\\&\approx \ln(1.23456)+2\times 2.3025851\end{aligned}}

Such techniques were used before calculators, by referring to numerical tables and performing manipulations such as those above.

High precision

To compute the natural logarithm with many digits of precision, the Taylor series approach is not efficient since the convergence is slow. An alternative is to use Newton's method to invert the exponential function, whose series converges more quickly.

An alternative for extremely high precision calculation is the formula ^{[citation needed]}

\ln x\approx {\frac {\pi }{2M(1,4/s)}}-m\ln 2

where $M$ denotes the arithmetic-geometric mean and

s=x\,2^{m}>2^{p/2},

with $m$ chosen so that $p$ bits of precision is attained. In fact, if this method is used, Newton inversion of the natural logarithm may conversely be used to calculate the exponential function efficiently. (The constants $\ln 2$ and $\Pi$ can be pre-computed to the desired precision using any of several known quickly converging series.)

Computational complexity

The computational complexity of computing the natural logarithm (using the arithmetic-geometric mean) is $\mathrm {O} (M(n)\ln n)$ . Here $n$ is the number of digits of precision at which the natural logarithm is to be evaluated and $M(n)$ is the computational complexity of multiplying two $n$ -digit numbers.

Complex logarithms

The exponential function can be extended to a function which gives a complex number as $e^{x}$ for any arbitrary complex number $x$ ; simply use the infinite series with $x$ complex. This exponential function can be inverted to form a complex logarithm that exhibits most of the properties of the ordinary logarithm. There are two difficulties involved: no $x$ has $e^{x}=0$ ; and it turns out that $e^{2\pi i}=1=e^{0}$ . Since the multiplicative property still works for the complex exponential function, $e^{z}=e^{z+2n\pi i}$ , for all complex $z$ and integers $n$ .

So the logarithm cannot be defined for the whole complex plane, and even then it is multi-valued – any complex logarithm can be changed into an "equivalent" logarithm by adding any integer multiple of $2\pi i$ at will. The complex logarithm can only be single-valued on the cut plane. For example, $\ln i=1/2\pi i$ or $5/2\pi i$ or $-3/2\pi i$ , etc.; and although $i^{4}=1$ , $4\log i$ can be defined as $2\pi i$ , or $10\pi i$ or $-6\pi i$ , and so on.