Jump to content

Analytic hierarchy process

From Wikipedia, the free encyclopedia

This is an old revision of this page, as edited by MathDame (talk | contribs) at 03:06, 15 February 2008 (→Criticisms: Changed wording to more accurately reflect how it is phrased in the reference. See talk.). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

The Analytic Hierarchy Process (AHP) is a structured technique for dealing with complex decisions. Based on mathematics and human psychology, it was developed by Thomas L. Saaty in the 1970s and has been extensively studied and refined since then. The AHP provides a comprehensive and rational framework for structuring a problem, for representing and quantifying its elements, for relating those elements to overall goals, and for evaluating alternative solutions. It is used throughout the world in a wide variety of decision situations, in fields such as government, business, industry, healthcare, and education.

Several firms supply computer software to assist in applying the process.

Users of the AHP first decompose their decision problem into a hierarchy of more easily comprehended sub-problems, each of which can be analyzed independently. The elements of the hierarchy can relate to any aspect of the decision problem—tangible or intangible, carefully measured or roughly estimated, well- or poorly-understood—anything at all that applies to the decision at hand.

Once the hierarchy is built, the decision makers systematically evaluate its various elements, comparing them to one another in pairs. In making the comparisons, the decision makers can use concrete data about the elements, or they can use their judgments about the elements' relative meaning and importance. It is the essence of the AHP that human judgments, and not just the underlying information, can be used in performing the evaluations.

The AHP converts these evaluations to numerical values that can be processed and compared over the entire range of the problem. A numerical weight or priority is derived for each element of the hierarchy, allowing diverse and often incommensurable elements to be compared to one another in a rational and consistent way. This capability distinguishes the AHP from other decision making techniques.

In the final step of the process, numerical priorities are derived for each of the decision alternatives. Since these numbers represent the alternatives' relative ability to achieve the decision goal, they allow a straightforward consideration of the various courses of action.

Uses and applications

While it can be used by individuals working on straightforward decisions, AHP is most useful where teams of people are working on complex problems, especially those with high stakes, involving human perceptions and judgments, whose resolutions have long-term repercussions.[1] It has unique advantages where important elements of the decision are difficult to quantify or compare, or where communication among team members is impeded by their different specializations, terminologies, or perspectives.

The applications of AHP to complex decision situations have numbered in the thousands,[2] and have produced extensive results in problems involving alternative selection, planning, resource allocation, and priority setting.[1] Many such applications are never reported to the world at large, because they take place at high levels of large organizations where security and privacy considerations prohibit their disclosure. But some uses of AHP are discussed in the literature. Recently these have included:

AHP was recently applied to a project that uses video footage to assess the condition of highways in Virginia. Highway engineers first used it to determine the optimum scope of the project, then to justify its budget to lawmakers.[8]

The process is widely used in countries around the world. At a recent international conference on AHP, over 90 papers were presented from 19 countries, including the U.S., Germany, Japan, Chile, Malaysia, and Nepal. Topics covered ranged from Establishing Payment Standards for Surgical Specialists, to Strategic Technology Roadmapping, to Infrastructure Reconstruction in Devastated Countries.[9] AHP was introduced in China in 1982, and its use in that country has expanded greatly since then—its methods are highly compatible with the traditional Chinese decision making framework, and it has been used for many decisions in the fields of economics, energy, management, environment, traffic, agriculture, industry, and the military.[10]

Though using AHP requires no specialized academic training, the subject is widely taught at the university level—one AHP software provider lists over a hundred colleges and universities among its clients.[11] AHP is considered an important subject in many institutions of higher learning, including schools of engineering[12] and graduate schools of business.[13] AHP is also an important subject in the quality field, and is taught in many specialized courses including Six Sigma, Lean Six Sigma, and QFD.[14][15][16]

In China, nearly a hundred schools offer courses in AHP, and many doctoral students choose AHP as the subject of their research and dissertations. Over 900 papers have been published on the subject in that country, and there is at least one Chinese scholarly journal devoted exclusively to AHP.[10]

Summary

The procedure can be summarized as:

  1. The alternatives and the significant attributes are identified.
  2. For each attribute, and each pair of alternatives, the decision makers specify their preference (for example, whether the location of alternative "A" is preferred to that of "B") in the form of a fraction between 1/9 and 9.
  3. Decision makers similarly indicate the relative significance of the attributes. For example, if the alternatives are comparing potential real-estate purchases, the investors might say they prefer location over price and price over timing.
  4. Each matrix of preferences is evaluated by using eigenvalues to check the consistency of the responses. This produces a "consistency coefficient" where a value of "1" means all preferences are internally consistent.[citation needed] This value would be lower, however, if a decision maker said X is preferred to Y, Y to Z but Z is preferred to X (such a position is internally inconsistent). It is this step that that causes many users to believe that AHP is theoretically well founded.[citation needed]
  5. A score is calculated for each alternative.

The two basic steps in the process are to model the problem as a hierarchy, then to establish priorities for its elements. These are more fully described below.

Model the problem as a hierarchy

The first step in the Analytic Hierarchy Process is to model the problem as a hierarchy. In doing this, participants explore the aspects of the problem at levels from general to detailed, then express it in the multileveled way that the AHP requires. As they work to build the hierarchy, they increase their understanding of the problem, of its context, and of each other's thoughts and feelings about both.[17]

Hierarchies defined

A hierarchy is a system of ranking and organizing people, things, ideas, etc., where each element of the system, except for the top one, is subordinate to one or more other elements. Diagrams of hierarchies are often shaped roughly like pyramids, but other than having a single element at the top, there is nothing necessarily pyramid-shaped about a hierarchy.

Human organizations are often structured as hierarchies, where the hierarchical system is used for assigning responsibilities, exercising leadership, and facilitating communication. Familiar hierarchies of "things" include a desktop computer's tower unit at the "top," with its subordinate monitor, keyboard, and mouse "below."

In the world of ideas, we use hierarchies to help us acquire detailed knowledge of complex reality: we structure the reality into its constituent parts, and these in turn into their own constituent parts, proceeding down the hierarchy as many levels as we care to. At each step, we focus on understanding a single component of the whole, temporarily disregarding the other components at this and all other levels. As we go through this process, we increase our global understanding of whatever complex reality we are studying.

Think of the hierarchy that medical students use while learning anatomy—they separately consider the musculoskeletal system (including parts and subparts like the hand and its constituent muscles and bones), the circulatory system (and its many levels and branches), the nervous system (and its numerous components and subsystems), etc., until they've covered all the systems and the important subdivisions of each. Advanced students continue the subdivision all the way to the level of the cell or molecule. In the end, the students understand the "big picture" and a considerable number of its details. Not only that, but they understand the relation of the individual parts to the whole. By working hierarchically, they've gained a comprehensive understanding of anatomy.

Similarly, when we approach a complex decision problem, we can use a hierarchy to integrate large amounts of information into our understanding of the situation. As we build this information structure, we form a better and better picture of the problem as a whole.[17]

AHP hierarchies explained

An AHP hierarchy is a structured means of describing the problem at hand. It consists of an overall goal, a group of options or alternatives for reaching the goal, and a group of factors or criteria that relate the alternatives to the goal. In most cases the criteria are further broken down into subcriteria, sub-subcriteria, and so on, in as many levels as the problem requires.

The hierarchy can be visualized as a diagram like the one below, with the goal at the top, the alternatives at the bottom, and the criteria filling up the middle. In such diagrams, each box is called a node. The boxes descending from any node are called its children. The node from which a child node descends is called its parent. Applying these definitions to the diagram below, the six Criteria are children of the Goal, and the Goal is the parent of each of the six Criteria. Each Alternative is the child of each of the Criteria, and each Criterion is the parent of three Alternatives.

A simple AHP hierarchy. In practice, many Criteria have one or more layers of subcriteria. These are not shown in this simplified diagram. Also, to avoid clutter in AHP diagrams, the lines between the Alternatives and Criteria are often omitted or reduced in number. Regardless of any such simplifications in the diagram, in the actual hierarchy each Alternative is connected to every one of its covering criteria—the lowest-level criteria, subcriteria, etc. of which it is a child.

The design of any AHP hierarchy will depend not only on the nature of the problem at hand, but also on the knowledge, judgments, values, opinions, needs, wants, etc. of the participants in the process.

As the AHP proceeds through its other steps, the hierarchy can be changed to accommodate newly-thought-of criteria or criteria not originally considered to be important; alternatives can also be added, deleted, or changed.[17]

A simple example

In an AHP hierarchy for the simple case of buying a vehicle, the goal might be to choose the best car for the Jones family. The family might decide to consider cost, safety, style, and capacity as the criteria for making their decision. They might subdivide the cost criterion into purchase price, fuel costs, maintenance costs, and resale value. They might separate Capacity into cargo capacity and passenger capacity. The family, which for personal reasons always buys Hondas, might decide to consider as alternatives the Accord Sedan, Accord Hybrid Sedan, Pilot SUV, CR-V SUV, Element SUV, and Odyssey Minivan.

The Jones' hierarchy could be diagrammed as shown below:

File:AHPHierarchy2a.png
AHP hierarchy for the Jones family car buying decision. The Goal is green, the Criteria and Subcriteria are yellow, and the Alternatives are pink. All the alternatives (six different models of Hondas) are shown below the lowest level of each criterion. Later in the process, each alternative (each model) will be rated with respect to the criterion or subcriterion directly above it.
Alternatives for the Jones family car buying decision. To save space in the diagrams, we have represented them as stacks of papers.

As they build their hierarchy, the Joneses should investigate the values or measurements of the different elements that make it up. If there are published safety ratings, for example, or manufacturer's specs for cargo capacity, they should be gathered as part of the process. This information will be needed later, when the criteria and alternatives are evaluated. Information about the Jones' alternatives, including color photos, can be found HERE.

Note that the measurements for some criteria, such as purchase price, can be stated with absolute certainty. Others, such as resale value, must be estimated, so must be stated with somewhat less confidence. Still others, such as style, are really in the eye of the beholder and are hard to state quantitatively at all. The AHP can accommodate all these types of criteria, even when they are present in a single problem.

Also note that the structure of the vehicle-buying hierarchy might be different for other families (ones who don't limit themselves to Hondas, or who care nothing about style, or who drive less than 5,000 miles a year, etc.). It would definitely be different for a 25-year-old playboy who doesn't care how much his cars cost, knows he will never wreck one, and is intensely interested in speed, handling, and the numerous aspects of style.[17]

Establish priorities

Once the hierarchy has been constructed, the participants use AHP to establish priorities for all its nodes. In doing so, information is elicited from the participants and processed mathematically. This activity is somewhat complex, and the participants have many options on the road to completing it. This and the following sections describe a simple, straightforward example of establishing priorities.

As our first step, we will define priorities and show how they interact.

Priorities defined

Priorities are numbers associated with the nodes of the hierarchy. By definition, the priority of the Goal is 1.000. The priorities of the Criteria (which are the children of the Goal) can vary in magnitude, but will always add up to 1.000. The priorities of the children of any Criterion can also vary but will always add up to 1.000, as will those of their own children, and so on down the hierarchy.

This illustration shows some priorities for the Jones car buying hierarchy. We'll say more about them in a moment. For now, just observe that the priorities of the children of each parent node add up to 1.000, and that there are three such groups of children in the illustration.

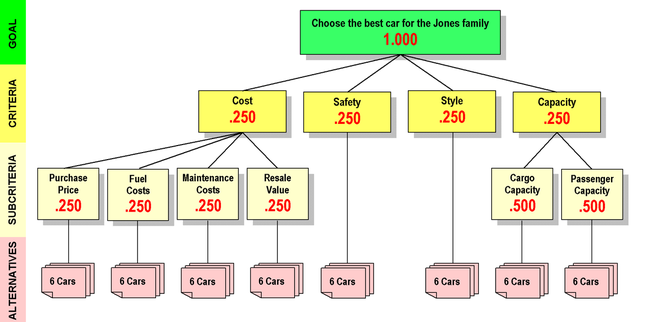
AHP hierarchy for the Jones family car buying decision, with some associated priorities.

If you understand what has been said so far, you will see that if we were to add a "Handling" criterion to this hierarchy, giving it five Criteria instead of four, the priority for each would be .200. You will also know that if the Safety criterion had three children, each of them would have a priority of .333.

In our example as it stands, the priorities within every group of child nodes are equal. In this situation, the priorities are called default priorities. As the analytic hierarchy process continues, the default priorities will change to reflect our judgments about the various items in each group.

As you may have guessed by now, the priorities indicate the relative weights given to the items in a given group of nodes. Depending on the problem at hand, "weight" can refer to importance, or preference, or likelihood, or whatever factor is being considered by the participants.

If all the priorities in a group of nodes are equal, each member of the group has equal weight. If one of the priorities is two times another, or three, (or whatever), that member has two, or three, (or whatever) times the weight of the other one. For example, if we judge cargo capacity to be three times as important as passenger capacity, cargo capacity's new priority will be .750, and passenger capacity's priority will be .250, because .750 = 3 × .250, and .750 + .250 = 1.000. (Don't worry—the AHP software does all this arithmetic automatically .)

AHP priorities have another important feature. The priority of any child node represents its contribution to the priority of its parent. In the diagram above, Cost, Safety, Style and Capacity each contribute .250 of the 1.000 priority of the Goal. Cargo capacity and passenger capacity each contribute half of the priority belonging to the Capacity criterion. Working through the arithmetic, Passenger Capacity contributes .500 × .250 = .125 of the 1.000 priority of the Goal.

As we move ahead through the Analytical Hierarchy Process, the priorities will change but will still add to 1.000 for each group of child nodes.

Criticisms

Although the Analytic Hierarchy Process has been the subject of many research papers and the general consensus is that the technique is both technically valid and practically useful, there are critics of the method.[4] Their criticisms have included: A) since there is no theoretical basis for constructing hierarchies, AHP users can construct different hierarchies for identical decision situations, possibly producing different solutions, B) AHP rankings are claimed to be arbitrary because they are based on subjective opinions using a ratio scale, a situation which can produce "rank reversal," C) there are said to be flaws in the methods of combining individual weights into composite weights, and D) the process has no sound underlying statistical theory.[2] Researchers have found that the flaws in AHP are significant and lead to various types of decision errors (see below).

A series of debates between critics and proponents of AHP have been published in peer reviewed journals, most notably in Management Science[18][19][20][21] and The Journal of the Operations Research Society [22][23][24].

In these debates, AHP critic J. Dyer argues:

"The AHP is flawed as a procedure for ranking alternatives in that the rankings produced by this procedure are arbitrary."[25]

Another AHP critic, R. D. Holder also concludes in 1991 that:

"Thus questions about the validity of AHP are far from having been settled. Also, it is clear that such discussion over a long period has not sufficiently penetrated the AHP users' community, with the result that paper are still being published using a faulty method."[26]

However, even while criticizing AHP, Holder finds room for possible improvement in AHP when he states in the same source:

"No amount of empirical evidence can truly validate a theory with such internal contradictions as the originally constituted AHP, though the theory is a good basis from which to develop."

Of the weaknesses found in AHP, the use of arbitrary scales and certain internal inconsistencies and theoretical flaws have been discussed extensively in the literature.

The use of arbitrary scales

AHP is based on pairwise comparisons where the relative importance of different attributes are given a value on a scale of 1 to 9 or the inverse (1/9th to 1). These values are in practice assigned by verbal elicitation of decision makers. For example, if a person says attribute A is "moderately more imporantant" than attribute B, A is said to have a relative weight of 3 times that of B while being "extremely more important" will give A a weight of 9 times that of B. While this scale is commonly used in AHP, it is arbitrary and alternative scales have been proposed. Empirical research has found "...that the perceived meaning of the verbal expressions varies from one subject to the next and also depends on the set of elements involved in the comparison." [27]. This is a well known result (since the 1930s) from Thurstone's work on attitude scales.[citation needed] However, these researchers felt the problem was correctable in that the scales could be based on empirical evidence of AHP user perceptions.

Inducement of nonexistant order

Another problem is the inducement of "nonexistant order" by innocuous changes even without the addition or deletion of suboptimal alternatives. AHP critic Stan Schenkerman writes in Decision Sciences:

"An apparently unreported problem facing decision makers who use AHP is described [in this paper]. It is demonstrated that conventional AHP and some of its variants (the ideal mode, and the pairwise aggregated approach, PAHAP) can induce ordering even when no order exists. It is also shown that all three approaches can induce different orderings and that the orderings are sensitive to innocuous changes. Thus, even absent addition or deletion of alternatives, the decision maker relying on AHP or these variants can be seriously misled." [28]

Responses by AHP proponents

Proponents argue that in spite of these concerns, the process works well in practice and is extremely popular among decision-makers in the private and public sectors.[29]

See also

Thomas L. Saaty, developer of the Analytic Hierarchy Process.

References

  1. ^ a b Bhushan, Navneet (January, 2004). Strategic Decision Making: Applying the Analytic Hierarchy Process. London: Springer-Verlag. ISBN 1-8523375-6-7. {{cite book}}: Check date values in: |date= (help); Unknown parameter |coauthors= ignored (|author= suggested) (help)
  2. ^ a b c de Steiguer, J.E. (October, 2003), "The Analytic Hierarchy Process as a Means for Integrated Watershed Management" (PDF), in Renard, Kenneth G. (ed.), First Interagency Conference on Research on the Watersheds, Benson, Arizona: U.S. Department of Agriculture, Agricultural Research Service, pp. 736–740, retrieved 2007-08-20 {{citation}}: Check date values in: |date= (help); Unknown parameter |coauthors= ignored (|author= suggested) (help); Unknown parameter |coeditors= ignored (help)
  3. ^ Berrittella, M. (January, 2007), "An Analytic Hierarchy Process for the Evaluation of Transport Policies to Reduce Climate Change Impacts" (PDF), Fondazione Eni Enrico Mattei (Milano), retrieved 2007-08-20 {{citation}}: Check date values in: |date= (help); Cite has empty unknown parameter: |coeditors= (help); Unknown parameter |coauthors= ignored (|author= suggested) (help)
  4. ^ a b McCaffrey, James (June, 2005). "Test Run: The Analytic Hierarchy Process". MSDN Magazine. Retrieved 2007-08-21. {{cite journal}}: Check date values in: |date= (help); Cite has empty unknown parameter: |coauthors= (help)
  5. ^ Grandzol, John R. (August, 2005). "Improving the Faculty Selection Process in Higher Education: A Case for the Analytic Hierarchy Process" (PDF). IR Applications. 6. Retrieved 2007-08-21. {{cite journal}}: Check date values in: |date= (help); Cite has empty unknown parameter: |coauthors= (help)
  6. ^ Atthirawong, Walailak (September, 2002), "An Application of the Analytical Hierarchy Process to International Location Decision-Making" (PDF), in Gregory, Mike (ed.), Proceedings of The 7th Annual Cambridge International Manufacturing Symposium: Restructuring Global Manufacturing, Cambridge, England: University of Cambridge, pp. 1–18, retrieved 2007-08-20 {{citation}}: Check date values in: |date= (help); Unknown parameter |coauthors= ignored (|author= suggested) (help); Unknown parameter |coeditors= ignored (help)CS1 maint: date and year (link)
  7. ^ Dey, Prasanta Kumar (November, 2003). "Analytic Hierarchy Process Analyzes Risk of Operating Cross-Country Petroleum Pipelines in India". Natural Hazards Review. 4 (4): 213–221. Retrieved 2007-08-20. {{cite journal}}: Check date values in: |date= (help); Cite has empty unknown parameter: |coauthors= (help)
  8. ^ Larson, Charles D. (January, 2007), "Application of the Analytic Hierarchy Process to Select Project Scope for Videologging and Pavement Condition Data Collection", 86th Annual Meeting Compendium of Papers CD-ROM, Transportation Research Board of the National Academies, retrieved 2007-08-20 {{citation}}: Check date values in: |date= (help); Cite has empty unknown parameter: |coeditors= (help); Unknown parameter |coauthors= ignored (|author= suggested) (help)
  9. ^ "Participant Names and Papers, ISAHP 2005, Honolulu, Hawaii". July, 2005. Retrieved 2007-08-22. {{cite web}}: Check date values in: |date= (help)
  10. ^ a b Sun, Hongkai (July, 2005), "AHP in China" (PDF), in Levy, Jason (ed.), Proceedings of the 8th International Symposium on the Analytic Hierarchy Process, Honolulu, Hawaii, retrieved 2007-08-20 {{citation}}: Check date values in: |date= (help); Cite has empty unknown parameters: |coeditors= and |coauthors= (help)CS1 maint: date and year (link)
  11. ^ "List of Expert Choice education clients". Retrieved 2007-08-23.
  12. ^ Drake, P.R. (1998). "Using the Analytic Hierarchy Process in Engineering Education" (PDF). International Journal of Engineering Education. 14 (3): 191–196. Retrieved 2007-08-20. {{cite journal}}: Cite has empty unknown parameter: |coauthors= (help)
  13. ^ Bodin, Lawrence (January, 2004). "Exercises for Teaching the Analytic Hierarchy Process". INFORMS Transactions on Education. 4 (2). Retrieved 2007-08-20. {{cite journal}}: Check date values in: |date= (help); Unknown parameter |coauthors= ignored (|author= suggested) (help)
  14. ^ Hallowell, David L. (January, 2005). "Analytical Hierarchy Process (AHP) -- Getting Oriented". iSixSigma.com. Retrieved 2007-08-21. {{cite journal}}: Check date values in: |date= (help); Cite has empty unknown parameter: |coauthors= (help)
  15. ^ "Analytic Hierarchy Process (AHP)". QFD Institute. Retrieved 2007-08-21. {{cite journal}}: Cite has empty unknown parameter: |coauthors= (help)
  16. ^ "Analytical Hierarchy Process: Overview". TheQualityPortal.com. Retrieved 2007-08-21. {{cite journal}}: Cite has empty unknown parameter: |coauthors= (help)
  17. ^ a b c d Saaty, Thomas L. (1999-05-01). Decision Making for Leaders: The Analytic Hierarchy Process for Decisions in a Complex World. Pittsburgh, Pennsylvania: RWS Publications. ISBN 0-9620317-8-X. {{cite book}}: Cite has empty unknown parameter: |coauthors= (help) (This book is the primary source for the sections in which it is cited.)
  18. ^ Dyer, J. S. (1990): Remarks on the Analytic Hierarchy Process. In: Management Science, 36 (3), S. 249-258.
  19. ^ M. V. Mikhalevic "Remarks on the Dyer-Saaty controversy" Cybernetics and Systems Analysis,Volume 30, Number 1 / January, 1994
  20. ^ Patrick T. Harker, Luis G. Vargas, "Reply to 'Remarks on the Analytic Hierarchy Process' by J. S. Dyer", Management Science, Vol. 36, No. 3 (Mar., 1990), pp. 269-273
  21. ^ Dyer, J.S. (1990b), "A clarification of ‘Remarks on the analytic hierarchy process’", Management Science, Vol. 36 No.3, pp.274-5.
  22. ^ Holder, R.D., Some Comment on the Analytic Hierarchy Process, Journal of the Operational Research Society, 1990, 41, 11 1073-1076.
  23. ^ Thomas L. Saaty "Response to Holder's Comments on the Analytic Hierarchy Process" The Journal of the Operational Research Society, Vol. 42, No. 10 (Oct., 1991), pp. 909-914
  24. ^ R. D. Holder "Response to Holder's Comments on the Analytic Hierarchy Process: Response to the Response" The Journal of the Operational Research Society, Vol. 42, No. 10 (Oct., 1991), pp. 914-918
  25. ^ Dyer, J. S. (1990): Remarks on the Analytic Hierarchy Process. In: Management Science, 36 (3), S. 249
  26. ^ R. D. Holder "Response to Holder's Comments on the Analytic Hierarchy Process: Response to the Response" The Journal of the Operational Research Society, Vol. 42, No. 10 (Oct., 1991), pp. 914-918
  27. ^ MARI A. PÖYHÖNEN, RAIMO P. HÄMÄLÄINEN, AHTI A. SALO "An Experiment on the Numerical Modelling of Verbal Ratio Statements" Journal of Multi-Criteria Decision Analysis,vol 6, no 1, ppg 1-10, 1997
  28. ^ Stan Schenkerman "Inducement of nonexistent order by the analytic hierarchy process", Decision Sciences, Spring 1997
  29. ^ de Steiguer, J.E. (October, 2003), "The Analytic Hierarchy Process as a Means for Integrated Watershed Management" (PDF), in Renard, Kenneth G. (ed.), First Interagency Conference on Research on the Watersheds, Benson, Arizona: U.S. Department of Agriculture, Agricultural Research Service, pp. 736–740 {{citation}}: Check date values in: |date= (help); Unknown parameter |coauthors= ignored (|author= suggested) (help); Unknown parameter |coeditors= ignored (help)
Retrieved from "https://en.wikipedia.org/enwiki/w/index.php?title=Analytic_hierarchy_process&oldid=191566770"