Adaptive Huffman coding
Adaptive Huffman coding (also called Dynamic Huffman coding) is an adaptive coding technique based on Huffman coding. It permits building the code as the symbols are being transmitted, having no initial knowledge of source distribution, that allows one-pass encoding and adaptation to changing conditions in data.
The benefit of one-pass procedure is that the source can be encoded in real time, though it becomes more sensitive to transmission errors, since just a single loss ruins the whole code.
Algorithms
There are a number of implementations of this method, the most notable are FGK (Faller-Gallager-Knuth) and Vitter algorithm.
Vitter algorithm
Code is represented as a tree structure in which every node has a corresponding weight and a unique number.
Numbers go down, and from right to left.
Weights must satisfy the sibling property, that is what nodes can be listed in order of nonincreasing weight with each node adjacent to its sibling. Thus if A is parent node of B and node C is child of B, then .
The weight is merely the count of symbols transmitted which codes are associated with children of that node.
A set of nodes with same weights make a block.
To get the code for every node, in case of binary tree we could just traverse all the path from the root to the node, writing down (for example) "1" if we go to the right and "0" if we go to the left.
We need some general and straightforward method to transmit symbols which are not yet transmitted (NYT), we could use, for example, transmission of binary numbers for every symbol in alphabet.
Encoder and decoder start with only the root node, which has the maximum number. In the beginning it is our initial NYT node.
When we transmit an NYT symbol we have to transmit code for the NYT node, then for its generic code.
For every symbol which is already in the tree we only have to transmit code for its leaf node.
For every symbol transmitted on both sides we must execute update procedure:
- If current symbol is NYT, add two child nodes to NYT node, one will be a new NYT node the other is leaf node for our symbol, increase weight for new leaf node and old NYT, go to step 4, else go to symbol's leaf node.
- If this node does not have the highest number in a block swap it with which has the highest number
- Increase weight for current node
- If this is not the root node go to parent node, go to step 2, else end.
Note: swapping nodes means swapping weights and corresponding symbols, but not the numbers.
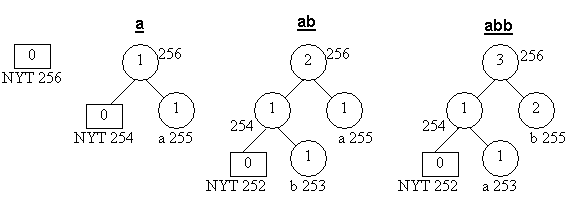
Example
Start with empty tree.
For "a" transmit its binary code.
NYT spawns two child nodes 254 and 255.
Weight for root is now 1.
Now code for "a", associated with node 255 is 1.
For "b" transmit 0 for NYT node, then its binary code.
NYT spawns two child nodes 252 for NYT and 253 for leaf node.
Increase weights for 253 and 254 and root.
For second "b" transmit 01.
Go to its leaf node 253, we have a block of weights of 1 and the biggest number in the block is 255, so swap the nodes, increase weight, go to root, increase weight for root.
Future code for "b" is 1, and for "a" is now 01, which reflects their frequency.
External links
This article incorporates public domain material from Paul E. Black. "adaptive Huffman coding". Dictionary of Algorithms and Data Structures. NIST.- University of California Dan Hirschberg site
- Cardiff University Dr. David Marshall site
- C implementation of Vitter algorithm