Butterfly diagram

Data-flow diagram connecting the inputs x (left) to the outputs y that depend on them (right) for a "butterfly" step of a radix-2 Cooley-Tukey FFT. This diagram resembles a butterfly (as in the Morpho butterfly shown for comparison), hence the name.

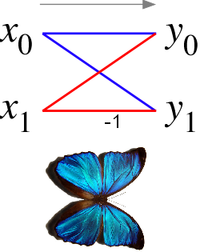
In the context of fast Fourier transform algorithms, a butterfly is a portion of the computation that combines the results of smaller discrete Fourier transforms (DFTs) into a larger DFT, or vice versa (breaking a larger DFT up into subtransforms). The name "butterfly" comes from the shape of the data-flow diagram in the radix-2 case, as described below. The same structure can also be found in the Viterbi algorithm, used for finding the most likely sequence of hidden states.

Most commonly, the term "butterfly" appears in the context of the Cooley-Tukey FFT algorithm, which recursively breaks down a DFT of composite size $n=rm$ into $r$ smaller transforms of size $m$ where $r$ is the "radix" of the transform. These smaller DFTs are then combined with a size-$r$ butterflies, which themselves are DFTs of size $r$ (performed $m$ times on corresponding outputs of the sub-transforms) pre-multiplied by roots of unity (known as twiddle factors). (This is the "decimation in time" case; one can also perform the steps in reverse, known as "decimation in frequency", where the butterflies come first and are post-multiplied by twiddle factors. See also the Cooley-Tukey FFT article.)

Radix-2 butterfly diagram

In the case of the radix-2 Cooley-Tukey algorithm, the butterfly is simply a DFT of size 2 that takes two inputs $(x_{0},x_{1})$ (corresponding outputs of the two sub-transforms) and gives two outputs $(y_{0},y_{1})$ by the formula (not including twiddle factors):

$y_{0}=x_{0}+x_{1}$

$y_{1}=x_{0}-x_{1}$

If one draws the data-flow diagram for this pair of operations, the $(x_{0},x_{1})$ to $(y_{0},y_{1})$ lines cross and resemble the wings of a butterfly, hence the name. (See also the illustration at right.)

More generally, a DFT on $n=2^{p}$ inputs with respect to a primitive $n$-th root of unity $\omega =\exp({\frac {2\pi i}{n}})$ relies on $O(n\log n)$ butterflies of the form:

$y_{0}=x_{0}+x_{1}\omega ^{i}$

$y_{1}=x_{0}-x_{1}\omega ^{i}$

Whereas the inverse transform with respect can mathematically be interpreted as a direct transform with respect to $\omega ^{-1}$, one may also directly invert the butterflies:

$x_{0}={\frac {1}{2}}(y_{0}+y_{1})$

$x_{1}={\frac {\omega ^{-i}}{2}}(y_{0}-y_{1})$

Recently, it was noticed by Joris van der Hoeven that the pair $(x_{0},y_{1})$ is also related to the pair $(x_{1},y_{0})$ by simple formulas:

$x_{0}=y_{0}-x_{1}\omega$

$y_{1}=y_{0}-2x_{1}\omega$

and

$x_{1}=(x_{0}-y_{1})\omega ^{-1}$

$y_{0}=2x_{0}-y_{1}$

These "flip"-relations are at the basis of a truncated version of the DFT.

External links

• explanation of the FFT and butterfly diagrams.
• butterfly diagrams of various FFT implementations (Radix-2, Radix-4, Split-Radix).