Beta distribution
|
Probability density function 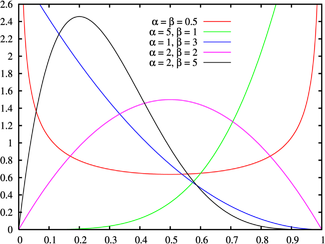 | |||
|
Cumulative distribution function 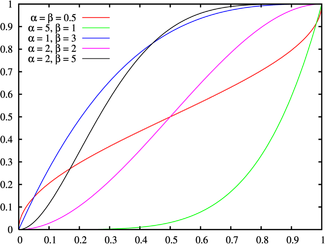 | |||
| Parameters |
shape (real) shape (real) | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Mean | |||
| Mode | for | ||
| Variance | |||
| Skewness | |||
| Excess kurtosis | see text | ||
| Entropy | see text | ||
| MGF | |||
| CF | |||
In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval [0, 1] parameterized by two positive shape parameters, typically denoted by α and β. It is the special case of the Dirichlet distribution with only two parameters. Since the Dirichlet distribution is the conjugate prior of the multinomial distribution, the beta distribution is the conjugate prior of the binomial distribution. In Bayesian statistics, it can be seen as the posterior distribution of parameter p of a binomial distribution after observing α -1 independent events with probability p and β -1 with probability 1-p.
Characterization
Probability density function
The probability density function of the beta distribution is:
where is the gamma function. The beta function, B, appears as a normalization constant to ensure that the total probability integrates to unity.
Cumulative distribution function
The cumulative distribution function is
where is the incomplete beta function and is the regularized incomplete beta function.
Properties
Moments
The expected value and variance of a beta random variable X with parameters α and β are given by the formulae:
The skewness is
The kurtosis excess is:
Quantities of information
Given two beta distributed random variables, X ~ Beta(α, β) and Y ~ Beta(α', β'), the information entropy of X is
where is the digamma function.
The cross entropy is
It follows that the Kullback-Leibler divergence between these two beta distributions is
Shapes
The beta density function can take on different shapes depending on the values of the two parameters:
- is U-shaped (red plot)
- or is strictly decreasing (blue plot)
- is the uniform [0,1] distribution
- or is strictly increasing (green plot)
- is strictly convex
- is a straight line
- is strictly concave
- is unimodal (purple & black plots)
Moreover, if then the density function is symmetric about 1/2 (red & purple plots).
Parameter estimation
Let
be the sample mean and
be the sample variance. The method-of-moments estimates of the parameters are
If the distribution is required over an interval other than [0, 1], say , then replace with and with in the above equations.[1][2]
Related distributions
- If X has a beta distribution, then T=X/(1-X) has a "beta distribution of the second kind", also called the beta prime distribution.
- The connection with the binomial distribution is mentioned below.
- The Beta(1,1) distribution is identical to the standard uniform distribution.
- If X and Y are independently distributed Gamma(α, θ) and Gamma(β, θ) respectively, then X / (X + Y) is distributed Beta(α,β).
- If X and Y are independently distributed Beta(α,β) and F(2β,2α) (Snedecor's F distribution with 2β and 2α degrees of freedom), then Pr(X ≤ α/(α+xβ)) = Pr(Y > x) for all x > 0.
- The beta distribution is a special case of the Dirichlet distribution for only two parameters.
- The Kumaraswamy distribution resembles the beta distribution.
- If has a uniform distribution, then or for the 4 parameter case, which is a special case of the Beta distribution called the power-function distribution.
- Binomial opinions in subjective logic are equivalent to Beta distributions.
Applications
B(i, j) with integer values of i and j is the distribution of the i-th order statistic (the i-th smallest value) of a sample of i + j − 1 independent random variables uniformly distributed between 0 and 1. The cumulative probability from 0 to x is thus the probability that the i-th smallest value is less than x, in other words, it is the probability that at least i of the random variables are less than x, a probability given by summing over the binomial distribution with its p parameter set to x. This shows the intimate connection between the beta distribution and the binomial distribution.
Beta distributions are used extensively in Bayesian statistics, since beta distributions provide a family of conjugate prior distributions for binomial (including Bernoulli) and geometric distributions. The beta(0,0) distribution is an improper prior and sometimes used to represent ignorance of parameter values.
The Beta distribution can be used to model events which are constrained to take place within an interval defined by a minimum and maximum value. For this reason, the Beta distribution—along with the triangular distribution—is used extensively in PERT, critical path method (CPM) and other project management / control systems to describe the time to completion of a task. In project management, shorthand computations are widely used to estimate the mean and standard deviation of the Beta distribution:
where a is the minimum, c is the maximum, and b is the most likely value.
These approximations are exact only for particular values of Alpha and Beta, specifically when[3]:
These are notably poor approximations for most other beta distributions exhibiting average errors of 40% in the mean and 549% in the variance[4][5][6]
References
- ^ Engineering Statistics Handbook
- ^ Brighton Webs Ltd. Data & Analysis Services for Industry & Education
- ^ Grubbs, Frank E. (1962). Attempts to Validate Certain PERT Statistics or ‘Picking on PERT’. Operations Research 10(6), p. 912-915.
- ^ Keefer, Donald L. and Verdini, William A. (1993). Better Estimation of PERT Activity Time Parameters. Management Science 39(9), p. 1986-1091.
- ^ Keefer, Donald L. and Bodily, Samuel E. (1983). Three-point Approximations for Continuous Random variables. Management Science 29(5), p. 595-609.
- ^ http://www.nps.edu/drmi/docs/1apr05-newsletter.pdf
External links
- Weisstein, Eric W. "Beta Distribution". MathWorld.
- "Beta Distribution" by Fiona Maclachlan, The Wolfram Demonstrations Project, 2007.
- Beta Distribution - Overview and Example, xycoon.com
- Beta Distribution, brighton-webs.co.uk



![{\displaystyle x\in [0;1]\!}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/394f69db847ba283727b0bc73bccc019572a72ae)









































![{\displaystyle \scriptstyle [\ell ,h]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/bcc4e5aba23f2120854fa2229d97dba92c7ca2c4)




![{\displaystyle X\sim {\rm {U}}(0,1]\,}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/de74bb323a07dccdd103dfd537ce9f9b85d0d5ce)




