Talk:Linear regression

Mergers?

The front page of this article tells me that someone has suggested it be merged with Multiple regression. I agree that it should be. Also, there are articles on

• Regression analysis
• Linear model
• Analysis of variance
• Analysis of covariance
• Robust regression

could also be merged in.

Please add to the above list if there are others.

Personally, I'd prefer "Linear model" as the title.

Since this is a subject on which a great many books have been written, an article on it is not going to be anything like comprehensive. It might therefore be sensible to lay down some rules on the content, such as the level of mathematical and theoretical rigour.

Perhaps someone should start a Wikibook to cover the gaps...

—The preceding unsigned comment was added by Tolstoy the Cat (talk • contribs) .

Regression analysis is about a far broader topic than linear regression. Obviously a merger, if any, should go in the other direction. But I would oppose any such merger. Obviously, many sorts of regression are neither linear models nor generalized linear models, so "linear model" would not be an appropriate title. Also, an analysis of variance can accompany any of various different sorts of regression models, but that doesn't mean analysis of variance should not be a separate article. Michael Hardy 00:23, 5 June 2006 (UTC)

PS: Could you sign your comment so that we know who wrote it without doing tedious detective work with the edit history? Michael Hardy 00:24, 5 June 2006 (UTC)

I would also prefer not to merge. There is a lot of good content here which would only be overwhelming detail for most readers of the more general Regression analysis article. -- Avenue 03:18, 6 June 2006 (UTC)

Shouldn't merge those. If anything, the entry on linear models should be expanded. That entry, by the way, has the confusing line 'Ordinary linear regression is a very closely related topic,' which is technically correct but implies that linear regression is somehow more related to linear models than ANOVA or ANCOVA. It's important to keep in mind the difference between linear modeling and linear regression. Linear models follow Y = X*B+E, where Y and E and B are vectors and X is a design matrix. Linear regression models follow Y = X*m+b, where Y and X are data vectors and m and b are scalars. I think the superficial similarity between those two formulas creates the impression that linear regression and linear modeling somehow share a special connection, beyond linear regression just being a special case, as is AN(C)OVA. So I'm going to change that line :-) -- —The preceding unsigned comment was added by 134.58.253.130 (talk • contribs).

Edits in 2004

In reference to recent edits which change stuff like <math>x_i</math> to ''x''_''i'' -- the math-tag processor is smart enough to use html markup in simple cases (instead of generating an image via latex). It seems that some of those changes weren't all that helpful, as the displayed text is unchanged and the html markup is harder to edit. I agree the in-line <math>x_1,\ldots,x_n</math> wasn't pretty; however, it does seem necessary to clarify "variables" for the benefit of readers who won't immediately see x as a vector. Wile E. Heresiarch 16:41, 2 Feb 2004 (UTC)

In reference to my recent edit on the paragraph containing the eqn y = a + b x + c^2 + e, I moved the discussion of that eqn up into the section titled "Statement of the linear regression model" since it has to do with the characterizing the class of models which are called "linear regression" models. I don't think it could be readily found in the middle of the discussion about parameter estimation. Wile E. Heresiarch 00:43, 10 Feb 2004 (UTC)

I have a question about the stronger set of assumptions (independent, normally distributed, equal variance, mean zero). What can be proven from these that can't be proven from assuming uncorrelated, equal variance, mean zero? Presumably there is some result stronger than the Gauss-Markov theorem. Wile E. Heresiarch 02:42, 10 Feb 2004 (UTC)

At least a partial answer is that the validity of such things as the confidence interval for the slope of the regression line, unsing a t-distribution, relies on the normality assumptions. More later, maybe ... Michael Hardy 19:51, 10 Feb 2004 (UTC)

It occurs to me that if independent, Gaussian, equal variance errors are assumed, a stronger result is that the least-squares estimates are the maximum likelihood estimates -- right? Happy editing, Wile E. Heresiarch 14:57, 29 Mar 2004 (UTC)

I think this is better illustrated by an example. Imagine that x are the numbers from 1 to 100, our model is y = 2 x - 1 + error (or something equally simple), but our error, instead of being a nice normal distribution, is the variable that has 90% chance of being a N(0,1) and 10% chance of being 1000 x N(0,1). It's intuitively obvious that doing the least square fit over this will usually give a wrong analysis, while a method that seeks and destroys the outliers before the lsf would be better.Albmont 14:09, 23 November 2006 (UTC)

Galton

Hello. In taking a closer look at Galton's 1885 paper, I see that he used a variety of terms -- "mean filial regression towards mediocrity", "regression", "regression towards mediocrity" (p 1207), "law of regression", "filial regression" (p 1209), "average regression of the offspring", "filial regression" (p 1210), "ratio of regression", "tend to regress" and "tendency to regress", "mean regression", "regression" (p 1212) -- although not exactly "regression to the mean". So it seems that the claim that Galton specifically used the term "regression to the mean" should be substantiated. -- Also this same paper shows that Galton was aware that regression works the other way too (parents are less exceptional than their children). I'll probably tinker with the history section in a day or two. Happy editing, Wile E. Heresiarch 06:00, 27 Mar 2004 (UTC)

Beta

I am confused -- i don't like the notation of d being the solution vector -- how about using Beta1 and Beta0?

Scientific applications of regression

The treatment is excellent but largely theoretical. It would be helpful to include additional material describing how regression is actually used by scientists. The following paragraph is a draft or outline of an introduction to this aspect of linear regression. (Needs work.)

Linear regression is widely used in biological and behavioral sciences to describe relationships between variables. It ranks as one of the most important tools used in these disciplines. For example, early evidence relating cigarette smoking to mortality came from studies employing regression. Researchers usually include several variables in their regression analysis in an effort to remove factors that might produce spurious correlations. For the cigarette smoking example, researchers might include socio-economic status in addition to smoking to insure that any observed effect of smoking on mortality is not due to some effect of education or income. However, it is never possible to include all possible confounding variables in a study employing regression. For the smoking example, a hypothetical gene might increase mortality and also cause people to smoke more. For this reason, randomized experiments are considered to be more trustworthy than a regression analysis.

I also don't see any treatment of statistical probability testing with regression. Scientific researchers commonly test the statistical significance of the observed regression and place considerable emphasis on p values associated with r-squared and the coefficients of the equation. It would be nice to see a practical discussion of how one does this and how to interpret the results of such an analysis. --anon

I will add it in. Please feel free to improve on it. Oleg Alexandrov 16:46, 6 August 2005 (UTC)

Use of Terms Independent and Dependent

I changed the terms independent / dependent variable to explanatory / response variable. This was to make the article more in line with the terminology used by the majority of statistics textbooks, and because independent / dependent variables are not statistically independent. Predictor / response might be ideal terminology, I'll see what textbooks are using.--Theblackgecko 23:06, 11 April 2006 (UTC)

The terms independent and dependent are actually more precise in describing linear regression as such - terms like predictor/response or explanatory/response are related to the application of regression to different problems. Try checking a non-applied stats book.

Scientists tend to speak of independent/dependent variables, but statistics texts (such as mine) prefer explanatory/response. (These two pairs are not strictly interchangeable, in any event, though usually they are.) Here is a table a professor wrote up for the terms: http://www.tufts.edu/~gdallal/slr.htm.

Merge?

At a broad and simplistic level, we can say that Linear Regression is generally used to estimate or project, often from a sample to a population. It is an estimating technique. Multiple Regression is often used as a measure of the proportion of variability explained by the Linear Regression.

Multiple Regression can be used in an entirely different scenario. For example when the data collected is a census rather than a sample, and Linear Regression is not necessary for estimating. In this case, Multiple Regression can be used to develop a measure of the proportionate contribution of independent variables.

Consequently, I would propose that merging Multiple Regression into the discussion of Linear Regression would bury it in an inappropriate and in the case of the example given, an relatively unrelated topic.

--69.119.103.162 20:42, 5 August 2006 (UTC)A. McCready Aug. 5, 2006

Multiple regression (or more accurately, multiple linear regression), is just the general case of linear regression. Most of the article deals with simple linear regression, which is a special case of linear regression. I think the section on multiple regression in this article suffices. I'm going to go ahead and merge the two. --JRavn ^talk 13:54, 31 August 2006 (UTC)

As the discussion on merging Trend line into this article did not go anywhere, I propose we delete the warning template from both pages. Classical geographer 16:50, 19 February 2007 (UTC)

I still think it should be merged. — Chris53516 ^(Talk) 17:01, 19 February 2007 (UTC)

Tools?

Would it be within the scope of Wikipedia to mention or reference how to do linear regressions in Excel and scientific / financial calculators? I think it would be very helpful because that's how 99% of people will actually do a linear regression - no one cares about the stupid math to get to the coefficients and the R squared.

In Excel, there is the scatter plot for single variable linear regressions, and the linear regression data analysis and the linest() family of functions for multi-variable linear regressions.

I believe the hp 12c only supports single variable linear regressions. —The preceding unsigned comment was added by 12.196.4.146 (talk • contribs) 15:21, 15 August 2006 (UTC)

It would be useful, but I don't think it should be included in a wikipedia article. Tutorials and how-tos are generally not considered encyclopedic. An external link to an excel tutorial should be ok though. --JRavn ^talk 22:12, 18 August 2006 (UTC)

It would not be useful to suggest using Excel; it would be dangerous. Excel is notoriously bad at many statistical tasks, including regression. A readable summary is online here. Try searching for something like excel statistical errors to read more. -- Avenue 11:35, 19 August 2006 (UTC)

Someone new to the topic who has quick access to a ubiquitous program like Excel could quickly fire it up and try out some simple linear regression first hand. I don't think an external link amounts to a suggestion as to the best tool. We should be trying to accommodate people unfamiliar with the topic, not people trying to figure out what's the best linear regression tool (that would be an article in itself). --JRavn ^talk 03:37, 22 August 2006 (UTC)

Useful comments to accomodate a wider audience

I am not a mathematician, but a scientist. I am most familiar with the use of linear regression to calculate a best fit y=mx + b to suit a particular set of ordered pairs of data that are likely to be in a linear relationship. I was wondering if a much simpler explanation of how to calculate this without use of a calculator or knowing matrix notation might be fit into the article somewhere. The texts at my level of full mathematical understanding merely instruct the student to plug in the coordinates or other information into a graphing calculator, giving a 'black box' sort of feel to the discussion. I would suspect many others who would consult wikipedia about this sort of calculation would not the same audience that the discussion in this entry seems to address, enlightening though it may be. I am not suggesting that the whole article be 'dumbed down' for us feeble non-mathematicians, but merely include a simplified explanation for the modern student wishing a slightly better explanation than "pick up your calculator and press these buttons", as is currently provided in many popular college math texts.The24frans 16:21, 18 September 2006 (UTC)frannie

I agree that this would be helpful. Although I have used this in my graduate coursework, I want to use the same for analysis on the job. Having a simplified explanation as the prior user suggests would be helpful, especially in my trying to explain the theory to my non-analytical staff. 216.114.84.68 20:23, 3 October 2006 (UTC)dofl

This article is next to useless to a person who was told that a certain result came from a linear regression analysis, and wanted to get a handle on what that means, which is areasonable use for an encyclopedia. Suggest someone come up with a lead paragraph aimed at the layperson, and focussing on the kind of analytical questions that can be addressed using this method. 64.219.131.215 (talk) 20:01, 21 February 2009 (UTC)

Independent and dependent variables

Why are these labeled as "technically incorrect"? There is no explanation or citation given for this reasoning. The terms describe the relationship between the two variables. One is independent because it determines the the other. Thus the second term is dependent on the first. Linear regressions have independent variables, and it is not incorrect to describe them as such. If one is examining say, the amount of time spent on homework and its effect on GPA, then the hypothetical equation would be:

GPA = m * (homework time) + b

where homework time is the independent variable (independent from GPA), and GPA is dependent (on homework time, as shown in the equation). I will remove the references to these terms as technically incorrect unless someone can refute my reasoning. -- Chris53516 21:06, 3 October 2006 (UTC)

--->I added the terms, and I also added the note that they are technically incorrect. They are technically incorrect because they are considered to imply causation. (unsigned comment by 72.87.187.241)

Endogenous/exogenous

The uses of "endogenous" and "exogenous" variables here are not consistent with the only way I've ever heard them used. Exogenous means outside of the model -- i.e., a latent/hidden variable. Endogenous describes a variable that IS accounted for by your model, be it independent OR dependent. See Wiki entry for "exogenous," which supports this.

I recommend that these two words be deleted from the list of alternate names for predictor and criterion variables. (unsigned comments by 72.87.187.241)

I have found economists use exogenous in lenear models to mean non response variables. The contrast is endogenous variables that appear on the right hand side of one or more other variables equations but also on the left hand side of their own regression. Pdbailey 00:06, 7 October 2006 (UTC)

Forecasting

I ran into linear regression for the purpose of forecasting. I believe this is done reasonably often for business planning however I suspect it is statistically incorrect to extend the model outside of its original range for the independent variables. Not that I am by any means a statistician. Worthly of a mention? -K

If you're going to use a statistical model for forecasting you inevitably will have to use it outside the data used to fit it. That's not the main issue. One issue is that people sometimes plug time series data into a regression model and use it to produce a forecast, along with a confidence interval for the forecast. The problem is that in a time series the error terms are usually correlated, which is a violation of the regression model assumptions. The effect is that series standard deviation is underestimated and the confidence intervals are too small. The model coefficients are also estimated inefficiently, but they are not biased. For business planning it is common to first remove the seasonal pattern and then fit a regression line to obtain the trend. All that is fine. More sophisticated time series methods use regression ideas, but use them in a way that correctly accounts for the serial correlaton in the error terms, so that confidence intervals for the forecasts can be produced. Yes, I do think it's worth a mention. Blaise 09:08, 11 October 2006 (UTC)

If you want to have a precise forecast (meaning that you get the prediction and the error), it's necessary to know the a posteriori distributions of the coefficients (inclination, intercept and standard deviation of the errors); see below for Uncertanties. Albmont 13:58, 23 November 2006 (UTC)

Regression Problem

I have the problem to combine some indicators using a weighted sum. All weights have to be located in the range from 0 till 1. And the weights should add to one.

The probability distribution is rather irregular therefore the application of the EM-algorithm would be rather difficult.

Therefore I am thinking about using a linear regression with Lagrange condition that all indicators sum to one.

One problem which can emerge consists in the fact that a weight derived by linear regression might be negative. I have the idea to filter out indicators with negative weights and redo the linear regression with the remaining indicators until all weights are positive.

Is this sensible or does someone knows a better solution. Or is it better to use neural networks? (unsigned comments of Nulli)

I would do this using a Bayesian regression. The irregular distribution could be approximated by a mixture. You can define the parameters in such a way that they sum to one. You can enforce the non-negativity simply by choosing priors that are positive only, e.g. lognormal or gamma. The (free) WinBUGS package would be suitable for doing the calculations.Blaise (talk) 13:25, 28 August 2008 (UTC)

Uncertainties

The page gives useful formulae for estimating alpha and beta, but it does not give equations for the level of uncertainty in each (standard error, I think). For you mathematicians out there, I'd love it if this were available on wikipedia so I don't have to hunt through books. 99of9 00:11, 26 October 2006 (UTC)

I got these formulas from many sources (some of which were wrong, but it was possible to correct doing a lot of test cases); for a regression y = m x + c + sigma N(0,1), we have that (mbar - m) * sqrt(n-2) * sigma(x) / s is distributed as a t-Student with (n-2) degrees of freedom, and n * s^2 / sigma^2 as a Chi-Square with (n-2) degrees of freedom, where

sigma(x)^2 is (sum(x^2) - sum(x)^2/n)/n

s^2 is (sum(y^2) - cbar sum(y) - mbar sum(xy))/n

however, I could not find a distribution for cbar. The test cases suggest that mbar and s are independent, cbar and s are also independent, but mbar and cbar are highly negatively correlated (something like -sqrt(3)/4) - but this may be a quirk of the test case. I would also appreaciate if the exact formulas were given. Albmont 13:52, 23 November 2006 (UTC)

I think I got those numbers now, after some deductions and a lot of simulations. The above formulas for the distribution of mbar and s are right; the distribution for cbar is weird, because there's no decent way to estimate it. OTOH, if we take c1 (for lack of a better name) = cbar + mbar xbar, then the variable (c1 - (m xbar + c)) * sqrt(n-2) / s is distributed as a t-Student with (n-2) degrees of freedom, and the threesome (mbar, c1, s) will be independent.Albmont 16:30, 23 November 2006 (UTC)

Polynomial regression

Would it be worth mentioning in this article that the linear regression is simply a special case of a polynomial fit? Below I copy part of the article rephrased to the more general case:

By recognizing that the regression model $y_{i}=\alpha _{0}+\alpha _{1}x_{i}+\alpha _{2}x_{i}^{2}\dots +\alpha _{m}x_{i}^{m}+\varepsilon _{i}$ is a system of polynomial equations of order m we can express the model using data matrix X, target vector Y and parameter vector $\delta$. The ith row of X and Y will contain the x and y value for the ith data sample. Then the model can be written as

${\begin{bmatrix}y_{1}\\y_{2}\\\vdots \\y_{n}\end{bmatrix}}={\begin{bmatrix}1&x_{1}&x_{1}^{2}&\dots &x_{1}^{m}\\1&x_{2}&x_{2}^{2}&\dots &x_{2}^{m}\\\vdots &\vdots &\vdots &&\vdots \\1&x_{n}&x_{n}^{2}&\dots &x_{n}^{m}\end{bmatrix}}{\begin{bmatrix}\alpha _{0}\\\alpha _{1}\\\alpha _{2}\\\vdots \\\alpha _{m}\end{bmatrix}}+{\begin{bmatrix}\varepsilon _{1}\\\varepsilon _{2}\\\vdots \\\varepsilon _{n}\end{bmatrix}}$

I recall using this in the past and it worked quite well for fitting polynomials to data. Simply zero out the epsilons and solve for the alpha coefficients, and you have a nice polynomial. It works as long as m<n. For the linear regression, of course, m=1. -Amatulic 18:57, 30 October 2006 (UTC)

Currently the article concludes with some material on multiple linear regression, which is actually more general than polynomial regression. However, noting polynomial regression there as perhaps an example would seem appropriate. Baccyak4H 19:20, 30 October 2006 (UTC)

Multiple linear regression is more general in the sense that it extends the basic linear regression to more variables; however, the equations are still first-order, and the section on multiple regressions isn't clear that (or how) it can be applied to polynomials. It isn't immediately obvious to me that the matrix expression in that section, when substituting powers of x for the other variables, is equivalent to the expression I wrote above.

the issue of being first order is really a semantic one; if you define the "Y" to be "X^2", it can be seen to be first order too. In fact, as you note below, in some sense it has to be first order to be considered linear regression. You're right about the ambiguity between your polynomial formulation and the current normal equations one. However, they should be fundamentally equivalent. That is why I suggested using the polynomial example here. Baccyak4H 19:57, 30 October 2006 (UTC)

What I suggested above is a replacement for the start of the Parameter Estimation section, presenting a more general case with polynomials and mentioning that solving the coefficients of a line is a specific case where m=1. I'm probably committing an error in calling it a "polynomial regression"; it's still a linear regression because the system of equations to be solved are linear equations.

Either there or at the end would be appropriate, I think. -Amatulic 19:43, 30 October 2006 (UTC)

Currently most of the article is about the y=mx+b case, what my edits referred to as "simple linear regression", and the section at the end generalizes. I notice there is a part in the estimation section that uses the matrix formulation of the problem which would be valid in the general case. Perhaps that could be moved into the multiple section as well as your content? Baccyak4H 19:57, 30 October 2006 (UTC)

Why does the section on polynomial regression not mention the Vandermonde matrix and use the V notation in place of X? This is how I have seen it. This is what the matrix is called in the documentation for solvers like Mathematica, MatLab, Octave, and others.

I am not a real mathematician—just a mechanical engineer. I had to use this technique in Excel because the equations from trend lines in Excel charts don't show enough precision. Jebix 23:41, 30 July 2007 (UTC)

There are several ways to do regression in Excel. If you use the LINEST function in Excel you can show the results to any precision. Similary if you use the Data Analysis ToolPak or the Solver. Blaise (talk) 13:24, 28 August 2008 (UTC)

Part on multiple regression

This section should be rewriten as it is not general: polynomial regression is only a special case of multiple regression. And there is no formula for correlation coefficient, which, in case of multiple regression, is called coefficient of determination. Any comments?

TomyDuby 19:29, 2 January 2007 (UTC)

The section on Multiple Regression already does describe the general case. Polynomial fitting is a subsection under that, and the text in that subsection correctly describes polynomial fitting as a special case of multiple regression. I'm not seeing the problem you perceive. -Amatulic 21:29, 2 January 2007 (UTC)

I accept your comment. But I would like to see the comment I made above about the correlation coefficient fixed. TomyDuby 21:24, 10 January 2007 (UTC)

I didn't address your correlation coefficient comment because I assumed you would just go ahead and make the change to the article. I just made a slight change pointing to the coefficient of determination article, but I didn't add a formula. Instead I added a link to the main article. -Amatulic 23:15, 10 January 2007 (UTC)

Thanks! I made one more change. I consider the issue closed. TomyDuby 13:34, 11 January 2007 (UTC)

Major Rewrite

The French version of this article seems to be better written and more organised. If there are no objections, I intend on translating that article into English and incorporating it into this article in the next month or so. Another point: all the article on regression tend to be poorly written, repeatative, and not clear on the terminology including linear regression, least squares and its many derivatives, multiple linear regression... Woollymammoth 00:08, 21 January 2007 (UTC)

I disagree with you analysis. Please DO NOT replace this page with a translation. If this page needs to be improved, improve it on its own. Wikipedia is not a source for translations of other webpages, even other Wikipedia pages. — Chris53516 ^(Talk) 14:51, 23 January 2007 (UTC)

2nd opinion: I disagree with both of you. Foreign articles can contain valuable content that enhances articles in English. I suggest to Woollymammoth that you create a sub-page off your userpage or your talk page, and put the translated article there. Then post a wikilink to it here so we can review it. There may be a consensus to replace the whole existing article, or to use bits and pieces of your efforts to improve the existing article. -Amatulic 17:10, 23 January 2007 (UTC)

The French Wikipedia is just like the English Wikipedia - it's not an original source and should probably not be cited or used, IMO. — Chris53516 ^(Talk) 18:03, 23 January 2007 (UTC)

I never said it should be cited. At the extreme, I'd prefer an English translation of a foreign article over an English stub article on the same suject any day. That's my point: If an article has value in another language, it has value in English. That may not be the case here; I only suggested that Woollymammoth make the translation available for evaluation. -Amatulic 02:57, 24 January 2007 (UTC)

Regarding Line of Best Fit Song

I used {{redirect5|Line of best fit|the song "Line of Best Fit"|You Can Play These Songs with Chords}} for the disambiguation template. It appears to be the best one to use based on Wikipedia:Template messages/General. The album page show "Line of Best Fit" in 3 different sections, so linking to 1 section is pointless and misleading. — Chris53516 ^(Talk) 17:25, 30 January 2007 (UTC)

Dear Chris:Concerning your reverts of the above, please check the link again. I edited to take account of your concern. That is, the freshly edited link takes someone to the first mention of the song, which there mentions where the only other reference is to that song in the article. I would appreciate either your responding on the Talk page for Linear regression, or my Talk page, or meeting the concern I expressed in my Edit summary. My thx. Thomasmeeks 19:38, 30 January 2007 (UTC)

The link you posted was not to the first instance, but the second. Check the page again. I don't see the point in debating this. Why are you so concerned that this points to a particular place in the article? It isn't necessary to worry about the length of the disambiguation note, and having anything above the article is distracting anyway (but there's nowhere else to put it), so both of your concerns don't really matter. — Chris53516 ^(Talk) 19:42, 30 January 2007 (UTC)

Thx for response. Sorry about overlooking first mention (I did use Find but from later section). No debate there. The explanation for Redirect5 template is:

Top of articles about well known topics with a redirect which could also refer to another article. (emph. added)

The song is not the CD or the band, so no mention of either is necessary. Anyone trying to get to the song can get there with a briefer disambig. A disambig that is longer than necessary can be a distraction. It looks like spam. And that can be annoying to a lot of people. Thx. -- Thomasmeeks 21:45, 30 January 2007 (UTC)

Well, perhaps we could use the same text, just replace the link to the album with the name of the song. How about:

"Line of best fit" redirects here. For the song "Line of Best Fit", see [[You Can Play These Songs with Chords|Line of Best Fit]].

That sound okay? — Chris53516 ^(Talk) 23:04, 30 January 2007 (UTC)

Better than worst, but the first sentence is unnecessary (those who got there via "Line of best fit" know it & those who didn't don't care). The 2nd sentence repeats "Line of best fit" unnecesarily ("here" works just as well and is shorter), but "See" is good. Convergence(;). BW, Thomasmeeks 02:39, 31 January 2007 (UTC)

Dude! Instead of wasting my time, did you even check "line of best fit"?? It doesn't even redirect here!! — Chris53516 ^(Talk) 23:11, 30 January 2007 (UTC)

It used to redirect here, but was recently changed to trend line, which isn't as good a fit. I have restored line of best fit to redirect to this article. -Amatulic 00:10, 31 January 2007 (UTC)

Merge of trend line

There seemed to be no objections to merging trend line into this article, so I went ahead. Cleanup would still be useful. Jeremy Tobacman 01:00, 23 February 2007 (UTC)

Major Rewrite

I have performed a major rewrite removing most of the repeative and redundant information. A lot of the information has been, or soon will be moved to the article least squares, where it should belong. This article should, in my opinion, contain information about different types of linear regression. There seems to be at least 2, if not more, different types: least squares and robust regression. All the theoretical information about least squares should be in the article on least squares. -- Woollymammoth 02:03, 24 February 2007 (UTC)

Confidence interval for $\beta _{i}$

It's still not clear (to me) what's the meaning of this:

The $100(1-\alpha )\%$ confidence interval for the parameter, $\beta _{i}$, is computed as follows:

${{\hat {\beta }}_{i}\pm t_{{\frac {\alpha }{2}},m-n}{\hat {\sigma }}{\sqrt {(\mathbf {X} ^{T}\mathbf {X} )_{ii}^{-1}}}}$

where t follows the Student's t-distribution with $m-n$ degrees of freedom.

The problem is that I don't know what is ${(\mathbf {X} ^{T}\mathbf {X} )_{ii}^{-1}}\,$ - is it the inverse of the diagonal ii-th element of $\mathbf {X} ^{T}\mathbf {X}$? (now that I ask, it seems that it is...).

Could we say that ${\frac {\hat {\beta }}{{\hat {\sigma }}^{2}}}\,$ follows some Multivariate Student Distribution with parameters $\mu =0\,$ and $\Sigma =(\mathbf {X} ^{T}\mathbf {X} )^{-1}\,$? Or is there some other expression for the distribution of ${\hat {\beta }}$? Albmont 20:05, 6 March 2007 (UTC)

I am sure for the confusion. I should have defined that notatation. In fact, (A^TA)^-1_ii is the element located at the i^th row and column of the matrix. —The preceding unsigned comment was added by Woollymammoth (talk • contribs) 19:34, 13 March 2007 (UTC).

Slope/Intercept equations for linear regression

http://en.wikipedia.org/enwiki/w/index.php?title=Linear_regression&oldid=110403867

I know this is simple minded and hardly advance statistics, but when need the equations to conduct a linear fit for some data points I expected wikipedia to have and more specifically this page, but they have been removed. See this page for the last occurance. It would be nice if they could be worked back in. --vossman 17:41, 29 March 2007 (UTC)

Estimating beta (the slope)

We use the summary statistics above to calculate ${\widehat {\beta }}$, the estimate of β.

${\widehat {\beta }}={nS_{XY}-S_{X}S_{Y} \over nS_{XX}-S_{X}S_{X}}.\,$

Estimating alpha (the intercept)

We use the estimate of β and the other statistics to estimate α by:

${\widehat {\alpha }}={S_{Y}-{\widehat {\beta }}S_{X} \over n}.\,$

A consequence of this estimate is that the regression line will always pass through the "center" $({\bar {x}},{\bar {y}})=(S_{X}/n,S_{Y}/n)$.

It is currently found on the article on Least squares. However, these formulae are not commonly used except for manual calculation for the single variable case (which is important in many academic cases, for example, tests). The matrix formulation of the problem is more appropriate for computer applications. Another possibility would be to place the formulae in a section titled: "Manual calculations of the parameters for the single variable case". Woollymammoth 20:25, 3 May 2007 (UTC)

Inaccurate wording in the 2nd paragraph

One would think that such a basic article which has probably been seen by thousands of people and has been around for years would no longer contain careless imprecision in its explanation of the basic concept. OK, that's the rant. Here's the problem--the first sentence of the 2nd paragraph, which attempts to explain part of the fundamental concept is as follows:

This method is called "linear" because the relation of the response to the explanatory variables is assumed to be a linear function of the parameters.

The reference to "explanatory variables" is nowhere explained. One is expected to know what "explanatory variables" might be, yet they have not been defined, explained, or referenced before this. Instead, the prior paragraph mentions "dependent variables" and "independent variables" and "parameters". What are "explanatory" variables? For that matter, "response" has also not been defined. I'm assuming the sentence means something like:

This method is called "linear" because the relation of the dependent variable to the independent variables is assumed to be a linear function of the parameters.

I'm sure this is all obvious to the people who know what linear regression is, but then they don't really need this part of the article anyway.

-fastfilm198.81.125.18 16:37, 16 July 2007 (UTC)

Name: Regression? Or Linear Models, or Linear Statistical Models, etc.

There are substantial portions of the literature which have moved away from the use of the term "regression". The term "regression" is used for historical reasons but does not capture the meaning of what is actually going on.

Terms such as "Linear Models", "Linear Statistical Models" are becoming at least as widely used as "linear regression" in the literature, and their meaning is more descriptive of what is actually going on. I think we ought to consider renaming this article and have "Linear regression" forward to the new page. At the very least, we ought to discuss the issues regarding naming on this page. Cazort 19:24, 17 October 2007 (UTC)

Best way to include this graphic

How should I include this graphic... or, maybe it's a bad graphic. In that case, how could I improve it? Do we even need something like this? Cfbaf (talk) 00:07, 29 November 2007 (UTC)

Context for introduction

The current introduction is not that friendly to the lay person. Can the introduction not be structured like this? 1. Regression modelling is a group of statistical methods to describe the relationship between multiple risk factors and an outcome. 2. Linear regression is a type of regression model that is used when the outcome is a continuous variable (e.g., blood cholesterol level, or birth weight).

This explains what linear regression is commonly used for, and tells the reader briefly when it is used. The current introduction simply does not provide enough context for the lay reader. We could also add a section at the end for links to chapters describing other regression models. --Gak (talk) 01:53, 16 December 2007 (UTC)

Regression model

I would argue that the term "regession model" is currently broader than just "linear regression" and therefore regression model should not therefore redirect to this page. I instead propose a separate article on regression modelling that describes other types of model and when each type of model is selected and for what purpose:

1. linear regression: continuous outcome variables
2. logisitic regression: dichotomous outcomes
3. Cox proportional hazards: time-to-event outcome data
4. ...etc.

That would tie together the various articles under one coherent banner and would be much more useful to the lay reader. It would also be a place that the various terms could be defined (outcome, outcome variable, dependent variable, independent variable, predictor, risk factor, estimator, covariate, etc.) and then each of the separate articles would then adopt the terminology agreed in the regression model article. --Gak (talk) 02:09, 16 December 2007 (UTC)

Incorrect Formulation of R² ?

Shouldn't Pearson's Coefficient R² be ESS/TSS instead of SSR/TSS? See the Coefficient of Determination page. I think what has happened here is that the earlier definitions of ESS and SSR have been switched. Amberhabib (talk) 05:59, 16 January 2008 (UTC)

bivariate regression

Well, I understand the matrix-notation of multiple regression and also have implemented this. But today I just wanted to see the formula for bivariate regression and its coefficients. For the casual reader here we should have these formulae, too. In an encyclopedia the knowledge of matrix-analysis should not be a prerequisite to get a simple solution for a simple subcase of a general problem...

--Gotti 06:31, 30 January 2008 (UTC)

Bivariate regression is not a case of multiple regression. "Multiple" means having a more-than-1-dimensional predictor variable. "Multivariate" (and in particular "bivariate") means having a more-than-1-dimensional response variable. Michael Hardy (talk) 06:34, 30 January 2008 (UTC)

So I misused the term bi-variate. I meant 1-response-1-predictor variable (two variables involved)--Gotti 10:19, 16 February 2008 (UTC) —Preceding unsigned comment added by Druseltal2005 (talk • contribs)

Another major revision

Along with a major revision of regression analysis and articles concerned with least squares I have given this article a thorough going-over. Notation is now consistent across all the main articles in least squares and regression, making cross-referencing more convenient and reducing the amount of duplicated material to what I hope is the minimum necessary. There has been considerable rearrangement of material to give the article a more logical structure, but nothing significant has been removed. The example involving a cubic polynomial has been transferred here from regression analysis. Petergans (talk) 10:23, 22 February 2008 (UTC)

The article has become a bit less informative as a result. The article was barely accessible to laymen before; now it's worse, especially with that example of modeling the height of women.

What happened to the section on polynomial fitting, which is a linear regression generalized to polynomials of any order (including first order)? That is an important piece of information that was removed. -~Amatulić (talk) 18:21, 22 February 2008 (UTC)

I appreciate what you are saying. Let me make two points. Firstly the layman's presentation is in regression analysis, which I hope is now more informative than before. This article is more thorough and therefore more technical. A perennial problem in WP is how to pitch articles for all types of reader. I'm assuming, perhaps wrongly, that the general reader will pick up the link to regression analysis in the lead-in, expecting to find there an overview. Secondly, I transferred the modeling example from regression analysis because I thought it was too technical to be there. In consequence, the section on polynomials became repetitive. In any case, a more general treatment is available in linear least squares. Petergans (talk) 09:40, 23 February 2008 (UTC)

Example: heights and weights

I have a couple of problems with this example:

• It says "Intuitively, we can guess that if the women's proportions are constant and their density too, then the weight of the women may depend on the cube of their height" but then goes on to model y (weight) as a function of both x (height) and x³ without further comment.
• In any case, that's not intuitive to me at all. Women's (and men's) proportions aren't constant regardless of height. To a first approximation, weight goes up as the square of height. That's why body mass index is calculated as weight / (height)².
• On a much more minor point, the caption to the first figure in this section isn't clear. "A plot of the data set confirms this supposition" What supposition? Figure captions should, as far as possible, stand alone. Certainly don't assume the reader has read the text first. Many of us tend to look at the pictures first and the caption should encourage us to read the text. The caption in the second figure needs updating too to reflect the move from regression analysis to here.

Sorry to sound so critical. I do appreciate the work you've put in to overhauling these articles and they are important. This article got over 48 000 hits in January, more than one a minute. Regards and happy leap day, Qwfp (talk) 17:48, 29 February 2008 (UTC)

Thanks for these comments. In fact the text that you quote was left unaltered from previous versions. I only cleaned up the numerical part. You are perfectly correct in your criticisms. In fact I was unhappy with the model and have already done a spreadsheet calculation using a quadratic rather than a cubic. The fit is pretty much as good as with the cubic. I'll look at revising this bit, probably over the weekend.

While I have your attention, I have a question regarding WP in general. Would it be possible to make the EXCEL spreadsheet which I used to check the calculations available as a link in the article? Even better, could one call up the spreasheet directly from inside WP? I guess I'm thinking of an analogue to the image tag. Petergans (talk) 21:18, 29 February 2008 (UTC)

Err, I very much doubt the last option is possible. For one thing Excel is a commercial product not available to all readers, so I think it might get frowned upon. I'm probably not the best person to ask though as I've only been here a few months (keep that quiet!). Try the WP:Help desk? I guess you could make it an external link if you have a suitable website to upload it to (sorry can't help you there at the moment). I guess the open-source solution would be to make code available in something like GNU Octave, not that I've ever used it. That would be analogous to putting gnuplot code on image pages for graphs. But though there are a lot of things in wikipedia i'd like to be able to easily verify, this is a long way from the top of my list. Qwfp (talk) 22:39, 29 February 2008 (UTC)

I do have my own website Hyperquad, so I could put a spreadsheet there, but I'd rather not. I found GNUmeric, an open source spreadsheet, which might be incorporated into WP, adding a whole new dimension of interactivity, but this is very low priority for me too. Petergans (talk) 12:26, 1 March 2008 (UTC)

But back to the article: I'm very glad to hear you're planning to revise this example. Personally I'd be interested to see a quadratic model with and without an intercept, as the definition of body mass index corresponds to a model without an intercept – a visual comparison of the two might be nice. But then again it might be more detail than is wanted for an example in this context. I'll leave it to you. Qwfp (talk) 22:39, 29 February 2008 (UTC)

Revision is nearly ready. If you enable e-mail (my preferences tab on Qwfp) I will send you the spreadsheet too. You comments will be appreciated. Petergans (talk) 21:33, 1 March 2008 (UTC)

For clarification, the final calculation was for $y=\beta _{0}+\beta _{1}ht^{4}$. Petergans (talk) 23:24, 2 March 2008 (UTC)

Clarification on confidence intervals

The section on "Regression statistics" is a little unclear. Expressions for the "mean response confidence interval" and "predicted response confidence interval" are given, but the terms are not defined. They are also not defined or mentioned in the Error_propagation page. Can someone define what these terms mean? And also possibly give a more detailed derivation for where the expressions come from? --Jonny5cents2 (talk) 09:24, 10 March 2008 (UTC)

I agree. These expressions were carried over from previous versions. It needs a statistician to provide clarification. Petergans (talk) 11:10, 10 March 2008 (UTC)

Perhaps consider this: There are generally two predictions of interest having obtained the regression statistics. Suppose an experimenter could set $x=x_{d}$, but wants to predict the behaviour of $y_{d}$ instead of actually measuring $y_{d}$. There might be interest in estimating the mean of the population from which $y_{d}$ would be drawn, or instead there might be interest in predicting what value $y_{d}$ might be. The first of these is called the mean response, and the second of these is called the predicted response. The expectation value of both of these will be the same -- the value of $y_{d}$ is given by the substituted value of the regression line,$y_{i}=\sum _{j=1}^{j=n}X_{ij}{\hat {\beta _{j}}}$ evaluated at the point $x=x_{d}$. However the confidence intervals for the two differ.

Consider the mean response. That is, consider estimating the mean of the $y$ population associated with $x_{d}$, that is $E(y|x_{d})$. The variance one observes in the mean of the predicted value is ${\text{Var}}\left(\sum X_{ij}{\hat {\beta _{j}}}\right)$. In the linear case, $y=\alpha +\beta x$, the variance is given by ${\text{Var}}\left({\hat {\alpha }}+{\hat {\beta }}x_{d}\right)={\text{Var}}\left({\hat {\alpha }}\right)+\left({\text{Var}}{\hat {\beta }}\right)x_{d}^{2}+2x_{d}{\text{Cov}}\left({\hat {\alpha }}{\hat {\beta }}\right)$. For the linear case, this can be shown to be $\sigma ^{2}\left({\frac {1}{n}}+{\frac {\left(x_{d}-{\bar {x}}\right)^{2}}{\sum (x_{i}-{\bar {x}})^{2}}}\right)$

The predicted response is the expected range of values of $Y$ at some confidence level, $100(1-\alpha )\%$. The predicted response distribution is more easily calculated -- it is the predicted distribution of the residuals at some point $x_{d}$. So the variance is given by ${\text{Var}}\left(y_{d}-\left(\sum X_{ij}{\hat {\beta _{j}}}\right)\right)={\text{Var}}\left(y_{d}\right)+{\text{Var}}\left(\sum X_{ij}{\hat {\beta _{j}}}\right)$. The second part of this expression was already calculated for the mean response. In the linear case, this is ${\text{Var}}\left(y_{d}\right)+{\text{Var}}\left({\hat {\alpha }}+{\hat {\beta }}x_{d}\right)=\sigma ^{2}+\sigma ^{2}\left({\frac {1}{n}}+{\frac {\left(x_{d}-{\bar {x}}\right)^{2}}{\sum (x_{i}-{\bar {x}})^{2}}}\right)=\sigma ^{2}\left(1+{\frac {1}{n}}+{\frac {\left(x_{d}-{\bar {x}}\right)^{2}}{\sum (x_{i}-{\bar {x}})^{2}}}\right)$.

What do you guys thinks of this? Velocidex (talk) 04:00, 11 March 2008 (UTC)

Just what the doctor ordered! I suggest that this material be turned into a new article "Mean and predicted response" with redirects from "mean response" and "predicted response". It will need only a little editing and a brief intro, like "In regression analysis mean response ... I will be happy to do this if Velocidex will check what I write. Just two small questions remain:

1. is n the number of observations? If so it should be m for consistency.
2. the derivation of the variance formula is far from clear to me. The variance expression becomes

${\text{Var}}\left({\hat {\alpha }}+{\hat {\beta }}x_{d}\right)={\frac {\sigma ^{2}}{m\sum x_{i}^{2}-(\sum x_{i})^{2}}}\left(\sum x_{i}^{2}+mx_{d}^{2}-2x_{d}\sum x_{i}\right)$

Right? It's a big jump from there to the simplified formula.Petergans (talk) 08:50, 11 March 2008 (UTC)

Consider first the expression $\sum (x_{i}-{\bar {x}})^{2}$. This equals:

$\sum (x_{i}^{2}-2{\bar {x}}x_{i}+{\bar {x}}^{2})$

$=\sum x_{i}^{2}-2{\bar {x}}\sum x_{i}+\sum ({\bar {x}}^{2})$

Now make use of the fact that ${\bar {x}}={\frac {1}{m}}\sum (x_{i})\rightarrow \sum x_{i}=m{\bar {x}}$ to get

$=\sum x_{i}^{2}-2{\bar {x}}m{\bar {x}}+m{\bar {x}}^{2}$

$=\sum x_{i}^{2}-2m{\bar {x}}^{2}+m{\bar {x}}^{2}$

$=\sum x_{i}^{2}-m{\bar {x}}^{2}$

$=\sum x_{i}^{2}-m\left({\frac {1}{m}}\sum x_{i}\right)^{2}$

$\therefore \sum (x_{i}-{\bar {x}})^{2}=\sum x_{i}^{2}-{\frac {1}{m}}\left(\sum x_{i}\right)^{2}$

Now look at

${\frac {1}{m}}+{\frac {\left(x_{d}-{\bar {x}}\right)^{2}}{\sum (x_{i}-{\bar {x}})^{2}}}$.

$={\frac {\sum (x_{i}-{\bar {x}})^{2}+m(x_{d}-{\bar {x}})^{2}}{m\sum (x_{i}-{\bar {x}})^{2}}}$

The top line gives

$\sum x_{i}^{2}-{\frac {1}{m}}(\sum x_{i})^{2}+m\left[x_{d}^{2}-{\frac {2x_{d}}{m}}\sum x_{i}+{\frac {1}{m^{2}}}(\sum x_{i})^{2}\right]$

$=\sum x_{i}^{2}-{\frac {1}{m}}(\sum x_{i})^{2}+mx_{d}^{2}-2x_{d}\sum x_{i}+{\frac {1}{m}}(\sum x_{i})^{2}$

$=\sum x_{i}^{2}+mx_{d}^{2}-2x_{d}\sum x_{i}$

The bottom line gives $m\sum x_{i}^{2}-\left(\sum x_{i}\right)^{2}$ from the result before.

Therefore the total expression is

${\frac {\sum x_{i}^{2}+mx_{d}^{2}-2x_{d}\sum x_{i}}{m\sum x_{i}^{2}-\left(\sum x_{i}\right)^{2}}}$

Which is the hard part of the result you had before :) You can obviously go the other way, but its a little tricker knowing how to factorise things :) Velocidex (talk) 09:58, 11 March 2008 (UTC)

Problem with consistency of definition of vectors

Consider the lines:

Writing the elements $X_{dj},\ j=1,n$ as $\mathbf {z} ^{T}$, the $100(1-\alpha )\%$ mean response confidence interval for the prediction is given, using error propagation theory, by:

$\mathbf {z{\hat {\boldsymbol {\beta }}}} \pm t_{{\frac {\alpha }{2}},m-n}{\hat {\sigma }}{\sqrt {\mathbf {z(X^{T}X)^{-1}z^{T}} }}$

The multiplication $\mathbf {(X^{T}X)^{-1}z^{T}}$ does not make sense unless $\mathbf {z^{T}}$ is a column vector. i.e. the matrix $\mathbf {(X^{T}X)^{-1}}$ has n rows and n columns, therefore $\mathbf {z^{T}}$ must have n rows and 1 column. The standard definition of a vector within both physics and maths is that vectors are, by default, column vectors. Therefore $\mathbf {z}$ should be a column vector, not a row vector as is implied.

I propose that the entry should read $\mathbf {z^{T}(X^{T}X)^{-1}z}$. This gives the correct contraction to a scalar. Velocidex (talk) 03:21, 11 March 2008 (UTC)

Done! Petergans (talk) 09:02, 11 March 2008 (UTC)

Question on example

In the article it reads:

---

Thus, the normal equations are

${\begin{bmatrix}15&24.76&41.05\\24.76&41.05&68.37\\41.05&68.37&114.35\\\end{bmatrix}}{\begin{bmatrix}{\hat {\beta }}_{0}\\{\hat {\beta }}_{1}\\{\hat {\beta }}_{2}\\\end{bmatrix}}={\begin{bmatrix}931\\1548\\2586\\\end{bmatrix}}$

${\hat {\beta }}_{0}=129\pm 16$

${\hat {\beta }}_{1}=-143\pm 20$

${\hat {\beta }}_{2}=62\pm 6$

---

Where do the the +/- 16, 20 and 6 values come from?

62.92.124.145 (talk) 09:05, 12 March 2008 (UTC)

In the section Regression statistics

The standard deviation on a parameter estimator is given by
${\hat {\sigma }}_{j}={\sqrt {{\frac {S}{m-n}}\mathbf {(X^{T}X)} _{jj}^{-1}}}$

$\pm$ 16 means that the standard deviation is 16. Maybe that should be stated explicitly? The actual calculation by hand is laborious as it involves the inversion of a 3 by 3 matrix (see, for example, Adjugate matrix and Laplace expansion). I used an EXCEL spreadsheet to do it (function MINVERSE). Petergans (talk) 10:11, 12 March 2008 (UTC)

There is an explicit (and not so complicated) formula for the 3x3 matrix inversion from Cramer's rule, although I admit it is somewhat unwieldy.

You only need the main diagonal entries, however. You can make use of the fact that the matrix is symmetric. If you label the components of $\mathbf {X^{T}X}$ as $a_{ij}$, and call the inverse matrix components $C_{ij}$, then explicit formulae are given by:

$C_{00}={\frac {a_{11}a_{22}-a_{12}^{2}}{D}}$, $C_{11}={\frac {-a_{02}^{2}+a_{00}a_{22}}{D}}$ and $C_{22}={\frac {-a_{01}^{2}+a_{00}a_{11}}{D}}$, where $D$ is the determinant of the 3x3 matrix i.e. $D=2a_{02}a_{01}a_{12}-a_{02}^{2}a_{11}-a_{01}^{2}a_{22}+a_{00}a_{11}a_{22}-a_{00}a_{12}^{2}.$ Velocidex (talk) 10:46, 12 March 2008 (UTC)

OK, but these are diagonal elements only. The complete inverse requires the calculation of six 2 by 2 determinants. What I would really like to do is to post the spreadsheet file on a secure, public web site. I could use my own web site but that does not seem the right way to go about it. Petergans (talk) 14:51, 12 March 2008 (UTC)

Personally I'd prefer to avoid the use of ± for standard error altogether. It's often not clear whether it gives the standard error (i.e. standard deviation of the estimate), confidence interval, or (when used with a mean) the population standard deviation or range. I'd prefer 129 (SE 16), or 129 (16) in a table with a heading of "estimate (standard error)". I'm sure i've seen the same point made in some medical statistics textbook or article by a respected author but I can't put my finger on it just now. Qwfp (talk) 11:13, 12 March 2008 (UTC)

In cases where there is possible ambiguity it is always best to state explicitly the convention that has been used. The $\pm$ notation has the advantage of compactness, so I've amended the text accordingly. Petergans (talk) 14:51, 12 March 2008 (UTC)

The values here should be the confidence intervals. The factors from the inverse matrix give the standard errors, and the factor ${\sqrt {S/(m-n)}}$ corrects for $\chi _{\nu }^{2}\neq 1$ (where $\nu$ is the number of degrees of freedom $=m-n$). Check out chapter 15 (I think?) of Numerical Recipes for an explanation of the origin of this factor. Dropping the ${\sqrt {S/(m-n)}}$ term gives the formal standard errors. Velocidex (talk) 22:51, 13 March 2008 (UTC)

Using plus-or-minus the SD does not make sense; one should instead use confidence intervals that get smaller as the sample size grows, even if the SD stays the same. Michael Hardy (talk) 00:20, 14 March 2008 (UTC)

It is NOT plus or minus the SD; it is in fact plus or minus the confidence interval. As I said above, if you remove the factor ${\sqrt {S/(m-n)}}$, you will get the standard error. You can verify that the supplied values do in fact go to zero with infinite sample size. Consider, for instance, the formula for the mean response (which gives the effective confidence limits on the regression line). The factor 1/m goes to zero as $m\rightarrow \infty$. Similarly, the expression $\sum (x_{i}-{\bar {x}})^{2}$ goes to infinity as m goes to infinity for any distribution with non-zero variance (i.e. any distribution you will obtain in the real world). Therefore the term ${\frac {(x_{d}-{\bar {x}})^{2}}{\sum (x_{i}-{\bar {x}})^{2}}}$ will also go to zero as m goes to infinity. Thus the confidence interval on the regression line shrinks to zero size with an infinite number of measurements; this is exactly the property you describe. You can show the same thing occurs for the formulae given for the individual parameter estimates also. Velocidex (talk) 05:26, 14 March 2008 (UTC)

Once again it becomes apparent that there are completely different approaches within different disciplines. In my discipline, chemistry, it is customary to give standard deviations for least squares parameters. Confidence limits are only calculated when they are required for a statistical test. There is a good reason for this. To derive confidence limits an assumption has to be made concerning the probability distribution of the errors on the dependent variable, y. For example, the parameters will belong to a Student's t distribution if the distribution is Gaussian. The assumption of a Gaussian distribution may or may not be justified. In short, the results of the linear regression calculations are value and standard deviation, regardless of the error distribution function. Confidence limits are derived from those results with a further assumption.

Concerning the factor ${\sqrt {S/(m-n)}}$ this is an estimator of the error of an observation of unit weight. Another way to eliminate this factor is to estimate the error experimentally as $\sigma$ and do a weighted regression, minimizing $\sum r^{2}/\sigma ^{2}\,$. Petergans (talk) 09:45, 14 March 2008 (UTC)

I agree you have to make an assumption about the probability distribution to derive confidence limits, but the whole point of this article is that you are trying to fit a linear function where no variance estimate is available for each parameter. If it was, you would use a proper $\chi ^{2}$ minimisation (weighted least squares) -- and would have the benefit of an independent goodness-of-fit probability (assuming normal distribution of errors). If you DON'T think your errors are normal, then you shouldn't be using least squares anyway, because the least squares process starts out with the assumption that your errors are normally distributed... I agree with what you are saying, Petergans, but its beyond the scope of this article. perhaps worth commenting on, but if you really think your errors are significantly non-normal (and you have a handle on the underlying distribution) then you should maximise the explicit likelihood function.

Note that if you do use $\chi ^{2}$, you still have to multiple by ${\sqrt {\chi ^{2}}}$ to account for overdispersion (caused by variance understimation)Velocidex (talk) 11:54, 14 March 2008 (UTC)

Alternatively you can use bootstrap resampling to determine empirical confidence limits without any knowledge of the underlying distribution. Velocidex (talk) 07:07, 15 March 2008 (UTC)

It is a common misunderstanding to think that the least squares procedure can only be applied when the errors are normally distributed. The Gauss–Markov theorem (and Aitken extesion) is independent of the error distribution function. The misunderstanding arises because the Gauss's method is sometimes (e.g. Numerical Recipes) derived using the maximum likelihood principle; when the errors are normally distributed the maximum likelihood solution coincides with the minimum variance solution.

A simple example is the fitting of radioactive decay data. In that case the errors belong to a Poisson distribution but this does not mean that least squares cannot be used. Admittedly this is a nonlinear case, though for a single (exponential) decay it can be made into a linear one by a logarithmic transformation which also transforms the error distribution into I know not what. Other nonlinear to linear transformations have been extensively used in the past See non-linear least squares#Transformation to a linear model for more details. Even if the original data were normally distributed, the transformed data certainly would not be.

I have made the assumption of normality explicit in the example. Petergans (talk) 08:55, 15 March 2008 (UTC)

M vs. N

In the Definitions section right at the start the number of values is given as m, not n (which is surely more usual) "The data consist of m values y1,...,ym taken etc", then the first summation following has usage of n, which is not previously or nearby defined. It appears that the x-variable beta, is potentially an order-n vector and the simple case of (x,y) points would be with order n = 1. If this is so, words to this effect would be good, rather than exhibiting a tersely cryptic but high-formalism demonstration of superior knowledge in the minimum number of words. Regards, NickyMcLean (talk) 21:18, 23 April 2008 (UTC)

I have clarified the fact that there are n parameters in general. Petergans (talk) 09:07, 24 April 2008 (UTC)

This issue needs revisiting

I gather there has been some discussion of this notation. In which discipline(s) is it conventional to use "M" for the sample size and "N" for the number of covariates? This seems strange and confusing to me given that in, at least, statistics, econometrics, biostatistics, and psychometrics, "N" conventionally denotes the sample size. Common statistical jargon such as "root n consistency" even invokes that convention. I think it is non-standard and possibly very confusing to use "N" as it is used in this and other wiki articles. —Preceding unsigned comment added by 68.146.25.175 (talk) 16:48, 28 July 2008 (UTC)

I prefer lower-case n for the sample size and something else for the number of predictors. Michael Hardy (talk) 18:28, 28 July 2008 (UTC)

F-test and validity checking?

In the Article's section "Checking model validity" it is mentioned the method of F-test. Can anyone explain this further?

IMHO there are two issues that need clarification.

• How is the F-test related to linear regression? According to my understandings, the F-test is used to justify the tradeoff between the loss of degree-of-freedom and the gain of reduced residuals (well, this is far from being a mathematically rigorous description). To make use of F-test, we compare the linear model to be studied with another one, which differs from the former by a few DOF. This is essentially asking whether it is worth adding another component in the fitting. E.g. if we performed F-test against a straight-line model (null hypothesis) and a third-order polynomial one, and the null hypothesis was rejected, we say the 3rd-order polynomial one was "validated." Is that right?
• Is it true that the result of the F-test could be fully justified only when the errors of the dependent variable satisfy the Gaussian distribution with zero mean? I've heard that the F-test is somehow "fragile" about the Gaussianity of the errors.

I may be wrong. If you know about these issues please feel free to make them clear. Frigoris (talk) 16:58, 25 April 2008 (UTC)

Figure quality

This is not a most important issue, but if two figures in the section "Example" would be even better in SVG format. —Preceding unsigned comment added by Frigoris (talk • contribs) 17:04, 25 April 2008 (UTC)

Reversion of 29 April

NickyMcLean: please consider the following points.

1. There are probably as many authors who use n for the number of data points as there are those who use n for the number of parameters. The choice is arbitrary and neither is better than the other.

Yes, all naming noises are arbitrary choices though some are onomatopoeic in origin and so not purely arbitrary. However, some choices are better than others as they have mnemonic value that can be used to assist memory, a process universal in computer programming where the count of symbolic names is large. Thus, when one thing only is being counted, the choice of symbol for the count is very often N, or N-something or something-N or similar for the number of observations or whatever is being numbered. Here, there are two things to count. One of them is still the number of observations, and the other is a count of something to do with a "model". So as any fool can see, the choice must be M for the number of observations and N for the model, and this is to be done consistently since it is universally correct.NickyMcLean (talk) 05:18, 3 May 2008 (UTC)

1. The article has been recently under intensive development by a number of editors: all have accepted the choice of n for the number of parameters.

Or, were indifferent to n vs. m, or, found other details more interesting.NickyMcLean (talk) 05:18, 3 May 2008 (UTC)

1. See Talk:Least_squares#A major proposal for the context of this article in the general topic of least squares and regression analysis.

Yes, there could be a merger/reorganisation of least squares, polynomial, functional, multiple regression.NickyMcLean (talk) 05:18, 3 May 2008 (UTC)

1. The expression $y_{i}=\sum _{j=1}^{n}X_{ij}\beta _{j}+\varepsilon _{i}$ is correct. If you look at the example you will see that all $X_{i1}$ are equal to one. I think you are confusing the coefficient X with the independent variable x.

Yes, and the example is a long way away from the ill-phrased and vague "Definitions" section at the start, which is what set me off. See below.NickyMcLean (talk) 05:18, 3 May 2008 (UTC)

1. If you think something is seriously wrong, raise the issue on the talk page. Talk pages are watched by many experts in the topic and one of them will usually answer your query.

Petergans (talk) 08:11, 29 April 2008 (UTC)

... in addition, treating the "constant" term separately in the introductory material would make all the later stuff in the article incorrect, with the necessity to redefine everything in order for the matrix-based stuff to be presentable in simple form. Melcombe (talk) 14:27, 29 April 2008 (UTC)

Quite so, I approached the issue untidily to start with. I particularly objected to the sloppy phrase "The coefficients Xij are constants or functions of the independent variable" since in the absence of clear phrasing this could be read as arbitrary different constants being scattered at random throughout X and no particular structure to any function usage either. Yes, I know that everyone who already knows about this wouldn't be uncertain. The example (much later) makes the matter clear, but clarity should be attained by the definitions at the start being clear. Thus, after thinking through the details, I revised the definition so as to show the organisation of the columns of X (with no randomness possible), and which conformed to the usage "all in X" so that indeed the remainder of the article would be in order, with the definitions conforming to the usage and all the later matrix manipulation correct. I should have done this to start with. Likewise, I introduced the importance of no linear dependencies amongst the columns of X (including the constant column), but later revisions have ejected this and reintroduced the vagueness as to where constants and functions might appear in the organisation of X, though shortly (for the first order model) an implication is made. The conversion from $\beta _{0}\beta _{1}$ to $\beta _{1}\beta _{2}$ has however removed one unnecessary confusion.NickyMcLean (talk) 05:18, 3 May 2008 (UTC)

n must be the number of parameters for reasons of consistency with related articles in Wikipedia. Otherwise a reader who jumps from one article to another will be totally confused. Petergans (talk) 08:06, 2 May 2008 (UTC)

What are these well-organised related articles with which conformity would be wonderful? Precisely. The Regression_analysis article used M in some places and N in others, and in the Talk:Least_squares there is (shock, horror) usage of N as the Number of values, as is Normal. Need I quote textbooks that use N? I have earlier mentioned Wolfram mathworld which also uses NNickyMcLean (talk) 05:18, 3 May 2008 (UTC)

In a rare show of solidarity with Peter, I very much prefer that n be the number of variables, while m is the number of observations. That makes the Jacobian matrix at Gauss-Newton method and the matrix of the linear system at linear least squares to be m×n which is nicer than n×m.

I am not convinced by the fact that Mathworld uses m for number of variables. Oleg Alexandrov (talk) 06:09, 3 May 2008 (UTC)

Based on the first several references for linear least squares on Google books, that is, the links: [1], [2], [3], [4], [5], [6], I have seen n observations with p unknowns in one place, n observations with k unknowns in a different place, but m observations with n unknowns in four places, and nowhere have I seen n observations with m unknowns.

Anyway, I prefer m observations and n unknowns, for the reason stated earlier. Oleg Alexandrov (talk) 06:22, 3 May 2008 (UTC)

I've reverted User:Petergans again; although his choice of n and m may make more sense, the text does not make sense. Also, the note about the independent variables not being linearly dependent is important. — Arthur Rubin (talk) 18:06, 8 May 2008 (UTC)

Why I reverted Arthur Rubin's edits

I was surprised by Arthur Rubin's edit to linear regression with its edit summary that was so emphatic about PROPER explanation of linearity. I was concerned that some of your words might be misunderstood as meaning that polynomial regression is not an instance of linear regression, and then I came to your assertion that if one column of the design matrix X contains the logarithms of the corresponding entries of another column, that makes the regression nonlinear (presumably because the log function is nonlinear). That is grossly wrong and I reverted. Notice that the probability distributions of the least-squares estimators of the coefficients can be found simply by using the fact that they depend linearly on the vector of errors (at least if the error vector is multivariate normal). Nonlinearity of the dependence of one column of the matrix X upon the other columns does not change that at all, since the model attributes no randomness to the entries in X. Nonlinear regression, on the other hand, is quite a different thing from that. Michael Hardy (talk) 19:10, 8 May 2008 (UTC)

Why I reverted NickyMcLean's edits

While having some relevant points it was basically wrong. It is possible for both variables X and Y to be measured with error and to do regressions of both Y on X and X on Y and both will be valid provided it is recognised what is being done: to provide the best predictor of Y given values of X when they are measured with the same type of error as in the sample ... and this is a perfectly valid thing to do. Of course the requirement might be to try to identify an underlying relationship of "true" values, in which case the section on "errors in variables" is relevant. Melcombe (talk) 09:29, 23 May 2008 (UTC)

Well, gee whillikers. In my rejected text appears "...which should be the "predictor" and which the "predicted" variable? After some consideration,..." which does rather correspond to "both Y on X and X on Y" though obviously in different words and with a discussion of the issue. So just what is the "basically wrong"? Exactly? Are you scared by the usage of the notion "Deconstruction"?NickyMcLean (talk) 03:52, 24 May 2008 (UTC)

I must say I am also happy the ==Deconstruction== section is gone. It is lengthy and confusing, and I don't think it adds value to the article. Oleg Alexandrov (talk) 04:59, 24 May 2008 (UTC)

Alright, let's get this straight. In the example of actual use with actual data there is to be no discussion of:

• The accuracy and meaning of the measurements and how this might relate to how they are made,
• The choice of (height,weight) rather than (weight,height) even though the same theory would be used for either,
• That the original measurements have been grouped into height bands and the weights are averages for each group,
• How this grouping produces data that conforms to the statistical desiderata even if the source data do not,
• Possible confusions over the middle or edge value as being representative of each group's span,
• That the conversion to metric has been bungled with visible effects obvious to anyone who actually looks, but not in theory,
• The introduction of height and height² (I ran out of time to discuss that, but now, why bother?) for no apparent reason, and which, incidentally, would be affected by middle/edge confusions in grouping. Being non-linear, like.

Because talking about all these matters is too lengthy and anyway theory, brilliantly described with brief formulae, ought never be sullied with practice, lest theoreticians be confused and this is basically wrong. Examples are there solely to illumine the ignorant with the pure light of theory reflected thereby and actual practitioners are to genuflect and be awed. Those desiring to learn something are to gaze at and recite the cryptic formulae, and understanding will come. NickyMcLean (talk) 21:22, 25 May 2008 (UTC)

For reader convenience, here is my reconstitution of the plot of the residuals.

Converting the height values to inches and then correctly converting to metres produces a different quadric fit, with these (much smaller) residuals.

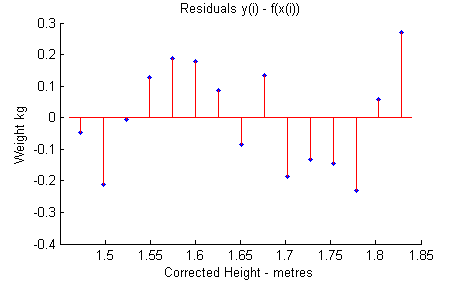
The resulting residuals suggest a cubic shape, so why not try fitting a cubic shape while I'm at it? These residuals are the result.

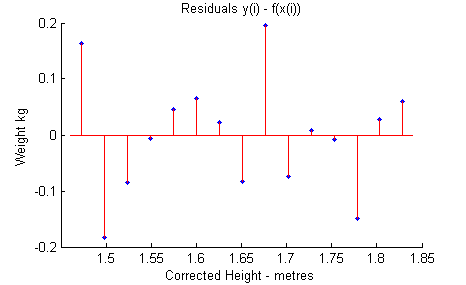
However, a quartic also produces some reduced residuals. Properly, one must consider the question "significant reduction?", not just wander about. So enough of that. Instead, here are some numbers. (With excessive precision, as of course each exactly minimise their data set's sum of squared errors, and we're not comparing observational errors but analysis errors)

            x¹      x²      x³
128.81  -143.16   61.96          Bungled data.
119.02  -131.51   58.50          Corrected data.
408.01   831.24  526.17  118.04  Cubic fit.

As is apparent, the trivial detail of rounding data has produced a significant difference between the parameters of the quadratic fit. So obviously, none of this should be discussed. NickyMcLean (talk) 23:47, 26 May 2008 (UTC)

Analysis of variance

I've just done a series of edits on the analysis of variance section that amount to a semi-major rewrite. Some idiot claimed that the "regression sum of squares" was THE SAME THING AS the sum of squares of residuals, and the error sum of square was NOT the same thing as the sum of squares of residuals. In other words, the section was basically nonsense. Michael Hardy (talk) 12:18, 1 July 2008 (UTC)

Edits July 26, 08

Corrected some errors and misleading text on this page. I clarified that the assumptions that X is fixed and that the error is NID are for simple expositions and that these assumptions are commonly relaxed (the previous text asserted that the case in which the mean of the error term is not zero is "beyond the scope of regression analysis"!) It is not true that the residuals nor the vector of estimates is distributed Student even when we are assuming the errors are normal, and I have corrected these claims. I deleted some of "checking model structure," which was a recipe for the most naive form of data mining. Made a few other small clarifications or corrections. —Preceding unsigned comment added by 68.146.25.175 (talk) 21:15, 26 July 2008 (UTC)

Let's undo this edit from February

Probably the first thing we need to do to clean up this mess is to undo this edit that was done in February. Michael Hardy (talk) 18:37, 28 July 2008 (UTC)

...OK, maybe there were some good things in it, but it's horribly irritating to use non-standard notational conventions. Everything has to change. Michael Hardy (talk) 18:39, 28 July 2008 (UTC)

I don't like the first line

"Linear regression is a form of regression analysis in which the relationship between one or more independent variables and another variable, called dependent variable, is modeled by a least squares function, called linear regression equation."

It's just wrong. Linear regression is a form of regression analysis in which the unknowns (the betas) are a linear (or affine if you prefer) function of the knowns (the response y and the predictors x1, x2,...xn). And what's this "least squares function"? Least squares is not part of the model, it's an estimation method. It's not the only one and is not essential to the definition of linear regression. Blaise (talk) 16:34, 28 August 2008 (UTC)

I don't like it much either. But notice: it's not the betas that are a linear function of the "y"s. The least-squares estimates of the betas are linear in the vector of "y"s, and non-linear in the "x" vectors. You could say the "y"s are linear in the betas, though. Michael Hardy (talk) 21:58, 28 August 2008 (UTC)

Intorduction needs some laymans terms

I don't know a whole lot about statistics, but I've been reading about political polling lately, came across this term and wanted to know more. I usually go to Wikipedia and read at least the opening paragraph for a good introduction on a subject. This article uses jargon in the intro paragraph that doesn't help me at all. Can someone put Linear Regression in laymans terms? —Preceding unsigned comment added by GregCovey (talk • contribs) 23:29, 15 October 2008 (UTC)

Yes, I agree with you. You may find section on regression equation helpful.

TomyDuby (talk) 11:28, 2 November 2008 (UTC)

Error in Definitions?

Shouldn't the first line of Definitions read: "The data consist of n values $X_{i,1},\ldots ,X_{i,n}$" instead of "The data consist of n values $x_{i,1},\ldots ,x_{i,n}$"? Colindente (talk) 13:33, 17 October 2008 (UTC)

I changed the definition some time ago, so the definition now reads $X_{i1},\ldots ,X_{ip}$ (note the use of p to denote the number of regressors, since n is usually used for the number of data points in the sample). As to answer your question, capital letters normally denote random variables and lower case letters constants (scalars). The most general form of regression considers stochastic regressors (hence the use of upper-case letters in the definition), but in many contexts we assume that the regressors are nonstochastic, i.e. that we have a sample of the form $(Y_{i},x_{i1},\ldots ,x_{ip}),i=1,\ldots ,n$. In this case the regression model is written as

$Y_{i}=\beta _{0}+\beta _{1}x_{i1}+\ldots +\beta _{p}x_{ip}+\varepsilon _{i}$

However the nonstochasticity hypothesis can hardly be made in social sciences particularly. Here $\varepsilon _{i}$ is a random variable, despite that it is written in lower case since there is no capital epsilon. Also note that you may sometimes see the model only written in lowercase letters, i.e.

$y_{i}=\beta _{0}+\beta _{1}x_{i1}+\ldots +\beta _{p}x_{ip}+u_{i}$

If one respects the upper-case notation for random variables, then this means that we place ourselves in a nonprobabilistic context where $u_{i}$ is not a stochastic term but only an unobserved difference between the regression plane and the data points. This notation is often used when it comes to estimate parameters on the basis of observations.

Maybe we should make this clearer in the article, since misunderstandings about these slight but important differences are commonplace.

Flavio Guitian (talk) 17:46, 28 November 2008 (UTC)

Flavio, I would like to rise three suggestions how to improve this article.

1. Start with a simple case and progress towards more complicated cases: Specifically, when the idea of linear regression is presented, the xs should be deterministic. Only at the end let us introduce the possibility that the x are random variables.
2. As there are many confusing symbols and similar definitions (regressor and regressand, for example), there should be a chapter with definitions and symbols
3. Let us stick to these symbols and definitions.

What do you think?

TomyDuby (talk) 16:34, 30 November 2008 (UTC)

Well, we could create a new section containing the different synonyms used but there is already in the "Theoretical model" section a statement about the equivalence of these different terms. But maybe we should make this more visible by creating a subsection.... As for the deterministic vs. nondeterministic regressors, the difference is not explicitly stated in the article. At the moment, it is just said that we start from a random sample, which leaves open the possibility of nondeterministic regressors. In this context a deterministic regressor may be viewed as a random variable with zero variance.

What would be a great improvement is the statement of the classical assumptions in mathematical terms. These assumptions are often called the Gauss-Markov assumptions and are fundamental to regression formulated in statistical terms (i.e. not only algebraic regression which only consists of finding the best estimates). This is especially relevant since later in the article there is a section about checking these assumptions. Flavio Guitian (talk) 23:13, 19 February 2009 (UTC)

Layman's summary?

Can we get a layman's definition of this term? —Preceding unsigned comment added by Ken444444 (talk • contribs) 22:53, 18 December 2008 (UTC)

Better picture?

Is nothing better than this picture available?

Example of linear regression with one independent variable.

Its artificiality, in that the errors are uniformly distributed, glares at you the instant you see the page. Michael Hardy (talk) 05:08, 20 January 2009 (UTC)

I see that Oleg has said my accuracy dispute is silly. But this image is really really terrible. Consider attempting to use this image to illustrate the following basic ideas:

• The line used for estimating y based on x and that used for estimating x based on y are, and should be, different from each other.
• Leverage issues such as those discussed at Studentized residual.
• Lack-of-fit sums of squares.

Probably I'll add more examples to this list later. Michael Hardy (talk) 16:56, 21 February 2009 (UTC)

Error Distribution

The conditional distribution of Yi given Xi is a linear transformation of the distribution of the error term.

It is? Seems to me it's a shifted version of the distribution of the error term, which is not a linear transformation. 72.75.126.69 (talk) 02:22, 26 January 2009 (UTC)

That is certainly true. Michael Hardy (talk) 23:58, 17 February 2009 (UTC)