Wikipedia:Reference desk/Mathematics

Welcome to the mathematics section
of the Wikipedia reference desk.

skip to bottom

Select a section:

• Computing
• Entertainment
• Humanities
• Language
• Mathematics
• Science
• Miscellaneous
• Archives

Want a faster answer?

Main page: Help searching Wikipedia

   

How can I get my question answered?

• Select the section of the desk that best fits the general topic of your question (see the navigation column to the right).
• Post your question to only one section, providing a short header that gives the topic of your question.
• Type '~~~~' (that is, four tilde characters) at the end – this signs and dates your contribution so we know who wrote what and when.
• Don't post personal contact information – it will be removed. Any answers will be provided here.
• Please be as specific as possible, and include all relevant context – the usefulness of answers may depend on the context.
• Note:
  • We don't answer (and may remove) questions that require medical diagnosis or legal advice.
  • We don't answer requests for opinions, predictions or debate.
  • We don't do your homework for you, though we'll help you past the stuck point.
  • We don't conduct original research or provide a free source of ideas, but we'll help you find information you need.

Ready? Ask a new question!

How do I answer a question?

Main page: Wikipedia:Reference desk/Guidelines

• The best answers address the question directly, and back up facts with wikilinks and links to sources. Do not edit others' comments and do not give any medical or legal advice.

See also:

• Teahouse
• Help desk
• Village pump
• Help manual

November 22

Letter Combinations

I began wondering how many total ways is there to combine six letters without repeating the same thing in a different order?

For example: A,B,C,D,E,F is one possibility. A,A,A,A,A,A is one possibility. A,A,A,A,A,B is another. B,A,A,A,A,A is merely a repeat of the above. Thus, not a possibility.

I could write a program to figure this out, but I thought I learned in high school a way to figure this out using formulas. I think it is by using the second part of http://en.wikipedia.org/wiki/Combination. Nkot (talk) 00:43, 22 November 2009 (UTC)

There's a far fewer number of ways of arranging 6 letters when all you have to work with is 6 letters, than 6 letters out of 26 or more. Your examples don't go beyond F, so maybe you're only looking at 6 in total, but it's not entirely clear. Maybe using 6 objects rather than 6 letters would make it clearer. When you say "different order", would you consider AAAAAB and AAABAA to be the same result, but just in a different order - or is it only mirror images that you call the same order? -- JackofOz (talk) 01:14, 22 November 2009 (UTC)

I see that I was not very clear. I am talking about choosing 6 letters out of 26 letters in such a way that the letters can be repeated. However, each combination should be unique when the letters within it are ordered alphabetically. The fourth example would be the same as the third example if its letters were ordered alphabetically. Your example as well would not be unique. Thus, neither are possible combinations. Nkot (talk) 01:34, 22 November 2009 (UTC)

You can think of the problem as finding how many ways there are of dividing 6 beads among 26 different bins. We can think of having 25 movable dividers that separate the 26 bins, and we can arrange the dividers and beads in whatever order we want. There are 31 objects and 6 of them are beads, which allows ${31 \choose 6}$ different arrangements. See Stars and bars (probability). Rckrone (talk) 02:29, 22 November 2009 (UTC)

I didn't see the part at the end of the question about the formula at Combination#Number of combinations with repetition. You're right about that being the correct formula. They also explain the stars and bars thing there in different words. Rckrone (talk) 04:16, 22 November 2009 (UTC)

Max symbol

I was looking in Table of mathematical symbols and I don't see a symbol to indicate the maximum value in a set (or the maximum value between two values). I want to write: absolute value of the length of A minus the length of B <= D <= the maximum between the length of A and the length of B. What I have is: ||A|-|B|| <= D <= max(|A|,|B|). I don't like the mixed use of | for both "length of a vector" and "absolute value". I also want to avoid computer programming appearance with max(). -- kainaw™ 05:03, 22 November 2009 (UTC)

Do you mean using $A\wedge B$ for min and $A\vee B$ for max? (Igny (talk) 05:18, 22 November 2009 (UTC))

Those are far from standard notations. --Tango (talk) 07:06, 22 November 2009 (UTC)

Actually $A\wedge B$ and $A\vee B$ for inf and sup of $\{A,B\}$ didn't meet a great success outside the theory of ordered structures and lattices (where they are a standard notation, however). Most likely, the reason is that the symbols $\wedge$ and $\vee$ are already largely and universally used for operations in the exterior algebras. --pma (talk) 09:22, 22 November 2009 (UTC)

They may be obsolete in many fields of math, but I have seen their usage in a number of recent publications on measure theory and probability theory. (Igny (talk) 00:14, 23 November 2009 (UTC))

See for example here, page 4, formula 1.2 (Igny (talk) 01:12, 23 November 2009 (UTC))

The mathematical term for the largest element of a set is supremum, abbreviated sup. But I think that is not what you are asking. We'd usually call the "length of a vector" its norm rather than its absolute value. The norm is denoted $\|x\|$. So you'd write

$|\|A\|-\|B\||\leq D\leq \max(\|A\|,\|B\|)$.

67.117.145.149 (talk) 06:48, 22 November 2009 (UTC)

The largest element in a set is the maximum. The least upper bound of a set is the supremum. They are different things. If a set has a maximum that will also be its supremum, but a set can have a supremum without having a maximum since the least upper bound is not necessarily a member of the set. For example, $\sup[0,1)=1$, but that set has no maximum. --Tango (talk) 06:51, 22 November 2009 (UTC)

Oh yes, good point. 67.117.145.149 (talk) 06:57, 22 November 2009 (UTC)

The standard mathematical notation for a maximum is "max", whether that looks like computer code or not. --Tango (talk) 06:51, 22 November 2009 (UTC)

The J (programming language) uses >. for max and <. for min.

   3 >. 4
4

Bo Jacoby (talk) 08:02, 22 November 2009 (UTC).

Any discontinuous function with standard notation will reduce your problem to one already solved, as long as you define its value at the discontinuity as half-way between the values its jumping between. For example,

$\max\{a,b\}={\frac {a}{2}}({\mbox{sgn}}(a-b)+1)+{\frac {b}{2}}({\mbox{sgn}}(b-a)+1)$.

Expz (talk) 00:51, 23 November 2009 (UTC)

If we wanted to write max in a silly longwinded confusing way, we could write $\max\{a,b\}={\frac {a+b+|a-b|}{2}}$. Algebraist 01:56, 23 November 2009 (UTC)

November 23

An interesting trig problem

Dear Wikipedians:

I'm trying to solve for general and exact solution for the following equation:

sin3x = cos2x

where x is in the domain of (-π,π).

The solution I have so far is as follows:

$\sin 3x=\cos 2x$

$\sin 3x=\sin \left({\frac {\pi }{2}}-2x\right)$ (Equation 1)

AND

$\sin 3x=\sin \left({\frac {\pi }{2}}+2x\right)$ (Equation 2)

Equation 1 yields:

$3x={\frac {\pi }{2}}-2x$

$5x={\frac {\pi }{2}}$

$x={\frac {\pi }{10}}$

and the general solution from equation 1 is:

$x=(2n+1)\pi -{\frac {\pi }{10}}$

AND

$x=2n\pi +{\frac {\pi }{10}}$

Equation 2 yields:

$3x={\frac {\pi }{2}}+2x$

$x={\frac {\pi }{2}}$

and the general solution from equation 2 is:

$x=2n\pi +{\frac {\pi }{2}}$

AND

$x=(2n+1)\pi -{\frac {\pi }{2}}$

So altogether I was able to get all the positive roots π/10, π/2, 9π/10 from the general solution that fits in the domain. However, my graphing calculating clearly shows that there are two more negative roots in the domain: -3π/10, -7π/10. I am at a loss to get these roots from the elegant approaching I am using so far. Is there some way of getting the negative roots from the method I have used above, or do I have to resort to solving nasty high-degree equations?

Thanks for all the help.

70.31.153.35 (talk) 02:09, 23 November 2009 (UTC)

$\sin(\alpha )=\sin(\beta )\Rightarrow \alpha =\beta +2\pi k$ or $\alpha =(2k+1)\pi -\beta$ right? (Igny (talk) 02:26, 23 November 2009 (UTC))

Resolved

Means with logarithmic data

How is the following possible: for group 1, the arithmetic mean of a variable is around 10000, while for group 2 it is around 12000. However, when I transform the variable into logs with base 10, the arithmetic mean for group 1 is greater than for group 2 (and, if I take 10 to these powers, I should get the geometric mean, but then the mean for group 1 is still bigger than group 2. So, looking at the data before transformation I conclude that group 1 is richer (the variable is gdp per capita), but after the transformation I draw the opposite conclusion. —Preceding unsigned comment added by 96.241.9.31 (talk) 05:12, 23 November 2009 (UTC)

On mathematical terms, this is not at all surprising. The arithmetic and geometric means are different things, so obviously you can find a pair of sets of data where the AM of the first is larger while the GM of the second is larger. This usually happens when the first has a higher variance. A simple example is (1, 7) versus (3, 4).

As for the conceptual interpretation - congratulations, you now know How to Lie with Statistics (saying "average" without specifying which kind, while secretly choosing the one that best fits the result you are trying to prove). If you have no interest in lying, the choice of average depends on what you are trying to do - I think AM has more to do with economic prowess, while GM or median are better indicators of overall welfare. -- Meni Rosenfeld (talk) 07:27, 23 November 2009 (UTC)

Thank you, that was exceedingly helpful. —Preceding unsigned comment added by 96.241.9.31 (talk) 13:56, 23 November 2009 (UTC)

dipole moment

this his been used to reference a physics article on electric dipole moment but it doesnt seemt ot follow to me.

http://books.google.com/books?id=LIwBcIwrwv4C&pg=PA81#v=onepage&q=&f=false

the step where he goes

$\phi (r)={\frac {qd\cos(\theta )}{4\pi \epsilon _{0}r^{2}}}={\frac {q\mathbf {d} \cdot \mathbf {r} }{4\pi \epsilon _{0}r^{2}}}$

surely the introduction of a r term on top needs to be cancelled by making the r term on the bottom cubic? —Preceding unsigned comment added by 129.67.39.44 (talk) 12:51, 23 November 2009 (UTC)

Looking closely at the link you gave, I see there is a "hat" over the r, which means it is a unit vector

${\boldsymbol {\hat {r}}}={\frac {\boldsymbol {r}}{\|{\boldsymbol {r}}\|}}$

so we have

$\phi (r)={\frac {qd\cos(\theta )}{4\pi \epsilon _{0}r^{2}}}={\frac {q\mathbf {d} \cdot \mathbf {\hat {r}} }{4\pi \epsilon _{0}r^{2}}}$

which is correct. Gandalf61 (talk) 13:22, 23 November 2009 (UTC)

Transpose and tensors

I posed a question on Talk:Transpose that didn't get any responses there. Perhaps this is a better audience since it's a bit of an essoteric question for such an elementary topic; Here's the question again:

I'm confused. It seems like much of linear algebra glosses over the meaning of transposition and simply uses it as a mechanism for manipulating numbers, for example, defining the norm of v as $\|v\|={\sqrt {v^{\top }v}}$.

In some linear-algebra topics, however, it appears that column and row vectors have different meanings (that appear to have something to do with covariance and contravariance of vectors). In that context, the transpose of a column vector, c, gives you a row vector -- a vector in the dual space of c. I think the idea is that column vectors would be indexed with raised indices and row vectors with lowered indices with tensors.

Here's my confusion: If row vectors and column vectors are in distinct spaces (and they certainly, even in elementary linear algebra in that you can't just add a column to a row vector because they have different shapes), then taking the transpose of a vector isn't just some notational convenience, it is an application of a nontrivial function, $f(v)=v^{\top }:V\rightarrow V^{*}$. To do something like this in general, we can use any bilinear form, but that involves more structure than just

So:

1. Is it correct that there are are two things going on here: (1) using transpose for numerical convenience and (2) using rows versus columns to for indicateng co- versus contravariance?
2. Isn't the conventional Euclidean metric defined with a contravariant metric tensor: $\|v\|={\sqrt {g_{ij}v^{i}v^{j}}}$? Doesn't that not involve any transposition in that both vs have raised indices?

Thanks. —Ben FrantzDale (talk) 14:16, 23 November 2009 (UTC)

I guess it depends on how we define vectors. If we consider a vector as just being an n by m matrix with either n=1 or m=1, then transposition is just what it is with any other matrix - a map from the space of n by m matrices to the space of m by n matrices. --Tango (talk) 14:38, 23 November 2009 (UTC)

Sure. I'm asking because I get the sense that there are some unwritten ruels going on. At one extreme is the purely-mechanical notion of tranpose that you describe, which I'm happy with. In that context, transpose is just used along with matrix operations to simplify the expression of some operations. At the other extreme, rows and columns correspond to co- and contra-variant vectors, in which case transpose is completely non-trivial.

My hunch is that the co- and contravariance convention is useful for some limited cases in which all transformations are mixex of type (1,1) and all (co-) vectors are either of type (0,1) or (1,0). But that usage doesn't extend to problems involving things like type-(0,2) or type-(2,0) tensors since usual linear algebra doesn't allow for a row vector of row vectors. My hunch is that in this case, transpose is used a kludge to allow expressions like $g_{ij}v^{i}v^{j}$ to be represented with matrices as $v^{\top }gv$. Does that sound right, or am I jumping to conclusions? If this is right, it could do with some explanation somewhere. —Ben FrantzDale (talk) 15:13, 23 November 2009 (UTC)

Using an orthonormal basis, $\scriptstyle g_{ij}=\delta _{ij}\,$, and $\scriptstyle g_{ij}v^{i}v^{j}=(g_{ij}v^{i})v^{j}=(\delta _{ij}v^{i})v^{j}=v_{j}^{\top }v^{j}=v^{\top }v.$ That "usual linear algebra doesn't allow for a row vector of row vectors" is the reason why tensor notation is used when a row vector of row vectors, such as $\scriptstyle g_{ij}\,$, is needed. Bo Jacoby (talk) 16:53, 23 November 2009 (UTC).

Also note that there is no canonical isomorphism between V and V* if V is a plain real vector space of finite dimension >1, with no additional structure. What is of course canonical is the pairing VxV* → R. Fixing a base on V is the same as fixing an isomorphism with Rⁿ, hence produces a special isomorphism V→V*, because Rⁿ does possess a preferred isomorphism with its dual, that is the transpose, if we represent n-vectors with columns and forms with rows. Fixing an isomorphism V→V* is the same as giving V a scalar product (check the equivalence), which is a tensor of type (0,2), that eats pairs of vectors and defecates scalars. --pma (talk) 18:46, 23 November 2009 (UTC)

Those are great answers! That clarifies some things that have been nagging me for a long time! I feel like It is particularly helpful to think that conventional matrix notation doesn't provide notation for a row of row vectors or the like. I will probably copy the above discussion to Talk:Transpose for postarity and will probably add explanation along these lines to appropriate articles.

I haven't worked much with complex tensors, but your use of conjugate transpose reminds me that I've also long been suspiscious of its "meaning" (and simply that of complex conjugate) for the same reasons. Could you comment on that? In some sense $c^{*}c$ on a complex number, $c=a+bi$ is the same operation as $v^{\top }v$ on a vector, using conjugate transpose as a mechanism to compute $c^{*}c=a^{2}+b^{2}$. For a complex number, I'm not sure what would generalize to "row vector" or "column vector"... I'm not sure what I'm asking, but I feel like there's a little more that could be said connecting the above great explanations to conjugate transpose. :-) —Ben FrantzDale (talk) 19:19, 23 November 2009 (UTC)

A complex number (just as a real number) is a 1-D vector, so rows and columns are the same thing. The modulus on $\mathbb {C}$ can be thought of as a special case of the norm on $\mathbb {C} ^{n}$ (ie. for n=1). From an algebraic point of view, complex conjugation is the unique (non-trivial) automorphism on $\mathbb {C}$ that keeps $\mathbb {R}$ fixed. Such automorphisms are central to Galois theory. I'm not really sure what the importance and meaning is from a geometrical or analytic point of view... --Tango (talk) 19:41, 23 November 2009 (UTC)

Let V and W be two vector spaces, and ƒ : V → W be a linear map. Let F be the matrix representation of ƒ with respect to some bases {v_i} and {w_j}. I seem to recall, please do correct me if I'm wrong, that F : V → W and F^T : W* → V* where V* and W* are the dual spaces of V and W respectively. In this setting v^T is dual to v. So the quantity v^Tv is the evaluation of the vector v by the covector v^T. ~~ Dr Dec (Talk) ~~ 23:26, 23 November 2009 (UTC)

Goldbach's conjecture

Several weeks ago I saw a Wikipedia web page where one could submit a "proof" of Goldbach's conjecture. However, not having any proof to submit, I didn't pay attention to the page's URL, and have forgotten it. Does anyone know how to reach this page, or has it since been deleted?Bh12 (talk) 15:19, 23 November 2009 (UTC)

Wikipedia is definitely not the place to submit proofs (or "proofs") of new results. If such a page existed on Wikipedia, it indeed would (or should) have been deleted, though chances are that you actually saw it on a different site (maybe using the MediaWiki software). — Emil J. 17:27, 23 November 2009 (UTC)

Square of Opposition and "The subcontrary of the converse of the altern of a FE is T"

I have a question that emerged from a basic logic class I am taking. Forgive me if this isn't the right desk section, but I'm honestly confused on whether to stick this under math, humanities (philosophy), or miscellaneous. It seems to me that this section is most appropriate.

We have been taught the traditional Square of Opposition. We were given statements like the following, and asked to use the square to them label "true" or "false:"

(1) The converse of the altern of a TA proposition is UN.

(2) The contradictory of the converse of a FA proposition is T.

(3) The contrary of the converse of a TE is F.

A, E, I, and O stand for types of propositions (see here ), T stands for true, F stands for false, and UN for unknown truth value. T or F before a letter means a true or false proposition of that type (FO means a false O claim). For these exercises, we are obviously going by traditional Aristotelian logic, in which e.g. A claims are taken to imply I claims.

Using the Square, we know that (1) is false, (2) is considered false because the truth value is UN, not T, and (3) is true. That's not the problem.

The problem crops up when we deal with something like the following, a problem that I devised:

(4) The subcontrary of the converse of the altern of a FE is T.

I believe that (4) is true. My reasoning: Whenever we have a FE, we have a TI (contradictories). An "I" claim has an interchangeable converse ("some S is P" also means "some P is S"). The altern of an FE is an O of unknown truth value. The converse of that O ("some P is not S") will be unknown as well, of course. But the subcontrary of the converse of the O is the same as the converse of the I. We know that "some P is S" (the converse of the I) is T. So, we know that the subcontrary of the converse of the altern of a FE is T. Therefore, I believe (4) should be marked "true."

However, I presented my reasoning for (4) above, and my logic professor disagrees with me. She points out that the altern of a FE proposition is UN, and the converse of an O is also UN. As far as I can understand, she says that whenever one runs into an UN, one cannot move any further. So she teaches that (4) is false, for the truth value is UN, not T. I'm afraid I can't quite see her reasoning. I am curious to find a third opinion.

So, do you agree or disagree with my result? Please explain your reasoning. I can go into more detail about my own, but this question is already a little long. 99.174.180.96 (talk) 18:40, 23 November 2009 (UTC)

Oh.. I do not have an answer; actually I'm not even sure I understand, but this brings me back to my childhood, when they made us learn by hart Barbara, Celarent, Darii, Ferio,... and if you weren't ready, it was whips! I never managed to understand that stuff :-( Elementary school was a hard life for a kid, those times. Anyway, hope somebody has some more factual hint. --pma (talk) 23:18, 23 November 2009 (UTC)

Ok, I'm trying to understand this. By "The subcontrary of the converse of the altern of a FE is T" do you mean that "No S is P" is false implies that "Some P is S" is true? If you know how to express this in terms of set theory (if that's even possible) it would make more sense to me. Jkasd 08:11, 24 November 2009 (UTC)

Try to translate into a more modern notation. Consider the probability that a random P is S, x=|S|/|P|, assuming |P|>0. Then the A-claim "all S are P" means x=1. The E-claim "No S is P" means x=0. The I-claim "Some S is P" means x>0 and the O-claim "some S is not P" means x<1. Bo Jacoby (talk) 08:51, 24 November 2009 (UTC).

99.174.180.96 - I agree with your reasoning. If "No S is P" is false then some S is P, and therefore some P is S. If "No S is P" is false then you cannot conclude anything about the truth value of "Some S is not P", but that does not mean you cannot conclude anything about the truth value of "Some S is P" or "Some P is S". Your teacher may be interested in the new-fangled ideas of Mr. Boole and Mr. Venn, who claim to have reduced logic to simple algebra. Gandalf61 (talk) 11:36, 24 November 2009 (UTC)

This is the OP speaking--Thanks for your replies. I'm sorry that my post was hard to understand.

pma: thanks for the story. :)

Jkasd: Yes, in response to your question, I believe that

The subcontrary of the converse of the altern of a FE is T

means that

"No S is P" is false implies that "Some P is S" is true

However, I cannot be 200% sure of that inference as a PhD-level professor of philosophy believes that I have gone wrong somewhere, and if she's right, something must be wrong with my logical insight into this problem. :)

I strongly suspect that someone could express my problem in terms of set theory. I'm afraid that I don't know how, though. Part of the difficulty is that there are puzzles regarding the "existential import" of the propositions of Aristotelian logic. To the extent that I know what that means, I know that I can't be confident in trying to shift between the two. But thanks for your time.

Bo Jacoby: I'm sorry, but I'm confused. You say "Consider the probability that a random P is S" (remember, P before S). But if all S is P (S before P), then that probability is not necessarily 1. There may still be plenty of P that is not S, so there is no certainty that a random P is S. It's "all P is S" that gives x = 1. I think either you got something backwards or I don't understand your probability equations correctly.

Sorry for spreading confusion. I probably ment to write "Consider the probability that a random S is P" (S before P). Does that make sense? Bo Jacoby (talk) 23:12, 25 November 2009 (UTC).

Gandalf61: Thank you for your input. I should be fair to my teacher: we're not learning only pure traditional Aristotelian logic. We have done stuff with sentential variables and propositional logic, and are familiar with Venn diagrams. It's only a first year course. 99.174.180.96 (talk) 14:48, 24 November 2009 (UTC)

Set theory representation here is straightforwrd. "No S is P" can be expressed as $S\cap P=\emptyset$ ("S intersection P is empty"). So ""No S is P" is false" becomes $S\cap P\neq \emptyset$ ("S intersection P is not empty"). But this is exactly the same as the representation of "Some S is P", and as "Some P is S". So all three statement are equivalent. With respect to all concerned, I think part of the difficulty may be that your professor is a professor of philosophy, not a professor of mathematics. Gandalf61 (talk) 15:45, 24 November 2009 (UTC)

Oh yeah. For some reason I was trying to think in terms of subsets and set membership. Jkasd 08:32, 25 November 2009 (UTC)

£1,250 million

How many digits should this number have? I interpret it as 1,250,000,000. A version of the assertion is found here[1] (search for "million"). Long and short scales doesn't seem to cover this, which is more about how to write down numbers than their actual definition.   Will Beback  talk  23:55, 23 November 2009 (UTC)

Unless I'm misunderstanding your question, it most certainly is covered in that page. The long and short scales both agree that 1 million is 1,000,000. Where they start to disagree is at 1 billion, which is 1,000,000,000 in the short scale and 1,000,000,000,000 in the long scale. --COVIZAPIBETEFOKY (talk) 01:56, 24 November 2009 (UTC)

Alternatively, they both agree that 6 zeros is a million, 7 zeros is ten million, and 8 zeros is a hundred million. Where they start to disagree is nine zeros... 92.230.68.236 (talk) 15:59, 24 November 2009 (UTC)

But either way—long or short scale—1,250 million is 1,250,000,000. So the long-versus-short-scale issue doesn't seem to bear on that question. Michael Hardy (talk) 02:47, 24 November 2009 (UTC)

It is only an issue if you choose to interpret the comma as a european decimal point. -- SGBailey (talk) 16:57, 24 November 2009 (UTC)

very creative, but no one would write a trailing zero in that case. 92.230.68.236 (talk) 17:49, 24 November 2009 (UTC)

Of course one could. A trailing zero in this case would be a perfectly usual way of specifying that the number has four significant digits. — Emil J. 18:04, 24 November 2009 (UTC)

SGBailey: Us Brits are "Europeans", but we don't use a comma as a decimal point. We write ½ as 0.5 and 10⁵ as 100,000. ~~ Dr Dec (Talk) ~~ 18:53, 24 November 2009 (UTC)

In case anyone is interested in which notation different countries use, wikipedia has the article Decimal separator. Aenar (talk) 19:19, 24 November 2009 (UTC)

Thanks for the replies. I got hold of the original paper (written by Americans, but concerning the UK and published in the Netherlands). The calculation is £5,000 * 255,000 = £1,275,000,000.   Will Beback  talk  21:14, 24 November 2009 (UTC)

November 24

why does anyone bother with axioms since Goedel?

Ever since Goedel proved that the truth about a system will be a superset of the things you can show with your self-consistent axioms, why would anyone bother trying to start from a set of axioms and work their way through rigorously? Doesn't this reflect that they are less interested in the whole truth than in the part of it they can prove? Wouldn't it be akin to sweeping only around streetlamps (where the lit section is that part of the truth about your system which your axioms can prove), and leaving the rest of the street (the other true statements) untouched? For me, this behavior borders on a wanton disregard for discovering the whole truth (cleaning the whole pavement), and I don't understand why anyone bothers with axioms since Goedel. Any enlightenment would be appreciated. 92.230.68.236 (talk) 15:54, 24 November 2009 (UTC)

What is the alternative? Give up on maths altogether? You can't prove anything without some premises and proof is what maths is all about. --Tango (talk) 15:57, 24 November 2009 (UTC)

“

Thanks for the quick answer, but are you quite certain that rigorous proof is what maths is all about, rather than becoming as confident as you are able about the truth regarding all parts about a system, by whatever means?

Granted, you will be less sure of the unlit areas (you may have empirically strong evidence for your conjecture, but the conjecture may lie outside of what you can prove), but my question really is as I phrased it: doesn't an exclusionary fascination with the part of truth your axioms can prove in some way show a disregard for the whole truth?

After all, statistically speaking you can become more and more confident in things you can't prove, but it doesn't come for free - it takes real scientific effort (usually number-crunching). Perhaps you would not call such research mathematics? Why, when despite its lack of rigor -- a rigor which can even theoretically only reach a subset of the truth -- this research is engaged in finding out the truth about an abstract system? I fail to see why this research should fall outside of the field of mathematics.

In my analogy: when you clean the pavement, your goal is to reduce the dirt etc piled up everywhere on it (let's call this the truth, when you learn it by deduction or empirically you pick it up). Granted when you do mathematics empirically, you may leave some truth on the pavement, but isn't it better to have empirical truth from everywhere (pick up what you can from every part of the pavement) than to have all the possible truth (since you've proved it) from just the lit areas?

For me, it's hard to see why only the latter and not the former should be considered mathematics, unless of course the goal of mathematics is not to pick up all the truth about a system at all, but rather to just fiddle with the lights to change how much/what is lit depending on your axioms, and then clean up as much as you can from just there?

As I said above, for me this almost implies a disregard for the truth itself: for actually cleaning every part of the pavement to whatever extent you can; instead this view seems to focus neurotically on the part of the truth you can be 100% sure of picking up entirely, without any chance of being wrong, or leaving any statistical confidence (a kind of truth) on the ground: you don't just sweep the lit area, you mop it as well, all the while not even sweeping the unlit area.

In sum: why do you propose that only mopping the pavement in lit areas should be mathematics, and not sweeping the unlit areas (empirical evidence-gathering, which will never "prove" anything)? I just can't see any reason for your statement "proof is what maths is all about" unless you just have no regard for truth, but only for proof (no regard for cleaning the pavement, but for only mopping the lit parts so well you can eat off of them). Any justification for your statement you can offer would be very appreciated. 92.230.68.236 (talk) 16:27, 24 November 2009 (UTC)

Also: if it's not math, then what do you call mathematical-like evidence gathering? Do you call it physics, even if it is purely about an abstract system? Or do you just call it "unscientific", as for you science is only the truth you can rigorously prove, rather than the properties of the system -- the truth, if you will - that your research suggests? If this is unscientific, then Einstein never did a day of science in his life: he famously said that no number of experiments could ever prove his theories right, but that a single reproduceable experiment could prove them wrong... I don't see how you can view physics as scientific, but mathematical-like activities outside of proofs unscientific, and if they are not unscientific but scientific, what field do they belong to? Any reasons you have for not saying "mathematics" would be appreciated. 92.230.68.236 (talk) 16:32, 24 November 2009 (UTC)

”

Math is not, strictly, a science, or at least not a natural science. Strict proof is a concept that is quite foreign to all empirical sciences. Your quest for "the whole truth" is unattainable (as shown by Goedel), so we stick to what we can show. And we can, of course, step outside any given system and use reasoning on a meta-level to show things that are unprovable in the original system. Of course our meta-system will have the same basic shortcoming. But what if we are not interested in "truth", but in "provable truth"? What we can prove has a chance to be useful - because it is provable. I'd rather have my bridge design checked by (incomplete) analysis that by (complete) voodoo. --Stephan Schulz (talk) 16:44, 24 November 2009 (UTC)

Thanks, let me ask for a clarification on your word "unattainable". If the task is to find out which of 10 normal-looking coins is heavily weighted on one side only by flipping them (as many times as you want), would you call the truth in this situation "unattainable" in the same sense you just used? I mean, you can become more and more confident of it, but your conjecture will never become a rigorous proof. 92.230.68.236 (talk) 16:57, 24 November 2009 (UTC)

Well, your confidence is bounded not by certainty, but by certainty within your model of reality. What if there is an invisible demon who always flips one coin to head? What if you're living in the Matrix and the coins are just simulations? No matter what tools you are allowed to use, or how many witnesses there are, you cannot make statements about "the real world" with absolute certainty. This is a fundamental divide that separates math from the empirical sciences. --Stephan Schulz (talk) 17:41, 24 November 2009 (UTC)

To my mind it wasn't Goedel who so much as Russell's paradox that shook up mathematics. It didn't say math might be inconsistent but that math, as understood at the time, was inconsistent. I have visions of accounting firms going on holiday until it was resolved because no one could be sure that sums would still add up the same from one day to the next.--RDBury (talk) 16:30, 24 November 2009 (UTC)

You might be interested in Experimental mathematics. There is also quite a bit of maths where people have shown under fairly straightforward conditions that something is probably true. Riemann's hypothesis is an interesting case where people aren't even sure if it is true and yet there are many theorems which are proven only if it is true. Another interesting case is the Continuum hypothesis where people have been debating whether there are axioms which would be generally accepted which make it true or false. So basically mathematicians do look at things they can't or haven't been able to prove but they consider them unsatisfactory until a proof is available. Dmcq (talk) 17:10, 24 November 2009 (UTC)

Thank you. Is it fair to say that Tango and S. Schulz above would probably say experimental mathematics isn't in some sense "real" mathematics? 92.230.68.236 (talk) —Preceding undated comment added 17:28, 24 November 2009 (UTC).

Experimental maths is part of maths, but you haven't really finished until you have proven your result (or proven it can't be proven). Empirical evidence helps you work out what to try and prove, but it isn't enough on its own. --Tango (talk) 17:51, 24 November 2009 (UTC)

I don't understand in what way experimental mathematics as described in that article shows that something is probably true. How does one quantify the probability? It looks to me like just plain numerically-based conjectures, an ancient part of mathematics. 67.117.145.149 (talk) 21:21, 24 November 2009 (UTC)

If your conjecture about the natural numbers, say, is satisfied for the first billion natural numbers then that suggests it is probably true for all of them. I'm not sure you can quantify that, though - you would need a figure for the prior probability of it being true before you started experimenting, and I don't know where you would get such a figure. --Tango (talk) 23:52, 24 November 2009 (UTC)

I think when working with mathematics that the general experience is that most questions that mathematians are interested in can be decided by either proving or disproving them. So even though there exist propositions that can neither be proven or disproven, they seem seldomly to come up in practise. Of course we don't know if this impression will change in the future. Aenar (talk) 17:57, 24 November 2009 (UTC)

I have the same impression. Is it fair to say that a mathematician thinks it's better to "decide" (prove or disprove) one unproven proposition than become very confident statistically in ten different ones whose true-value had been unknown? Maybe I'm just ignorant and the latter doesn't really happen in practice (by stark contrast with every other science) - is that it? 92.230.68.236 (talk) 18:10, 24 November 2009 (UTC)

I wouldn't say that to "decide" is the same as prove (or disprove). I decided to have toast for breakfast this morning. Mathematicians discover and then prove. Mathematicians would rather prove something, but it isn't unknown for them to assume something that is very probably true as being true; take the Riemann hypothesis or Goldbach's conjecture for example. There are many results based on these propositions indeed being true. Although, to be honest, this doesn't sit very well with me. It seems to be too much like a house of cards for my liking. The beauty of mathematics is its truth and certainty. The problem with "the other sciences" is that you could conduct an experiment 1,000 times and get one result, and then on the 1,001^st time get a different result: nothing is certain. ~~ Dr Dec (Talk) ~~ 18:31, 24 November 2009 (UTC)

I might have used the word "decide" incorrectly; English is not my mother tongue. I used it (approximately) in the same way as in the article Decision problem. Aenar (talk) 22:48, 24 November 2009 (UTC)

Indeed. There is a big difference between being 99.9999999999% sure that the next apple to fall from the tree in my garden will fall down, rather than up, and being 100% sure that the square of the hypotenuse of a right angled triangle is equal to the sum of the squares of the other two sides. The difference is precisely the difference between science and maths. --Tango (talk) 18:48, 24 November 2009 (UTC)

I don't know. (My first impulse would be that that is not fair to say.) I believe in many cases it might actually be very hard to find a way to apply techniques of experimental mathematics. An example would be if one is trying to prove the existence of an abstract mathematical object which has certain properties. Aenar (talk) 18:38, 24 November 2009 (UTC)

Experiments are fine, but you cannot usually generalize usefully from them in maths. For any arbitrarily large finite set of test values from, say, the natural numbers, I can give you a property that is 100% true on the test values, but whose overall probability to be true is zero (one such property is "P(x) iff x<= m, where m is the largest of your test values). --Stephan Schulz (talk) 18:44, 24 November 2009 (UTC)

To clarify my example which was probably unclear: I was thinking of the object as being (for example) a topological space or another topological/geometric object, where there's no way to enumerate the possible candidate objects. Besides that, I agree with Stephan Schulz. Actually, I'm not sure what I think. Aenar (talk) 18:53, 24 November 2009 (UTC)

In some fields experiments can be very useful (number theory, for example). In others, they are largely useless. --Tango (talk) 18:48, 24 November 2009 (UTC)

I don't think mathematics has ever been about "the whole truth" or even "the part of it that they can prove". It's about the part that's meaningful and satisfying, which most of the time turns out to be provable. Very complex true statements (as shown by Chaitin and so forth) are usually unprovable but also tend to be too complicated for our tiny minds to ascribe meaning to. The statements applicable to traditional science (physics, etc.) turns out (according to Solomon Feferman) to mostly be provable in elementary number theory (Peano arithmetic).[2] You might like a couple of his other papers including "Does mathematics need new axioms?". 67.117.145.149 (talk) 21:38, 24 November 2009 (UTC)

In my view mathematics is an experimental science; the differences from the physical sciences are largely ones of degree (and subject matter). It's true that there is a very old tradition of Euclidean foundationalism according to which mathematics is restricted to statements provable from axioms, but this is ultimately unsatisfactory because it does not give an account of why we choose one set of axioms over another. An extreme mathematical formalist view holds that the axioms are essentially arbitrary, but this, frankly, is nonsense on its face.

A more effective way to think of mathematical statements (more effective in the sense that you'll get more and more useful results) is that they describe the behavior of genuine objects, naturals and reals and sets and so on, and that we want axioms that say true things about those objects, rather than false things. Beyond the simplest statements, which axioms are true as opposed to false is not always self-evident or immediately accessible to the intuition, and therefore the investigation gains an empirical component.

For one example, Gottlob Frege's formalized version of set theory (Will Bailey says Frege didn't talk about sets per se; I have to look into that) was on its face not an unreasonable hypothesis, but it was utterly refuted by Russell's paradox. The modern conception of set theory, based on the von Neumann hierarchy, has not been refuted. This is an empirical difference.

Continuing along these lines, perhaps the most clearly empirical investigation into mathematical axiomatics since the 1930s has been the program of large cardinal hypotheses. The empirical confirmation/disconfirmation of these is not purely restricted to finding contradictions (though a couple of these hypotheses have been refuted in this way); there is also the intricate interplay between large cardinals and levels of determinacy and regularity properties of sets of reals.

Peter Koellner has written a truly excellent paper called On the Question of Absolute Undecidability, which I won't link in case there are any copyright issues but which you can find in five seconds through Google. I cannot recommend this paper enough for anyone interested in these questions; in addition to its other merits it has a great summary of these developments in the 20th century. --Trovatore (talk) 22:11, 24 November 2009 (UTC)

As regards the original question: Rather than "why do we sweep only around the streetlights?" I think a better analogy might be "why do we drive cars, when they can't go on water?". It's certainly true that, whatever the currently accepted axioms might be, there will be things we'd like to know that those axioms can't tell us. But there are also things we'd like to know that we can deduce from the axioms. Should we say that, because we can't do everything, we should therefore do nothing?

You might ask, OK, but you (Mike) say that we have ways of investigating the truth of statements that are not decided by a given set of axioms. Why not use those methods directly on whatever new question whose truth we'd like to know?

The reason is that such investigations are much more difficult, and their outcomes much more arguable, than deduction from established axioms. And moreover, deductive reasoning is a major part of these investigations, so you're not going to get rid of it.

The 100% certainty Tango claims is an illusion and always has been. Nevertheless, once in possession of a proof, we can circumscribe the kinds of error that are possible: The only way the statement can fail to be true is if there is an error in the axioms, or an error in the proof. An error in the axioms is always possible, but the axioms are not that many, and they have a lot of eyes on them; their justifications can be discussed in very fine detail. An error in the proof is also possible, but if any intermediate conclusion looks suspect, it is possible to break down that part of the proof into smaller pieces until an agreement can be reached as to whether it is sound. These things do not have to be perfect in order to be useful. --Trovatore (talk) 23:31, 24 November 2009 (UTC)

"Error in the axioms" arguably makes no sense. They may fail to model your common-sense idea, but they are correct by definition. Formally, a theorem is always of the form Ax -> C, where Ax are the axioms, and C is the conjecture. Pythagoras' theorem, for example, implicitly assumes the axioms of planar trigonometry - it's wrong on a sphere. --Stephan Schulz (talk) 09:48, 25 November 2009 (UTC)

But if we're interested in more than "formally" (which we are), then axioms can most definitely be wrong. You can formally stipulate an axiom 1+1=3, but it is wrong in the sense that it does not correctly describe the behavior of the underlying Platonic objects 1, 3, and plus. Of course you can give the symbols 1, 3, and +, different interpretations in some structure, but in the context we're discussing here, there is only one correct structure to interpret the symbols in. --Trovatore (talk) 10:00, 25 November 2009 (UTC)

What is that one correct structure? Taemyr (talk) 10:10, 25 November 2009 (UTC)

The natural numbers, of course. --Trovatore (talk) 10:16, 25 November 2009 (UTC)

What about useful structures like N₅ (or N₂₅₆ or N_2³²), which interpret the same symbols differently? --Stephan Schulz (talk) 10:53, 25 November 2009 (UTC)

If you mean $\mathbb {Z} /5\mathbb {Z}$, you have to say so. Many languages have a default interpretation. Admittedly in this case we could have been interpreting the symbols in, say, the integers, rather than the naturals, which while it would have agreed on the outcome would have been strictly speaking a different interpretation.

But all of this is a quibble; of course languages can be given different interpretations. The point is that when we have a well-specified intended interpretation, which we normally do, then it is not the axioms that define the truth of the propositions. Rather, the axioms must conform to the behavior of the intended interpretation. If they don't, they're wrong. --Trovatore (talk) 17:50, 25 November 2009 (UTC)

What is exactly Sine, Cosine, and Tangent.

I understand how to use Sine, Cosine, and Tangent but I don't understand what they are. Like when I type in sin(2) in the calcuator, what is the calculator doing to it? How does it arrive at this? —Preceding unsigned comment added by 71.112.219.219 (talk) 18:48, 24 November 2009 (UTC)

The exact values of sin(x), cos(x) and tan(x) are given by the ratios of the lengths of the sides of a right-angled triangle. See this section of the right-angled triangle article for the definitions. As for the calculator, well it could be using Taylor series to work out the value of sin(x). Certain nice values of x have simple answers, e.g. sin(0) = 0, sin(π/4) = 1/√2, sin(π/2) = 1, etc. If you asked your calculator to work out sin(x₀) then it might find and the closest nice value and then substitute your x into the Taylor series of sine, expanded about the nice value. The reason for changing the expansion point is that the Taylor series converges to sin(x₀) faster when the expansion point is closer to x₀.

(ec - with Tango's comment below) As an example, let's choose sin(0.1). Well 0.1 is very close to 0. So we expand sin(x) as a Taylor series about x = 0:

$\sin(x)\sim x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \ .$

So sin(0.1) ≈ 0.1 − 0.001/6 + 0.00001/120 − 0.0000001/5040 + …. Now, these terms get very small, very quickly. For example, the last term is roughly 1.98×10⁻¹¹; so without any effort we have a value accurate to many decimal places. Since n! gets very large, very quickly, we don't need to add many terms before we can an answer accurate to many decimal places. So your calculator could use a bit of addition, subtraction, multiplication and division. ~~ Dr Dec (Talk) ~~ 19:03, 24 November 2009 (UTC)

I'm not sure there is a need to find a good starting point. You'll get enough accurate digits after 5 or 6 terms for any $x\in [-\pi ,\pi ]$ (and any other x can be calculated by taking it modulo pi), and it doesn't take long to calculate 5 or 6 terms. --Tango (talk) 19:14, 24 November 2009 (UTC)

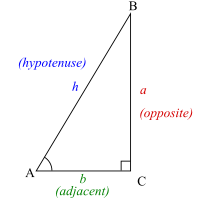
(ec) There are various definitions, but most simply they are ratios of lengths of sides of right-angled triangles. sin(2) is the ratio of the opposite and the hypotenuse of a right-angled triangle with an angle of 2 units (either degrees or radians). Your calculator probably calculates it using a series, such as the Taylor series for sine, which is:

$\sin(x)=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\dots$

The more terms you calculate, the more accurate an answer you get, so the calculator will calculate enough terms that all the digits it can fit on its screen are accurate. Alternatively, it might have a table of all the values stored in its memory, but I think the series method is more likely for trig functions. --Tango (talk) 19:09, 24 November 2009 (UTC)

These illustrations from the article titled trigonometric functions are probably better suited to answer this questions than are the ones in the right-triangle article:

The sine, tangent, and secant functions of an angle constructed geometrically in terms of a unit circle. The number θ is the length of the curve; thus angles are being measured in radians. The secant and tangent functions rely on a fixed vertical line and the sine function on a moving vertical line. ("Fixed" in this context means not moving as θ changes; "moving" means depending on θ.) Thus, as θ goes from 0 up to a right angle, sin θ goes from 0 to 1, tan θ goes from 0 to ∞, and sec θ goes from 1 to ∞.

The cosine, cotangent, and cosecant functions of an angle θ constructed geometrically in terms of a unit circle. The functions whose names have the prefix co- use horizontal lines where the others use vertical lines.

Michael Hardy (talk) 04:08, 25 November 2009 (UTC)

I think it's more likely that the calculator will use the CORDIC algorithm to calculate the values of trig (and other) functions. AndrewWTaylor (talk) 18:19, 25 November 2009 (UTC)

Are you sure? By the looks of the article the method looks a lot more complicated then evaluating a polynomial. ~~ Dr Dec (Talk) ~~ 23:39, 25 November 2009 (UTC)

Evaluating a polynomial is much harder if the chip does not have a hardware multiplier (which used to be, and maybe still is for all I know, fairly typical for pocket calculators). — Emil J. 11:27, 26 November 2009 (UTC)

Eponyms

Does anyone know after whom were the Dawson integral and the Bol loop named? Those two seem to be among the few wiki-articles on eponymous mathematical concepts, where there is no hint about their eponym. --Omnipaedista (talk) 22:00, 24 November 2009 (UTC)

Bol loops were introduced in G. Bol's 1937 paper "Gewebe und Gruppen" in the Mathematische Annalen, volume 11, with reviews and e-prints at: Zbl 0016.22603 JFM 63.1157.04 MR1513147 doi:10.1007/BF01594185. de:Gerrit Bol has a biography with sources. His students are listed on the page for Gerrit Bol at the Mathematics Genealogy Project. JackSchmidt (talk) 22:22, 24 November 2009 (UTC)

Thanks for the detailed answer. I suspected it was Gerrit Door Bol but I couldn't find the title of the original paper or any related information in order to verify it. As for Dawson's integral, it'd be great if someone knowledgeable on the literature of mathematical analysis could indicate where it appeared for the first time or at least Dawson's full name. --Omnipaedista (talk) 22:38, 24 November 2009 (UTC)

Good question! I wasn't able to find a specific reference but my current theory is that it is John M. Dawson.

This article gives a couple of references for the Dawson integral, the earlier of which is:

[Stix, 1962] T. H. Stix, “The Theory of Plasma Waves”, McGraw-Hill Book Company, New York, 1962.

Thomas H. Stix (more info) was a part of Project Matterhorn (now Princeton Plasma Physics Laboratory) from around 1953 to around 1961. In 1962 he was appointed as a professor at Princeton and wrote the above book.

This article references both Stix's book and an article by a J.M. Dawson. That article is:

Dawson, J. M., "Plasma Particle Accelerators," Scientific American, 260, 54, 1989.

That paper appears on the selected recent publications list of John M. Dawson. Dawson earned his Ph.D in 1957, and was a part of Project Matterhorn from 1956 to 1962. His top research interest is listed as Numerical Modeling of Plasma. -- KathrynLybarger (talk) 01:38, 25 November 2009 (UTC)

November 25

True or false?

For every Lebesgue integrable function f, there exists a Riemann integrable function g such that f=g almost everywhere.

Is the previous statement true or false? If false, can you give a counterexample? This is not homework; I'm just curious. Thanks, --COVIZAPIBETEFOKY (talk) 00:32, 25 November 2009 (UTC)

Our article Riemann integral has the answer: the statement is false, and the indicator function of the Smith–Volterra–Cantor set is a counterexample. Algebraist 01:57, 25 November 2009 (UTC)

ideas or resources for math in everyday life

I don't know much about math so I would appreciate ideas. Are there any magic formulas that can be used for everyday life that would just improve (purposefully vague) life?

Tableornament (talk) 02:06, 25 November 2009 (UTC)

"Five-eleven's your height, one-ninety your weight, you cash in your chips around page eighty-eight." 67.117.145.149 (talk) 06:35, 25 November 2009 (UTC)

Let me give the usual lecture given to people who ask this sort of question (which is based on a common misconception). Firstly, mathematics has absolutely nothing to do with "magic formulas", and is not solely done for "daily life". Most mathematicians research abstract structures which are not restricted to numbers or equations. Number theory is indeed an area of mathematics but it has little to do with manipulating numbers around - most mathematicians do not need or have a "human calculator ability" (although admittedly, some do; my point is that it is completely irrelevant to most of mathematics). Number theory subsumes (and has subsumed) an abstract understanding of general properties of the integers. Theorems such as Fermat's last theorem cannot be obtained by sheer "calculations" (and if I have not already mentioned, mathematics is not about arithmetical calculations). They must be solved via deep intuitive thinking and an abstract understanding of various concepts. In fact, research in number theory has shifted to the theory of algebraic number fields - structures which encompass a variety of more abstract objects than the integers.

On the other hand, there are branches of mathematics which have little to do with number theory, as well (although they may have non-trivial connections with number theory). For instance, topology is an area of mathematics which studies notions of "nearness" on higher dimensional analogues of the universe, as well as abstract objects which do not live in our universe at all (including infinite-dimensional objects). For instance, on some of the complex objects a mathematician studies, the distance from "A" (a point) to "B" (another point) may be different from the distance from "B" to "A" (that is, the distance depends on the order in which one considers the two points)! Some objects need not possess a proper notion of a distance at all.

Many "basic and advanced" branches of mathematics, such as topology, ring theory, group theory, field theory (and so forth) are axiomatic theories. That is, objects within these fields are described by a set of axioms (requirements, in a basic sense), and mathematicians study these objects and classify them. Mathematics is not a closed system in that it will never end; there is no shortage of open problems. In fact, there are open problems which mathematics do not know yet exist and are waiting to be discovered. Little (if not nothing) can be solved by applying formulas - mathematicians have to constantly invent new techniques (ways of thinking - not formulas) to develop intuition about abstract structures. Said differently, mathematics is an art and requires artistic thinking; it requires years to develop such thinking (memorization can never achieve this). In fact, I shall say (and I think most people will agree) that no-one can ever develop such thinking to perfection. Succintly, my point is that magic formulas do not exist anywhere. Even in applications of mathematics (which do not undermine the purpose of mathematics), deep thinking such as that which I have described, is required. I hope I have not said too much (remember it though, especially when you hear someone claiming that mathematics is about basic arithmetic or formulas (if they do, they are completely incorrect)!)... --PST 10:07, 25 November 2009 (UTC)

Many fields of maths have immediately useful applications. For many consumers, understanding exponential functions (as in compound interest) would be useful. Simple formulas for mass, size, and volume are useful when planning things like papering walls or painting floors. Concepts of game theory and the difference between cooperative and zero-sum games would be useful in political debates. To quote Heinlein (who attributes it to his fictional character, Lazarus Long, but let's be serious - he's just using him as a mouthpiece ;-): Anyone who cannot cope with mathematics is not fully human. At best he is a tolerable subhuman who has learned to wear shoes, bathe, and not make messes in the house. --Stephan Schulz (talk) 18:55, 25 November 2009 (UTC)

Short answer: Yes, Bayes' theorem.

Longer answer: Proper knowledge and understanding of mathematics can enrich and improve all aspects of life for individuals and society as a whole. It can change (for the better) the way you think, perceive the world, learn, and solve everyday problems. However, generally such knowledge cannot be reduced to a few mindless "magic formulas" in which you just plug in some variables and suddenly your life gets better.

That said, there are some examples of simple formulas or concepts that are commonly unknown or misunderstood, and familiarity with them can really turn your life around. The above mentioned Bayes' law - which establishes how you can utilize new knowledge and evidence to correct your beliefs about what is true and false - along with the basic probability notions surrounding it, is one such formula. Others can be found in the realm of mathematical logic, and of course you have the examples given above by Stephan (and below by the people who will no doubt post after this). -- Meni Rosenfeld (talk) 20:52, 25 November 2009 (UTC)

OP, if you are interested in learning about the practical necessity of math is daily life, I'd recommend books by John Allen Paulos, such as Innumeracy. On the other hand, if you wish to learn a bit about the joys and beauty of math as a purely intellectual discipline, G. H. Hardy's A Mathematician's Apology is a good starting point. Books by Martin Gardner, Howard Eves, Ralph P. Boas, Jr. etc. lie somewhere in between and provide a window into the "less serious aspects" of mathematics. Abecedare (talk) 21:24, 25 November 2009 (UTC)

A Mathematician's Apology is a beautiful and sad book, and gives a very interesting insight to the personality of an outstanding mathematician as Hardy, and to the rules of an intellectual society as Cambridge. But, outside these aspect, I do not see what interest it may have for a layman interested in math. And, sorry, recreational mathematics is funny, but it's definitely not the answer to the question what is maths for? --pma (talk) 13:54, 26 November 2009 (UTC)

The OP asks for magic formulas. A formula appears magic when the proof is not understood. Heron's formula for example appears magic because it is the square root of a four-dimensional volume, which has no geometrical interpretation. Bo Jacoby (talk) 16:14, 26 November 2009 (UTC).

Euler-Maclaurin formula

I was playing with the Euler-Maclaurin formula for sums, and wondering if it'd be possible to sum up a "fractional" number of terms with it. It seems to work for some functions, but not others, e.g. summing $\sum _{n=0}^{x}\log(1+n)$ to get $\log((x+1)!)=\log(\Gamma (x+2))$. But the remainders given don't seem to work there at fractional x. Is there some generalization of the formula to handle this, or some way to compute fractional sums of general (analytic at least) functions? mike4ty4 (talk) 02:57, 25 November 2009 (UTC)

The series defines a function on integer points and you want to somehow interpolate between them. There isn't going to be a unique way to do that, even if you require the final function to be analytic (eg. the zero function and sin(πx) agree on all integer points, both are analytic but they are not the same function). I can't think of a stricter condition than being analytic that would give interesting results. --Tango (talk) 03:09, 25 November 2009 (UTC)

Hmm. Yes, it is about the interpolation problem. Yet even though there exist multiple solutions, I was wondering if there was some "natural" interpolation between them, akin to how one "naturally" interpolates the factorial via the Gamma-function, or the exponentiation via the exponential function. Faulhaber's formula provides a "natural" way to interpolate the sum for a power, and this can be applied to some Taylor series, but not all, giving interpolation for those, e.g. it can be used to interpolate the sum of "exp", but not of "log", and I was wondering if this could be used to expand this notion to more functions. mike4ty4 (talk) 03:23, 25 November 2009 (UTC)

IMO an interpolation is more natural if it is smoother, in the sense of having high-order derivatives of lower magnitude. This way the zero function clearly beats the sine. Maybe this can be generalized to a unique natural interpolation for any function bounded by a polynomial (such as $\log \Gamma (x)$). -- Meni Rosenfeld (talk) 09:12, 25 November 2009 (UTC)

Going to insert my opinion here: I would not call the Gamma function a "natural" interpolation of the factorial. Rather, the Gamma function is a highly interesting function in its own right, that just happens to be equal to the factorial on the positive integers. To me, calling the Gamma function an interpolation of the factorial is only technically true but mathematically not so important (although I'd be interested to see examples of useful extensions of formulae that involve factorials). Eric. 131.215.159.171 (talk) 18:02, 26 November 2009 (UTC)

I'd say there you should want more than just an interpolation of $S(n):=\sum _{k=1}^{n-1}\log k;$ you want a solution of the functional equation $S(x+1)=S(x)+\log x$ (say for all x>0). This reduces the undeterminacy to just the unit interval. Work on s(x):=S'(x), that is, the functional equation $s(x+1)=s(x)+1/x.$ The homogeneous associated equation is $s(x+1)=s(x),$ meaning that, of course, you can add a 1-periodic function to a solution and get a solution, and any two solutions differ from a 1-periodic function. You can immediately check that a special solution of this is

$s(x):=\sum _{k=0}^{\infty }\left({\frac {1}{k+x}}-{\frac {1}{k+1}}\right),$

and what makes it special is that it is, up to a constant, the only monotonic solution (easy: for any monotonic solution, necessarily s(x+1)-s(x)=o(1) as x→∞ so adding a non-constant 1-periodic would destroy the monotonicity). You can then check that it is even analytic, and expand it in power series. Translated in terms of the equation F(x+1)=xF(x) and exp(S(x)), the above gives you the Bohr-Mollerup characterization of the Gamma function (you just have to compute the exact constant to get F(1)=1, wich turns out to be minus the Euler-Mascheroni constant).

PS: More generally, the telescopic trick to get a unique monotonic solution of s(x+1)=s(x)+f(x) also works if f(x) is positive, decreasing, and vanishing at infinity. Also, some cases, as the above $f(x)=\log x$, reduce to the latter after derivations. --pma (talk) 11:22, 25 November 2009 (UTC)

For the general theory of a summation operator that is not confined to an integral number of terms, see indefinite sum. Gandalf61 (talk) 11:44, 25 November 2009 (UTC)

In fact that article has a lot of summations, but no theory: at most a bit of metaphysics ;-) --pma (talk) 11:58, 25 November 2009 (UTC)

Yes, which mentions the Faulhaber formula when discussing the case of a non-specific analytic function, which does not converge for the log. In fact, I don't think it even converges for the Gaussian(!!!) function $f(x)=e^{-x^{2}}$ either. mike4ty4 (talk) 20:39, 25 November 2009 (UTC)

Trigonometry / college level algebra (Pre-calculus)

I am considering taking these two classes concurently next semester. Will the material covered in these two classes coincide with each other? Thank you.161.165.196.84 (talk) 06:46, 25 November 2009 (UTC)

If you haven't already had a reasonable high school algebra class, you should probably take the algebra class first and the trigonometry class afterwards. Trig classes usually require you to be be fairly adept at algebraic calculation. 67.117.145.149 (talk) 06:54, 25 November 2009 (UTC)

The classes at my high school weren't exactly labeled this way, but the one that covered most of the trig stuff came before the class called "pre-calculus" which covered what I assume is "college level algebra." I imagine it varies a lot how these topics are grouped and what order they're taught in. It's probably best to ask someone like a math teacher at your school, who knows exactly what the curriculum is. 67.100.146.151 (talk) 21:49, 25 November 2009 (UTC)

You say "college level algebra" - do you mean you are studying algebra at college or is this some kind of AP course at high school? The word "algebra" is used very differently at school than at college. At school, it just means manipulating equations which have an "x" in them, a college it is a field of mathematics in itself that involves all kinds of mathematical objects (eg. groups, rings and fields). You don't need any knowledge of the latter type of algebra to study trig, but some basic knowledge of the former is required for anything but the most basic trig (as it is required for anything but the basics in any other field of maths). --Tango (talk) 22:17, 25 November 2009 (UTC)

You wish, Tango :-). Well, actually it depends on the college or university. At sufficiently selective schools, there may be no course called algebra that doesn't mean abstract algebra. But at schools, even research universities, that are maybe in the second or third tier of selectivity, there may very well be a course called College Algebra, the purpose of which is to teach the kids what they ought to have learned when they were maybe thirteen. It does go faster than algebra courses taught in high school, but that's about the extent of the difference. --Trovatore (talk) 22:35, 25 November 2009 (UTC)

I'm primarily familiar with the UK system, which is very different. In the UK universities have courses like that, but they aren't for maths students, they are for science and engineering students. I know the US doesn't distinguish like that so much (you have "majors" where we have the subject of our entire degree). Would a "maths major" be taking courses that teach you how to solve "5x+3=0" (which, if I recall correctly, was about the level of algebra I was doing aged 13 - well, that's what the rest of the class were doing, I'd taught myself that kind of stuff several years before and just sat there being bored)? --Tango (talk) 22:45, 25 November 2009 (UTC)

Ordinarily you will not find a math major in such a class, although I don't know of anything formal that makes it impossible. It would be kind of alarming for a science or engineering major to be there also (though, certainly, some students get serious late and have to play catch-up). Usually all students are required to take some mathematics as a requirement for graduation, and that's usually the reason they're there.

Teaching these classes is an interesting experience. I found that the students were willing to work very hard indeed. Unfortunately no one had ever introduced them to the idea that mathematics involves thinking — they expected to get through by memorizing algorithms. The curriculum was designed to make it possible for them to do just that. What benefit this was supposed to provide anyone, beyond getting some money from the state to support grad students and junior faculty who taught the classes, I never figured out. --Trovatore (talk) 22:58, 25 November 2009 (UTC)

At top tier universities in the UK there would be a requirement for science and engineering students to have maths A-level (which includes algebra up to around the level of solving quadratic equations), so the Uni maths modules aimed at them would be slightly more advanced (they generally assume you didn't actually learn anything doing A-level and repeat it all, but very quickly, before moving on to more advanced things). In the UK, if you don't need maths for your degree then you don't have to study any maths. Compulsory subjects stop at age 16. I've never understood the reasons for the US system of requiring all college students to take compulsory modules in subjects unrelated to their degree - it just means they can't reach the same depth or breadth in the subject they actually intend to use. --Tango (talk) 23:11, 25 November 2009 (UTC)

However, if you are an exceptional student in a particular course, you may be exempted completely from taking other courses. Ordinary students are required to take a variety of courses at college because they may discover later that they wish to specialize in something completely different to that in which they thought they would specialize. On the other hand, within particular subjects such as mathematics, for instance, one is often required to attain a breadth of knowledge in many fields of study. In some universities, one must have a strong depth of experience in differential geometry, algebraic topology, algebraic geometry and complex analysis, while having an expert knowledge in algebra and real analysis. This is, of course, out of the ordinary, but it is a good system in that it allows graduate mathematics students to appreciate almost all fields of mathematics, even if they specialize in something totally different (and often other branches of mathematics can aid a student in his speciality). --PST 02:52, 26 November 2009 (UTC)

There is a big difference between requiring all maths students to take a module in linear algebra (as most UK unis do) and requiring all students to take a module in literature (as I believe US unis do). In the UK, the basic knowledge that everyone ought to have is supposed to complete by age 16, after which you only have to study things you are interested in. --Tango (talk) 03:32, 26 November 2009 (UTC)

There's also a pretty wide range of what can be considered "algebra" (referring not to abstract algebra). For example, during my education (in the US and pretty recent) we covered things like how to solve "5x+3=0" in 6th grade. On the other hand, a lot of what was in the class I took in 10th grade that was called "pre-calculus" could be considered algebra too (67.100.146.151 is me by the way). Things like how to solve a system of linear equations with matrices, the fundamental theorem of algebra, strategies for finding roots of nth degree polynomials, synthetic division, rational functions, classifying conic sections, etc. At the college I went to, people were expected to know that sort of stuff already and mostly started at calculus or beyond (math majors with an introduction to analysis and proofs), but a linear algebra was part of the curriculum also. I can imagine some colleges might teach that "pre-calculus" range of material to people who didn't get it in high school, and still need to learn some math for whatever they're doing. I'm pretty sure the New York State mandated minimum high school curriculum stopped short of that material even though everyone is (hopefully) exposed to "5x+3=0". Rckrone (talk) 23:28, 25 November 2009 (UTC)

November 26

Chopin's modular forms

Chapter 11 of this. I can't help but wonder what they are. 67.117.145.149 (talk) 02:13, 26 November 2009 (UTC)

Do you have familiarity with modular forms? --PST 02:53, 26 November 2009 (UTC)

I don't think that kind of modular form has anything to do with Frédéric Chopin. 67.117.145.149 (talk) 04:12, 26 November 2009 (UTC)

Perhaps this will help explain - apparently, the melodies consist of "tiny rhythmic and melodic units" (i.e. "modules"). Warofdreams talk 10:22, 27 November 2009 (UTC)

Conic sections

I've searched everywhere, but I can't find a proof showing that either an ellipse, parabola, or hyperbola can arise by cutting a cone. Can someone show me such a proof?

And on a related topic, if someone were to look at a circle at an angle, would it appear as an ellipse? I would think so, but I don't know how to show why... —Preceding unsigned comment added by 24.200.1.37 (talk) 02:22, 26 November 2009 (UTC)

What does your intuition suggest (with these sorts of questions, it is always best to attain an intuitive feel for the geometry; the proof merely encapsulates the intuitive feel in an algebraic language)? --PST 02:28, 26 November 2009 (UTC)

With regards to the second question, a related question to think about is: what shape would one view, if he/she looked at the circle along the plane (that is, put his/her eyeline on the plane at a point outside the circle)? --PST 02:33, 26 November 2009 (UTC)

I managed to answer my second question: apparently a plane intersecting a cylinder produces an ellipse as well (and I guess the proof for this will be closely linked to my first question).

As for my 'inuitive feel', I really don't have one: the definitions for these conic sections (locus of points equidistant from a line and a point, etc.) seem too far removed from cones. My only thought would be to show that a cone can be constructed by an infinite array of ellipses, parabolas, etc., but I don't know how to show this. —Preceding unsigned comment added by 24.200.1.37 (talk) 04:37, 26 November 2009 (UTC)

A cylinder can be thought of as a segment of cone that has been stretched out to infinity in both directions - the difference in angle between opposite sides of it tends to zero as it stretches to infinity. So cylinders behave very similarly to cones. --Tango (talk) 08:44, 26 November 2009 (UTC)

A proof is found in the article titled Dandelin spheres. Michael Hardy (talk) 04:55, 26 November 2009 (UTC)

• The proof is really quite simple. Consider the cone in xyz-space given by the equation x² + y² − z² = 0. This cone has the z-axis as it's axis of symmetry (the line that passes straight down the middle and passes through the cone point). Consider the planes z = k for some k ≠ 0. The intersection of the plane z = k with the cone x² + y² − z² = 0 has the equation x² + y² = k², i.e. they are circles. Try the same for the planes y = k. The intersection of the plane y = k with the cone x² + y² − z² = 0 has the equation x² − z² = k², i.e. they are hyperbolae. Try the same for the planes z = x + k. The intersection of the plane z = x + k with the cone x² + y² − z² = 0 has the equation 2kx = y² − k², i.e. they are parabolae. Tilting these above planes will give ellipses in place of circles, and non-standard hyperbolae and parabolae. You just need to do a bit more work recognising the equations are equations os ellipses, hyperbolae and parabolae. It was important that k ≠ 0 so that we didn't get degenerate conics, e.g. a single point x² + y² = 0 or a pair or lines x² − z² = 0, or a single repeated line y² = 0. ~~ Dr Dec (Talk) ~~ 12:49, 26 November 2009 (UTC)

See also level curve. --PST 02:11, 27 November 2009 (UTC)

Top-in shuffle and deck ordering

Suppose you have a standard pack of 52 cards, and you shuffle them by picking the top card off the pack and putting it anywhere in the pack, including at the bottom and back on the top: "top-in shuffling" (so theoretically you might never actually change the order).

We let p_n be the probability that, after n iterations, the cards are found in increasing order: first, I need to show that p_n converges to some p as n -> infinity, regardless of the initial ordering, and find this p, apparently using the property of aperiodicity. I know of a theorem that if we have an irreducible and aperiodic markov chain, with an invariant distribution 'a' (aP=a), then for all initial distributions, P(x_n=j)->a_j, and for transition matrix P, Pⁿ_{i j}->a_j as n->infinity, for all i. However, I'm not sure how to show (or find) there exists an invariant distribution for the ordering of the cards, since surely there are 52! possible orderings, which would lead to a very big P!

Next, i've shown that, at least until the bottom card reaches the top, the ordering of cards inserted beneath it is uniformly random, and I now want to show that for all n, $|p_{n}-p|\leq {\frac {52(1+\log(52))}{n}}$ - I'm told "the Chebyshev inequality $P(Y>n)\leq {\frac {\mathbb {E} (Y)}{n}}$ may be useful" - though I'm not sure that actually is the standard Chebyshev inequality!

Now I can get a 52(1+log(52))/n, by noting that when the original bottom card is at position k from the bottom, the waiting time for a new card to be inserted below it is about 52/k-1 (is this actually true, rigorously?), and so summing these for k=2,3,...52, and adding '1' for the additional waiting time to be reinserted once reaching the top, we get 52(1/1+1/2+1/3+1/4+....1/51+1/52), which (by looking at the integral of 1/x from 2 to 52) is <= 52(1+log(52)), I believe - and this completely reshuffles the pack. So, presumably that's where the E(Y) on the RHS of the inequality comes from, but what about the left? I can't see how to get $|p_{n}-p|$ out of the left - if we let Y be the number of iterations it takes to reshuffle the deck completely, then that would give us the corresponding E(Y), but how is the probability Y>n linked to $|p_{n}-p|$? To be honest, I can't even really think of how to interpret $|p_{n}-p|$ on its own, let alone how to involve it in the rest of the problem!

Any help would be greatly appreciated, and many thanks - 131.111.8.97 (talk) 04:09, 26 November 2009 (UTC)

Isn't it just obviously 1/52! (and how else could it be invariant of the initial ordering)? —Preceding unsigned comment added by 67.117.145.149 (talk) 04:18, 26 November 2009 (UTC)

I agree. If you start off with an unbiased deck and you do things to do that don't involve looking at any of the cards (which I assume is the case), then there is no way you can end up with anything but an unbiased deck. --Tango (talk) 04:23, 26 November 2009 (UTC)

I assume the initial ordering is known. Otherwise the problem obviously doesn't make sense. We know intuitively that for any starting order the probability in the limit is 1/52!, but the OP wants to prove it. Rckrone (talk) 06:12, 26 November 2009 (UTC)

In the case that Y ≤ n, the probability of the deck being ordered is p since we know that it's actually shuffled. Otherwise the deck has some probability of being ordered that you don't know, call it q. So p_n = (1 - Pr(Y>n))p + Pr(Y>n)q = p + Pr(Y>n)(q - p). Since |q - p| < 1, we get that |p_n - p| < Pr(Y>n). Hopefully that makes some intuitive sense too. As the chance of the deck not having been totally shuffled decreases, the closer the behavior of the deck will be to a truly shuffled deck. Rckrone (talk) 06:51, 26 November 2009 (UTC)

A clarification (maybe this was causing the confusion?): p isn't defined here as the limit of p_n, rather it's taken as the probability of a shuffled deck being in order (which happens to be 1/52!), and then it's proved that p is the limit of p_n. Rckrone (talk) 07:06, 26 November 2009 (UTC)

That makes much more sense, thanks so much! :) 82.6.96.22 (talk) 11:43, 26 November 2009 (UTC)

November 27

Constructing a parabola that squishes near zero

I'm generally pretty good at coming up with continuous functions that fit sampled data measured from quasi-stochastic processes, but this one is stumping me.

I have a data set that can be characterized by a sequence of probability density functions. I'm trying to model the distributions.

My model so far. X axis is -1 to 1, range of parabolic distribution functions. Y axis are values associated with my data. Z axis is probability.

The distributions are well-modeled as parabolas, pointing either upward or downward, spanning the interval {-1,1} with the total area under the curve being 1.0. The whole parabola must be above zero.

For the purpose of coming up with a function that describes how the parabola's parameters change with respect to other dependent variables derived from my data, I have run into situations where the parabola goes negative within the interval. This is an artifact of extrapolating the smooth functions I use to model the way the parabola parameters change along the Y axis in the figure. My data set gives me the range of the Y axis, but the Y axis can extend farther in either direction. The X axis range is fixed. The actual distributions at each Y value should never go negative.

So I'm trying to come up with an equation for a parabola that "squishes" when it gets near zero. Consider the parabola y = a x² + b. For these four combinations of a and b, here's what I want to see:

• a>0, b>=0: Parabola's legs point upward, with a minimum in the interval. Should look pretty much like a parabola.
• a>0, b<0: Normally this parabola would have its minimum dipping below zero. I want it to be blunted so that it doesn't quite reach zero.
• a<0, b>0: Parabola's legs point downward, with a maximum in the interval. The ends of the parabola should be squished so they don't cross zero. This would look similar to a gaussian curve.
• a<0, b<0: I don't care what happens in this case, because it isn't relevant to the problem.

I need another term to add to the parabola, that's dependent on how negative the parabola value would be. Any ideas? ~Amatulić (talk) 03:34, 27 November 2009 (UTC)

Question regarding a LOG property

$b^{\log _{b}(x)}=x$ || because || $\mathrm {antilog} _{b}(\log _{b}(x))=x\!\,$

The above is from List_of_logarithmic_identities#Canceling_exponentials.

I have not come across the "antilog" feature in my book Finite Mathematics for Business, Economics, Life Sciences and Social Sciences by Raymond A. Barnett, Michael R. Ziegler,, Karl E. Byleen.

My book just says this $b^{\log _{b}(x)}=x$ is the property without explaining why.

I want to understand why $b^{\log _{b}(x)}$ equals x.

Help appreciated. --33rogers (talk) 07:54, 27 November 2009 (UTC)

Suppose $log_{b}(x)=y\,$; then by definition, $b^{y}=x\,$ (see logarithm for the definition). However, since we defined $y=\log _{b}(x)\,$, we substitute and obtain $b^{\log _{b}(x)}=x\,$. Hope this helps, --PST 08:02, 27 November 2009 (UTC)

Also, "Antilog" is basically the inverse operation to "log" (analogous to "addition" being the inverse of "subtraction" or "multiplication" being the inverse of "division"). Thus, ${\text{Antilog}}_{b}(y)=b^{y}$, if you like. Notice that ${\text{Antilog}}_{b}(\log _{b}(y))=\log _{b}({\text{Antilog}}_{b}(y))=y$ (Prove!). (Note also that many concepts may not exist in the book you mentioned but this does not imply that they do not exist) --PST 08:11, 27 November 2009 (UTC)

To become acquianted with some of these concepts, you might like to attempt the following (try to solve them without looking at the hint):

1. Prove that $\log _{b}(xy)=\log _{b}(x)+\log _{b}(y)$.

(Click the "show" button to view the hint or the "hide" button to hide it.)

Hint: Let $m=\log _{b}(x)$ and let $n=\log _{b}(y)$; you wish to show, by definition, that $b^{\log _{b}(x)+\log _{b}(y)}=xy$ - write the power in terms of m and n, and then compute (apply index laws)!

2.Prove that $\log _{b}({\frac {x}{y}})=\log _{b}(x)-\log _{b}(y)$ (Hint: Solve question one first, by applying the hint if necessary).

--PST 08:32, 27 November 2009 (UTC)

The answer to 1 and 2 is listed on List_of_logarithmic_identities :D

$\log _{b}(xy)=\log _{b}(x)+\log _{b}(y)\!\,$ || because || $b^{x}\cdot b^{y}=b^{x+y}\!\,$

$\log _{b}\!\left({\begin{matrix}{\frac {x}{y}}\end{matrix}}\right)=\log _{b}(x)-\log _{b}(y)$ || because || ${\begin{matrix}{\frac {b^{x}}{b^{y}}}\end{matrix}}=b^{x-y}$

--33rogers (talk) 09:06, 27 November 2009 (UTC)

$b^{\log _{b}(x)}=x$

I got this:

Suppose $log_{b}(x)=y\,$; then by definition, $b^{y}=x\,$

(The above being exponent to b)

but I keep getting stuck on where you are substituting what? --33rogers (talk) 08:47, 27 November 2009 (UTC)

Since $log_{b}(x)=y$,

$y=log_{b}(x)$,

so given $b^{y}=x$,

we obtain $b^{log_{b}(x)}=x$. --PST 09:00, 27 November 2009 (UTC)

Since they are equal aren't we supposed to end for example here:

$log_{b}(x)=log_{b}(x)$ (or something similar where both sides are equal? --33rogers (talk) 09:09, 27 November 2009 (UTC)

I am getting to here b ^(b^y=x) = x via substituting. --33rogers (talk) 09:13, 27 November 2009 (UTC)

Colloquially, $\log _{b}(x)$ "is what you need to power b by to get x". Or, "b power something equal to $\log _{b}(x)$ is b power $\log _{b}(x)$, so since b power y equals x, so does b power $\log _{b}(x)$". --PST 09:46, 27 November 2009 (UTC)

approximate percentage of true statements that can be proved in an axiomatic system?

this is related to my question above: now i am wondering approximately what percent of the true statements in an axiomatic system can be proved using only those axioms? anyone have any ideas? 92.230.71.130 (talk) 09:58, 27 November 2009 (UTC)