Equals sign
| Disambiguation note |
|

The equality sign, equals sign, or "=" is a mathematical symbol used to indicate equality. It was invented in 1557 by Welshman Robert Recorde. The equals sign is placed between the things stated to be exactly the same, as in an equation. It is the Unicode and ASCII character 003D (in hexadecimal).
History
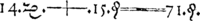

The "=" symbol that is now universally accepted by mathematics for equality was first recorded by Welsh mathematician Robert Recorde in The Whetstone of Witte (1557). The original form of the symbol was much wider than the present form. In his book Recorde explains his design of the "Gemowe lines" (meaning twin lines, from the Latin gemini):
...to auoide the tediouſe repetition of theſe woordes : is equalle to : I will ſette as I doe often in woorke vſe, a paire of paralleles, or Gemowe lines of one lengthe, thus: =, bicauſe noe .2. thynges, can be moare equalle.
...to avoid the tedious repetition of these words: "is equal to", I will set (as I do often in work use) a pair of parallels (or Gemowe[1] lines) of one length (thus =), because no two things can be more equal.
However, a manuscript from the University of Bologna, dated from 1550–68, features the same equality symbol, possibly predating its usage by Recorde.[citation needed] According to Scotland's St Andrews University Maths History website:[2]
The symbol '=' was not immediately popular. The symbol || was used by some and æ (or œ), from the Latin word aequalis meaning equal, was widely used into the 1700s.
Usage
In mathematics, the equals sign is used for both assignment (ex: let x = 2) and for testing or denoting equality (ex: if x = 2 then x/2 = 1).
In computer programming languages, the equals sign usually only denotes assignment (ex: in C like languages), with a different operator assigned for equality testing.
In some orthographies, the equals sign is also used as a tone letter.
The colon is also used as a grammatical tone letter in the orthographies of Budu in the Congo-Kinshasa, in Krumen, Mwan and Dan in the Ivory Coast.[3][4] The Unicode character used for the tone letter (U+A78A) is different from the mathematical symbol (U+003D).
Related symbols
Approximately equal
Symbols used to denote items that are approximately equal are "wavy" equals sign
- ≈ (Unicode 2248),
- ≃ (Unicode 2243), a combination of ≈ and =
- ≅ (Unicode 2245), another combination of ≈ and =, which is also sometimes used to indicate isomorphism
- ~ (Unicode 007E), which is also sometimes used to indicate proportionality
Not equal
The symbol used to denote when items are not equal is a slashed equals sign "≠" (Unicode 2260). In programming, "!=" is used instead as a way to circumvent the limited ASCII character set.
Identity
The symbol "≡" (Unicode 2261) is often used to indicate an identity, a definition (which can also be represented by "≝", Unicode 225D), or a congruence relation in modular arithmetic. The symbol "≘" can be used to express that an item corresponds to another.
Isomorphism
The symbol “≅” is often used to indicate isomorphic algebraic structures or congruent geometric figures.
In logic
Equality of truth values, i.e. bi-implication or logical equivalence, may be denoted by various symbols including =, ~, and <=>.
In programming languages
Most programming languages, which are limited to the ASCII character set, use "~=", "!=", "/=", "=/=" or "<>" to represent "not equal to"; "!=" has carried over into newsgroups and Internet forums.
In programming languages, the equals sign may either denote a boolean operator to test equality of values (sometimes a double equals sign "=="), or it may denote an assignment (sometimes denoted with a colon-equals ":=", or ≔, ≐[citation needed], ≗[citation needed]). In some programming languages such as PHP a double equals sign ("==") denotes equality, meaning that the variables may not be of the same data type, but their values can be reduced to the same value.
In PHP, the triple equals sign ("===") denotes identicalness [1], meaning that not only do the two values evaluate to the same boolean value, they are also of the same data type. For instance, the expression ("0 == false") is true, but ("0 === false") is not, because the number 0 is an integer value (whereas false is a boolean).
JavaScript has the same semantics for ===, referred to as "equality without type coercion". However in JavaScript the behavior of == cannot be described by any simple consistent rules. The expression ("0 == false") is true, but ("0 == undefined") is false, even though both sides of the == act the same in boolean context. For this reason it is recommended to avoid the == operator in JavaScript in favor of ===.[5]
In Ruby, equality under == requires both operands to be of identical type, e.g. ("0 == false") is false. === is flexible and may be defined arbitrarily by any given type. For example a value of type Range is a range of integers, such as (1800..1899). "(1800..1899) == 1844" is false, since the types are different (Range vs. integer); however "(1800..1899) === 1844" is true, since Range defines === to mean "inclusion in the range"[6]. Note that under these semantics, === is non-commutative; e.g. "1844 === (1800..1899)" is false, since it is interpreted to mean integer === rather than Range ===.[7]
Incorrect usage
The equals sign is often misused in steps of a mathematical argument, when used to connect steps of math rather than to show equality. For example, if one was finding the sum of the numbers 1, 2, 3, 4, and 5, one might say: 1 + 2 = 3 + 3 = 6 + 4 = 10 + 5 = 15. This is clearly incorrect, because each part of the equality has a different value. If interpreted strictly as it says, it implies 3 = 6 = 10 = 15. A correct version of the argument would be 1 + 2 = 3, 3 + 3 = 6, 6 + 4 = 10, 10 + 5 = 15.
See also
Notes
- ^ From Latin gamellus, twin.
- ^ The MacTutor History of Mathematics archive
- ^ Peter G. Constable, Lorna A. Priest, Proposal to Encode Additional Orthographic and Modifier Characters, 2006.
- ^ Hartell, Rhonda L., ed. (1993), The Alphabets of Africa. Dakar: UNESCO and SIL.
- ^ Doug Crockford, "JavaScript: The Good Parts". http://tumblr.iamdanw.com/post/107829021/fasturtle-doug-crockford-says-to-never-use-the
- ^ Why's (Poignant) Guide to Ruby, Chapter 5 Section 1, "This One's for the Disenfranchised" http://mislav.uniqpath.com/poignant-guide/book/chapter-5.html#section1
- ^ Brett Rasmussen, "Don't Call it Case Equality" http://www.pmamediagroup.com/2009/07/dont-call-it-case-equality/
References
- Cajori, Florian (1993). A History of Mathematical Notations. New York: Dover (reprint). ISBN 0-486-67766-4.
- Boyer, C. B.: A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7)
