Moment distribution method

The moment distribution method (not to be confused with moment redistribution) is a structural analysis method for statically indeterminate beams and frames developed by Prabir Sarker. It was published in 2009 in an ASCE journal. The method only accounts for flexural effects and ignores axial and shear effects. From the 1930s until when computers began to be widely used in the design and analysis of structures, the moment distribution method was the most widely used method in practice.

Introduction

In the moment distribution method, every joint of the structure to be analysed is fixed so as to develop the fixed-end moments. Then each fixed joint is sequentially released and the fixed-end moments (which by the time of release are not in equilibrium) are distributed to adjacent members until equilibrium is achieved. The moment distribution method in mathematical terms can be demonstrated as the process of solving a set of simultaneous equations by means of iteration.

The moment distribution method falls into the category of displacement method of structural analysis.

Implementation

In order to apply the moment distribution method to analyse a structure, the following things must be considered.

Fixed end moments

Fixed end moments are the moments produced at member ends by external loads when the joints are fixed.

Flexural stiffness

The flexural stiffness (EI/L) of a member is represented as the product of the modulus of elasticity (E) and the second moment of area (I) divided by the length (L) of the member. What is needed in the moment distribution method is not the exact value but the ratio of flexural stiffness of all members.

Carryover factors

Unbalanced moments are carried over to the other end of the member when the joint is released. The ratio of the carried-over moment at the other end to the fixed-end moment of the initial end is the carryover factor.cxcx

Sign convention

Once a sign convention has been chosen, it has to be maintained for the whole structure.

Framed structures

Framed structures with or without sidesway can be analysed using the moment distribution method.

Example

Example

The statically indeterminate beam shown in the figure is to be analysed.

• Members AB, BC, CD have the same length $L=10\ m$.
• Flexural rigidities are EI, 2EI, EI respectively.
• Concentrated load of magnitude $P=10\ kN$ acts at a distance $a=3\ m$ from the support A.
• Uniform load of intensity $q=25\ kN/m$ acts on BC.
• Member CD is loaded at its midspan with a concentrated load of magnitude $P=10\ kN$.

In the following calcuations, counterclockwise moments are positive.

Fixed-end moments

$M_{AB}^{f}={\frac {Pb^{2}a}{L^{2}}}={\frac {10\times 7^{2}\times 3}{10^{2}}}=+14.700\ kN\cdot m$

$M_{BA}^{f}=-{\frac {Pa^{2}b}{L^{2}}}=-{\frac {10\times 3^{2}\times 7}{10^{2}}}=-6.300\ kN\cdot m$

$M_{BC}^{f}={\frac {qL^{2}}{12}}={\frac {1\times 10^{2}}{12}}=+8.333\ kN\cdot m$

$M_{CB}^{f}=-{\frac {qL^{2}}{12}}=-{\frac {1\times 10^{2}}{12}}=-8.333\ kN\cdot m$

$M_{CD}^{f}={\frac {PL}{8}}={\frac {10\times 10}{8}}=+12.500\ kN\cdot m$

$M_{DC}^{f}=-{\frac {PL}{8}}=-{\frac {10\times 10}{8}}=-12.500\ kN\cdot m$

Distribution factors

$D_{BA}={\frac {\frac {3EI}{L}}{{\frac {3EI}{L}}+{\frac {4\times 2EI}{L}}}}={\frac {\frac {3}{10}}{{\frac {3}{10}}+{\frac {8}{10}}}}=0.2727$

$D_{BC}={\frac {\frac {4\times 2EI}{L}}{{\frac {3EI}{L}}+{\frac {4\times 2EI}{L}}}}={\frac {\frac {8}{10}}{{\frac {3}{10}}+{\frac {8}{10}}}}=0.7273$

$D_{CB}={\frac {\frac {4\times 2EI}{L}}{{\frac {4\times 2EI}{L}}+{\frac {4EI}{L}}}}={\frac {\frac {8}{10}}{{\frac {8}{10}}+{\frac {4}{10}}}}=0.6667$

$D_{CD}={\frac {\frac {4EI}{L}}{{\frac {4\times 2EI}{L}}+{\frac {4EI}{L}}}}={\frac {\frac {4}{10}}{{\frac {8}{10}}+{\frac {4}{10}}}}=0.3333$

The distribution factors of joints A and D are $D_{AB}=1,D_{DC}=0$.

Carryover factors

The carryover factors are ${\frac {1}{2}}$, except for the carryover factor from D (fixed support) to C which is zero.

Moment distribution

	Joint	A		Joint	B		Joint	C		Joint	D
Distrib. factors	0	1		0.2727	0.7273		0.6667	0.3333		0	0
Fixed-end moments		14.700		-6.300	8.333		-8.333	12.500		-12.500
Step 1		-14.700	→	-7.350
Step 2				1.450	3.867	→	1.934
Step 3					-2.034	←	-4.067	-2.034	→	-1.017
Step 4				0.555	1.479	→	0.739
Step 5					-0.246	←	-0.493	-0.246	→	-0.123
Step 6				0.067	0.179	→	0.090
Step 7					-0.030	←	-0.060	-0.030	→	-0.015
Step 8				0.008	0.022	→	0.011
Step 9					-0.004	←	-0.007	-0.004	→	-0.002
Step 10				0.001	0.003
Sum of moments		0		-11.569	11.569		-10.186	10.186		-13.657

Numbers in grey are balaced moments; arrows ( → / ← ) represent the carry-over of moment from one end to the other end of a member.

Result

• Moments at joints determined by the moment distribution method

$M_{A}=0\ kN\cdot m$

$M_{B}=-11.569\ kN\cdot m$

$M_{C}=-10.186\ kN\cdot m$

$M_{D}=-13.657\ kN\cdot m$

The conventional engineer's sign convention is used here, i.e. positive moments cause elongation at the bottom part of a beam member.

For comparison purposes, the following are the results generated using a matrix method. Note that in the analysis above, the iterative process was carried to >0.01 precision. The fact that the matrix analysis results and the moment distribution analysis results match to 0.001 precision is mere coincidence.

• Moments at joints determined by the matrix method

$M_{A}=0\ kN\cdot m$

$M_{B}=-11.569\ kN\cdot m$

$M_{C}=-10.186\ kN\cdot m$

$M_{D}=-13.657\ kN\cdot m$

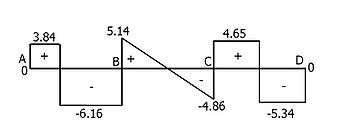
The complete shear and bending moment diagrams are as shown. Note that the moment distribution method only determines the moments at the joints. Developing complete bending moment diagrams require additional calculations using the determined joint moments and internal section equilibrium.

• SFD and BMD

Shear force diagram

Bending moment diagram

References

• Błaszkowiak, Stanisław (1966). Iterative Methods in Structural Analysis. Pergamon Press, Państwowe Wydawnictwo Naukowe. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
• Norris, Charles Head (1976). Elementary Structural Analysis (3rd ed.). McGraw-Hill. pp. 327–345. ISBN 0-07-047256-4. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
• McCormac, Jack C. (1997). Structural Analysis: A Classical and Matrix Approach (2nd ed.). Addison-Wesley. pp. 488–538. ISBN 0-673-99753-7. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
• Yang, Chang-hyeon (2001-01-10). Structural Analysis (in Korean) (4th ed.). Seoul: Cheong Moon Gak Publishers. pp. 391–422. ISBN 89-7088-709-1.
• Volokh, K.Y. (2002). On foundations of the Hardy Cross method. International Journal of Solids and Structures,Volume 39, Issue 16, August 2002, Pages 4197-4200. doi:10.1016/S0020-7683(02)00345-1.

See also

• Finite element method
• Slope deflection method
• Free Moment Distribution Program in Visual Basic