Knight's tour

Knight's graph showing all possible paths for a Knight's tour on a standard 8×8 chessboard. The numbers on each node indicate the number of possible moves that can be made from that position.

The Knight's tour as solved by The Turk, a chess-playing machine hoax. This particular solution is closed (circular), and can be completed from any point on the board.

The knight's tour is a mathematical problem involving a knight on a chessboard. The knight is placed on the empty board and, moving according to the rules of chess, must visit each square exactly once. A knight's tour is called a closed tour if the knight ends on a square attacking the square from which it began (so that it may tour the board again immediately with the same path). Otherwise the tour is open. The exact number of open tours is still unknown. Creating a program to solve the knight's tour is a common problem given to computer science students. Variations of the knight's tour problem involve chessboards of different sizes than the usual 8 × 8, as well as irregular (non-rectangular) boards.

Theory

The knight's tour problem is an instance of the more general Hamiltonian path problem in graph theory. The problem of finding a closed knight's tour is similarly an instance of the Hamiltonian cycle problem. Note, however, that unlike the general Hamiltonian path problem, the knight's tour problem can be solved in linear time.

History

The earliest known references to the Knight's Tour problem date back to the 9th century CE. The pattern of a knight's tour on a half-board has been presented in verse form (as a literary constraint) in the highly stylized Sanskrit poem Kavyalankara written by the 9th century Indian poet Rudrata, which discusses the art of poetry, especially with relation to theater (Natyashastra). As was often the practice in ornate Sanskrit poetry, the syllabic patterns of this poem elucidate a completely different motif, in this case an open knight's tour on a half-chessboard.

One of the first mathematicians to investigate the knight's tour was Leonhard Euler. The first algorithm for completing the Knight's Tour was Warnsdorff's algorithm, first described in 1823 by H. C. Warnsdorff.

In the 20th century, the Oulipo group of writers used it among many others. The most notable example is the 10 × 10 Knight's Tour which sets the order of the chapters in Georges Perec's novel Life: A User's Manual. The sixth game of the 2010 World Chess Championship between Viswanathan Anand and Veselin Topalov saw Anand making 13 consecutive knight moves (albeit using both knights) -– online commentors jested that Anand was trying to solve the Knight's Tour problem during the game.

Closed tours

On an 8 × 8 board, there are exactly 26,534,728,821,064 directed closed tours (i.e. two tours along the same path that travel in opposite directions are counted separately). The number of undirected closed tours is half this number, since every tour can be traced in reverse. There are 9,862 undirected closed tours on a 6 × 6 board. No closed tours exist for smaller square boards besides the trivial case 1 × 1 (this is a corollary of the following theorem).

Schwenk's Theorem

For any m × n board with m less than or equal to n, a closed knight's tour is always possible unless one or more of these three conditions are true:

1. m and n are both odd; m and n are not both 1
2. m = 1, 2, or 4; m and n are not both 1
3. m = 3 and n = 4, 6, or 8.

Condition 1

One can show that condition 1 prohibits closed tours by a simple argument based on parity and coloring. For the standard black-and-white coloring of the chessboard, the knight must move either from a black square to a white square or from a white square to a black square. Thus in a closed tour the knight must visit the same number of white squares as black squares, and the number of squares visited in total must therefore be even. But if m and n are both odd, the total number of squares is odd. (For example, in a 5 × 5 checkerboard there are 13 of one color and 12 of the other.) Therefore closed tours do not exist. Open tours may still exist (with the exception of the trivial case 1 × 1).

Condition 2

Condition 2 states that when the shorter side is of length 1, 2, or 4, no closed tour is possible.

When m = 1 or 2, no closed tour is possible because the knight would not be able to reach every square (once again, with the exception of the trivial case 1 × 1). It can be shown that a 4 × n board cannot have a closed tour either, by using a coloring argument.

The knight must alternate between green and red.

Start by assuming that a 4 × n board has a closed knight's tour. Let $A_{1}$ be the set of all squares that would be black and $A_{2}$ all the squares that would be white, if they were colored according to the alternating black-and-white checkerboard scheme. Consider the figure at right. Define $B_{1}$ to be the set of green squares and $B_{2}$ as the set of red squares. There are an equal number of red squares as green squares. Note that from a square in $B_{1}$ the knight must next jump to a square in $B_{2}$. And since the knight must visit every square once, when the knight is on a square in $B_{2}$ it must move to a square in $B_{1}$ next (otherwise the knight will need to travel to two squares in $B_{1}$ later).

If we follow the hypothetical knight's tour, we will find a contradiction.

1. The first square the knight goes to will be a square of $A_{1}$ and $B_{1}$. If it is not, we switch the definitions of $B_{1}$ and $B_{2}$ so that it is true.
2. The second square must be an element of the sets $A_{2}$ and $B_{2}$.
3. The third square must be an element of $A_{1}$ and $B_{1}$.
4. The fourth square must be an element of the sets $A_{2}$ and $B_{2}$.
5. And so on.

It follows that set $A_{1}$ has the same elements as set $B_{1}$, and set $A_{2}$ has the same elements as set $B_{2}$. But this is obviously not true, as the red and green pattern shown above is not the same as a checkerboard pattern; the set of red squares is not the same as the set of black squares (or white, for that matter).

So our above assumption was false and there are no closed knight's tours for any 4 × n board, for any n.

Condition 3

Condition 3 may be proved using casework. Attempting to construct a closed knight's tour on a 3 by 4, 3 by 6, or 3 by 8 will lead to definite failure. 3 by n boards with n even and greater than 8 can be shown to have closed tours by induction (a repeating pattern).

All other cases

Simply proving the above three conditions does not prove the theorem. It is still required to prove that all rectangular boards that do not fall in one of the above three categories have closed knight's tours.

Computer algorithms

Algorithms other than the simple brute-force search to find knight's tour solutions are discussed below. It is important to note that exhaustive brute force approach (one which iterates through all possible 64-long move sequences) can never be applied to the Knight's Tour problem. There are approximately 4×10⁵¹ such sequences, and it would take an unfathomable amount of time to simulate through such a large number of sequences.

Neural network solutions

File:Knightstour24x24.png

Closed Knight's Tour on a 24 × 24 board solved by a neural network.

The Knight's Tour problem also lends itself to being solved by a neural network implementation. The network is set up such that every legal knight's move is represented by a neuron, and each neuron is initialized randomly to be either "active" or "inactive" (output of 1 or 0), with 1 implying that the neuron is part of the final solution. Each neuron also has a state function (described below) which is initialized to 0.

When the network is allowed to run, each neuron can change its state and output based on the states and outputs of its neighbors (adjacent knight's moves) according to the following transition rules:

$U_{t+1}(N_{i,j})=U_{t}(N_{i,j})+2-\sum _{N\in G(N_{i,j})}V_{t}(N)$

$V_{t+1}(N_{i,j})=\left\{{\begin{array}{ll}1&{\mbox{if}}\,\,U_{t+1}(N_{i,j})>3\\0&{\mbox{if}}\,\,U_{t+1}(N_{i,j})<0\\V_{t}(N_{i,j})&{\mbox{otherwise}},\end{array}}\right.$

where $t$ represents discrete intervals of time, $U(N_{i,j})$ is the state of the neuron connecting square $i$ to square $j$, $V(N_{i,j})$ is the output of the neuron from $i$ to $j$, and $G(N_{i,j})$ is the set of neighbors of the neuron.

Although divergent cases are possible, the network should eventually converge, which occurs when no neuron changes its state from time $t$ to $t+1$. When the network converges, a solution is found. The solution found by the network will be either a knight's tour, or a series of two or more independent knight's tours within the same board.

Warnsdorff's algorithm

A graphical representation of the Knight's Tour implemented using Warnsdorff's Algorithm. The numbers in red circles denote the number of next possible moves that the knight could make if it moves from the start position to the one with the circle on it.

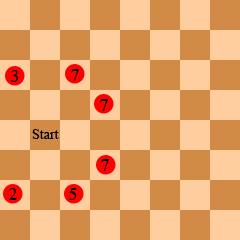
Warnsdorff's algorithm is a heuristic method for solving the knight's tour, based on the rule of choosing the square among those immediately accessible by the knight move that would give the fewest possible knight's moves following the move to that square. In graph-theoretic terms, each move is made to the adjacent vertex with the least degree. (Pohl has devised a rule for breaking ties.) This algorithm may also more generally be applied to any graph. Although the Hamiltonian path problem is NP-hard in general, on many graphs that occur in practice this heuristic is able to successfully locate a solution in linear time. The knight's tour is a special case.

The algorithm was first described in "Des Rösselsprungs einfachste und allgemeinste Lösung" by H. C. Warnsdorff in 1823.

Algorithm

Warnsdorff’s algorithm will do for any initial position of the knight on the board. All the possible squares which may be reached in one move from this position are located, and the number of moves that the knight would be able to make from each of these squares is found. Then, the algorithm dictates that the knight move to the square that has the least number of possible following moves. The process is then repeated until each square has been visited.

Some definitions:

• A position Q is accessible from a position P if P can move to Q by a single knight's move, and Q has not yet been visited.
• The accessibility of a position P is the number of positions accessible from P.

Algorithm:

1. set P to be a random initial position on the board
2. mark the board at P with the move number "1"
3. for each move number from 2 to the number of squares on the board:
   1. let S be the set of positions accessible from the input position
   2. set P to be the position in S with minimum accessibility
   3. mark the board at P with the current move number
4. return the marked board – each square will be marked with the move number on which it is visited.

See also

• Abu-Bakr Muhammad ben Yahya as-Suli
• George Koltanowski
• Longest uncrossed knight's path

External links

• Richard W. Henderson, Eugene Roger Apodaca A Knight of Egodeth: Zen Raptured Quietude, 240 Solutions to the Knights Tour in form of Game Book
• Warnsdorff's Rule and its efficiency from Warnsdorff's Rule Web Page
• Mario Velucchi The ultimate Knight's Tour page of Links
• The knight's tour
• Knight's tour notes
• Sloane's Integer Sequence OEIS: A001230
• Preprint of Pohl's paper (freely accessible)
• SilverKnight - online knight's tour game
• Knightfall - online version of the game as presented by the Riddler.

Implementations

• The Knight's Tour by Jay Warendorff, Wolfram Demonstrations Project
• A Simple backtracking implementation in C++
• A Simple implementation in standard Prolog
• An implementation in C#
• Knight's Tours Using a Neural Network Program that creates tours using a neural network, plus gallery of images.