5-orthoplex
| Regular pentacross (5-orthoplex) | |
|---|---|
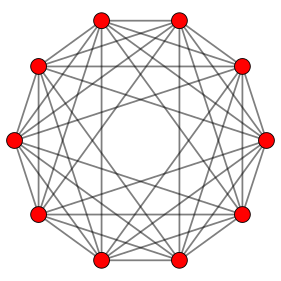 Orthogonal projection inside Petrie polygon | |
| Type | Regular 5-polytope |
| Family | orthoplex |
| Schläfli symbol | {3,3,3,4} {3,3,31,1} |
| Coxeter-Dynkin diagrams | |
| Hypercells | 32 {33} |
| Cells | 80 {3,3} |
| Faces | 80 {3} |
| Edges | 40 |
| Vertices | 10 |
| Vertex figure |  16-cell |
| Petrie polygon | decagon |
| Coxeter groups | C5, [3,3,3,4] D5, [32,1,1] |
| Dual | 5-cube |
| Properties | convex |
In five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell hypercells.
It has two constructed forms, the first being regular with Schläfli symbol {33,4}, and the second with alternately labeled (checkerboarded) facets, with Schläfli symbol {32,1,1} or Coxeter symbol 211.
Alternate names
- pentacross, derived from combining the family name cross polytope with pente for five (dimensions) in Greek.
- Triacontakaiditeron - as a 32-facetted 5-polytope (polyteron).
Related polytopes
It is a part of an infinite family of polytopes, called cross-polytopes or orthoplexes. The dual polytope is the 5-hypercube or penteract.
Construction
There are two Coxeter groups associated with the pentacross, one regular, dual of the penteract with the C5 or [4,3,3,3] Coxeter group, and a lower symmetry with two copies of 5-cell facets, alternating, with the D5 or [32,1,1] Coxeter group.
Cartesian coordinates
Cartesian coordinates for the vertices of a pentacross, centered at the origin are
- (±1,0,0,0,0), (0,±1,0,0,0), (0,0,±1,0,0), (0,0,0,±1,0), (0,0,0,0,±1)
Other images
| Coxeter plane | B5 | B4 / D5 | B3 / D4 / A2 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | [10] | [8] | [6] |
| Coxeter plane | B2 | A3 | |
| Graph | 
|

| |
| Dihedral symmetry | [4] | [4] |
 Precisely, the Perspective projection 3D to 2D of stereographic projection 4D to 3D of Schlegel diagram 5D to 4D of Pentacross. 10 sets of 4 edges forms 10 circles in the 4D Schlegel diagram: two of these circles are straight lines because contains the center of projection. |
Related polytopes
This polytope is one of 63 uniform polypeta generated from the B6 Coxeter plane, including the regular 6-cube or 6-orthoplex.
External links
- Olshevsky, George. "Cross polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Polytopes of Various Dimensions
- Multi-dimensional Glossary































