Resistor

A typical axial-lead resistor

Partially exposed Tesla TR-212 1 kΩ carbon film resistor

Axial-lead resistors on tape. The tape is removed during assembly before the leads are formed and the part is inserted into the board.

Three carbon composition resistors in a 1960s valve (vacuum tube) radio

A resistor is a two-terminal passive electronic component which implements electrical resistance as a circuit element. When a voltage V is applied across the terminals of a resistor, a current I will flow through the resistor in direct proportion to that voltage. This constant of proportionality is called conductance, G. The reciprocal of the conductance is known as the resistance R, since, with a given voltage V, a larger value of R further "resists" the flow of current I as given by Ohm's law:

$I={V \over R}$

Resistors are common elements of electrical networks and electronic circuits and are ubiquitous in most electronic equipment. Practical resistors can be made of various compounds and films, as well as resistance wire (wire made of a high-resistivity alloy, such as nickel-chrome). Resistors are also implemented within integrated circuits, particularly analog devices, and can also be integrated into hybrid and printed circuits.

The electrical functionality of a resistor is specified by its resistance: common commercial resistors are manufactured over a range of more than 9 orders of magnitude. When specifying that resistance in an electronic design, the required precision of the resistance may require attention to the manufacturing tolerance of the chosen resistor, according to its specific application. The temperature coefficient of the resistance may also be of concern in some precision applications. Practical resistors are also specified as having a maximum power rating which must exceed the anticipated power dissipation of that resistor in a particular circuit: this is mainly of concern in power electronics applications. Resistors with higher power ratings are physically larger and may require heat sinking. In a high voltage circuit, attention must sometimes be paid to the rated maximum working voltage of the resistor.

Practical resistors include a series inductance and a small parallel capacitance; these specifications can be important in high-frequency applications. In a low-noise amplifier or pre-amp the noise characteristics of a resistor may be an issue. The unwanted inductance, excess noise, and temperature coefficient are mainly dependent on the technology used in manufacturing the resistor. They are not normally specified individually for a particular family of resistors manufactured using a particular technology. A family of discrete resistors is also characterized according to its form factor, that is, the size of the device and position of its leads (or terminals) which is relevant in the practical manufacturing of circuits using them.

Units

The ohm (symbol: Ω) is the SI unit of electrical resistance, named after Georg Simon Ohm. An ohm is equivalent to a volt per ampere. Since resistors are specified and manufactured over a very large range of values, the derived units of milliohm (1 mΩ = 10⁻³ Ω), kilohm (1 kΩ = 10³ Ω), and megohm (1 MΩ = 10⁶ Ω) are also in common usage.

The reciprocal of resistance R is called conductance G = 1/R and is measured in Siemens (SI unit), sometimes referred to as a mho. Thus a Siemens is the reciprocal of an ohm: $S=\Omega ^{-1}$. Although the concept of conductance is often used in circuit analysis, practical resistors are always specified in terms of their resistance (ohms) rather than conductance.

Theory of operation

Ohm's law

The behavior of an ideal resistor is dictated by the relationship specified in Ohm's law:

$V=I\cdot R$

Ohm's law states that the voltage (V) across a resistor is proportional to the current (I) passing through it, where the constant of proportionality is the resistance (R).

Equivalently, Ohm's law can be stated:

$I={\frac {V}{R}}$

This formulation of Ohm's law states that, when a voltage (V) is present across a resistance (R), a current (I) will flow through the resistance. This is directly used in practical computations. For example, if a 300 ohm resistor is attached across the terminals of a 12 volt battery, then a current of 12 / 300 = 0.04 amperes (or 40 milliamperes) will flow through that resistor.

Series and parallel resistors

Main article: Series and parallel circuits

In a series configuration, the current through all of the resistors is the same, but the voltage across each resistor will be in proportion to its resistance. The potential difference (voltage) seen across the network is the sum of those voltages, thus the total resistance can be found as the sum of those resistances:

$R_{\mathrm {eq} }=R_{1}+R_{2}+\cdots +R_{n}$

As a special case, the resistance of N resistors connected in series, each of the same resistance R, is given by NR.

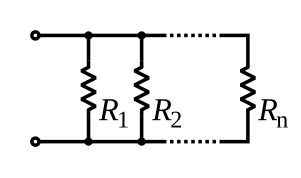
Resistors in a parallel configuration are each subject to the same potential difference (voltage), however the currents through them add. The conductances of the resistors then add to determine the conductance of the network. Thus the equivalent resistance (R_eq) of the network can be computed:

${\frac {1}{R_{\mathrm {eq} }}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\cdots +{\frac {1}{R_{n}}}$

The parallel equivalent resistance can be represented in equations by two vertical lines "||" (as in geometry) as a simplified notation. For the case of two resistors in parallel, this can be calculated using:

$R_{\mathrm {eq} }=R_{1}\|R_{2}={R_{1}R_{2} \over R_{1}+R_{2}}$

As a special case, the resistance of N resistors connected in parallel, each of the same resistance R, is given by R/N.

A resistor network that is a combination of parallel and series connections can be broken up into smaller parts that are either one or the other. For instance,

$R_{\mathrm {eq} }=\left(R_{1}\|R_{2}\right)+R_{3}={R_{1}R_{2} \over R_{1}+R_{2}}+R_{3}$

However, some complex networks of resistors cannot be resolved in this manner, requiring more sophisticated circuit analysis. For instance, consider a cube, each edge of which has been replaced by a resistor. What then is the resistance that would be measured between two opposite vertices? In the case of 12 equivalent resistors, it can be shown that the corner-to-corner resistance is ⁵⁄₆ of the individual resistance. More generally, the Y-Δ transform, or matrix methods can be used to solve such a problem.

One practical application of these relationships is that a non-standard value of resistance can generally be synthesized by connecting a number of standard values in series and/or parallel. This can also be used to obtain a resistance with a higher power rating than that of the individual resistors used. In the special case of N identical resistors all connected in series or all connected in parallel, the power rating of the individual resistors is thereby multiplied by N.

Power dissipation

The power P dissipated by a resistor (or the equivalent resistance of a resistor network) is calculated as: $P=I^{2}R=IV={\frac {V^{2}}{R}}$

The first form is a restatement of Joule's first law. Using Ohm's law, the two other forms can be derived.

The total amount of heat energy released over a period of time can be determined from the integral of the power over that period of time:

$W=\int _{t_{1}}^{t_{2}}v(t)i(t)\,dt.$

Practical resistors are rated according to their maximum power dissipation. The vast majority of resistors used in electronic circuits absorb much less than a watt of electrical power and require no attention to their power rating. Such resistors in their discrete form, including most of the packages detailed below, are typically rated as 1/10, 1/8, or 1/4 watt.

Resistors required to dissipate substantial amounts of power, particularly used in power supplies, power conversion circuits, and power amplifiers, are generally referred to as power resistors; this designation is loosely applied to resistors with power ratings of 1 watt or greater. Power resistors are physically larger and tend not to use the preferred values, color codes, and external packages described below.

If the average power dissipated by a resistor is more than its power rating, damage to the resistor may occur, permanently altering its resistance; this is distinct from the reversible change in resistance due to its temperature coefficient when it warms. Excessive power dissipation may raise the temperature of the resistor to a point where it can burn the circuit board or adjacent components, or even cause a fire. There are flameproof resistors that fail (open circuit) before they overheat dangerously.

Note that the nominal power rating of a resistor is not the same as the power that it can safely dissipate in practical use. Air circulation and proximity to a circuit board, ambient temperature, and other factors can reduce acceptable dissipation significantly. Rated power dissipation may be given for an ambient temperature of 25 °C in free air. Inside an equipment case at 60 °C, rated dissipation will be significantly less; a resistor dissipating a bit less than the maximum figure given by the manufacturer may still be outside the safe operating area and may prematurely fail.(kavimani )

Construction

A single in line (SIL) resistor package with 8 individual, 47 ohm resistors. One end of each resistor is connected to a separate pin and the other ends are all connected together to the remaining (common) pin - pin 1, at the end identified by the white dot.

Lead arrangements

Resistors with wire leads for through-hole mounting

Through-hole components typically have leads leaving the body axially. Others have leads coming off their body radially instead of parallel to the resistor axis. Other components may be SMT (surface mount technology) while high power resistors may have one of their leads designed into the heat sink.

Carbon composition

Carbon composition resistors consist of a solid cylindrical resistive element with embedded wire leads or metal end caps to which the lead wires are attached. The body of the resistor is protected with paint or plastic. Early 20th-century carbon composition resistors had uninsulated bodies; the lead wires were wrapped around the ends of the resistance element rod and soldered. The completed resistor was painted for color coding of its value.

The resistive element is made from a mixture of finely ground (powdered) carbon and an insulating material (usually ceramic). A resin holds the mixture together. The resistance is determined by the ratio of the fill material (the powdered ceramic) to the carbon. Higher concentrations of carbon, a weak conductor, result in lower resistance. Carbon composition resistors were commonly used in the 1960s and earlier, but are not so popular for general use now as other types have better specifications, such as tolerance, voltage dependence, and stress (carbon composition resistors will change value when stressed with over-voltages). Moreover, if internal moisture content (from exposure for some length of time to a humid environment) is significant, soldering heat will create a non-reversible change in resistance value. Carbon composition resistors have poor stability with time and were consequently factory sorted to, at best, only 5% tolerance. These resistors, however, if never subjected to overvoltage nor overheating were remarkably reliable considering the component's size

They are still available, but comparatively quite costly. Values ranged from fractions of an ohm to 22 megohms. Because of the high price, these resistors are no longer used in most applications. However, carbon resistors are used in power supplies and welding controls.

Carbon film

A carbon film is deposited on an insulating substrate, and a helix cut in it to create a long, narrow resistive path. Varying shapes, coupled with the resistivity of carbon, (ranging from 90 to 400 nΩ m) can provide a variety of resistances. Carbon film resistors feature a power rating range of 0.125 W to 5 W at 70 °C. Resistances available range from 1 ohm to 10 megohm. The carbon film resistor has an operating temperature range of -55 °C to 155 °C. It has 200 to 600 volts maximum working voltage range. Special carbon film resistors are used in applications requiring high pulse stability.

Thick and thin film

Thick film resistors became popular during the 1970s, and most SMD (surface mount device) resistors today are of this type. The principal difference between thin film and thick film resistors is not the actual thickness of the film, but rather how the film is applied to the cylinder (axial resistors) or the surface (SMD resistors).

Thin film resistors are made by sputtering (a method of vacuum deposition) the resistive material onto an insulating substrate. The film is then etched in a similar manner to the old (subtractive) process for making printed circuit boards; that is, the surface is coated with a photo-sensitive material, then covered by a pattern film, irradiated with ultraviolet light, and then the exposed photo-sensitive coating is developed, and underlying thin film is etched away.

Thick film resistors are manufactured using screen and stencil printing processes.

Because the time during which the sputtering is performed can be controlled, the thickness of the thin film can be accurately controlled. The type of material is also usually different consisting of one or more ceramic (cermet) conductors such as tantalum nitride (TaN), ruthenium oxide (RuO₂), lead oxide (PbO), bismuth ruthenate (Bi₂Ru₂O₇), nickel chromium (NiCr), and/or bismuth iridate (Bi₂Ir₂O₇).

The resistance of both thin and thick film resistors after manufacture is not highly accurate; they are usually trimmed to an accurate value by abrasive or laser trimming. Thin film resistors are usually specified with tolerances of 0.1, 0.2, 0.5, or 1%, and with temperature coefficients of 5 to 25 ppm/K.

Thick film resistors may use the same conductive ceramics, but they are mixed with sintered (powdered) glass and some kind of liquid so that the composite can be screen-printed. This composite of glass and conductive ceramic (cermet) material is then fused (baked) in an oven at about 850 °C.

Thick film resistors, when first manufactured, had tolerances of 5%, but standard tolerances have improved to 2% or 1% in the last few decades. Temperature coefficients of thick film resistors are high, typically ±200 or ±250 ppm/K; a 40 kelvin (70 °F) temperature change can change the resistance by 1%.

Thin film resistors are usually far more expensive than thick film resistors. For example, SMD thin film resistors, with 0.5% tolerances, and with 25 ppm/K temperature coefficients, when bought in full size reel quantities, are about twice the cost of 1%, 250 ppm/K thick film resistors.

Metal film

A common type of axial resistor today is referred to as a metal-film resistor. Metal electrode leadless face (MELF) resistors often use the same technology, but are a cylindrically shaped resistor designed for surface mounting. Note that other types of resistors (e.g., carbon composition) are also available in MELF packages.

Metal film resistors are usually coated with nickel chromium (NiCr), but might be coated with any of the cermet materials listed above for thin film resistors. Unlike thin film resistors, the material may be applied using different techniques than sputtering (though that is one such technique). Also, unlike thin-film resistors, the resistance value is determined by cutting a helix through the coating rather than by etching. (This is similar to the way carbon resistors are made.) The result is a reasonable tolerance (0.5, 1, or 2%) and a temperature coefficient that is generally between 50 and 100 ppm/K. Metal film resistors possess good noise characteristics and low non-linearity due to a low voltage coefficient. Also beneficial are the components efficient tolerance, temperature coefficient and stability.

Metal Oxide film

Metal-Oxide film resistors resemble Metal film types, but are made of metal oxides such as tin oxide. This results in a higher operating temperature and greater stability/reliability than Metal film. They are used in applications with high endurance demands.

Wirewound

Types of windings in wire resistors:
1 - common
2 - bifilar
3 - common on a thin former
4 - Ayrton-Perry

Wirewound resistors are commonly made by winding a metal wire, usually nichrome, around a ceramic, plastic, or fiberglass core. The ends of the wire are soldered or welded to two caps or rings, attached to the ends of the core. The assembly is protected with a layer of paint, molded plastic, or an enamel coating baked at high temperature. Because of the very high surface temperature these resistors can withstand temperatures of up to +450 °C. Wire leads in low power wirewound resistors are usually between 0.6 and 0.8 mm in diameter and tinned for ease of soldering. For higher power wirewound resistors, either a ceramic outer case or an aluminum outer case on top of an insulating layer is used. The aluminum-cased types are designed to be attached to a heat sink to dissipate the heat; the rated power is dependent on being used with a suitable heat sink, e.g., a 50 W power rated resistor will overheat at a fraction of the power dissipation if not used with a heat sink. Large wirewound resistors may be rated for 1,000 watts or more.

Because wirewound resistors are coils they have more undesirable inductance than other types of resistor, although winding the wire in sections with alternately reversed direction can minimize inductance. Other techniques employ bifilar winding, or a flat thin former (to reduce cross-section area of the coil). For most demanding circuits resistors with Ayrton-Perry winding are used.

Applications of wirewound resistors are similar to those of composition resistors with the exception of the high frequency. The high frequency of wirewound resistors is substantially worse than that of a composition resistor.

Foil resistor

The primary resistance element of a foil resistor is a special alloy foil several micrometres thick. Since their introduction in the 1960s, foil resistors have had the best precision and stability of any resistor available. One of the important parameters influencing stability is the temperature coefficient of resistance (TCR). The TCR of foil resistors is extremely low, and has been further improved over the years. One range of ultra-precision foil resistors offers a TCR of 0.14 ppm/°C, tolerance ±0.005%, long-term stability (1 year) 25 ppm, (3 year) 50 ppm (further improved 5-fold by hermetic sealing), stability under load (2000 hours) 0.03%, thermal EMF 0.1 μV/°C, noise -42 dB, voltage coefficient 0.1 ppm/V, inductance 0.08 μH, capacitance 0.5 pF.

Ammeter shunts

An ammeter shunt is a special type of current-sensing resistor, having four terminals and a value in milliohms or even micro-ohms. Current-measuring instruments, by themselves, can usually accept only limited currents. To measure high currents, the current passes through the shunt, where the voltage drop is measured and interpreted as current. A typical shunt consists of two solid metal blocks, sometimes brass, mounted on to an insulating base. Between the blocks, and soldered or brazed to them, are one or more strips of low temperature coefficient of resistance (TCR) manganin alloy. Large bolts threaded into the blocks make the current connections, while much-smaller screws provide voltage connections. Shunts are rated by full-scale current, and often have a voltage drop of 50 mV at rated current. Such meters are adapted to the shunt full current rating by using an appropriately marked dial face; no change need be made to the other parts of the meter.

Grid resistor

In heavy-duty industrial high-current applications, a grid resistor is a large convection-cooled lattice of stamped metal alloy strips connected in rows between two electrodes. Such industrial grade resistors can be as large as a refrigerator; some designs can handle over 500 amperes of current, with a range of resistances extending lower than 0.04 ohms. They are used in applications such as dynamic braking and load banking for locomotives and trams, neutral grounding for industrial AC distribution, control loads for cranes and heavy equipment, load testing of generators and harmonic filtering for electric substations.

The term grid resistor is sometimes used to describe a resistor of any type connected to the control grid of a vacuum tube. This is not a resistor technology; it is an electronic circuit topology.

Special varieties

• Metal oxide varistor
• Cermet
• Phenolic
• Tantalum
• Water resistor

Variable resistors

Adjustable resistors

A resistor may have one or more fixed tapping points so that the resistance can be changed by moving the connecting wires to different terminals. Some wirewound power resistors have a tapping point that can slide along the resistance element, allowing a larger or smaller part of the resistance to be used.

Where continuous adjustment of the resistance value during operation of equipment is required, the sliding resistance tap can be connected to a knob accessible to an operator. Such a device is called a rheostat and has two terminals.

Potentiometers

Main article: Potentiometer

A common element in electronic devices is a three-terminal resistor with a continuously adjustable tapping point controlled by rotation of a shaft or knob. These variable resistors are known as potentiometers when all three terminals are present, since they act as a continuously adjustable voltage divider. A common example is a volume control for a radio receiver.

Accurate, high-resolution panel-mounted potentiometers (or "pots") have resistance elements typically wirewound on a helical mandrel, although some include a conductive-plastic resistance coating over the wire to improve resolution. These typically offer ten turns of their shafts to cover their full range. They are usually set with dials that include a simple turns counter and a graduated dial. Electronic analog computers used them in quantity for setting coefficients, and delayed-sweep oscilloscopes of recent decades included one on their panels.

Resistance decade boxes

A resistance decade box or resistor substitution box is a unit containing resistors of many values, with one or more mechanical switches which allow any one of various discrete resistances offered by the box to be dialed in. Usually the resistance is accurate to high precision, ranging from laboratory/calibration grade accuracy of 20 parts per million, to field grade at 1%. Inexpensive boxes with lesser accuracy are also available. All types offer a convenient way of selecting and quickly changing a resistance in laboratory, experimental and development work without needing to attach resistors one by one, or even stock each value. The range of resistance provided, the maximum resolution, and the accuracy characterize the box. For example, one box offers resistances from 0 to 24 megohms, maximum resolution 0.1 ohm, accuracy 0.1%.

Special devices

There are various devices whose resistance changes with various quantities. The resistance of thermistors exhibit a strong negative temperature coefficient, making them useful for measuring temperatures. Since their resistance can be large until they are allowed to heat up due to the passage of current, they are also commonly used to prevent excessive current surges when equipment is powered on. Similarly, the resistance of a humistor varies with humidity. Metal oxide varistors drop to a very low resistance when a high voltage is applied, making them useful for protecting electronic equipment by absorbing dangerous voltage surges. One sort of photodetector, the photoresistor, has a resistance which varies with illumination.

The strain gauge, invented by Edward E. Simmons and Arthur C. Ruge in 1938, is a type of resistor that changes value with applied strain. A single resistor may be used, or a pair (half bridge), or four resistors connected in a Wheatstone bridge configuration. The strain resistor is bonded with adhesive to an object that will be subjected to mechanical strain. With the strain gauge and a filter, amplifier, and analog/digital converter, the strain on an object can be measured.

A related but more recent invention uses a Quantum Tunnelling Composite to sense mechanical stress. It passes a current whose magnitude can vary by a factor of 10¹² in response to changes in applied pressure.

Measurement

The value of a resistor can be measured with an ohmmeter, which may be one function of a multimeter. Usually, probes on the ends of test leads connect to the resistor. A simple ohmmeter may apply a voltage from a battery across the unknown resistor (with an internal resistor of a known value in series) producing a current which drives a meter movement. The current flow, in accordance with Ohm's Law, is inversely proportional to the sum of the internal resistance and the resistor being tested, resulting in an analog meter scale which is very non-linear, calibrated from infinity to 0 ohms. A digital multimeter, using active electronics, may instead pass a specified current through the test resistance. The voltage generated across the test resistance in that case is linearly proportional to its resistance, which is measured and displayed. In either case the low-resistance ranges of the meter pass much more current through the test leads than do high-resistance ranges, in order for the voltages present to be at reasonable levels (generally below 10 volts) but still measurable.

Measuring low-value resistors, such as fractional-ohm resistors, with acceptable accuracy requires four-terminal connections. One pair of terminals applies a known, calibrated current to the resistor, while the other pair senses the voltage drop across the resistor. Some laboratory quality ohmmeters, especially milliohmmeters, and even some of the better digital multimeters sense using four input terminals for this purpose, which may be used with special test leads. Each of the two so-called Kelvin clips has a pair of jaws insulated from each other. One side of each clip applies the measuring current, while the other connections are only to sense the voltage drop. The resistance is again calculated using Ohm's Law as the measured voltage divided by the applied current.

Standards

Production resistors

Resistor characteristics are quantified and reported using various national standards. In the US, MIL-STD-202 contains the relevant test methods to which other standards refer.

There are various standards specifying properties of resistors for use in equipment:

• BS 1852
• EIA-RS-279
• MIL-PRF-26
• MIL-PRF-39007 (Fixed Power, established reliability)
• MIL-PRF-55342 (Surface-mount thick and thin film)
• MIL-PRF-914
• MIL-R-11
• MIL-R-39017 (Fixed, General Purpose, Established Reliability)
• MIL-PRF-32159 (zero ohm jumpers)

There are other United States military procurement MIL-R- standards.

Resistance standards

The primary standard for resistance, the "mercury ohm" was initially defined in 1884 in as a column of mercury 106 mm long and 1 square millimeter in cross-section, at 0 degrees Celsius. Difficulties in precisely measuring the physical constants to replicate this standard result in variations of as much as 30 ppm. From 1900 the mercury ohm was replaced with a precision machined plate of manganin. Since 1990 the international resistance standard has been based on the quantized Hall effect discovered by Klaus von Klitzing, for which he won the Nobel Prize in Physics in 1985.

Resistors of extremely high precision are manufactured for calibration and laboratory use. They may have four terminals, using one pair to carry an operating current and the other pair to measure the voltage drop; this eliminates errors caused by voltage drops across the lead resistances, because no current flows through voltage sensing leads. It is important in small value resistors (100–0.0001 ohm) where lead resistance is significant or even comparable with respect to resistance standard value.

Resistor marking

Main article: Electronic color code

Most axial resistors use a pattern of colored stripes to indicate resistance. Surface-mount resistors are marked numerically, if they are big enough to permit marking; more-recent small sizes are impractical to mark. Cases are usually tan, brown, blue, or green, though other colors are occasionally found such as dark red or dark gray.

Early 20th century resistors, essentially uninsulated, were dipped in paint to cover their entire body for color coding. A second color of paint was applied to one end of the element, and a color dot (or band) in the middle provided the third digit. The rule was "body, tip, dot", providing two significant digits for value and the decimal multiplier, in that sequence. Default tolerance was ±20%. Closer-tolerance resistors had silver (±10%) or gold-colored (±5%) paint on the other end.

Four-band resistors

Four-band identification is the most commonly used color-coding scheme on resistors. It consists of four colored bands that are painted around the body of the resistor. The first two bands encode the first two significant digits of the resistance value, the third is a power-of-ten multiplier or number-of-zeroes, and the fourth is the tolerance accuracy, or acceptable error, of the value. The first three bands are equally spaced along the resistor; the spacing to the fourth band is wider. Sometimes a fifth band identifies the thermal coefficient, but this must be distinguished from the true 5-color system, with 3 significant digits.

For example, green-blue-yellow-red is 56×10⁴ Ω = 560 kΩ ± 2%. An easier description can be as followed: the first band, green, has a value of 5 and the second band, blue, has a value of 6, and is counted as 56. The third band, yellow, has a value of 10⁴, which adds four 0's to the end, creating 560,000 Ω at ±2% tolerance accuracy. 560,000 Ω changes to 560 kΩ ±2% (as a kilo- is 10³).

Each color corresponds to a certain digit, progressing from darker to lighter colors, as shown in the chart below.

Color	1st band	2nd band	3rd band (multiplier)	4th band (tolerance)	Temp. Coefficient
Black	0	0	×100
Brown	1	1	×101	±1% (F)	100 ppm
Red	2	2	×102	±2% (G)	50 ppm
Orange	3	3	×103		15 ppm
Yellow	4	4	×104		25 ppm
Green	5	5	×105	±0.5% (D)
Blue	6	6	×106	±0.25% (C)
Violet	7	7	×107	±0.1% (B)
Gray	8	8	×108	±0.05% (A)
White	9	9	×109
Gold			×10−1	±5% (J)
Silver			×10−2	±10% (K)
None				±20% (M)

There are many mnemonics for remembering these colors.

Preferred values

Main article: Preferred number

Early resistors were made in more or less arbitrary round numbers; a series might have 100, 125, 150, 200, 300, etc. Resistors as manufactured are subject to a certain percentage tolerance, and it makes sense to manufacture values that correlate with the tolerance, so that the actual value of a resistor overlaps slightly with its neighbors. Wider spacing leaves gaps; narrower spacing increases manufacturing and inventory costs to provide resistors that are more or less interchangeable.

A logical scheme is to produce resistors in a range of values which increase in a geometrical progression, so that each value is greater than its predecessor by a fixed multiplier or percentage, chosen to match the tolerance of the range. For example, for a tolerance of ±20% it makes sense to have each resistor about 1.5 times its predecessor, covering a decade in 6 values. In practice the factor used is 1.4678, giving values of 1.47, 2.15, 3.16, 4.64, 6.81, 10 for the 1–10 decade (a decade is a range increasing by a factor of 10; 0.1–1 and 10–100 are other examples); these are rounded in practice to 1.5, 2.2, 3.3, 4.7, 6.8, 10; followed, of course by 15, 22, 33, … and preceded by … 0.47, 0.68, 1. This scheme has been adopted as the E6 series of the IEC 60063 preferred number values. There are also E12, E24, E48, E96 and E192 series for components of ever tighter tolerance, with 12, 24, 96, and 192 different values within each decade. The actual values used are in the IEC 60063 lists of preferred numbers.

A resistor of 100 ohms ±20% would be expected to have a value between 80 and 120 ohms; its E6 neighbors are 68 (54-82) and 150 (120-180) ohms. A sensible spacing, E6 is used for ±20% components; E12 for ±10%; E24 for ±5%; E48 for ±2%, E96 for ±1%; E192 for ±0.5% or better. Resistors are manufactured in values from a few milliohms to about a gigaohm in IEC60063 ranges appropriate for their tolerance.

Earlier power wirewound resistors, such as brown vitreous-enameled types, however, were made with a different system of preferred values, such as some of those mentioned in the first sentence of this section.

5-band axial resistors

5-band identification is used for higher precision (lower tolerance) resistors (1%, 0.5%, 0.25%, 0.1%), to specify a third significant digit. The first three bands represent the significant digits, the fourth is the multiplier, and the fifth is the tolerance. Five-band resistors with a gold or silver 4th band are sometimes encountered, generally on older or specialized resistors. The 4th band is the tolerance and the 5th the temperature coefficient.

SMD resistors

This image shows four surface-mount resistors (the component at the upper left is a capacitor) including two zero-ohm resistors. Zero-ohm links are often used instead of wire links, so that they can be inserted by a resistor-inserting machine. Of course, their resistance is non-zero, although quite low. Zero is simply a brief description of their function.

Surface mounted resistors are printed with numerical values in a code related to that used on axial resistors. Standard-tolerance surface-mount technology (SMT) resistors are marked with a three-digit code, in which the first two digits are the first two significant digits of the value and the third digit is the power of ten (the number of zeroes). For example:

334	= 33 × 104 ohms = 330 kilohms
222	= 22 × 102 ohms = 2.2 kilohms
473	= 47 × 103 ohms = 47 kilohms
105	= 10 × 105 ohms = 1.0 megohm

Resistances less than 100 ohms are written: 100, 220, 470. The final zero represents ten to the power zero, which is 1. For example:

100	= 10 × 100 ohm = 10 ohms
220	= 22 × 100 ohm = 22 ohms

Sometimes these values are marked as 10 or 22 to prevent a mistake.

Resistances less than 10 ohms have 'R' to indicate the position of the decimal point (radix point). For example:

4R7	= 4.7 ohms
R300	= 0.30 ohms
0R22	= 0.22 ohms
0R01	= 0.01 ohms

Precision resistors are marked with a four-digit code, in which the first three digits are the significant figures and the fourth is the power of ten. For example:

1001	= 100 × 101 ohms = 1.00 kilohm
4992	= 499 × 102 ohms = 49.9 kilohm
1000	= 100 × 100 ohm = 100 ohms

000 and 0000 sometimes appear as values on surface-mount zero-ohm links, since these have (approximately) zero resistance.

More recent surface-mount resistors are too small, physically, to permit practical markings to be applied.

Industrial type designation

Format: [two letters]<space>[resistance value (three digit)]<nospace>[tolerance code(numerical - one digit)]

Power Rating at 70 °C

Type No.	Power rating (watts)	MIL-R-11 Style	MIL-R-39008 Style
BB	⅛	RC05	RCR05
CB	¼	RC07	RCR07
EB	½	RC20	RCR20
GB	1	RC32	RCR32
HB	2	RC42	RCR42
GM	3	-	-
HM	4	-	-

Tolerance Code

Industrial type designation	Tolerance	MIL Designation
5	±5%	J
2	±20%	M
1	±10%	K
-	±2%	G
-	±1%	F
-	±0.5%	D
-	±0.25%	C
-	±0.1%	B

The operational temperature range distinguishes commercial grade, industrial grade and military grade components.

• Commercial grade: 0 °C to 70 °C
• Industrial grade: −40 °C to 85 °C (sometimes −25 °C to 85 °C)
• Military grade: −55 °C to 125 °C (sometimes -65 °C to 275 °C)
• Standard Grade -5 °C to 60 °C

Electrical and thermal noise

In amplifying faint signals, it is often necessary to minimize electronic noise, particularly in the first stage of amplification. As dissipative elements, even an ideal resistor will naturally produce a randomly fluctuating voltage or "noise" across its terminals. This Johnson–Nyquist noise is a fundamental noise source which depends only upon the temperature and resistance of the resistor, and is predicted by the fluctuation–dissipation theorem. Using a larger resistor produces a larger voltage noise, whereas with a smaller value of resistance there will be more current noise, assuming a given temperature. The thermal noise of a practical resistor may also be somewhat larger than the theoretical prediction and that increase is typically frequency-dependent.

However the "excess noise" of a practical resistor is an additional source of noise observed only when a current flows through it. This is specified in unit of μV/V/decade - μV of noise per volt applied across the resistor per decade of frequency. The μV/V/decade value is frequently given in dB so that a resistor with a noise index of 0 dB will exhibit 1 μV (rms) of excess noise for each volt across the resistor in each frequency decade. Excess noise is thus an example of 1/f noise. Thick-film and carbon composition resistors generate more excess noise than other types at low frequencies; wire-wound and thin-film resistors, though much more expensive, are often utilized for their better noise characteristics. Carbon composition resistors can exhibit a noise index of 0 dB while bulk metal foil resistors may have a noise index of -40 dB, usually making the excess noise of metal foil resistors insignificant. Thin film surface mount resistors typically have lower noise and better thermal stability than thick film surface mount resistors. However, the design engineer must read the data sheets for the family of devices to weigh the various device tradeoffs.

While not an example of "noise" per se, a resistor may act as a thermocouple, producing a small DC voltage differential across it due to the thermoelectric effect if its ends are at somewhat different temperatures. This induced DC voltage can degrade the precision of instrumentation amplifiers in particular. Such voltages appear in the junctions of the resistor leads with the circuit board and with the resistor body. Common metal film resistors show such an effect at a magnitude of about 20 µV/°C. Some carbon composition resistors can exhibit thermoelectric offsets as high as 400 µV/°C, whereas specially constructed resistors can reduce this number to 0.05 µV/°C. In applications where the thermoelectric effect may become important, care has to be taken (for example) to mount the resistors horizontally to avoid temperature gradients and to mind the air flow over the board.

Failure modes

The failure rate of resistors in a properly designed circuit is low compared to other electronic components such as semiconductors and electrolytic capacitors. Damage to resistors most often occurs due to overheating when the average power delivered to it (as computed above) greatly exceeds its ability to dissipate heat (specified by the resistor's power rating). This may be due to a fault external to the circuit, but is frequently caused by the failure of another component (such as a transistor that shorts out) in the circuit connected to the resistor. Operating a resistor too close to its power rating can limit the resistor's lifespan or cause a change in its resistance over time which may or may not be noticeable. A safe design generally uses overrated resistors in power applications to avoid this danger.

When overheated, carbon-film resistors may decrease or increase in resistance. Carbon film and composition resistors can fail (open circuit) if running close to their maximum dissipation. This is also possible but less likely with metal film and wirewound resistors.

There can also be failure of resistors due to mechanical stress and adverse environmental factors including humidity. If not enclosed, wirewound resistors can corrode.

Variable resistors degrade in a different manner, typically involving poor contact between the wiper and the body of the resistance. This may be due to dirt or corrosion and is typically perceived as "crackling" as the contact resistance fluctuates; this is especially noticed as the device is adjusted. This is similar to crackling caused by poor contact in switches, and like switches, potentiometers are to some extent self-cleaning: running the wiper across the resistance may improve the contact. Potentiometers which are seldom adjusted, especially in dirty or harsh environments, are most likely to develop this problem. When self-cleaning of the contact is insufficient, improvement can usually be obtained through the use of contact cleaner (also known as "tuner cleaner") spray. The crackling noise associated with turning the shaft of a dirty potentiometer in an audio circuit (such as the volume control) is greatly accentuated when an undesired DC voltage is present, often implicating the failure of a DC blocking capacitor in the circuit.

See also

• Circuit design
• Electrical resistance
• Electrical impedance
• Iron-hydrogen resistor
• Memristor
• Photoresistor
• Resistivity
• Shot noise
• Thermistor
• Trimmer
• Varistor
• Dummy load

External links

• 4-terminal resistors - How ultra-precise resistors work
• Beginner's guide to potentiometers, including description of different tapers
• Color Coded Resistance Calculator
• Resistor Types - Does It Matter?
• Ask The Applications Engineer - Difference between types of resistors
• Resistors and their uses
• A very well illustrated tutorial about Resistors, Volt and Current