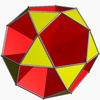
Icosidodecahedron

Icosidodecahedron
(Click here for rotating model)
Type	Archimedean solid Uniform polyhedron
Elements	F = 32, E = 60, V = 30 (χ = 2)
Faces by sides	20{3}+12{5}
Conway notation	aD
Schläfli symbols	r{5,3}
Schläfli symbols	t₁{5,3}
Wythoff symbol	2 \| 3 5
Coxeter diagram
Symmetry group	I_h, H₃, [5,3], (*532), order 120
Rotation group	I, [5,3]⁺, (532), order 60
Dihedral angle	${\begin{aligned}&\cos ^{-1}\left(-{\sqrt {\frac {5+2{\sqrt {5}}}{15}}}\right)\\[2pt]&\approx 142.62^{\circ }\end{aligned}}$
References	U₂₄, C₂₈, W₁₂
Properties	Semiregular convex quasiregular
Colored faces	3.5.3.5 (Vertex figure)
Rhombic triacontahedron (dual polyhedron)	Net

In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such it is one of the Archimedean solids and more particularly, a quasiregular polyhedron.

An icosidodecahedron has icosahedral symmetry, and its first stellation is the compound of a dodecahedron and its dual icosahedron, with the vertices of the icosahedron located at the midpoints of the edges of either.

Its dual polyhedron is the rhombic triacontahedron. An icosidodecahedron can be split along any of six planes to form a pair of pentagonal rotundae, which belong among the Johnson solids.

The icosidodecahedron can be considered a pentagonal gyrobirotunda, as a combination of two rotundae (compare pentagonal orthobirotunda, one of the Johnson solids).

The wire frame figure of the icosidodecahedron consists of six flat regular decagons, meeting in pairs at each of the 30 vertices.

In four-dimensional geometry the icosidodecahedron appears in the regular 600-cell as the equatorial slice that belongs to the vertex-first passage of the 600-cell through 3D space. In other words: the 30 vertices of the 600-cell which lie at arc distances of 90 degrees on its circumscribed hypersphere from a pair of opposite vertices, are the vertices of an icosidodecahedron. The wire frame figure of the 600-cell consists of 72 flat regular decagons. Six of these are the equatorial decagons to a pair of opposite vertices. They are precisely the six decagons which form the wire frame figure of the icosidodecahedron.

Cartesian coordinates

Convenient Cartesian coordinates for the vertices of an icosidodecahedron with unit edges are given by

(0,0,±τ)
(0,±τ,0)
(±τ,0,0)
(±1/2, ±τ/2, ±(1+τ)/2)
(±τ/2, ±(1+τ)/2, ±1/2)
(±(1+τ)/2, ±1/2, ±τ/2)

where τ is the golden ratio, (1+√5)/2.

Surface area and volume

The surface area A and the volume V of the icosidodecahedron of edge length a are:

A=(5{\sqrt {3}}+3{\sqrt {25+10{\sqrt {5}}}})a^{2}\approx 29.3059828a^{2}

V={\frac {1}{6}}(45+17{\sqrt {5}})a^{3}\approx 13.8355259a^{3}.

Related polyhedra

The icosidodecahedron is a rectified dodecahedron and also a rectified icosahedron, existing as the full-edge truncation between these regular solids.

The Icosidodecahedron contains 12 pentagons of the dodecahedron and 20 triangles of the icosahedron:

Picture	Dodecahedron	Truncated dodecahedron	Icosidodecahedron	Truncated icosahedron	Icosahedron
Coxeter-Dynkin

Pentagonal gyrobirotunda

It is also related to the Johnson solid called a pentagonal orthobirotunda created by two pentagonal rotunda connected as mirror images.

(Dissection)

Icosidodecahedron
(pentagonal gyrobirotunda)

Pentagonal orthobirotunda

Pentagonal rotunda

Eight uniform star polyhedra share the same vertex arrangement. Of these, two also share the same edge arrangement: the small icosihemidodecahedron (having the triangular faces in common), and the small dodecahemidodecahedron (having the pentagonal faces in common). The vertex arrangement is also shared with the compounds of five octahedra and of five tetrahemihexahedra.

Icosidodecahedra in reality and games

In Sonic Colors, a type of obstacle that only appears in Starlight Carnival Act 4 is an icosidodecahedron that has Frusta caved in its pentagonal faces. The obstacle shoots energy balls in a spiral.

References

Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)

External links

Weisstein, Eric W., "Icosidodecahedron" ("Archimedean solid") at MathWorld.
Klitzing, Richard. "3D convex uniform polyhedra o3x5o - id".
The Uniform Polyhedra
Virtual Reality Polyhedra The Encyclopedia of Polyhedra

Icosidodecahedron	Small icosihemidodecahedron	Small dodecahemidodecahedron
Great icosidodecahedron	Great dodecahemidodecahedron	Great icosihemidodecahedron
Dodecadodecahedron	Small dodecahemicosahedron	Great dodecahemicosahedron
Compound of five octahedra	Compound of five tetrahemihexahedra