Waterman butterfly projection
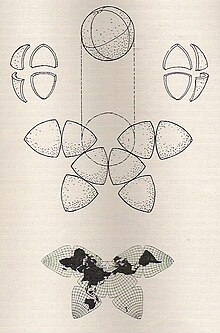
The Waterman "Butterfly" World Map Projection was created by Steve Waterman and published in 1996. It is an octahedral transformation of a globe, reviving the Butterfly Map principle first developed by Bernard J.S. Cahill (1866–1944) in 1909. Cahill and Waterman maps can each be shown in various profiles, typically linked at the north Pacific or north Atlantic oceans.
Whereas Cahill's approach was that of an architect, Waterman derived his design from his work on close-packing of spheres. This involved the interpretation of a spherical extraction from cubic closest packed spheres, into a corresponding convex hull. Then for its projection; straight lines were used to define each 5 x 5 section onto this convex hull.
Projection employed an equal length delineation approach for the equator. Latitudes were drawn in three straight line sections (in each octant) - from pole to fold-line, fold-line to largest line parallel to equator, and then from there to the equator. The largest line parallel to the equator also has equal length delinations. One particular Waterman polyhedron best served to minimize land sinuses (breaking up of land masses) and was therefore chosen.
Like Buckminster Fuller's 1943 Dymaxion Projection, an octahedral Butterfly Map can show all the continents uninterrupted if its octants are divided at the proper meridian, that is, 20° W, and joined, e.g., at the North Atlantic, as in the 1996 version.
See also
References
External links
- Carlos A. Furuti, Map Projections: Polyhedral Maps
- Carlos A. Furuti, All major map projections
- Rotating Waterman as globe Izidor Hafner
- Flat Worlds, Earth Literacy, and Map Alphabetism (Write-up comparing other world maps.)
- Positive News Youth Views site (Waterman selected as their signet.)
