Generalized Beta (GB)
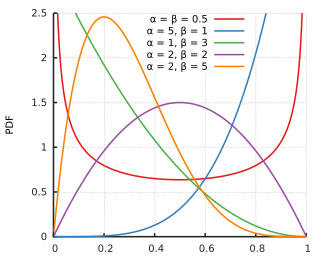
Probability density function
Cumulative distribution function
Parameters
a
{\displaystyle a}
kurtosis ) (real )
b
>
0
{\displaystyle b>0}
scale ) (real )
c
∈
[
0
,
1
]
{\displaystyle c\in [0,1]}
real )
p
>
0
{\displaystyle p>0}
shape ) (real )
q
>
0
{\displaystyle q>0}
shape ) (real ) Support
x
a
∈
(
0
,
b
a
1
−
c
)
{\displaystyle x^{a}\in \left(0,{\frac {b^{a}}{1-c}}\right)}
PDF
|
a
|
x
a
p
−
1
(
1
−
(
1
−
c
)
(
x
/
b
)
a
)
q
−
1
b
a
p
B
(
p
,
q
)
(
1
+
c
(
x
/
b
)
a
)
p
+
q
{\displaystyle {\frac {|a|x^{ap-1}(1-(1-c)(x/b)^{a})^{q-1}}{b^{ap}\mathrm {B} (p,q)(1+c(x/b)^{a})^{p+q}}}}
CDF
no closed form Mean
b
B
(
p
+
1
/
a
,
q
)
B
(
p
,
q
)
2
F
1
[
p
+
1
/
a
1
/
a
p
+
q
+
1
/
a
;
c
]
{\displaystyle {\frac {b\mathrm {B} (p+1/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+1/a&1/a\\p+q+1/a\end{matrix}};c\right]}
hypergeometric series ) Median
no closed form Mode
α
−
1
α
+
β
−
2
{\displaystyle {\frac {\alpha -1}{\alpha +\beta -2}}\!}
α
>
1
,
β
>
1
{\displaystyle \alpha >1,\beta >1}
Variance
b
2
B
(
p
+
2
/
a
,
q
)
B
(
p
,
q
)
2
F
1
[
p
+
2
/
a
2
/
a
p
+
q
+
2
/
a
;
c
]
−
μ
2
{\displaystyle {\frac {b^{2}\mathrm {B} (p+2/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+2/a&2/a\\p+q+2/a\end{matrix}};c\right]-\mu ^{2}}
μ
{\displaystyle \mu }
Skewness
1
σ
3
(
b
3
B
(
p
+
3
/
a
,
q
)
B
(
p
,
q
)
2
F
1
[
p
+
3
/
a
3
/
a
p
+
q
+
3
/
a
;
c
]
−
3
μ
σ
2
−
μ
3
)
{\displaystyle {\frac {1}{\sigma ^{3}}}\left({\frac {b^{3}\mathrm {B} (p+3/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+3/a&3/a\\p+q+3/a\end{matrix}};c\right]-3\mu \sigma ^{2}-\mu ^{3}\right)}
μ
{\displaystyle \mu }
σ
3
{\displaystyle \sigma ^{3}}
Excess kurtosis
see text Entropy
see text MGF
1
+
∑
k
=
1
∞
(
∏
r
=
0
k
−
1
α
+
r
α
+
β
+
r
)
t
k
k
!
{\displaystyle 1+\sum _{k=1}^{\infty }\left(\prod _{r=0}^{k-1}{\frac {\alpha +r}{\alpha +\beta +r}}\right){\frac {t^{k}}{k!}}}
CF
1
F
1
(
α
;
α
+
β
;
i
t
)
{\displaystyle {}_{1}F_{1}(\alpha ;\alpha +\beta ;i\,t)\!}
Confluent hypergeometric function )
In statistics and econometrics , the generalized beta distribution (or GB) is a family of continuous probability distributions of positive random variables with five parameters. The GB distribution includes as special or limiting cases such popular distributions as the beta (both first and second kinds), chi-squared , gamma , F , half-normal , and uniform distributions, among others. The generalized beta distribution allows for considerable flexibility in statistical modeling and testing.
Characterization
Probability density function
The probability density function of the generalized beta distribution is:
f
(
x
;
α
,
β
)
=
|
a
|
x
a
p
−
1
(
1
−
(
1
−
c
)
(
x
/
b
)
a
)
q
−
1
b
a
p
B
(
p
,
q
)
(
1
+
c
(
x
/
b
)
a
)
p
+
q
{\displaystyle {\begin{aligned}f(x;\alpha ,\beta )&={\frac {|a|x^{ap-1}(1-(1-c)(x/b)^{a})^{q-1}}{b^{ap}\mathrm {B} (p,q)(1+c(x/b)^{a})^{p+q}}}\end{aligned}}}
where
B
(
p
,
q
)
{\displaystyle \mathrm {B} (p,q)}
beta function .
A random variable X that is distributed generalized beta with parameters
a
,
b
,
c
,
p
,
q
{\displaystyle a,b,c,p,q}
X
∼
GB
(
a
,
b
,
c
,
p
,
q
)
{\displaystyle X\sim {\textrm {GB}}(a,b,c,p,q)}
Cumulative distribution function
There does not exist a closed-form expression for the cumulative distribution function , so it must be computed numerically . However, the cumulative distribution functions of most of the GB's special cases can be derived analytically. For example, by setting
c
=
0
{\displaystyle c=0}
F
(
x
;
a
,
b
,
c
=
0
,
p
,
q
)
=
2
F
1
[
p
,
1
−
q
;
p
+
1
;
z
]
z
p
p
B
(
p
,
q
)
=
B
z
(
p
,
q
)
{\displaystyle F(x;a,b,c=0,p,q)={\frac {_{2}F_{1}[p,1-q;p+1;z]z^{p}}{p\mathrm {B} (p,q)}}=\mathrm {B} _{z}(p,q)\!}
where
z
=
(
y
b
)
a
{\displaystyle z=({\frac {y}{b}})^{a}}
2
F
1
{\displaystyle _{2}F_{1}}
hypergeometric series , and
B
z
(
p
,
q
)
{\displaystyle \mathrm {B} _{z}(p,q)}
incomplete beta function . Conversely, by setting
c
=
1
{\displaystyle c=1}
F
(
x
;
a
,
b
,
c
=
0
,
p
,
q
)
=
2
F
1
[
p
,
1
−
q
;
p
+
1
;
z
]
z
p
p
B
(
p
,
q
)
=
B
z
(
p
,
q
)
{\displaystyle F(x;a,b,c=0,p,q)={\frac {_{2}F_{1}[p,1-q;p+1;z]z^{p}}{p\mathrm {B} (p,q)}}=\mathrm {B} _{z}(p,q)\!}
where
z
=
(
y
/
b
)
a
1
+
(
y
/
b
)
a
{\displaystyle z={\frac {(y/b)^{a}}{1+(y/b)^{a}}}}
Properties
The mode of a Beta distributed random variable X with parameters α > 1 and β > 1 is:
α
−
1
α
+
β
−
2
{\displaystyle {\begin{aligned}{\frac {\alpha -1}{\alpha +\beta -2}}\\\end{aligned}}}
[ 1] The
k
{\displaystyle k}
X is:
E
[
X
k
]
=
b
k
B
(
p
+
k
/
a
,
q
)
B
(
p
,
q
)
2
F
1
[
p
+
k
/
a
k
/
a
p
+
q
+
k
/
a
;
c
]
{\displaystyle \operatorname {E} [X^{k}]={\frac {b^{k}\mathrm {B} (p+k/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+k/a&k/a\\p+q+k/a\end{matrix}};c\right]}
where
2
F
1
{\displaystyle _{2}F_{1}}
hypergeometric series . Therefore, the expected value (mean) (
μ
{\displaystyle \mu }
variance (second central moment), skewness (third central moment), and kurtosis excess (fourth central moment) of a GB-distributed random variable X are:
μ
=
E
(
X
)
=
b
B
(
p
+
1
/
a
,
q
)
B
(
p
,
q
)
2
F
1
[
p
+
1
/
a
1
/
a
p
+
q
+
1
/
a
;
c
]
{\displaystyle \mu =\operatorname {E} (X)={\frac {b\mathrm {B} (p+1/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+1/a&1/a\\p+q+1/a\end{matrix}};c\right]}
The variance is:
σ
2
=
E
(
X
−
μ
)
2
=
b
2
B
(
p
+
2
/
a
,
q
)
B
(
p
,
q
)
2
F
1
[
p
+
2
/
a
2
/
a
p
+
q
+
2
/
a
;
c
]
−
μ
2
{\displaystyle \sigma ^{2}=\operatorname {E} (X-\mu )^{2}={\frac {b^{2}\mathrm {B} (p+2/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+2/a&2/a\\p+q+2/a\end{matrix}};c\right]-\mu ^{2}}
The skewness is:
γ
1
=
E
(
X
−
μ
)
3
[
E
(
X
−
μ
)
2
]
3
/
2
=
1
σ
3
(
b
3
B
(
p
+
3
/
a
,
q
)
B
(
p
,
q
)
2
F
1
[
p
+
3
/
a
3
/
a
p
+
q
+
3
/
a
;
c
]
−
3
μ
σ
2
−
μ
3
)
{\displaystyle \gamma _{1}={\frac {\operatorname {E} (X-\mu )^{3}}{[\operatorname {E} (X-\mu )^{2}]^{3/2}}}={\frac {1}{\sigma ^{3}}}\left({\frac {b^{3}\mathrm {B} (p+3/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+3/a&3/a\\p+q+3/a\end{matrix}};c\right]-3\mu \sigma ^{2}-\mu ^{3}\right)}
The kurtosis excess is:
γ
2
=
E
(
X
−
μ
)
4
[
E
(
X
−
μ
)
2
]
2
−
3
=
1
σ
4
(
b
4
B
(
p
+
4
/
a
,
q
)
B
(
p
,
q
)
2
F
1
[
p
+
4
/
a
4
/
a
p
+
q
+
4
/
a
;
c
]
−
4
μ
γ
1
σ
3
−
6
μ
2
σ
2
−
μ
4
)
−
3
{\displaystyle \gamma _{2}={\frac {\operatorname {E} (X-\mu )^{4}}{[\operatorname {E} (X-\mu )^{2}]^{2}}}-3={\frac {1}{\sigma ^{4}}}\left({\frac {b^{4}\mathrm {B} (p+4/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+4/a&4/a\\p+q+4/a\end{matrix}};c\right]-4\mu \gamma _{1}\sigma ^{3}-6\mu ^{2}\sigma ^{2}-\mu ^{4}\right)-3}
Given two beta distributed random variables, X ~ Beta(α, β) and Y ~ Beta(α', β'), the differential entropy of X is [ 2]
h
(
X
)
=
ln
B
(
α
,
β
)
−
(
α
−
1
)
ψ
(
α
)
−
(
β
−
1
)
ψ
(
β
)
+
(
α
+
β
−
2
)
ψ
(
α
+
β
)
{\displaystyle {\begin{aligned}h(X)&=\ln \mathrm {B} (\alpha ,\beta )-(\alpha -1)\psi (\alpha )-(\beta -1)\psi (\beta )+(\alpha +\beta -2)\psi (\alpha +\beta )\end{aligned}}}
where
ψ
{\displaystyle \psi }
digamma function .
The cross entropy is
H
(
X
,
Y
)
=
ln
B
(
α
′
,
β
′
)
−
(
α
′
−
1
)
ψ
(
α
)
−
(
β
′
−
1
)
ψ
(
β
)
+
(
α
′
+
β
′
−
2
)
ψ
(
α
+
β
)
.
{\displaystyle H(X,Y)=\ln \mathrm {B} (\alpha ',\beta ')-(\alpha '-1)\psi (\alpha )-(\beta '-1)\psi (\beta )+(\alpha '+\beta '-2)\psi (\alpha +\beta ).\,}
It follows that the Kullback–Leibler divergence between these two beta distributions is
D
K
L
(
X
,
Y
)
=
ln
B
(
α
′
,
β
′
)
B
(
α
,
β
)
−
(
α
′
−
α
)
ψ
(
α
)
−
(
β
′
−
β
)
ψ
(
β
)
+
(
α
′
−
α
+
β
′
−
β
)
ψ
(
α
+
β
)
.
{\displaystyle D_{\mathrm {KL} }(X,Y)=\ln {\frac {\mathrm {B} (\alpha ',\beta ')}{\mathrm {B} (\alpha ,\beta )}}-(\alpha '-\alpha )\psi (\alpha )-(\beta '-\beta )\psi (\beta )+(\alpha '-\alpha +\beta '-\beta )\psi (\alpha +\beta ).}
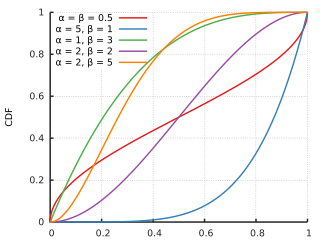
Shapes
The beta density function can take on different shapes depending on the values of the two parameters:
α
=
1
,
β
=
1
{\displaystyle \alpha =1,\ \beta =1}
uniform [0,1] distribution
α
<
1
,
β
<
1
{\displaystyle \alpha <1,\ \beta <1}
α
=
1
2
,
β
=
1
2
{\displaystyle \alpha ={\tfrac {1}{2}},\ \beta ={\tfrac {1}{2}}}
arcsine distribution
α
<
1
,
β
≥
1
{\displaystyle \alpha <1,\ \beta \geq 1}
α
=
1
,
β
>
1
{\displaystyle \alpha =1,\ \beta >1}
α
=
1
,
β
>
2
{\displaystyle \alpha =1,\ \beta >2}
convex
α
=
1
,
β
=
2
{\displaystyle \alpha =1,\ \beta =2}
α
=
1
,
1
<
β
<
2
{\displaystyle \alpha =1,\ 1<\beta <2}
concave
α
=
1
,
β
<
1
{\displaystyle \alpha =1,\ \beta <1}
α
>
1
,
β
≤
1
{\displaystyle \alpha >1,\ \beta \leq 1}
α
>
2
,
β
=
1
{\displaystyle \alpha >2,\ \beta =1}
α
=
2
,
β
=
1
{\displaystyle \alpha =2,\ \beta =1}
1
<
α
<
2
,
β
=
1
{\displaystyle 1<\alpha <2,\ \beta =1}
α
>
1
,
β
>
1
{\displaystyle \alpha >1,\ \beta >1}
unimodal (magenta & cyan plots)Moreover, if
α
=
β
{\displaystyle \alpha =\beta }
Parameter estimation
Let
x
¯
=
1
N
∑
i
=
1
N
x
i
{\displaystyle {\bar {x}}={\frac {1}{N}}\sum _{i=1}^{N}x_{i}}
be the sample mean and
v
=
1
N
−
1
∑
i
=
1
N
(
x
i
−
x
¯
)
2
{\displaystyle v={\frac {1}{N-1}}\sum _{i=1}^{N}(x_{i}-{\bar {x}})^{2}}
be the sample variance . The method-of-moments estimates of the parameters are
α
^
=
x
¯
(
x
¯
(
1
−
x
¯
)
v
−
1
)
,
{\displaystyle {\hat {\alpha }}={\bar {x}}\left({\frac {{\bar {x}}(1-{\bar {x}})}{v}}-1\right),}
β
^
=
(
1
−
x
¯
)
(
x
¯
(
1
−
x
¯
)
v
−
1
)
.
{\displaystyle {\hat {\beta }}=(1-{\bar {x}})\left({\frac {{\bar {x}}(1-{\bar {x}})}{v}}-1\right).}
When the distribution is required over an interval other than [0, 1], say
[
ℓ
,
h
]
{\displaystyle \scriptstyle [\ell ,h]}
x
¯
{\displaystyle {\bar {x}}}
x
¯
−
ℓ
h
−
ℓ
,
{\displaystyle {\frac {{\bar {x}}-\ell }{h-\ell }},}
v
{\displaystyle \ v}
v
(
h
−
ℓ
)
2
{\displaystyle {\frac {v}{(h-\ell )^{2}}}}
[ 3] [ 4]
There is no closed-form of the maximum likelihood estimates for the parameters.
Generating beta-distributed random variates
If
X
{\displaystyle X}
Y
{\displaystyle Y}
X
∼
Γ
(
α
,
θ
)
{\displaystyle X\sim {\rm {\Gamma }}(\alpha ,\theta )\,}
Y
∼
Γ
(
β
,
θ
)
{\displaystyle Y\sim {\rm {\Gamma }}(\beta ,\theta )\,}
X
X
+
Y
∼
B
e
t
a
(
α
,
β
)
{\displaystyle {\tfrac {X}{X+Y}}\sim {\rm {Beta}}(\alpha ,\beta )\,}
X /(X+Y ), where X is a gamma variate with parameters (
α
,
1
{\displaystyle \alpha ,1}
Y is an independent gamma variate with parameters (
β
,
1
{\displaystyle \beta ,1}
[ 5]
Also, the k th order statistic of
n
{\displaystyle n}
uniformly distributed variates is
B
e
t
a
(
k
,
n
+
1
−
k
)
{\displaystyle {\rm {Beta}}(k,n+1-k)}
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
α
+
β
−
1
{\displaystyle \alpha +\beta -1}
α
{\displaystyle \alpha }
[ 6]
If
X
∼
B
e
t
a
(
a
,
b
)
{\displaystyle X\sim {\rm {Beta}}(a,b)\,}
1
−
X
∼
B
e
t
a
(
b
,
a
)
{\displaystyle 1-X\sim {\rm {Beta}}(b,a)\,}
If
X
∼
B
e
t
a
(
a
,
b
)
{\displaystyle X\sim {\rm {Beta}}(a,b)\,}
X
1
−
X
∼
B
e
t
a
P
r
i
m
e
(
a
,
b
)
{\displaystyle {\tfrac {X}{1-X}}\sim {\rm {BetaPrime}}(a,b)\,}
beta prime distribution , also called "beta distribution of the second kind".
If
X
∼
B
e
t
a
(
n
2
,
m
2
)
{\displaystyle X\sim {\rm {Beta}}({\tfrac {n}{2}},{\tfrac {m}{2}})\,}
m
X
n
(
1
−
X
)
∼
F
(
n
,
m
)
{\displaystyle {\tfrac {mX}{n(1-X)}}\sim F(n,m)}
If
X
∼
B
e
t
a
(
1
+
λ
c
−
m
i
n
m
a
x
−
m
i
n
,
1
+
λ
m
a
x
−
c
m
a
x
−
m
i
n
)
{\displaystyle X\sim {\rm {Beta}}\left(1+\lambda {\tfrac {c-min}{max-min}},1+\lambda {\tfrac {max-c}{max-min}}\right)\!\!\,}
m
i
n
+
X
(
m
a
x
−
m
i
n
)
∼
P
E
R
T
(
m
i
n
,
m
a
x
,
c
,
λ
)
,
{\displaystyle \!\!min+X(max-min)\sim PERT(min,max,c,\lambda )\,,}
PERT denotes a distribution used in PERT analysis.[citation needed
If
X
∼
B
e
t
a
(
1
,
β
)
{\displaystyle X\sim {\rm {Beta}}(1,\beta )\,}
X
∼
{\displaystyle X\sim \,}
Kumaraswamy distribution with parameters
(
1
,
β
)
{\displaystyle (1,\beta )\,}
If
X
∼
B
e
t
a
(
α
,
1
)
{\displaystyle X\sim {\rm {Beta}}(\alpha ,1)\,}
X
∼
{\displaystyle X\sim \,}
Kumaraswamy distribution with parameters
(
α
,
1
)
{\displaystyle (\alpha ,1)\,}
If
X
∼
B
e
t
a
(
α
,
1
)
{\displaystyle X\sim {\rm {Beta}}(\alpha ,1)\,}
−
l
n
(
X
)
∼
Exponential
(
α
)
{\displaystyle -ln(X)\sim {\textrm {Exponential}}(\alpha )\,}
Special and limiting cases
B
e
t
a
(
1
,
1
)
∼
U
(
0
,
1
)
{\displaystyle {\rm {Beta}}(1,1)\sim {\rm {U}}(0,1)\,}
uniform distribution .If
X
∼
B
e
t
a
(
3
2
,
3
2
)
{\displaystyle X\sim {\rm {Beta}}({\tfrac {3}{2}},{\tfrac {3}{2}})\,}
r
>
0
{\displaystyle r>0\,}
2
r
X
−
r
∼
{\displaystyle 2rX-r\sim \,}
Wigner semicircle distribution .
B
e
t
a
(
1
2
,
1
2
)
{\displaystyle {\rm {Beta}}({\tfrac {1}{2}},{\tfrac {1}{2}})\ }
Jeffreys prior for a proportion and is equivalent to arcsine distribution .
lim
n
→
∞
n
B
e
t
a
(
1
,
n
)
=
E
x
p
(
1
)
{\displaystyle \lim _{n\to \infty }n{\rm {Beta}}(1,n)={\rm {Exp}}(1)\,}
exponential distribution
lim
n
→
∞
n
B
e
t
a
(
k
,
n
)
=
Gamma
(
k
,
1
)
{\displaystyle \lim _{n\to \infty }n{\rm {Beta}}(k,n)={\textrm {Gamma}}(k,1)\,}
gamma distribution
Derived from other distributions
The k th order statistic of a sample of size n from the uniform distribution is a beta random variable,
U
(
k
)
∼
B
(
k
,
n
+
1
−
k
)
.
{\displaystyle U_{(k)}\sim B(k,n+1-k).}
[ 6]
If
X
∼
Γ
(
α
,
θ
)
{\displaystyle X\sim {\rm {\Gamma }}(\alpha ,\theta )\,}
Y
∼
Γ
(
β
,
θ
)
{\displaystyle Y\sim {\rm {\Gamma }}(\beta ,\theta )\,}
X
X
+
Y
∼
B
e
t
a
(
α
,
β
)
{\displaystyle {\tfrac {X}{X+Y}}\sim {\rm {Beta}}(\alpha ,\beta )\,}
If
X
∼
χ
2
(
α
)
{\displaystyle X\sim \chi ^{2}(\alpha )\,}
Y
∼
χ
2
(
β
)
{\displaystyle Y\sim \chi ^{2}(\beta )\,}
X
X
+
Y
∼
B
e
t
a
(
α
2
,
β
2
)
{\displaystyle {\tfrac {X}{X+Y}}\sim {\rm {Beta}}({\tfrac {\alpha }{2}},{\tfrac {\beta }{2}})\,}
If
X
∼
Unif
(
0
,
1
)
{\displaystyle X\sim \operatorname {Unif} (0,1)}
α
>
0
{\displaystyle \alpha \,>0}
X
1
α
∼
Beta
(
α
,
1
)
{\displaystyle X^{\frac {1}{\alpha }}\sim \operatorname {Beta} (\alpha ,1)}
If
X
∼
U
(
0
,
1
]
{\displaystyle X\sim {\rm {U}}(0,1]\,}
X
2
∼
B
e
t
a
(
1
2
,
1
)
{\displaystyle X^{2}\sim {\rm {Beta}}({\tfrac {1}{2}},1)\ }
power-function distribution .[clarification needed
Combination with other distributions
X
∼
B
e
t
a
(
α
,
β
)
{\displaystyle X\sim {\rm {Beta}}(\alpha ,\beta )\,}
Y
∼
F
(
2
α
,
2
β
)
{\displaystyle Y\sim F(2\alpha ,2\beta )\,}
Pr
(
X
≤
α
α
+
β
x
)
=
Pr
(
Y
≥
x
)
{\displaystyle \Pr(X\leq {\tfrac {\alpha }{\alpha +\beta x}})=\Pr(Y\geq x)\,}
x > 0.
Compounding with other distributions
If
p
∼
B
e
t
a
(
α
,
β
)
{\displaystyle p\sim \mathrm {Beta} (\alpha ,\beta )\,}
X
∼
Bin
(
k
,
p
)
{\displaystyle X\sim \operatorname {Bin} (k,p)\,}
X
∼
{\displaystyle X\sim \,}
beta-binomial distribution
If
p
∼
B
e
t
a
(
α
,
β
)
{\displaystyle p\sim \mathrm {Beta} (\alpha ,\beta )\,}
X
∼
NB
(
r
,
p
)
{\displaystyle X\sim \operatorname {NB} (r,p)\,}
X
∼
{\displaystyle X\sim \,}
beta negative binomial distribution
Generalisations
The Dirichlet distribution is a multivariate generalization of the beta distribution. Univariate marginals of the Dirichlet distribution have a beta distribution.
The beta distribution is a special case of the Pearson type I distribution
B
e
t
a
(
α
,
β
)
=
lim
δ
→
0
N
o
n
C
e
n
t
r
a
l
B
e
t
a
(
α
,
β
,
δ
)
{\displaystyle {\rm {Beta}}(\alpha ,\beta )=\lim _{\delta \to 0}{\rm {NonCentralBeta}}(\alpha ,\beta ,\delta )\,}
noncentral beta distribution
Other
Applications
Order statistics
The beta distribution has an important application in the theory of order statistics . A basic result is that the distribution of the k'th largest of a sample of size n from a continuous uniform distribution has a beta distribution.[ 6]
U
(
k
)
∼
B
(
k
,
n
+
1
−
k
)
.
{\displaystyle U_{(k)}\sim B(k,n+1-k).}
From this, and application of the theory related to the probability integral transform , the distribution of any individual order statistic from any continuous distribution can be derived.[ 6]
Rule of succession
A classic application of the beta distribution is the rule of succession , introduced in the 18th century by Pierre-Simon Laplace in the course of treating the sunrise problem . It states that, given s successes in n conditionally independent Bernoulli trials with probability p, that p should be estimated as
s
+
1
n
+
2
{\displaystyle {\frac {s+1}{n+2}}}
p, namely Beta(s + 1, n − s + 1), which is given by Bayes' rule if one assumes a uniform prior over p (i.e., Beta(1, 1)) and then observes that p generated s successes in n trials.
Bayesian inference
Beta distributions are used extensively in Bayesian inference , since beta distributions provide a family of conjugate prior distributions for binomial (including Bernoulli ) and geometric distributions . The Beta(0,0) distribution is an improper prior and sometimes used to represent ignorance of parameter values.
The domain of the beta distribution can be viewed as a probability, and in fact the beta distribution is often used to describe the distribution of an unknown probability value — typically, as the prior distribution over a probability parameter, such as the probability of success in a binomial distribution or Bernoulli distribution . In fact, the beta distribution is the conjugate prior of the binomial distribution and Bernoulli distribution .
The beta distribution is the special case of the Dirichlet distribution with only two parameters, and the beta is conjugate to the binomial and Bernoulli distributions in exactly the same way as the Dirichlet distribution is conjugate to the multinomial distribution and categorical distribution .
In Bayesian inference, the beta distribution can be derived as the posterior probability of the parameter p of a binomial distribution
after observing α − 1 successes (with probability p of success) and β − 1 failures (with probability 1 − p of failure). Another way to express this is that placing a prior distribution of Beta(α,β) on the parameter p of a binomial distribution is equivalent to adding α pseudo-observations of "success" and β pseudo-observations of "failure" to the actual number of successes and failures observed, then estimating the parameter p by the proportion of successes over both real- and pseudo-observations. If α and β are greater than 0, this has the effect of smoothing out the distribution of the parameters by ensuring that some positive probability mass is assigned to all parameters even when no actual observations corresponding to those parameters is observed. Values of α and β less than 1 favor sparsity, i.e. distributions where the parameter p is close to either 0 or 1. In effect, α and β, when operating together, function as a concentration parameter ; see that article for more details.
Task duration modeling
The beta distribution can be used to model events which are constrained to take place within an interval defined by a minimum and maximum value. For this reason, the beta distribution — along with the triangular distribution — is used extensively in PERT , critical path method (CPM) and other project management / control systems to describe the time to completion of a task. In project management, shorthand computations are widely used to estimate the mean and standard deviation of the beta distribution:
μ
(
X
)
=
a
+
4
b
+
c
6
σ
(
X
)
=
c
−
a
6
{\displaystyle {\begin{aligned}\mu (X)&{}={\frac {a+4b+c}{6}}\\\sigma (X)&{}={\frac {c-a}{6}}\end{aligned}}}
where a is the minimum, c is the maximum, and b is the most likely value.
Using this set of approximations is known as three-point estimation and are exact only for particular values of α and β, specifically when[ 7]
α
=
3
−
2
{\displaystyle \alpha =3-{\sqrt {2}}\,}
β
=
3
+
2
{\displaystyle \beta =3+{\sqrt {2}}\,}
or vice versa.
These are notably poor approximations for most other beta distributions exhibiting average errors of 40% in the mean and 549% in the variance[ 8] [ 9] [ 10]
Alternative parameterizations
Mean and sample size
The beta distribution may also be reparameterized in terms of its mean μ (0 ≤ μ ≤ 1) and sample size ν = α + β (ν > 0). This is useful in Bayesian parameter estimation if one wants to place an unbiased (uniform) prior over the mean. For example, one may administer a test to a number of individuals. If it is assumed that each person's score (0 ≤ θ ≤ 1) is drawn from a population-level Beta distribution, then an important statistic is the mean of this population-level distribution. The mean and sample size parameters are related to the shape parameters α and β via[ 11]
α
=
μ
ν
,
β
=
(
1
−
μ
)
ν
.
{\displaystyle {\begin{aligned}\alpha &{}=\mu \nu ,\\\beta &{}=(1-\mu )\nu .\end{aligned}}}
Under this parameterization, one can place a uniform prior over the mean, and a vague prior (such as an exponential or gamma distribution) over the positive reals for the sample size.
The Balding–Nichols model is a similar two-parameter reparameterization of the beta distribution.
Four parameters
A beta distribution with the two shape parameters α and β is supported on the range [0,1]. It is possible to alter the location and scale of the distribution by introducing two further parameters representing the minimum and maximum values of the distribution.[ 12]
The probability density function of the four parameter beta distribution is given by
f
(
y
;
α
,
β
,
a
,
b
)
=
1
B
(
α
,
β
)
(
y
−
a
)
α
−
1
(
b
−
y
)
β
−
1
(
b
−
a
)
α
+
β
−
1
.
{\displaystyle f(y;\alpha ,\beta ,a,b)={\frac {1}{B(\alpha ,\beta )}}{\frac {(y-a)^{\alpha -1}(b-y)^{\beta -1}}{(b-a)^{\alpha +\beta -1}}}.}
The mean, mode and variance of the four parameters Beta distribution are:
mean
=
α
b
+
β
a
α
+
β
{\displaystyle {\text{mean}}={\frac {\alpha b+\beta a}{\alpha +\beta }}\ }
mode
=
(
α
−
1
)
b
+
(
β
−
1
)
a
α
+
β
−
2
for
α
>
1
,
β
>
1
{\displaystyle {\text{mode}}={\frac {(\alpha -1)b+(\beta -1)a}{\alpha +\beta -2}}\qquad {\text{for}}\ \alpha >1,\beta >1\ }
variance
=
α
β
(
b
−
a
)
2
(
α
+
β
)
2
(
α
+
β
+
1
)
{\displaystyle {\text{variance}}={\frac {\alpha \beta (b-a)^{2}}{(\alpha +\beta )^{2}(\alpha +\beta +1)}}\ }
The standard form can be obtained by letting
x
=
y
−
a
b
−
a
.
{\displaystyle x={\frac {y-a}{b-a}}.}
References
^ Johnson, Norman L., Samuel Kotz, and N. Balakrishnan (1995). "Continuous Univariate Distributions, Vol. 2", Wiley, ISBN 978-0471584940.
^ A. C. G. Verdugo Lazo and P. N. Rathie. "On the entropy of continuous probability distributions," IEEE Trans. Inf. Theory, IT-24:120–122,1978.
^ Engineering Statistics Handbook ^ Brighton Webs Ltd. Data & Analysis Services for Industry & Education ^ van der Waerden, B. L., "Mathematical Statistics", Springer, ISBN 978-3540045076.
^ a b c d David, H. A., Nagaraja, H. N. (2003) Order Statistics (3rd Edition). Wiley, New Jersey pp 458. ISBN 0-471-38926-9
^ Grubbs, Frank E. (1962). Attempts to Validate Certain PERT Statistics or ‘Picking on PERT’. Operations Research 10(6), p. 912–915.
^ Keefer, Donald L. and Verdini, William A. (1993). Better Estimation of PERT Activity Time Parameters. Management Science 39(9), p. 1086–1091.
^ Keefer, Donald L. and Bodily, Samuel E. (1983). Three-point Approximations for Continuous Random variables. Management Science 29(5), p. 595–609.
^ DRMI Newsletter, Issue 12, April 8, 2005 ^ Kruschke, J. (2011). Doing Bayesian data analysis: A tutorial with R and BUGS. Academic Press / Elsevier, p. 83.
^ Beta4 distribution
External links
Discrete
with finite with infinite
Continuous
supported on a supported on a supported with support
Mixed
Multivariate Directional Degenerate singular Families
Template:Common univariate probability distributions



![{\displaystyle c\in [0,1]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/02b2796dc5e3cb6527d1ac6e766dc1da2ef1e120)




![{\displaystyle {\frac {b\mathrm {B} (p+1/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+1/a&1/a\\p+q+1/a\end{matrix}};c\right]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/bf0880bbd6917723101a396f55c1729ae947fcbe)


![{\displaystyle {\frac {b^{2}\mathrm {B} (p+2/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+2/a&2/a\\p+q+2/a\end{matrix}};c\right]-\mu ^{2}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/015dbc06e3b63704714939a79efd497ba0b1b755)

![{\displaystyle {\frac {1}{\sigma ^{3}}}\left({\frac {b^{3}\mathrm {B} (p+3/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+3/a&3/a\\p+q+3/a\end{matrix}};c\right]-3\mu \sigma ^{2}-\mu ^{3}\right)}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/a8a17a162ddc403feaa7d2ad95d2739c43780e3a)








![{\displaystyle F(x;a,b,c=0,p,q)={\frac {_{2}F_{1}[p,1-q;p+1;z]z^{p}}{p\mathrm {B} (p,q)}}=\mathrm {B} _{z}(p,q)\!}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/78412e48011b6ac5f7727db7d9856bf78d971aad)







![{\displaystyle \operatorname {E} [X^{k}]={\frac {b^{k}\mathrm {B} (p+k/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+k/a&k/a\\p+q+k/a\end{matrix}};c\right]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/65fc13de0a8506b4ad1082b8152070d28e37883e)
![{\displaystyle \mu =\operatorname {E} (X)={\frac {b\mathrm {B} (p+1/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+1/a&1/a\\p+q+1/a\end{matrix}};c\right]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/b641e77bce65be0fca1af55dee5c8c13c1600e77)
![{\displaystyle \sigma ^{2}=\operatorname {E} (X-\mu )^{2}={\frac {b^{2}\mathrm {B} (p+2/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+2/a&2/a\\p+q+2/a\end{matrix}};c\right]-\mu ^{2}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/974f1468e4195f1a4dea21870412f5736d40fe49)
![{\displaystyle \gamma _{1}={\frac {\operatorname {E} (X-\mu )^{3}}{[\operatorname {E} (X-\mu )^{2}]^{3/2}}}={\frac {1}{\sigma ^{3}}}\left({\frac {b^{3}\mathrm {B} (p+3/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+3/a&3/a\\p+q+3/a\end{matrix}};c\right]-3\mu \sigma ^{2}-\mu ^{3}\right)}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/68759aaffbd4d468b8c9d174287c78d4b48a2e94)
![{\displaystyle \gamma _{2}={\frac {\operatorname {E} (X-\mu )^{4}}{[\operatorname {E} (X-\mu )^{2}]^{2}}}-3={\frac {1}{\sigma ^{4}}}\left({\frac {b^{4}\mathrm {B} (p+4/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+4/a&4/a\\p+q+4/a\end{matrix}};c\right]-4\mu \gamma _{1}\sigma ^{3}-6\mu ^{2}\sigma ^{2}-\mu ^{4}\right)-3}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/5062b8add2ae7c6d29a6ab7fea6ca92feb1355fc)























![{\displaystyle \scriptstyle [\ell ,h]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/bcc4e5aba23f2120854fa2229d97dba92c7ca2c4)











































![{\displaystyle X\sim {\rm {U}}(0,1]\,}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/de74bb323a07dccdd103dfd537ce9f9b85d0d5ce)

















