Talk:Nusselt number
| Physics: Fluid Dynamics C‑class Mid‑importance | |||||||||||||
| |||||||||||||
Derivation
This newly added sub topic is seriously lacking in material, explanation and is of questionable accuracy... any suggestions?
Characteristic Length
I have went through some research papers. The equation h=K * Nu /L, all the research papers are saying, L is the characteristic length. But they did not give any equation to relate that characteristics length with geometry of the convection surfaces.
In one research paper L is considered as diameter. Then, how can we calculate nusselt number for a flat plate?????????
The characteristic length depends on the geometry.
For a circular pipe the characteristic length would be the diameter.
For non circular ducts, the characteristic length would be:
L=4A/p
where A is the cross-sectional area of the duct, P would be the wetted perimeter.
Note that for a circular pipe:
L=4*(pi*D^2/4)/(pi*D) = D
For flat plates, the characteristic length is usually the distance from the leading edge for a local Nusselt number. Average Nusselt numbers over a distance 0 to L use the L as the characteristic length. Note that most of these Nusselt number relationships (based on Reynolds and Prandlt numbers) are empirical.
- As above, Nu will in general depend on the geometry under consideration. Selection of the significant length dimension will obviously change the value of Nu. I cannot say for certain as I am not a professor of fluid mechanics (merely a mechanical engineering undergrad), but I believe that the selection of the significant length dimension should be the direction of the growth of the boundary layer. An example would be that of a horizontal cylinder and a vertical cylinder in natural convection. For the vertical cylinder, the significant length dimension is the height L. For the horizontal cylinder, the significant length dimension is the diameter D.
- I just got an e-mail back from the TA for my heat transfer class. He confirmed that the above is correct, so I'll be updating the Nusselt Number main page.
Nusselt number vs Biot number
Could someone explain what the difference between the Nusselt number and the Biot number is? They have very similar expressions.
- The Nusselt number is most useful in determining the convective heat transfer coefficient, whereas the Biot number is used in unsteady problems.
- This is a typical exam question. The "k" in the Biot numer is of a solid, that in the Nusselt number of a fluid. Different meaning, different use... see a heat transfer textbook.
how to calculate nusselt no.
For finding heat loss in natural convection we require heat transfer coefficeint(h). For finding h we require nusselt no. Now how to calculate nusselt no. There are different equations for different cases.
in perpendicular
maybe the "in perpendicular to the flow direction" should be rephrased or something?
Ratio of convection to conduction transfer
This equality is far too general to be of any help. For instance, in natural convection in cavities is literal, in laminar internal flows can be descriptive of the situation and in turbulent and external flows is simply false. To explain fully what it means would require several pages. In addition, it tends to confuse students. For instance, they then mix-up Nusselt and Biot numbers, since the ratio is much more meaningful for the latter.
Xtobal (talk) 12:02, 14 April 2008 (UTC)
- Fair enough. I have no problem with you removing that part of the equation now that you have explained that, but before it appeared more like vandalism because there was no explanation to why it was deleted. In the future I recommend that you used the edit summary. Thanks! --Wizard191 (talk) 12:55, 14 April 2008 (UTC)
I would like to add that I think the definition is still somewhat poor and could lead to the same confusion as mentioned above. The fact that the Nusselt number ends up being equal to the ratio of convective to conductive heat transfer in a fluid is a result of its formulation, not what it actually represents. Physically, the Nusselt number is actually the dimensionless temperature gradient at an interface. When this is applied to a convection interface you obtain the typical ratio as shown, which is what the Nusselt number equates to, not what it "is". I would like to see this better explained in here. More details can be found in intermediate heat transfer texts, including the free textbook "A Heat Transfer Textbook" by Linehard and Linehard. —Preceding unsigned comment added by 24.118.49.238 (talk) 13:37, 13 November 2008 (UTC)
Nu = f(Ra, Pr)
I guess you can say that (for natural convection) Nu is function of Ra & Pr but Ra = Pr*Gr. So isn't it more logical to just say Nu = f(Ra) or Nu = f(Gr,Pr). (and Nu = f(Re,Pr) for forced convection) —Preceding unsigned comment added by 134.184.120.160 (talk) 12:41, 17 August 2008 (UTC)
references
Why are there citations for 3 editions of the same book...164.54.53.85 (talk) 19:40, 19 March 2010 (UTC)
- Because people added content from three different editions so it must be noted. I know I have one of those editions, but I couldn't say I had it from one of the other editions referenced, therefore the three are noted. Wizard191 (talk) 20:59, 19 March 2010 (UTC)
Wrong definition ?
The definition for the Nusselt number as ratio of convective heat transfer over conductive heat transfer seems to be wrong, because it's the definition of the Peclet number (forced convection) or Rayleigh number (free convection). The correct definition is total heat transfer over conductive heat transfer. This implies that convection is not including conduction and is completely different. — Preceding unsigned comment added by Biglama (talk • contribs) 21:54, 10 December 2011 (UTC)
- The term convection is somewhat ambiguous, since it is sometimes used as a synonym for advection, what seems to be your definition. I clarified that it includes both advection and conduction, which is also the primary definition in the convection article. Total heat transfer would also include radiative heat transfer and that is definitely incorrect. Han-Kwang (t) 09:49, 11 December 2011 (UTC)
- Thank you for the accurate information especially about advection and yes my definition of convection was the definition of advection. Just a small question: why the total heat tranfer couldn't be used in the nusselt number definition ? There are some mathematical formulations which allow to define the radiative heat transfer as a linear function of temperature difference.
- If dT is small, it is possible to describe the radiative equation q = 4*σ*A*ε*(T14-T24) as Taylors series to get q = 4*σ*A*ε*T23(T1-T2) Biglama (talk) 12:40, 30 March 2012 (UTC)
- I am not an expert but I had a lecture during my studies which provide a global overview of transport phenomena:

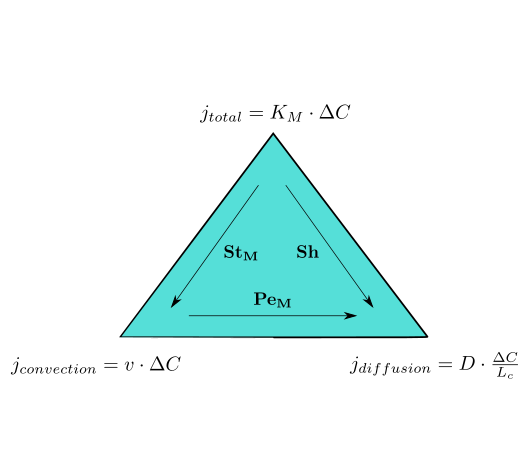
- Biglama (talk) 12:55, 30 March 2012 (UTC)
Confusing introduction
'In this context, convection includes both advection and conduction.' How can convection include conduction?! | Moemin05 (talk) 16:49, 29 March 2012 (UTC)
- It is a huge mess: some books consider that convection refers only to natural or free convection, others which define convection as advection+conduction and some as synonym of advection. The definition change in the past several times and all modern books are not using the same definition Biglama (talk) 12:45, 30 March 2012 (UTC)

