Covariant transformation

See also Covariance and contravariance of vectors

Co/Contra-variant Transformations

The co/contra-variant nature of vector coordinates has been treated as an elementary characterisation in Tensor Analysis. For example in the classic text translated from the Russian 1966 3rd Edition and published by Dover, the coordinate space is first introduced with coordinates in superscript indices (xⁱ) and oblique reference frame and basis vectors with subscript indices ($\mathbf {e} _{i}={\frac {\partial }{\partial {x}^{i}}}$); and the motivation for this convention is deferred to following text quoted later:

"These designations of the components of a vector stem from the fact that the direct transformation of the covariant components involves the coefficients α^k_i' of the direct transformation, that is A'_i= α^k_i'A_k. while the direct transformation of the contravariant components involve the coefficients α^i'_k of the inverse transformation A'ⁱ = α^i'_kA^k."

In the first instance, suppose f is a function over vector space, one can express the scalar derivative components of f in new coordinates in terms of the old coordinates using the chain rule and get

${\frac {\partial f}{\partial {x'}^{i}}}=\sum _{j}{\frac {\partial {x}^{j}}{\partial {x'}^{i}}}{\frac {\partial f}{\partial {x}^{j}}}.\;$

Direct differentiation of the coordinate values produces a transformation with each k-i element $\alpha _{i'}^{k}={\frac {\partial {x}^{k}}{\partial {x'}^{i}}}$, where the transformed (new) bases equal the rate of change of the old (x) bases with respect to the new (x') coordinates, times the old bases. To paraphrase, transforms as change of old bases times the old, (transform directly, component index in subscript).

In the second case where the components are not coordinates but some derivative of the coordinate such that vⁱ = dxⁱ/dλ, when we perform a change of bases, for each new coordinate component (i), xⁱ, it fixes relative to independent scalar components (j), by the chain rule

$v'^{i}={\frac {dx'^{i}}{dx^{j}}}{\frac {dx^{j}}{d\lambda }}={\frac {\partial x'^{i}}{\partial x^{j}}}v^{j},$

namely $\alpha _{k}^{i'}={\frac {\partial x'^{i}}{\partial x^{j}}}$, that the new bases equal the rate of change of the new (x') coordinates with respect to the old (x) coordinates, times the old bases. To paraphrase, transforms as change of new bases times the old (transform inversely, component index in superscript).

Algebraic Characterisation

The co/contra-variance of a transformation is an algebraic property, and the designation cited above also applies in a generalised differential geometry setting where givan a category C and vector spaces V, W belonging to C, a covariant functor L maps the set of homomorphisms Hom(V,W) to Hom(LV,LW), whereas a contravariant functor L' maps Hom(V,W) to Hom(L'W,L'V). Again notice the transformation domain's push forward direction in the covariant, and pull-back direction in the contravariant case. This construct extends the covariant differential to manifolds such as vector bundles and their connections, for example by parallel transport extending covariant derivatives to vector fields over manifolds by affinely connecting tangent vectors from one tangent bundle on the manifold to neighbouring fibres along a 'curve' (see for example covariant derivative).

The diagram following illustrates one such curve across three manifolds, from around the cone in conical chart X, then around the cylinder through cylindrical chart X' and finally along the rectilinear plane through rectangular chart X". The tangent vector representing a force along its transmission path, that is along the curve, is preserved by parallel transport, barring friction loss or geometric distortion of medium.

Displacement of force vectors through change of coordinates from Conical coordinates X to Cylindrical coordinates X′ and Rectangular coordinates X″, by Parallel transport firstly of torques $\omega _{z}$, $\omega _{x}$ in coincident parallel planes along coordinate system overlap connection line (zx) and consequently to force f_y along coordinate system overlap connection line (yx) respectively. The force / torque vector (magnitude and direction) at each connection point is invariant of coordinates.

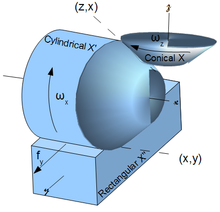
Invariance

Metric Invariance is a geometric concept indicating how a physical property does not change with arbitrary coordinate frames. For example, in (early) tensor analysis elasticity, namely Young's Modulus, should not change simply because we measure it with tensile testing of a rectangular object (a bar) or cylindrical one (a rod). Invariance refers to the fact that elasticity is an independent physical property which is only recovered through the determinant of stress/strain tensors – (summation over all indices), irrespective whether in cylindrical or rectangular coordinates and the transform and its adjoint commute.

Other references to invariance exist – of say parallelism structures on fibre bundles where the covariant derivative can be recovered unchanged across bundle charts under parallel transport.

In an earlier (1931) work referring to Invariance, the term is given as an attribute of scalar or vector quantities of physical or geometric nature that should remain unchanged with change of coordinate system. Even more instructive in that work is the teaching that Invariance precedes the co/contra-variant transformation relational property; viz: "Predetermination of the invariance of certain quantities is a basic aid in the development of (their) transformation theory.".

Examples of geometric or physical invariants given in the work cited, include:

"The magnitude of a fixed vector, the scalar products of two and three fixed vectors, the divergence of a fixed vector, the work done by a force in a displacement, and the energy stored per unit volume in a strained elastic medium are examples of scalar invariants. In addition to the fixed vector, the vector product of two or three fixed vectors, the gradient of a scalar function, and the curl of a vector point function are examples of vector invariants."

The subsequent transformation theory developed in the cited work reduces to the following simple rules:

"Reciprocal differentials and the unitary vectors are said to transform 'co-gradiently'; on the other hand the differentials of coordinates and reciprocal unitary vectors transform 'contra-gradiently'; that the first pair vary contra-gradiently to the former pair; and finally that the former set are referred to as Covariant Quantities, and the latter as Contravariant Quantities.".

It may be noted here that the co/contra-gradient transform terminology has since been abandoned in contemporary discourse, in favour of the co/contra-variant quantity terminology, irrespective of whether addressing quantity or transform.

Covariant Transformation

In physics, a covariant transformation is a rule (specified below), that describes how certain physical entities change under a change of coordinate system. In particular the term is used for vectors and tensors. The transformation that describes the new basis vectors in terms of the old basis, is defined as a covariant transformation. Conventionally, indices identifying the basis vectors are placed as lower indices and so are all entities that transform in the same way. The inverse of a covariant transformation is a contravariant transformation. In order that a vector should be invariant under a coordinate transformation, its components must transform according to the contravariant rule. Conventionally, indices identifying the components of a vector are placed as upper indices and so are all indices of entities that transform in the same way. The summation over all indices of a product with the same lower and upper indices are invariant to a transformation.

A vector itself is a geometrical quantity, in principle, independent (invariant) of the chosen coordinate system. A vector v is given, say, in components vⁱ on a chosen basis e_i, related to a coordinate system xⁱ (the basis vectors are tangent vectors to the coordinate grid). On another basis, say ${\mathbf {e} }'_{i}$, related to a new coordinate system $x'^{i}$, the same vector v has different components $v'^{i}$ and

${\mathbf {v} }=\sum _{i}v^{i}{\mathbf {e} }_{i}=\sum _{i}{v'}^{i}{\mathbf {e} }'_{i}$

(in the so called Einstein notation the summation sign is often omitted, implying summation over the same upper and lower indices occurring in a product). With v as invariant and the ${\mathbf {e} }_{i}$ transforming covariant, it must be that the $v^{i}$ (the set of numbers identifying the components) transform in a different way, the inverse called the contravariant transformation rule.

If, for example in a 2-dim Euclidean space, the new basis vectors are rotated anti-clockwise with respect to the old basis vectors, then it will appear in terms of the new system that the componentwise representation of the vector look as if the vector was rotated in the opposite direction, i.e. clockwise (see figure).

---

• 
  A vector v, and local tangent basis vectors {e_x,e_y} and {e_r,e_φ}.
• 
  Coordinate representations of v.

A vector v is described in a given coordinate grid (black lines) on a basis which are the tangent vectors to the (here rectangular) coordinate grid. The basis vectors are e_x and e_y. In another coordinate system (dashed and red), the new basis vectors are tangent vectors in the radial direction and perpendicular to it. These basis vectors are indicated in red as e_r and e_φ. They appear rotated anticlockwise with respect to the first basis. The covariant transformation here is thus an anticlockwise rotation.

If we view the vector v with e_φ pointed upwards, its representation in this frame appears rotated to the right. The contravariant transformation is a clockwise rotation.
.

---

Examples of covariant transformation

The derivative of a function transforms covariantly

The explicit form of a covariant transformation is best introduced with the transformation properties of the derivative of a function. Consider a scalar function f (like the temperature in a space) defined on a set of points p, identifiable in a given coordinate system $x^{i},\;i=0,1,\dots$ (such a collection is called a manifold). If we adopt a new coordinates system ${x'}^{j},j=0,1,\dots$ then for each i, the original coordinate ${x}^{i}$ can be expressed as function of the new system, so ${x}^{i}({x'}^{j}),j=0,1,\dots$ One can express the derivative of f in new coordinates in terms of the old coordinates, using the chain rule of the derivative, as

${\frac {\partial f}{\partial {x'}^{i}}}=\sum _{j}{\frac {\partial f}{\partial {x}^{j}}}\;{\frac {\partial {x}^{j}}{\partial {x'}^{i}}}$

This is the explicit form of the covariant transformation rule. The notation of a normal derivative with respect to the coordinates sometimes uses a comma, as follows

$f_{,i}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\partial f}{\partial x^{i}}}$

where the index i is placed as a lower index, because of the covariant transformation.

Basis vectors transform covariantly

A vector can be expressed in terms of basis vectors. For a certain coordinate system, we can choose the vectors tangent to the coordinate grid. This basis is called the coordinate basis.

To illustrate the transformation properties, consider again the set of points p, identifiable in a given coordinate system $x^{i}$ where $i=0,1,\dots$ (manifold). A scalar function f, that assigns a real number to every point p in this space, is a function of the coordinates $f\;(x^{0},x^{1},\dots )$. A curve is a one-parameter collection of points c, say with curve parameter λ, c(λ). A tangent vector v to the curve is the derivative $dc/d\lambda$ along the curve with the derivative taken at the point p under consideration. Note that we can see the tangent vector v as an operator (the Directional derivative) which can be applied to a function

${\mathbf {v} }[f]\ {\stackrel {\mathrm {def} }{=}}\ {\frac {df}{d\lambda }}={\frac {d\;\;}{d\lambda }}f(c(\lambda ))$

The parallel between the tangent vector and the operator can also be worked out in coordinates

${\mathbf {v} }[f]=\sum _{i}{\frac {dx^{i}}{d\lambda }}{\frac {\partial f}{\partial x^{i}}}$

or in terms of operators $\partial /\partial x^{i}$

${\mathbf {v} }={\frac {dx^{i}}{d\lambda }}{\frac {\partial \;\;}{\partial x^{i}}}={\frac {dx^{i}}{d\lambda }}{\mathbf {e} }_{i}$

where we have written ${\mathbf {e} }_{i}=\partial /\partial x^{i}$, the tangent vectors to the curves which are simply the coordinate grid itself.

If we adopt a new coordinates system ${x'}^{i},\;i=0,1,\dots$ then for each i, the old coordinate ${x^{i}}$ can be expressed as function of the new system, so $x^{i}({x'}^{j}),j=0,1,\dots$ Let ${\mathbf {e} }'_{i}={\partial }/{\partial {x'}^{i}}$ be the basis, tangent vectors in this new coordinates system. We can express ${\mathbf {e} }_{i}$ in the new system by applying the chain rule on x. As a function of coordinates we find the following transformation

${\mathbf {e} }'_{i}={\frac {\partial }{\partial {x'}^{i}}}={\frac {\partial x^{j}}{\partial {x'}^{i}}}{\frac {\partial }{\partial x^{j}}}={\frac {\partial x^{j}}{\partial {x'}^{i}}}{\mathbf {e} }_{j}$

which indeed is the same as the covariant transformation for the derivative of a function.

Contravariant transformation

The components of a (tangent) vector transform in a different way, called contravariant transformation. Consider a tangent vector v and call its components $v^{i}$ on a basis ${\mathbf {e} }_{i}$. On another basis ${\mathbf {e} }'_{i}$ we call the components ${v'}^{i}$, so

${\mathbf {v} }=\sum _{i}v^{i}{\mathbf {e} }_{i}=\sum _{i}{v'}^{i}{\mathbf {e} }'_{i}$

in which

$v^{i}={\frac {dx^{i}}{d\lambda }}\;{\mbox{ and }}\;{v'}^{i}={\frac {d{x'}^{i}}{d\lambda }}$

If we express the new components in terms of the old ones, then

${v'}^{i}={\frac {d{x'}^{i}}{d\lambda \;\;}}={\frac {\partial {x'}^{i}}{\partial x^{j}}}{\frac {dx^{j}}{d\lambda }}={\frac {\partial {x'}^{i}}{\partial x^{j}}}{v}^{j}$

This is the explicit form of a transformation called the contravariant transformation and we note that it is different and just the inverse of the covariant rule. In order to distinguish them from the covariant (tangent) vectors, the index is placed on top.

Differential forms transform contravariantly

An example of a contravariant transformation is given by a differential form df. For f as a function of coordinates $x^{i}$, df can be expressed in terms of $dx^{i}$. The differentials dx transform according to the contravariant rule since

$d{x'}^{i}=\sum _{j}{\frac {\partial {x'}^{i}}{\partial {x}^{j}}}{dx}^{j}$

Dual properties

Entities that transform covariantly (like basis vectors) and the ones that transform contravariantly (like components of a vector and differential forms) are "almost the same" and yet they are different. They have "dual" properties. What is behind this, is mathematically known as the dual space that always goes together with a given linear vector space.

Take any vector space T. A function f on T is called linear if, for any vectors v, w and scalar α:

$f({\mathbf {v} }+{\mathbf {w} })=f({\mathbf {v} })+f({\mathbf {w} })$

$f(\alpha {\mathbf {v} })=\alpha f({\mathbf {v} })$

A simple example is the function which assigns a vector the value of one of its components (called a projection function). It has a vector as argument and assigns a real number, the value of a component.

All such scalar-valued linear functions together form a vector space, called the dual space of T. One can easily see that, indeed, the sum f+g is again a linear function for linear f and g, and that the same holds for scalar multiplication αf.

Given a basis ${\mathbf {e} }_{i}$ for T, we can define a basis, called the dual basis for the dual space in a natural way by taking the set of linear functions mentioned above: the projection functions. So those functions ω that produce the number 1 when they are applied to one of the basis vector ${\mathbf {e} }_{i}$. For example ${\omega }^{0}$ gives a 1 on ${\mathbf {e} }_{0}$ and zero elsewhere. Applying this linear function ${\omega }^{0}$ to a vector ${\mathbf {v} }=v^{i}{\mathbf {e} }_{i}$, gives (using its linearity)

$\omega ^{0}({\mathbf {v} })=\omega ^{0}(v^{i}{\mathbf {e} }_{i})=v^{i}\omega ^{0}({\mathbf {e} }_{i})=v^{0}$

so just the value of the first coordinate. For this reason it is called the projection function.

There are as many dual basis vectors $\omega ^{i}$ as there are basis vectors ${\mathbf {e} }_{i}$, so the dual space has the same dimension as the linear space itself. It is "almost the same space", except that the elements of the dual space (called dual vectors) transform covariantly and the elements of the tangent vector space transform contravariantly.

Sometimes an extra notation is introduced where the real value of a linear function σ on a tangent vector u is given as

$\sigma [{\mathbf {u} }]:=\langle \sigma ,{\mathbf {u} }\rangle$

where $\langle \sigma ,{\mathbf {u} }\rangle$ is a real number. This notation emphasizes the bilinear character of the form. it is linear in σ since that is a linear function and it is linear in u since that is an element of a vector space.

Co- and contravariant tensor components

Without coordinates

With the aid of the section of dual space, a tensor of type (r,s) is simply defined as a real-valued multilinear function of r dual vectors and s vectors in a point p. So a tensor is defined in a point. It is a linear machine: feed it with vectors and dual vectors and it produces a real number. Since vectors (and dual vectors) are defined independent of coordinate system, this definition of a tensor is also free of coordinates and does not depend on the choice of a coordinate system. This is the main importance of tensors in physics.

The notation of a tensor is

$T(\sigma ,\ldots ,\rho ,{\mathbf {u} },\ldots ,{\mathbf {v} })\;{\mbox{ or as }}\;{T^{\sigma \ldots \rho }}_{{\mathbf {u} }\ldots {\mathbf {v} }}$

for dual vectors (differential forms) ρ, σ and tangent vectors ${\mathbf {u} },{\mathbf {v} }$. In the second notation the distinction between vectors and differential forms is more obvious.

With coordinates

Because a tensor depends linearly on its arguments, it is completely determined if one knows the values on a basis $\omega ^{i}\ldots \omega ^{j}$ and ${\mathbf {e} }_{k}\ldots {\mathbf {e} }_{l}$

$T(\omega ^{i},\ldots ,\omega ^{j},{\mathbf {e} }_{k}\ldots {\mathbf {e} }_{l})={T^{i\ldots j}}_{k\ldots l}$

The numbers ${T^{i\ldots j}}_{k\ldots l}$ are called the components of the tensor on the chosen basis.

If we choose another basis (which are a linear combination of the original basis), we can use the linear properties of the tensor and we will find that the tensor components in the upper indices transform as dual vectors (so contravariant), whereas the lower indices will transform as the basis of tangent vectors and are thus covariant. For a tensor of rank 2, we can easily verify that

${A'}_{ij}={\frac {\partial x^{l}}{\partial {x'}^{i}}}{\frac {\partial x^{m}}{\partial {x'}^{j}}}A_{lm}$ covariant tensor

${A'\,}^{ij}={\frac {\partial {x'}^{i}}{\partial x^{l}}}{\frac {\partial {x'}^{j}}{\partial x^{m}}}A^{lm}$ contravariant tensor

For a mixed co- and contravariant tensor of rank 2

${A'\,}^{i}{}_{j}={\frac {\partial {x'}^{i}}{\partial x^{l}}}{\frac {\partial x^{m}}{\partial {x'}^{j}}}A^{l}{}_{m}$ mixed co- and contravariant tensor