L10a140 link

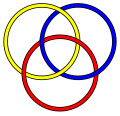
In the mathematical theory of knots, Marilyn's Cross is a three-component link of twelve crossings.

Marilyn's Cross was discovered independently by David Swart in 2010 and by Rick Mabry and Laura McCormick of Louisiana State University in Shreveport in 2011. In trying to identify the link, Swart, in collaboration with Dror Bar-Natan of the University of Toronto, declared that "It is what it is." This three component Brunnian link is today known as Marilyn's Cross, named for Mabry's late cousin, Marilyn Henry.

Description

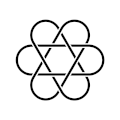
Marilyn's Cross is a three component, 12-crossing, non-alternating, Brunnian link.

The "cross" variation

The "cross" variation of Marilyn's Cross.

This is another configuration of Marilyn's Cross that is topologically equivalent to the "Star-of-David version" seen above. While the name, Marilyn's Cross refers to any equivalent configuration, some call this arrangement Marilyn's Cross and refer to the other as Marilyn's Star.

The benefit of the star configuration is that is allows for ease of comparison between Marilyn's Cross and similar links that were previously known, such as the Brunnian-Not-Borromean link.

Brunnian link

"Paper-clipped" components

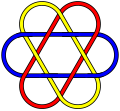
A Brunnian link is a link of connected components that, when one component is removed, becomes entirely unconnected. The best known example of a Brunnian link is the three-component Borromean rings. A 12-crossing, three component example of a Brunnian link that, at first glance, looks very much like Marilyn's Cross is the alternating "Brunnian-Not-Borromean" link.

• 
  The Borromean Rings
• 
  "Brunnian-Not-Borromean"

Marilyn's Cross is a Brunnian link that differs from most other examples in two ways. First, it is not an alternating link. That is to say, the crossings do not alternate in a strictly over-under fashion. Second, each component of most Brunnian links lies entirely on top of or beneath any other component. However, the components of Marilyn's Cross are pairwise "paper-clipped". Any pair of components has a crossing configuration of over-over-under-under.

Invariants

The Alexander polynomial for Marilyn's Cross is

$\Delta (t)=t^{4}-4t^{3}+8t^{2}-12t-12t^{-1}+8t^{-2}-4t^{-3}+t^{-4}+14,\,$

the multivariable Alexander polynomial is

$\Delta (u,v,w)={\frac {(u-1)(v-1)(w-1)(vw+1)^{2}}{vw{\sqrt {uvw}}}},\,$

the Conway polynomial is

$\nabla (z)=4z^{4}+4z^{6}+z^{8},\,$

the Jones polynomial factors nicely as

${\begin{aligned}V(t)&=-t^{5}+3t^{4}-5t^{3}+8t^{2}-9t+12-9t^{-1}+8t^{-2}-5t^{-3}+3t^{-4}-t^{-5}\\&=-{\frac {1}{t^{5}}}\left(t^{5}-2t^{4}+t^{3}-2t^{2}+t-1\right)\left(t^{5}-t^{4}+2t^{3}-t^{2}+2t-1\right)\\&=w(t)w(1/t),\,\end{aligned}}$

where $w(t)=t^{5}-2t^{4}+t^{3}-2t^{2}+t-1.$ (Notice that $w(t)$ is essentially the Jones polynomial for the Whitehead link.)

The HOMFLY polynomial is

$P(\alpha ,z)=z^{-2}\alpha ^{-2}-4z^{2}\alpha ^{-2}-4z^{4}\alpha ^{-2}-z^{6}\alpha ^{-2}-2z^{-2}+8z^{2}+12z^{4}+6z^{6}+z^{8}+z^{-2}\alpha ^{2}-4z^{2}\alpha ^{2}-4z^{4}\alpha ^{2}-z^{6}\alpha ^{2},\,$

and the Kauffman polynomial is

${\begin{aligned}F(a,z)&=1+2z^{-2}+a^{-2}z^{-2}+a^{2}z^{-2}-2a^{-1}z^{-1}-az^{-1}-20z^{2}+2a^{-4}z^{2}\\&{}-8a^{-2}z^{2}-8a^{2}z^{2}+2a^{4}z^{4}+2a^{4}z^{2}-2a^{-5}z^{3}+4a^{-3}z^{3}+6a^{-1}z^{3}\\&{}+6az^{3}+4a^{3}z^{3}-2a^{5}z^{3}+42z^{4}-7a^{-4}z^{4}+14a^{-2}z^{4}\\&{}+14a^{2}z^{4}-7a^{4}z^{4}+a^{-5}z^{5}-9a^{-3}z^{5}-2a^{-1}z^{5}-2az^{5}-9a^{3}z^{5}\\&{}+a^{5}z^{5}-28z^{6}+3a^{-4}z^{6}-11a^{-2}z^{6}-11a^{2}z^{6}+3a^{4}z^{6}+4a^{-3}z^{7}\\&{}-2a^{-1}z^{7}-2az^{7}+4a^{3}z^{7}+8z^{8}+4a^{-2}z^{8}+4a^{2}z^{8}+2a^{-1}z^{9}+2az^{9}.\end{aligned}}$

Symmetry

The bilateral symmetry of Marilyn's Cross.

Marilyn's Cross displays bilateral symmetry, as is illustrated in the symmetric nature of its invariant polynomials.

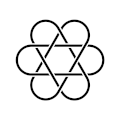
Marilyn's Cross is chiral, i.e., it is topologically distinguishable from its mirror image.

• 
  Marilyn's Cross.
• 
  Mirror image of Marilyn's Cross---"It is what it is".

External links

• Multivariable Alexander Polynomial
• The Knot Atlas
• "It Is What It Is"