Rope (data structure)

In computer programming a rope, or cord, is a data structure for efficiently storing and manipulating a very long string. For example, a text editing program may use a rope to represent the text being edited, so that operations such as insertion, deletion, and random access can be done efficiently.^[1]

Description

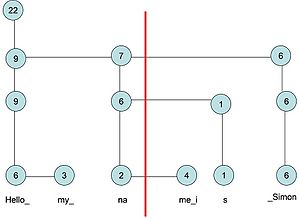
A rope is a binary tree. Leaf nodes (as well as some single-child internal nodes) contain a short string. Each node has a "weight" equal to the length of its string plus the sum of all the weights in its left subtree. Thus a node with two children divides the whole string into two parts: the left subtree stores the first part of the string. The right subtree stores the second part and its weight is the sum of the left childs weight and the length of its contained string.

The binary tree can be seen as several levels of nodes. The bottom level contains all the nodes that contain a string. Higher levels have fewer and fewer nodes. The top level consists of a single "root" node. The rope is built by putting the nodes with short strings in the bottom level, then attaching a random half of the nodes to parent nodes in the next level. Nodes with no parent (for example, the two nodes storing the strings "my_" and "me_i" in the diagram above) become the right child of the node located immediately to their left, thus forming a chain.

Operations

Index

Definition: Index(i): return the character at position i

Time complexity: O(log N) where N is the length of the rope

To retrieve the i-th character, we begin a recursive search from the root node:

// Note: Assumes 1-based indexing.
function index(RopeNode node, integer i)
    if node.weight < i then
        return index(node.right, i - node.weight)
    else
        if exists(node.left) then
            return index(node.left, i)
        else
            return node.string[i]
        endif
    endif
end

For example,to find the character at i=10 in the following rope, start at the root node, find that 22 is greater than 10 and there is a left child, so go to the left child. 9 is less than 10, so subtract 9 from 10 (leaving i=1) and go to the right child. Then because 7 is greater than 1 and there's a left child, go to the left child. 6 is greater than 1 and there's a left child, so go to the left child again. Finally 2 is greater than 1 but there is no left child, so the character at index 1 of the short string "na", is the answer.

Split

Definition: Split (i, S): split the string S into two new strings S1 and S2, S1 = C1, …, Ci and S2 = Ci + 1, …, Cm.

Time complexity: O(log N)

There are two cases: in the first, the i-th character is at the end of an array such as in the following picture; in the second, the character is in the middle of an array. The second case reduces to the first case as follows: split the node at the character into two nodes each with part of the array and make the second node the right child of the first node.

For example, to split the pictured rope into two parts, query the i-th character to locate the node v at the bottom level. Remove the link between v and the right child of v, or v’. Go to the parent u and subtract the weight of v’ from the weight of u. Since the parent has the right child of u, now u’, modify u’ to link to v’ and increase the weight of u’ by the weight of v’. The former left child of u’ becomes the right child of v’, creating the second picture. Continue up to the parent of u, w. Subtract the weight of v’ from the weight of w. Then modify the right child of w, now w’, to link to u’. The former child of w’ becomes the right child of u’. Increase the weight of w’ by the weight of v’. Move to the parent of w, x. Since w is already the right child of x, there is no change. Then go to the parent of x, y, and reduce the weight of y by the weight of w’.

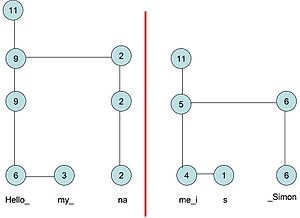
Concat

Definition: Concat(S1, S2): concatenate two ropes S1, S2 into a single rope.

Time complexity: O(log N)

This operation is the reverse of split. Alternatively, create a new root node with left=S1 and right=S2. This is constant time, but can lead to an unbalanced tree.

Insert

Definition: Insert(i, S’): insert the string S’ beginning at position i in the string s, to form a new string C1, …, Ci, S’, Ci + 1, …, Cm.

Time complexity: O(log N).

This operation can be done by a split() and a concat(). The cost is the sum of the two.

Delete

Definition: Delete(i, j): delete the substring Ci, …, Ci + j − 1, from s to form a new string C1, …, Ci − 1, Ci + j, …, Cm.

Time complexity: O(log N).

This operation can be done by two split() and a concat(). First, split the rope in three, divided by i-th and j-th character respectively, putting the string to delete in a separate node. Then concatenate the other two nodes.

Report

Definition: Report(i, j): output the string Ci, …, Ci + j − 1.

Time complexity: O(j + log N)

To report the string Ci, …, Ci + j − 1, find the node u that contains ci and weight(u) >= j, and then traverse T starting at node u. Output Ci, …, Ci + j − 1 by doing an in-order traversal of T starting at node u.

Comparison with monolithic arrays

Advantages:

Ropes enable much faster insertion and deletion of text than monolithic string arrays, on which operations have time complexity O(n).
Ropes don't require the extra O(n) memory that arrays need for copying operations, and ropes don't require large contiguous memory spaces.

Disadvantages:

Slightly greater overall space usage (mainly to store parent nodes)
Increase in time to manage the extra storage

This table compares the algorithmic characteristics of string and rope implementations, not their "raw speed". Array-based strings have smaller overhead, so (for example) concatenation and split operations are faster on small datasets. However, when array-based strings are used for longer strings, time complexity and memory usage for insertion and deletion of characters become unacceptably large. A rope data structure, on the other hand, has stable performance regardless of data size. Moreover, the space complexity for ropes and arrays are both O(n). In summary, ropes are better suited when the data is large and frequently modified.

Performance
Operation	Rope	String
Index^[1]	O(log n)	O(1)
Split^[1]	O(log n)	O(1)
Concatenate	O(log n)	O(n)
Iterate over each character^[1]	O(n)	O(n)
Insert	O(log n)	O(n)
Delete	O(log n)	O(n)
Report	O(j + log n)	O(j)
Build	O(n)	O(n)

^{[citation needed]}

References

^ ^a ^b ^c ^d ^e Boehm, Hans-J (December 1995). "Ropes: an Alternative to Strings" (PDF). Software—Practice & Experience. 25 (12). New York, NY, USA: John Wiley & Sons, Inc.: 1315–1330. doi:10.1002/spe.4380251203. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)

External links

[Boehm-1] Boehm, Hans-J (December 1995). "Ropes: an Alternative to Strings" (PDF). Software—Practice & Experience. 25 (12). New York, NY, USA: John Wiley & Sons, Inc.: 1315–1330. doi:10.1002/spe.4380251203. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)

[1]