Bialgebra
This article needs additional citations for verification. (December 2009) |
In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a coalgebra, such that these structures are compatible.
Compatibility means that the comultiplication and the counit are both unital algebra homomorphisms, or equivalently, that the multiplication and the unit of the algebra both be coalgebra morphisms: these statements are equivalent in that they are expressed by the same diagrams. A bialgebra homomorphism is a linear map that is both an algebra and a coalgebra homomorphism.
As reflected in the symmetry of the diagrams, the definition of bialgebra is self-dual, so if one can define a dual of B (which is always possible if B is finite-dimensional), then it is automatically a bialgebra.
| Algebraic structures |
|---|
Formal definition
(B, ∇, η, Δ, ε) is a bialgebra over K if it has the following properties:
- B is a vector space over K;
- there are K-linear maps (multiplication) ∇: B ⊗ B → B (equivalent to K-multilinear map ∇: B ⊗ B → B) and (unit) η: K → B, such that (B, ∇, η) is a unital associative algebra;
- there are K-linear maps (comultiplication) Δ: B → B ⊗ B and (counit) ε: B → K, such that (B, Δ, ε) is a (counital coassociative) coalgebra;
- compatibility conditions expressed by the following commutative diagrams:
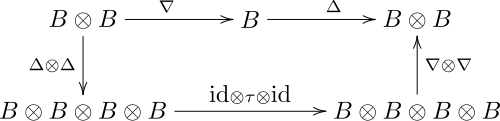
- Multiplication ∇ and comultiplication Δ [1]
where τ: B ⊗ B → B ⊗ B is the linear map defined by τ(x ⊗ y) = y ⊗ x for all x and y in B,
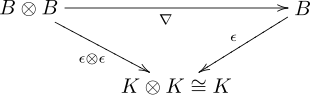
- Multiplication ∇ and counit ε
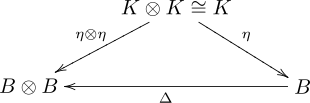
- Comultiplication Δ and unit η [2]
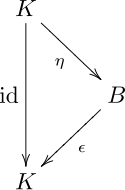
- Unit η and counit ε
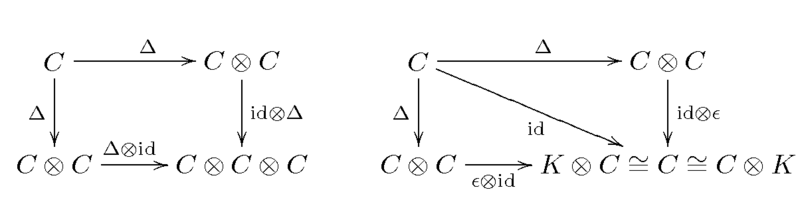
Coassociativity and counit
The K-linear maps Δ: B → B ⊗ B is coassociative if
The K-linear map ε: B → K is a counit if .
Coassociativy and counit are expressed by the commutativity of the following two diagrams with B in place of C (they are the duals of the diagrams expressing associativity and unit of an algebra):
Compatibility conditions
The four commutative diagrams can be read either as "comultiplication and counit are homomorphisms of algebras" or, equivalently, "multiplication and unit are homomorphisms of coalgebras".
These statements are meaningful once we explain the natural structures of algebra and coalgebra in all the vector spaces involved besides B: (K, ∇0, η0) is a unital associative algebra in an obvious way and (B ⊗ B, ∇2, η2) is a unital associative algebra with unit and multiplication
- ,
so that or, omitting ∇ and writing multiplication as juxtaposition, ;
similarly, (K, Δ0, ε0) is a coalgebra in an obvious way and B ⊗ B is a coalgebra with counit and comultiplication
- .
Then, diagrams 1 and 3 say that Δ: B → B ⊗ B is a homomorphism of unital (associative) algebras (B, ∇, η) and (B ⊗ B, ∇2, η2)
- , or simply Δ(xy) = Δ(x) Δ(y),
- , or simply Δ(1B) = 1B ⊗ B;
diagrams 2 and 4 say that ε: B → K is a homomorphism of unital (associative) algebras (B, ∇, η) and (K, ∇0, η0):
- , or simply ε(xy) = ε(x) ε(y)
- , or simply ε(1B) = 1K.
Equivalently, diagrams 1 and 2 say that ∇: B ⊗ B → B is a homomorphism of (counital coassociative) coalgebras (B ⊗ B, Δ2, ε2) and (B, Δ, ε):
- ;
diagrams 3 and 4 say that η: K → B is a homomorphism of (counital coassociative) coalgebras (K, Δ0, ε0) and (B, Δ, ε):
- .
Examples
Examples of bialgebras include the Hopf algebras[3]. Similar structures with different compatibility between the product and coproduct, or different types of product and coproduct, include Lie bialgebras and Frobenius algebras. Additional examples are given in the article on coalgebras.
See also
Notes
- ^ Dăscălescu, Năstăsescu & Raianu (2001), Template:Google books quote
- ^ Dăscălescu, Năstăsescu & Raianu (2001), Template:Google books quote
- ^ Dăscălescu, Năstăsescu & Raianu (2001), Template:Google books quote
References
- Dăscălescu, Sorin; Năstăsescu, Constantin; Raianu, Șerban (2001), Hopf Algebras, Pure and Applied Mathematics, vol. 235 (1st ed.), Marcel Dekker, ISBN 0-8247-0481-9
{{citation}}: Unknown parameter|subtitle=ignored (help).