Cubic crystal system

A cubic crystal system is a crystal where the unit cell, the unit which repeats to form the crystal, is in the shape of a cube. This is one of the most common shapes found in metallic crystals, and being the simplest, is the first to be taught to students.

The three Bravais lattices that form the cubic crystal system are:

simple cubic (sc)	body-centered cubic (bcc)	face-centered cubic (fcc)
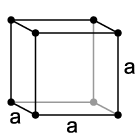
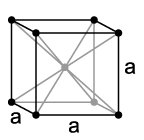
		Cubic, face-centered

The simple cubic system consists of one atom on each corner. Please note that the atoms on the edges, faces, or corners of the unit cell are only partly in the cell. Thus, the simple cubic unit cell contains only one atom (1/8th * 8). Also, though in the picture, atoms are shown as dots, the atoms are really touching, filling the majority of the volume of the atom. The atomic packing factor, the fraction of space occupied by the atoms, is only .524. Due to its low density, it is a high energy structure and is rare in nature.

The body centered cubic, abbreviated BCC, contains one atom in the center and the eight corner atoms. Thus, it has (1/8th *8 + 1) 2 atoms in the cell. However, due to its design, has a density of .680. Its low energy structure makes it fairly common in nature.

Face centered cubic (FCC), contains one atom in each corner and one on each face. Thus, it has (1/8 * 8 + 1/2*6) 4 atoms in it's cell. It has a density of .741, a ratio that it shares with several other systems, including hexagonal close packed and one version of tetrahedral BCC. This number, .741, is the most tightly packed crystal possible with spherical atoms,

Several ionicaly bonded atoms also form a cubic structure.

When the two atoms are of the same size, they have what is called the "interpenetrating simple cubic", where two atoms of a different type have individual simple cubic crystals. However, the unit cell consists of the atom of one being in the middle of the four corners, structurally resembling body centered cubic. The most common example is CsCl.

This article is under construction. The old article, which was deemed confusing, is below. _______________________________________________

The cubes drawn are the conventional unit cells. For a cube whose vertices include 000 and 200, bcc has additional lattice point 111, while fcc has 110, 101, and 011. For bcc the primitive cells have a volume of 1/2 of the cube, e.g. the parallelepiped 000 200 020 220 111 311 131 331 with primitive translation vectors 200, 020, and 111, with determinant 4. For fcc the primitive cells have a volume of 1/4 of the cube, e.g. the parallelepiped 110 220 020 130 101 211 011 121 with primitive translation vectors 110, -1 1 0, and 0 -1 1, with determinant 2.

As can be seen by turning the base plane 45°, bcc and fcc only differ by a vertical scaling: in both cases the lattice points in the middle layer are above the centers of the squares of the base layer. Both scales are "special", allowing a cubic symmetry: for bcc the middle layer has a height of 1/2 of the grid size of the square grid of each layer, while for fcc the middle layer has a height of 1/2 √2 of that grid size. For other scalings both are the same, body-centered tetragonal.

Perpendicular to each body diagonal, fcc has hexagonal layers, with three positionings, which are cyclically changed. Two opposite vertices of the cube have two layers in between. See also: close-packing

The point groups that fall under this crystal system are listed below, followed by their representations in international notation and Schoenflies notation, and mineral examples.

name	international		Schoenflies	example
hexoctahedral	${\frac {4}{m}}{\overline {3}}{\frac {2}{m}}$	or $m3m$	O_h	galena
gyroidal	432		O	petzite
diploidal	${\frac {2}{m}}{\overline {3}}$	or $m3$	T_h	pyrite
tetrahedral	${\overline {4}}3m$		T_d	sphalerite
tetartohedral	23		T

There are 36 cubic space groups, of which 10 are hexoctahedral: Fd3c, Fd3m, Fm3c, Fm3m, Ia3d, Im3m, Pm3m, Pm3n, Pn3m, and Pn3n. Other terms for hexoctahedral are normal class, holohedral, ditesseral central class, galena type.

Halite structure

Sodium chloride forms fcc crystals. In these, the larger chloride ions are arranged in a cubic close-packing, while the smaller sodium ions fill the octahedral gaps between them. Each ion is surrounded by six of the other kind. This same basic structure is found in many other minerals, and is known as the halite structure.

The sodium ions indicated in blue show that the fcc lattice can also be represented by mid-edge and centered lattice points, without lattice points at the vertices of the cube.

References

Hurlbut, Cornelius S.; Klein, Cornelis, 1985, Manual of Mineralogy, 20th ed., Wiley, ISBN 0471805807