Pi

Lower-case π (the lower case letter is usually used for the constant)

The mathematical constant π is an irrational number, approximately equal to 3.14159, which is the ratio of a circle's circumference to its diameter in Euclidean geometry, and has many uses in mathematics, physics, and engineering. It is also known as Archimedes' constant (not to be confused with Archimedes number) and Ludolph's number.

The letter π

The name of the Greek letter π is pi, and this spelling is used in typographical contexts where the Greek letter is not available or where its usage could be problematic. When referring to this constant, the symbol π is always pronounced like "pie" in English, the conventional English pronunciation of the letter.

The constant is named π because it is the first letter of the Greek words "περιφέρεια" (periphery) and "περίμετρον" (perimeter).

Definition

Area of the circle = π × area of the shaded square

In Euclidean plane geometry, π is defined either as the ratio of a circle's circumference to its diameter, or as the ratio of a circle's area to the area of a square whose side is the radius. π may be defined in many other ways, for example as the smallest positive x for which sin(x) = 0. See other formulas below. All these definitions are equivalent.

Numerical value

The numerical value of π, truncated to 50 decimal places is:

3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510...

See the the links below and those at sequence A00796 in OEIS for more digits.

Although this precision is more than sufficient for use in engineering and science, the exact value of π has an infinite decimal expansion: its decimal expansion never ends and does not repeat, since π is an irrational number (and indeed, a transcendental number). Much effort over the last few centuries has been put into computing more digits and investigating the number's properties. Despite much analytical work, and supercomputer calculations that have determined over 1 trillion digits of π, no pattern in the digits has ever been found. Digits of π are available on many web pages, and there is software for calculating π to billions of digits on any personal computer. See history of numerical approximations of π.

Properties

π is an irrational number; that is, it cannot be written as the ratio of two integers, as was proven in 1761 by Johann Heinrich Lambert.

π is also transcendental, as was proven by Ferdinand von Lindemann in 1882. This means that there is no polynomial with rational coefficients of which π is a root. An important consequence of the transcendence of π is the fact that it is not constructible. Because the coordinates of all points that can be constructed with compass and straightedge are constructible numbers, it is impossible to square the circle: that is, it is impossible to construct, using compass and straightedge alone, a square whose area is equal to the area of a given circle.

Formulae

Geometry

π appears in many formulæ in geometry involving circles and spheres.

Geometrical shape	Formula
Circumference of circle of radius r and diameter d	$C=2\pi r=\pi d\,\!$
Area of circle of radius r	$A=\pi r^{2}={\frac {1}{4}}\pi d^{2}\,\!$
Area of ellipse with semiaxes a and b	$A=\pi ab\,\!$
Volume of sphere of radius r and diameter d	$V={\frac {4}{3}}\pi r^{3}={\frac {1}{6}}\pi d^{3}\,\!$
Surface area of sphere of radius r and diameter d	$A=4\pi r^{2}=\pi d^{2}\,\!$
Volume of cylinder of height h and radius r	$V=\pi r^{2}h\,\!$
Surface area of cylinder of height h and radius r	$A=2(\pi r^{2})+(2\pi r)h=2\pi r(r+h)\,\!$
Volume of cone of height h and radius r	$V={\frac {1}{3}}\pi r^{2}h\,\!$
Surface area of cone of height h and radius r	$A=\pi r{\sqrt {r^{2}+h^{2}}}+\pi r^{2}=\pi r(r+{\sqrt {r^{2}+h^{2}}})\,\!$

(All of these are a consequence of the first one, as the area of a circle can be written as A = ∫(2πr) dr ("sum of annuli of infinitesimal width"), and others concern a surface or solid of revolution.)

Also, the angle measure of 180° (degrees) is equal to π radians.

Analysis

Many formulæ in analysis contain π, including infinite series (and infinite product) representations, integrals, and so-called special functions.

• Half the area of the unit disc:

$\int _{-1}^{1}{\sqrt {1-x^{2}}}\,dx={\frac {\pi }{2}}$

• Half the circumference of the unit circle:

$\int _{-1}^{1}{\frac {dx}{\sqrt {1-x^{2}}}}=\pi$

• François Viète, 1593 (proof):

${\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2}}}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\cdot \cdots ={\frac {2}{\pi }}$

• Leibniz' formula (proof):

$\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}={\frac {1}{1}}-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-\cdots ={\frac {\pi }{4}}$

• Wallis product (proof):

$\prod _{n=1}^{\infty }\left({\frac {n+1}{n}}\right)^{(-1)^{n-1}}={\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\cdots ={\frac {\pi }{2}}$

• Faster product (see Sondow, 2005 and Sondow web page)

$\left({\frac {2}{1}}\right)^{1/2}\left({\frac {2^{2}}{1\cdot 3}}\right)^{1/4}\left({\frac {2^{3}\cdot 4}{1\cdot 3^{3}}}\right)^{1/8}\left({\frac {2^{4}\cdot 4^{4}}{1\cdot 3^{6}\cdot 5}}\right)^{1/16}\cdots ={\frac {\pi }{2}}$

• Symmetric formula (see Sondow, 1997)

${\frac {\prod _{n=1}^{\infty }\left(1+{\frac {1}{4n^{2}-1}}\right)}{\sum _{n=1}^{\infty }{\frac {1}{4n^{2}-1}}}}={\frac {\left(1+{\frac {1}{3}}\right)\left(1+{\frac {1}{15}}\right)\left(1+{\frac {1}{35}}\right)\cdots }{{\frac {1}{3}}+{\frac {1}{15}}+{\frac {1}{35}}+\cdots }}=\pi$

• Bailey-Borwein-Plouffe algorithm (See Bailey, 1997 and Bailey web page)

$\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {4}{8k+1}}-{\frac {2}{8k+4}}-{\frac {1}{8k+5}}-{\frac {1}{8k+6}}\right)=\pi$

• An integral formula from calculus (see also Error function and Normal distribution):

$\int _{-\infty }^{\infty }e^{-x^{2}}\,dx={\sqrt {\pi }}$

• Basel problem, first solved by Euler (see also Riemann zeta function):

$\zeta (2)={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots ={\frac {\pi ^{2}}{6}}$

$\zeta (4)={\frac {1}{1^{4}}}+{\frac {1}{2^{4}}}+{\frac {1}{3^{4}}}+{\frac {1}{4^{4}}}+\cdots ={\frac {\pi ^{4}}{90}}$

and generally, $\zeta (2n)$ is a rational multiple of $\pi ^{2n}$ for positive integer n

• Gamma function evaluated at 1/2:

$\Gamma \left({1 \over 2}\right)={\sqrt {\pi }}$

• Stirling's approximation:

$n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}$

• Euler's identity (called by Richard Feynman "the most remarkable formula in mathematics"):

$e^{i\pi }+1=0\;$

• A property of Euler's totient function (see also Farey sequence):

$\sum _{k=1}^{n}\phi (k)\sim {\frac {3n^{2}}{\pi ^{2}}}$

• An application of the residue theorem

$\oint {\frac {dz}{z}}=2\pi i,$

where the path of integration is a closed curve around the origin, traversed in the standard counterclockwise direction.

Continued fractions

Next to its simple continued-fraction representation [3; 7, 15, 1, 292, 1, 1, …], which displays no discernible pattern, π has many generalized continued-fraction representations that are generated by a simple rule, including:

${\frac {4}{\pi }}=1+{\cfrac {.1}{3+{\cfrac {.4}{5+{\cfrac {9}{.7+{\cfrac {.16}{9+{\cfrac {.25}{11+{\cfrac {.36}{13+\cdots }}}}}}}}}}}}$

(Other representations are available at The Wolfram Functions Site.)

Number theory

Some results from number theory:

• The probability that two randomly chosen integers are coprime is 6/π².

• The probability that a randomly chosen integer is square-free is 6/π².

• The average number of ways to write a positive integer as the sum of two perfect squares (order matters) is π/4.

• The product of (1 − 1/p²) over the primes, p, is 6/π².$\prod _{p\in \mathbb {P} }\left(1-{\frac {1}{p^{2}}}\right)={\frac {6}{\pi ^{2}}}$

Here, "probability", "average", and "random" are taken in a limiting sense, e.g. we consider the probability for the set of integers {1, 2, 3,…, N}, and then take the limit as N approaches infinity.

The theory of elliptic curves and complex multiplication derives the approximation

$\pi \approx {\ln(640320^{3}+744) \over {\sqrt {163}}}$

which is valid to about 30 digits.

Dynamical systems and ergodic theory

Consider the recurrence relation

$x_{i+1}=4x_{i}(1-x_{i})\,$

Then for almost every initial value x₀ in the unit interval [0,1],

$\lim _{n\to \infty }{\frac {1}{n}}\sum _{i=1}^{n}{\sqrt {x_{i}}}={\frac {2}{\pi }}$

This recurrence relation is the logistic map with parameter r = 4, known from dynamical systems theory. See also: ergodic theory.

Physics

The number π appears routinely in equations describing fundamental principles of the universe, due in no small part to its relationship to the nature of the circle and, correspondingly, spherical coordinate systems.

• The cosmological constant:

$\Lambda ={{8\pi G} \over {3c^{2}}}\rho$

• Heisenberg's uncertainty principle:

$\Delta x\Delta p\geq {\frac {h}{4\pi }}$

• Einstein's field equation of general relativity:

$R_{ik}-{g_{ik}R \over 2}+\Lambda g_{ik}={8\pi G \over c^{4}}T_{ik}$

• Coulomb's law for the electric force:

$F={\frac {\left|q_{1}q_{2}\right|}{4\pi \epsilon _{0}r^{2}}}$

• Magnetic permeability of free space:

$\mu _{0}=4\pi \cdot 10^{-7}\,\mathrm {N/A^{2}} \,$

Probability and statistics

In probability and statistics, there are many distributions whose formulæ contain π, including:

• probability density function (pdf) for the normal distribution with mean μ and standard deviation σ:

$f(x)={1 \over \sigma {\sqrt {2\pi }}}\,e^{-(x-\mu )^{2}/(2\sigma ^{2})}$

• pdf for the (standard) Cauchy distribution:

$f(x)={\frac {1}{\pi (1+x^{2})}}$

Note that since $\int _{-\infty }^{\infty }f(x)\,dx=1$, for any pdf f(x), the above formulæ can be used to produce other integral formulae for π.

A semi-interesting empirical approximation of π is based on Buffon's needle problem. Consider dropping a needle of length L repeatedly on a surface containing parallel lines drawn S units apart (with S > L). If the needle is dropped n times and x of those times it comes to rest crossing a line (x > 0), then one may approximate π using:

$\pi \approx {\frac {2nL}{xS}}$

[As a practical matter, this approximation is poor and converges very slowly.]

Another approximation of π is to throw points randomly into a quarter of a circle with radius 1 that is inscribed in a square of length 1. π, the area of a unit circle, is then approximated as 4*(points in the quarter circle) / (total points).

History

Main article: History of π

Use of the symbol π

Often William Jones' book A New Introduction to Mathematics from 1706 is cited as the first text where the Greek letter π was used for this constant, but this notation became popular especially since Leonhard Euler adopted it some years later, (cf. History of π).

Early approximations

Main article: History of numerical approximations of π.

The value of π has been known in some form since antiquity. As early as the 19th century BC, Babylonian mathematicians were using π=25/8, which is within 0.5% of the true value.

The Egyptian scribe Ahmes wrote the oldest known text to give an approximate value for π, citing a Middle Kingdom papyrus, corresponding to a value of 256 divided by 81 or 3.160.

It is sometimes claimed that the Bible states that π=3, based on a passage in 1 Kings 7:23 giving measurements for a round basin as having a 10 cubit diameter and a 30 cubit circumference. Rabbi Nehemiah explained this by the diameter being from outside to outside while the circumference was the inner brim; but it may suffice that the measurements are given in round numbers. Also, the basin may not have been exactly circular.

Principle of Archimedes' method to approximate π.

Archimedes of Syracuse discovered, by considering the perimeters of 96-sided polygons inscribing a circle and inscribed by it, that π is between 223/71 and 22/7. The average of these two values is roughly 3.1419.

The Chinese mathematician Liu Hui computed π to 3.141014 (good to three decimal places) in AD 263 and suggested that 3.14 was a good approximation.

The Indian mathematician and astronomer Aryabhata in the 5th century gave the approximation π = 62832/20000 = 3.1416, correct when rounded off to four decimal places.

The Chinese mathematician and astronomer Zu Chongzhi computed π to be between 3.1415926 and 3.1415927 and gave two approximations of π, 355/113 and 22/7, in the 5th century.

The Indian mathematician and astronomer Madhava of Sangamagrama in the 14th century computed the value of π after transforming the power series expansion of π/4 into the form

π = √12 (1 - 1/(33) + 1/(532) - 1/(733) + ...

and using the first 21 terms of this series to compute a rational approximation of π correct to 11 decimal places as 3.14159265359. By adding a remainder term to the original power series of π/4, he was able to compute π to an accuracy of 13 decimal places.

The astronomer Ghyath ad-din Jamshid Kashani (1350-1439) correctly computed π to 9 digits in the base of 60, which is equivalent to 16 decimal digits as:

2π = 6.2831853071795865

The German mathematician Ludolph van Ceulen in 1615 computed the first 32 decimal places of π. He was so proud of this accomplishment that he had them inscribed on his tombstone.

In 1789, the Slovene mathematician Jurij Vega improved John Machin's formula from 1706 and calculated the first 140 decimal places for π of which the first 126 were correct [1] and held the world record for 52 years until 1841, when William Rutherford calculated 208 decimal places of which the first 152 were correct.

The English amateur mathematician William Shanks, a man of independent means, spent over 20 years calculating π to 707 decimal places (accomplished in 1873). In 1944, D. F. Ferguson found (with the aid of a mechanical desk calculator) that Shanks had made a mistake in the 528th decimal place, and that all succeeding digits were fallacious.

Numerical approximations

Main article: History of numerical approximations of π

Due to the transcendental nature of π, there are no closed form expressions for the number in terms of algebraic numbers and functions. Therefore numerical calculations must use approximations of π. For many purposes, 3.14 or 22/7 is close enough, although engineers often use 3.1416 (5 significant figures) or 3.14159 (6 significant figures) for more accuracy. The approximations 22/7 and 355/113, with 3 and 7 significant figures respectively, are obtained from the simple continued fraction expansion of π. The approximation 355/113 (3.1415929…) is the best one that may be expressed with a three-digit numerator and denominator.

The earliest numerical approximation of π is almost certainly the value 3. In cases where little precision is required, it may be an acceptable substitute. That 3 is an underestimate follows from the fact that it is the ratio of the perimeter of an inscribed regular hexagon to the diameter of the circle.

All further improvements to the above mentioned "historical" approximations were done with the help of computers.

Efficient methods

In the early years of the computer, the first expansion of π to 100,000 decimal places was computed by Maryland mathematician Dr. Daniel Shanks and his team at the United States Naval Research Laboratory (N.R.L.) in 1961. Dr. Shanks's son Oliver Shanks, also a mathematician, states that there is no family connection to William Shanks, and in fact, his family's roots are in Central Europe.

Daniel Shanks and his team used two different power series for calculating the digital of π. For one it was known that any error would produce a value slightly high, and for the other, it was known that any error would produce a value slightly low. And hence, as long as the two series produced the same digits, there was a very high confidence that they were correct. The first 100,000 digits of π were published by the US Naval Research Laboratory

None of the formulæ given above can serve as an efficient way of approximating π. For fast calculations, one may use a formula such as Machin's:

${\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}$

together with the Taylor series expansion of the function arctan(x). This formula is most easily verified using polar coordinates of complex numbers, starting with

$(5+i)^{4}\cdot (-239+i)=-114244-114244i.$

Formulæ of this kind are known as Machin-like formulae.

Many other expressions for π were developed and published by the incredibly-intuitive Indian mathematician Srinivasa Ramanujan. He worked with mathematician Godfrey Harold Hardy in England for a number of years.

Extremely long decimal expansions of π are typically computed with the Gauss-Legendre algorithm and Borwein's algorithm; the Salamin-Brent algorithm which was invented in 1976 has also been used.

The first one million digits of π and 1/π are available from Project Gutenberg (see external links below). The current record (December 2002) by Yasumasa Kanada of Tokyo University stands at 1,241,100,000,000 digits, which were computed in September 2002 on a 64-node Hitachi supercomputer with 1 terabyte of main memory, which carries out 2 trillion operations per second, nearly twice as many as the computer used for the previous record (206 billion digits). The following Machin-like formulæ were used for this:

${\frac {\pi }{4}}=12\arctan {\frac {1}{49}}+32\arctan {\frac {1}{57}}-5\arctan {\frac {1}{239}}+12\arctan {\frac {1}{110443}}$

K. Takano (1982).

${\frac {\pi }{4}}=44\arctan {\frac {1}{57}}+7\arctan {\frac {1}{239}}-12\arctan {\frac {1}{682}}+24\arctan {\frac {1}{12943}}$

F. C. W. Störmer (1896).

These approximations have so many digits that they are no longer of any practical use, except for testing new supercomputers. (Normality of π will always depend on the infinite string of digits on the end, not on any finite computation.)

In 1997, David H. Bailey, Peter Borwein and Simon Plouffe published a paper (Bailey, 1997) on a new formula for π as an infinite series:

$\pi =\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {4}{8k+1}}-{\frac {2}{8k+4}}-{\frac {1}{8k+5}}-{\frac {1}{8k+6}}\right)$

This formula permits one to fairly readily compute the k^th binary or hexadecimal digit of π, without having to compute the preceding k − 1 digits. Bailey's website contains the derivation as well as implementations in various programming languages. The PiHex project computed 64-bits around the quadrillionth bit of π (which turns out to be 0).

Fabrice Bellard claims to have beaten the efficiency record set by Bailey, Borwein, and Plouffe with his formula to calculate binary digits of π [2]:

$\pi ={\frac {1}{2^{6}}}\sum _{n=0}^{\infty }{\frac {{(-1)}^{n}}{2^{10n}}}\left(-{\frac {2^{5}}{4n+1}}-{\frac {1}{4n+3}}+{\frac {2^{8}}{10n+1}}-{\frac {2^{6}}{10n+3}}-{\frac {2^{2}}{10n+5}}-{\frac {2^{2}}{10n+7}}+{\frac {1}{10n+9}}\right)$

Other formulæ that have been used to compute estimates of π include:

${\frac {\pi }{2}}=\sum _{k=0}^{\infty }{\frac {k!}{(2k+1)!!}}=1+{\frac {1}{3}}\left(1+{\frac {2}{5}}\left(1+{\frac {3}{7}}\left(1+{\frac {4}{9}}(1+\cdots )\right)\right)\right)$

Newton.

${\frac {1}{\pi }}={\frac {2{\sqrt {2}}}{9801}}\sum _{k=0}^{\infty }{\frac {(4k)!(1103+26390k)}{(k!)^{4}396^{4k}}}$

Ramanujan.

This converges extraordinarily rapidly. Ramanujan's work is the basis for the fastest algorithms used, as of the turn of the millennium, to calculate π.

${\frac {1}{\pi }}=12\sum _{k=0}^{\infty }{\frac {(-1)^{k}(6k)!(13591409+545140134k)}{(3k)!(k!)^{3}640320^{3k+3/2}}}$

David Chudnovsky and Gregory Chudnovsky.

${\pi }=20\arctan {\frac {1}{7}}+8\arctan {\frac {3}{79}}$

Euler.

Miscellaneous formulæ

Using base 60, π can be approximated to eight significant figures as

$3+{\frac {8}{60}}+{\frac {29}{60^{2}}}+{\frac {44}{60^{3}}}$

In addition, the following expressions approximate π

• accurate to 9 digits:

$(63/25)(17+15{\sqrt {5}})/(7+15{\sqrt {5}})$

• accurate to 3 digits:

${\sqrt {2}}+{\sqrt {3}}$

Karl Popper conjectured that Plato knew this expression; that he believed it to be exactly π; and that this is responsible for some of Plato's confidence in the omnicompetence of mathematical geometry — and Plato's repeated discussion of special right triangles that are either isosceles or halves of equilateral triangles.

• The continued fraction representation of π can be used to generate successively better rational approximations, which start off: 22/7, 333/106, 355/113…. These approximations are the best possible rational approximations of π relative to the size of their denominators.

Less accurate approximations

Main article: Indiana Pi Bill

In 1897, an amateur mathematician from Indiana believed that he had discovered a way to square the circle. He proposed a bill to the state legislature to have his discovery made into law. It was passed in the state house of representatives but postponed indefinitely in the state senate thanks to the intervention of a mathematics professor who was present on other business. The bill, which subsequently entered folklore as the Indiana Pi Bill contained several false mathematical claims from which commentators have extracted a number of apparent "values of π" including 3.2, 3.23.., 4, and 9.24....

Memorizing digits

Main article: Piphilology

Ever since computers have calculated π to billions of decimal places, memorizing π has become a hobby for some people. The current unofficial world record is 83,431 decimal places, and was set by a Japanese mental health counsellor named Akira Haraguchi, who is currently 59 years of age.[3] Before Haraguchi accomplished this on July 2, 2005, the world record was 42,195, which was set by Hiroyuki Goto. See here, a website listing many people who have memorized impressive amounts of π.

There are many ways to memorize π, including the use of piems, which are poems that represent π in a way such that the length of each word (in letters) represents a digit. Here is an example of a piem: How I need a drink, alcoholic in nature (or: of course), after the heavy lectures involving quantum mechanics. Notice how the first word has 3 letters, the second word has 1, the third has 4, the fourth has 1, the fifth has 5, and so on. The Cadaeic Cadenza contains the first 3834 digits of π in this matter. Piems are related to the entire field of humorous yet serious study that involves the use of mnemonic techniques to remember the digits of π, known as piphilology. See Pi mnemonics for examples. In other languages there are similar methods of memorization.

Open questions

The most pressing open question about π is whether it is a normal number -- whether any digit block occurs in the expansion of π just as often as one would statistically expect if the digits had been produced completely "randomly", and that this is true in every base, not just base 10. Current knowledge on this point is very weak; e.g., it is not even known which of the digits 0,…,9 occur infinitely often in the decimal expansion of π.

Bailey and Crandall showed in 2000 that the existence of the above mentioned Bailey-Borwein-Plouffe formula and similar formulæ imply that the normality in base 2 of π and various other constants can be reduced to a plausible conjecture of chaos theory. See Bailey's above mentioned web site for details.

It is also unknown whether π and e are algebraically independent. However it is known that at least one of πe and π + e is transcendental (q.v.).

Naturality

In non-Euclidean geometry the sum of the angles of a triangle may be more or less than π radians, and the ratio of a circle's circumference to its diameter may also differ from π. This does not change the definition of π, but it does affect many formulæ in which π appears. So, in particular, π is not affected by the shape of the universe; it is not a physical constant but a mathematical constant defined independently of any physical measurements. Nonetheless, it occurs often in physics.

For example, consider Coulomb's law (SI units)

$F={\frac {1}{4\pi \epsilon _{0}}}{\frac {\left|q_{1}q_{2}\right|}{r^{2}}}$.

Here, 4πr² is just the surface area of sphere of radius r. In this form, it is a convenient way of describing the inverse square relationship of the force at a distance r from a point source. It would of course be possible to describe this law in other, but less convenient ways, or in some cases more convenient. If Planck charge is used, it can be written as

$F={\frac {q_{1}q_{2}}{r^{2}}}$

and thus eliminate the need for π.

Fictional references

• In Carl Sagan's science fiction Contact, Sagan contemplates the possibility of finding a signature embedded in the base-11 expansion of π by the creators of the universe.
• In Greg Bear's science fiction novel Eon, the protagonists measure the amount of space curvature using a device that computes π. Only in completely flat space/time will a circle have a circumference–diameter ratio of 3.14159….
• In Terry Pratchett's fantasy novel Going Postal, the famous inventor Bloody Stupid Johnson invents an organ/mail sorter that contains a wheel for which π is exactly 3. This "New π" starts a chain of events that leads to the failure of the Ankh-Morpork Post Office (and possibly the destruction of the Universe all in one go.)
• In the cult film π, the relationship between numbers and nature is analyzed.
• In the cartoon series The Simpsons, "π is exactly three!" was an announcement used by Professor Frink to gain the full attention of a hall full of scientists.
• The cartoon series Futurama also contains several references to π, such as the use of 'π in 1' oil, and shopping at πkea.
• In the Star Trek episode "Wolf in the Fold", when the computer of the Enterprise is taken over by an evil alien, Spock tells the computer to figure π to the last digit, which forces the alien to leave.
• In the Doctor Who episode "The Five Doctors", the First Doctor uses π in an application to get across a deadly chessboard floor in the Dark Tower of Rassilon, after figuring out the statement made by The Master that the chessboard is; "easy as 'pi'."
• The science fiction novel Time's Eye, by Arthur C. Clarke and Stephen Baxter, depicts a world restructured by alien forces. A spherical device is observed whose circumference-to-diameter ratio appears to be an exact integer 3 across all planes. It is the first book in The Time Odyssey series.
• In the Jimmy Neutron episode "Revenge of the Nanobots," Jimmy destroys the nanobots (which were designed to fix all errors, and were destroying mankind due to an excessively high standard of "error-free") by making them correct a test paper which states that π equals 3.
• The Ragged Astronauts, a science-fiction novel by Bob Shaw, describes 2 planets, Land & Overland, which share atmospheres. π is discovered by the most eminent philosopher of Land to be exactly 3. Subsequent books in the trilogy involve another planet (Farland), and the discovery of changes to the value of π.
• In The Time Warp Trio, Sam shuts down a threatening robot by telling it that his number was π.

Trivia

The circumference of a circle is π times its diameter. A straight line may be marked off in equal measures, each the diameter of a given circle. This may be done legitimately with the classical construction methods of Euclidean geometry, using compass and straightedge. Departing entirely from classical construction, we may mount the given circle on a wheel and roll it along the straight line, unrolling the circumference as we go. The wheel rim is covered with red paint, which is transferred to the road as the wheel travels. As shown by the animation, it travels an unusual, counterintuitive distance before making a full revolution: almost one-seventh again beyond three diameters. This is the number π.

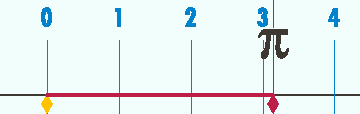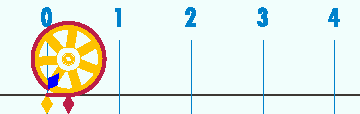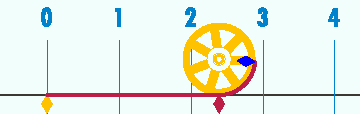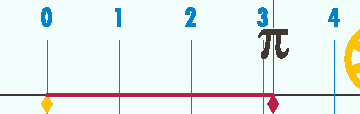
• March 14 (3/14 in U.S. date format) marks Pi Day which is celebrated by many lovers of π. Incidentally, it is also Einstein's birthday.
• On July 22, Pi Approximation Day is celebrated (22/7 - in European date format - is a popular approximation of π).
• 355/113 (~3.1415929) is sometimes jokingly referred to as "not π, but an incredible simulation!"
• Singer Kate Bush's 2005 album "Aerial" contains a song titled "π", in which she sings π to its 137th decimal place; however, for an unknown reason, she omits the 79th to 100th decimal places.[4] She was preceded in this achievement by several years by a Swedish indie math lyrics artist under the moniker Matthew Matics, who loses track of the decimals at about the same point in the series.
• John Harrison (1693–1776) (of Longitude fame), devised a meantone temperament musical tuning system derived from π, now called Lucy Tuning.
• Users of the A9.com search engine are eligible for an amazon.com program offering discounts of (π/2)% on purchases.
• The Heywood Banks song "Eighteen Wheels on a Big Rig" has the singer(s) count pi in the final verse; they reach "eight hundred billion" before going into the chorus.
• In 1932, Stanisław Gołąb proved that the ratio of the circumference to the diameter of the unit disc is always in between 3 and 4; these values are attained if and only if the unit "circle" has the shape of a regular hexagon resp. a parallelogram. See unit disc for details.
• John Squire (of The Stone Roses) mentions π in a song written for his second band The Seahorses called "Something Tells Me". The song was recorded in full by the full band, and appears on the bootleg of the never released second-album recordings. The song ends with the lyrics, "What's the secret of life? It's 3.14159265, yeah yeah!!"
• Hard 'N Phirm's fourth track on Horses and Grasses is "Pi" (and is preceded by "An Intro", which discusses the topic like an educational television program). Many digits are recited through it, and a video appeared online inspired by it. Subsequently, it became a popular YTMND called 3.141592653589793....
• If you approximate pi to the 39th digit, you can calculate the area of a circle the entire known universe with accuracy to the width of 1 hydrogen atom.

See also

• List of topics related to pi
• Greek letter π
• Calculus
• Geometry
• Trigonometric function
• Pi through experiment
• Proof that π is transcendental
• A simple proof that 22/7 exceeds π
• Feynman point
• Pi Day
• Lucy Tuning
• Cadaeic Cadenza
• Software for calculating π on personal computers
• History of π
• History of numerical approximations of π
• Mathematical Constants
  • e
  • φ

References

• Bailey, David H., Borwein, Peter B., and Plouffe, Simon (1997). "On the Rapid Computation of Various Polylogarithmic Constants" (PDF). Mathematics of Computation. 66 (218): 903–913. {{cite journal}}: Unknown parameter |month= ignored (help)CS1 maint: multiple names: authors list (link)

• A new formula to compute the n'th binary digit of pi by Fabrice Bellard, retrieved March 22, 2006

• Petr Beckmann, A History of π

• Jonathan Sondow, "A faster product for pi and a new integral for ln pi/2," Amer. Math. Monthly 112 (2005) 729-734.

• Jonathan Sondow, Problem 88, Math Horizons 5 (Sept., 1997) 32, 34.

External links

Digits

• 4 Million Digits of π
• Project Gutenberg E-Text containing a million digits of π
• Search the first 200 million digits of π for arbitrary strings of numbers
• Source code for calculating the digits of π
• Search π – search and print π's digits (up to 3.2 billion places)
• Pi World ranking list
• million digits of π and other constants in .txt and .zip files
• π available in various lengths, up to 4.2 billion digits
• A million digits of π

General

• J J O'Connor and E F Robertson: A history of pi. Mac Tutor project
• A proof that π Is Irrational
• From the Wolfram Mathematics site lots of formulæ for π
• PlanetMath: Pi
• Finding the value of π
• Determination of π at cut-the-knot
• The Life of Pi by Jonathan Borwein
• BBC Radio Program about π