Mixed-order Ambisonics

Main article: Ambisonics

It is possible to define an Ambisonic signal set with non-uniform resolution, depending on source direction. This practice is called mixed-order, and it has consequences for the layout and interpretation of files, streams, or physical connections in Ambisonic data exchange. As with all things Ambisonic, its complexity has increased as research progressed, and the term has grown to include new different concepts which were not in common use when Ambisonics was first invented in the 1970s.

When dealing with such subsets of the multipole expansion, the base ordering of the components (according to whatever ordering scheme has been agreed on) is usually not changed. Instead, the unused components are simply left out, or, where bandwidth or space is not at a premium, zeroed.

True Mixed-order schemes

Horizontal-only

The Ambisonic components up to third order.

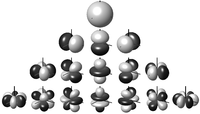
Horizontal-only recordings or mixes are the most commonly encountered mixed-order signals, because the horizontal plane is by far the most likely location of musical or other performers, and the vast majority of playback systems deployed today do not have height capability. Horizontal-only signal sets are derived by following along the edges of the pyramid in the usual depiction of spherical harmonics (see illustration) and taking only the outermost components. Observe how the other componets in each order have either nulls on their equators or lobes with broader expansion than the outer ones, adding no additional resolution information.

Superimposed horizontal and full-sphere signals (#H#P notation)

Often, height localisation is of secondary importance and full-sphere information is only sought for a more pleasant rendering of diffuse room reverberation. Hence, it is customary to take a first-order recording of a tetrahedral microphone and augment it with artificially panned signals in second order, resulting in a 2H1P (or second-order horizontal, first-order periphonic) signal.

If sources are concentrated on the horizontal plane, the result is quite efficient in terms of bandwidth and reproduction complexity. However, an often-overlooked misfeature of such system is that as soon as a source leaves the horizontal plane, its sharpness and area of satisfactory reconstruction degrades rapidly to that of the periphonic order.

Complete mixed-order sets (#H#V)

To address this issue, Travis (2009) suggested an augmented mixed-order scheme which retains its horizontal resolution even for elevated sources, while limiting the lower order "smear" to the vertical dimension. For such sets, the #H#V notation has become common, where H denotes the horizontal resolution and V the vertical, with the understanding that they will be constant for all source positions on the sphere.

1. H#V sets are derived by following the pyramid of spherical harmonics along the edges, taking the #V outermost components of each row on each side. For example, a 3H2V set has 15 components, leaving out only the third-order z-rotationally symmetric one in the middle of the bottom row.

Signals defined for particular subsets of the sphere

Nachbar et al, Zotter, IEM: Hemispheric base functions, signals defined for "windows" on the sphere. Caution: since these use different base functions, they are not mixed-order or even B-format in the traditional sense.